六年级数学下册课件 4.2 正比例 北师大版(共21张PPT)
文档属性
| 名称 | 六年级数学下册课件 4.2 正比例 北师大版(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 15:25:05 | ||
图片预览







文档简介
复习
1.已知路程和时间,怎样求速度?
速度 = 路程÷时间
2.已知总价和数量,怎样求单价?
单价 = 总价÷数量
3.已知工作总量和工作时间,怎样求工作效率?
工作效率 = 工作总量÷工作时间
正 比 例
北师大版六年级数学下册
学习目标
1.理解正比例的意义。
2.会判断两个量是否成正比例的量。
3.体会数学与生活中的联系。
总价: 元
14.38
21.57
7.19
28.76
35.95
43.14
50.33
57.52
64.71
单价:7.19元
合作探究:请认真观察,你的发现了什么?
数量: 本
2
1
5
4
3
7
6
8
9
总价: 元
14.38
21.57
7.19
28.76
35.95
43.14
50.33
57.52
64.71
单价:7.19元
数量: 本
1
2
3
4
5
6
7
8
9
合作探究:请认真观察,你的发现了什么?
1.表中有哪两种相关联的量?
2.说说总价是怎样随数量的变化而变化的呢?
3.相对应的总价和数量的比值各是多少?表示
什么呢?有什么特点?
数量∕本
1
2
3
4
5
6
7
8
9
总价/元
7.19
14.38
21.57
28.76
35.95
43.14
50.33
57.52
64.71
单价/元
7.19
7.19
7.19
7.19
7.19
7.19
7.19
7.19
7.19
小组讨论:
议一议
1.表中有哪两种相关联的量?
总价和数量
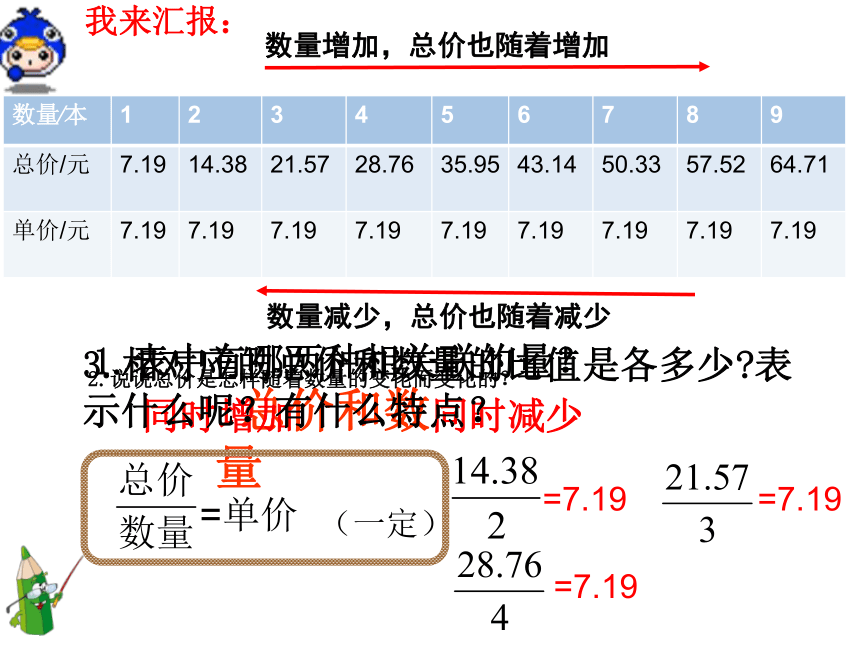
我来汇报:
2.说说总价是怎样随着数量的变化而变化的?
数量增加,总价也随着增加
数量减少,总价也随着减少
同时增加
同时减少
3.相对应的总价和数量的比值是各多少?表示什么呢?有什么特点?
=单价
=7.19
(一定)
=7.19
=7.19
数量∕本
1
2
3
4
5
6
7
8
9
总价/元
7.19
14.38
21.57
28.76
35.95
43.14
50.33
57.52
64.71
单价/元
7.19
7.19
7.19
7.19
7.19
7.19
7.19
7.19
7.19
实验:
认真观察实验,你发现了什么?
底面积/cm
体积/cm
高度/cm
3
100
100
100
100
100
100
1
2
3
4
5
6
100
200
300
400
500
600
2
1.表中有哪两种相关联的量?
体积和高度
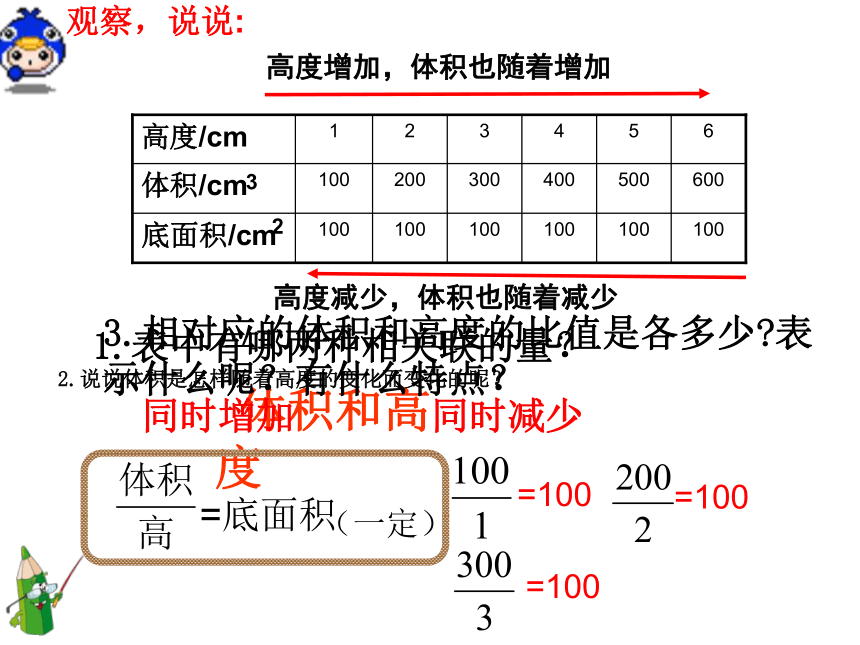
观察,说说:
2.说说体积是怎样随着高度的变化而变化的呢?
高度增加,体积也随着增加
高度减少,体积也随着减少
同时增加
同时减少
3.相对应的体积和高度的比值是各多少?表示什么呢?有什么特点?
=底面积
=100
(一定)
=100
=100
100
100
100
100
100
100
底面积/cm
600
500
400
300
200
100
体积/cm
6
5
4
3
2
1
高度/cm
3
2
(1)都有两种相关联的量。
我们回顾刚才的两道例题,说说它们有什么共同点?
2.水的体积与高度如下表:
(3)相对应的两个量的比值(也就是商)一定。
(2)一种量增加(或减少),另一种量也增加(或减少)。
1.数学书的数量与总价如下表:
比一比:
100
100
100
100
100
100
底面积/cm
600
500
400
300
200
100
体积/cm
6
5
4
3
2
1
高度/cm
3
2
数量∕本
1
2
3
4
5
6
7
8
9
总价/元
7.19
14.38
21.57
28.76
35.95
43.14
50.33
57.52
64.71
单价/元
7.19
7.19
7.19
7.19
7.19
7.19
7.19
7.19
7.19
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
①
②
③
想一想:
判断两种量是否成正比例关系?关键看什么?
(1)都有两种相关联的量。
(2)同时变化。
(3)相对应的两个量的比值
(也就是商)一定。
判断下面各题中两种相关联的量是否成正比例,并说明理由。
1.工作效率一定时,工作总量和工作时间。
2.工作时间一定时,工作总量与工作效率。
答:工作总量和工作时间成正比例。
因为 工作总量÷工作时间=工作效率(一定)。
答:工作总量和工作效率成正比例。
因为 工作总量÷工作效率=工作时间(一定)。
小试牛刀:
边长/cm
1
2
3
周长/cm
4
边长/cm
1
2
3
面积/cm2
1
边长发生变化,周长和面积也发生变化。
正方形的周长和边长成正比例。
正方形的面积和边长不成正比例。
思考:
正方形的周长与边长、面积与边长之间的变化
情况,它们成正比例关系吗?
8
12
16
4
4
9
16
4
我知道:两种( )的量,一种量变化,另一种量也随着( ),如果这两种量中相对应的两个数的( )一定,这两种量就叫做成正比例的量,它们的关系叫做( )。
我的收获
相关联
变化
比值
成正比例关系
智慧城堡
加油啊!
1.判断下面各题中的两种量是否成正比例,
并说明理由。
( 1) 圆的周长与它的直径。
圆的周长与直径是两种相关联的量,而且
所以圆的周长与直径成正比例。
(2)小新跳高的高度和他的身高。
跳高的高度和身高不是两种相关联的量,
所以小新跳高的高度和他的身高不成正比例.
1.判断下面各题中的两种量是否成正比例,
并说明理由。
( 3) 比例尺一定,图上距离与实际距离。
( 4) 和一定,一个加数与另一个加数。
图上距离和实际距离是两种相关联的量,
而且图上距离:实际距离=比例尺(一定)。
所以图上距离与实际距离成正比例。
两个量成正比例是比值一定,不是和一定。
所以一个加数和另一个加数不成正比例。
2.选择。
? 成正比例的两个量在变化时,它们的( )不变。
A.积 B.比值 C.和 D.差
? 下列选项中,( )成正比例。
A.正方形的面积和周长 B.圆的半径和直径
C.和一定的两个数 D.长方形的长和宽
? 当圆柱的( )一定时,圆柱的体积与高成正比例。
A.表面积 B.侧面积 C.底面积
B
B
C
3.乐乐和爸爸的年龄变化情况如下,把表填写完整。
乐乐的年龄/岁
6
7
8
9
10
11
爸爸的年龄/岁
32
33
34
乐乐的年龄与爸爸年龄是两个相关联的两,但是比值不是一个确定的值,
他们的年龄成正比例吗?为什么?
35
36
37
所以,他们的年龄不成正比例。
黄金分割
是指事物各部分间存在的正比例关系,即将整体一分为二,较大部分与较小部分之比等于整体与较大部分之比,其比为1:1.618或0.618:1,即长段为全段的0.618。0.618被公认为最具有审美意义的比例数字,最能引起人的美感的比例,因此被称为黄金分割。在生活中应用比比皆是。
视频
1.已知路程和时间,怎样求速度?
速度 = 路程÷时间
2.已知总价和数量,怎样求单价?
单价 = 总价÷数量
3.已知工作总量和工作时间,怎样求工作效率?
工作效率 = 工作总量÷工作时间
正 比 例
北师大版六年级数学下册
学习目标
1.理解正比例的意义。
2.会判断两个量是否成正比例的量。
3.体会数学与生活中的联系。
总价: 元
14.38
21.57
7.19
28.76
35.95
43.14
50.33
57.52
64.71
单价:7.19元
合作探究:请认真观察,你的发现了什么?
数量: 本
2
1
5
4
3
7
6
8
9
总价: 元
14.38
21.57
7.19
28.76
35.95
43.14
50.33
57.52
64.71
单价:7.19元
数量: 本
1
2
3
4
5
6
7
8
9
合作探究:请认真观察,你的发现了什么?
1.表中有哪两种相关联的量?
2.说说总价是怎样随数量的变化而变化的呢?
3.相对应的总价和数量的比值各是多少?表示
什么呢?有什么特点?
数量∕本
1
2
3
4
5
6
7
8
9
总价/元
7.19
14.38
21.57
28.76
35.95
43.14
50.33
57.52
64.71
单价/元
7.19
7.19
7.19
7.19
7.19
7.19
7.19
7.19
7.19
小组讨论:
议一议
1.表中有哪两种相关联的量?
总价和数量
我来汇报:
2.说说总价是怎样随着数量的变化而变化的?
数量增加,总价也随着增加
数量减少,总价也随着减少
同时增加
同时减少
3.相对应的总价和数量的比值是各多少?表示什么呢?有什么特点?
=单价
=7.19
(一定)
=7.19
=7.19
数量∕本
1
2
3
4
5
6
7
8
9
总价/元
7.19
14.38
21.57
28.76
35.95
43.14
50.33
57.52
64.71
单价/元
7.19
7.19
7.19
7.19
7.19
7.19
7.19
7.19
7.19
实验:
认真观察实验,你发现了什么?
底面积/cm
体积/cm
高度/cm
3
100
100
100
100
100
100
1
2
3
4
5
6
100
200
300
400
500
600
2
1.表中有哪两种相关联的量?
体积和高度
观察,说说:
2.说说体积是怎样随着高度的变化而变化的呢?
高度增加,体积也随着增加
高度减少,体积也随着减少
同时增加
同时减少
3.相对应的体积和高度的比值是各多少?表示什么呢?有什么特点?
=底面积
=100
(一定)
=100
=100
100
100
100
100
100
100
底面积/cm
600
500
400
300
200
100
体积/cm
6
5
4
3
2
1
高度/cm
3
2
(1)都有两种相关联的量。
我们回顾刚才的两道例题,说说它们有什么共同点?
2.水的体积与高度如下表:
(3)相对应的两个量的比值(也就是商)一定。
(2)一种量增加(或减少),另一种量也增加(或减少)。
1.数学书的数量与总价如下表:
比一比:
100
100
100
100
100
100
底面积/cm
600
500
400
300
200
100
体积/cm
6
5
4
3
2
1
高度/cm
3
2
数量∕本
1
2
3
4
5
6
7
8
9
总价/元
7.19
14.38
21.57
28.76
35.95
43.14
50.33
57.52
64.71
单价/元
7.19
7.19
7.19
7.19
7.19
7.19
7.19
7.19
7.19
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
①
②
③
想一想:
判断两种量是否成正比例关系?关键看什么?
(1)都有两种相关联的量。
(2)同时变化。
(3)相对应的两个量的比值
(也就是商)一定。
判断下面各题中两种相关联的量是否成正比例,并说明理由。
1.工作效率一定时,工作总量和工作时间。
2.工作时间一定时,工作总量与工作效率。
答:工作总量和工作时间成正比例。
因为 工作总量÷工作时间=工作效率(一定)。
答:工作总量和工作效率成正比例。
因为 工作总量÷工作效率=工作时间(一定)。
小试牛刀:
边长/cm
1
2
3
周长/cm
4
边长/cm
1
2
3
面积/cm2
1
边长发生变化,周长和面积也发生变化。
正方形的周长和边长成正比例。
正方形的面积和边长不成正比例。
思考:
正方形的周长与边长、面积与边长之间的变化
情况,它们成正比例关系吗?
8
12
16
4
4
9
16
4
我知道:两种( )的量,一种量变化,另一种量也随着( ),如果这两种量中相对应的两个数的( )一定,这两种量就叫做成正比例的量,它们的关系叫做( )。
我的收获
相关联
变化
比值
成正比例关系
智慧城堡
加油啊!
1.判断下面各题中的两种量是否成正比例,
并说明理由。
( 1) 圆的周长与它的直径。
圆的周长与直径是两种相关联的量,而且
所以圆的周长与直径成正比例。
(2)小新跳高的高度和他的身高。
跳高的高度和身高不是两种相关联的量,
所以小新跳高的高度和他的身高不成正比例.
1.判断下面各题中的两种量是否成正比例,
并说明理由。
( 3) 比例尺一定,图上距离与实际距离。
( 4) 和一定,一个加数与另一个加数。
图上距离和实际距离是两种相关联的量,
而且图上距离:实际距离=比例尺(一定)。
所以图上距离与实际距离成正比例。
两个量成正比例是比值一定,不是和一定。
所以一个加数和另一个加数不成正比例。
2.选择。
? 成正比例的两个量在变化时,它们的( )不变。
A.积 B.比值 C.和 D.差
? 下列选项中,( )成正比例。
A.正方形的面积和周长 B.圆的半径和直径
C.和一定的两个数 D.长方形的长和宽
? 当圆柱的( )一定时,圆柱的体积与高成正比例。
A.表面积 B.侧面积 C.底面积
B
B
C
3.乐乐和爸爸的年龄变化情况如下,把表填写完整。
乐乐的年龄/岁
6
7
8
9
10
11
爸爸的年龄/岁
32
33
34
乐乐的年龄与爸爸年龄是两个相关联的两,但是比值不是一个确定的值,
他们的年龄成正比例吗?为什么?
35
36
37
所以,他们的年龄不成正比例。
黄金分割
是指事物各部分间存在的正比例关系,即将整体一分为二,较大部分与较小部分之比等于整体与较大部分之比,其比为1:1.618或0.618:1,即长段为全段的0.618。0.618被公认为最具有审美意义的比例数字,最能引起人的美感的比例,因此被称为黄金分割。在生活中应用比比皆是。
视频
