波粒二象性中不确定关系课件(第五节)
文档属性
| 名称 | 波粒二象性中不确定关系课件(第五节) |

|
|
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2012-01-11 00:00:00 | ||
图片预览









文档简介
(共40张PPT)
17-5.物质波 不确定关系
回顾所学:
1. 物质波是一种什么波
2. 什么是实物粒子的波粒二象性
一. 物质波 实物粒子的波粒二象性
光的干涉、衍射等现象证实了光的波动性;热辐射、光电效应和康普顿效应等现象又证实了光的粒子性。光具有波-粒二象性。
德布罗意波在光的二象性的启发下,提出了与光的二象性完全对称的设想,即实物粒子(如电子、质子等)也具有波-粒二象性的假设。
德布罗意
不仅光具有波粒二象性,一切实物粒子(如电子、原子、分子等)也都具有波粒二象性; 具有确定动量 P 和确定能量 E 的实物粒子相当于频率为 和波长为 的波, 二者之间的关系如同光子和光波的关系一样, 满足:
德布罗意假设:
这种和实物粒子相联系的波称为 德布罗意波 或 物质波 。
例:电子在电场里加速所获得的能量
电子的德布罗意波长
德布罗意公式
X射线范围
玻尔氢原子量子化条件与驻波条件是等效的。
将德布罗意关系式
代入即得
玻尔理论中的角动量量子化条件
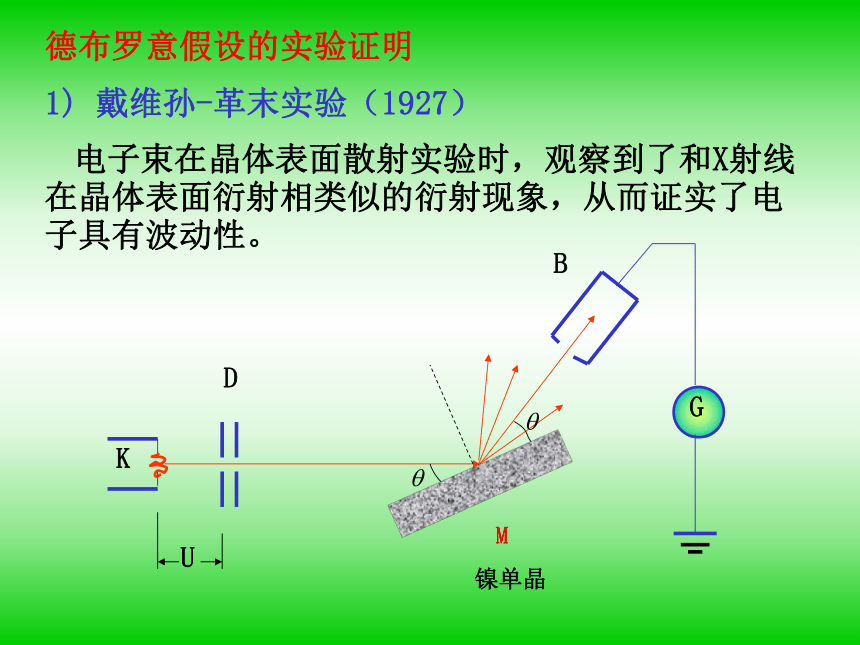
电子束在晶体表面散射实验时,观察到了和X射线在晶体表面衍射相类似的衍射现象,从而证实了电子具有波动性。
K
D
U
M
镍单晶
B
G
1) 戴维孙-革末实验(1927)
德布罗意假设的实验证明
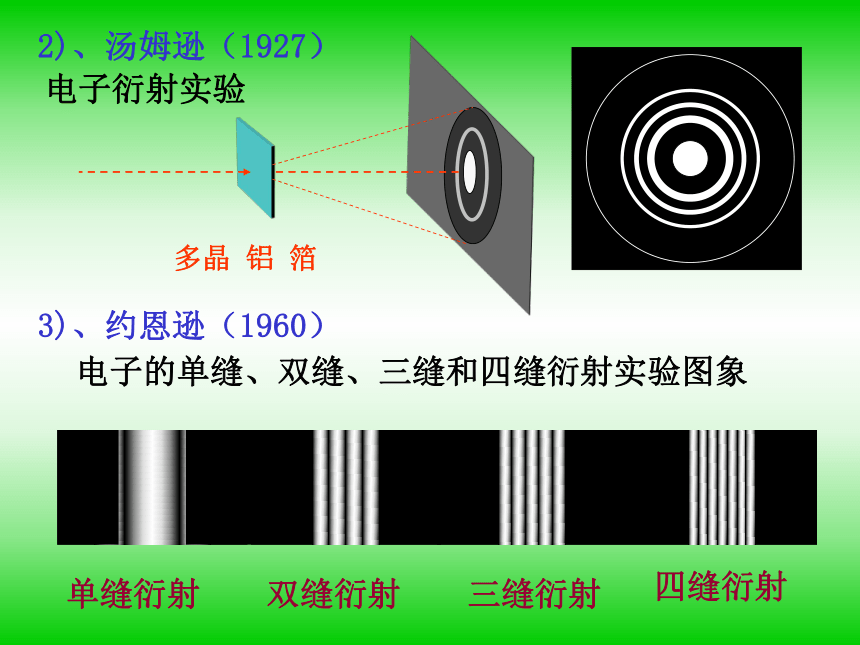
电子衍射实验
多晶 铝 箔
电子的单缝、双缝、三缝和四缝衍射实验图象
2)、汤姆逊(1927)
3)、约恩逊(1960)
单缝衍射
双缝衍射
三缝衍射
四缝衍射
例 计算m=0.01kg,V=300m/s的子弹的德布罗意波长.
极其微小,宏观物体的波长小得实验难以测量,
“宏观物体只表现出粒子性”
因V<波函数及其统计解释
物质波波函数
1926年玻恩指出物质波是一种概率波,它描述了粒子在各处出现的概率。
与经典波用波函数描述类似,如果用一个时间空间函数 描述物质波,则波函数振幅的平方
就表示t时刻,粒子在空间r 处的单位体积中出现的概率,又称为概率密度.
即波函数的物理意义:
—— t 时刻,粒子在空间 r 处的单位体积中出现的概率,又称为概率密度
电子数 N=7
电子数 N=100
电子数 N=3000
电子数 N=20000
电子数 N=70000
单个粒子在哪一处出现是偶然事件;
大量粒子的分布有确定的统计规律。
出现概率小
出现概率大
电子双缝干涉图样
在经典力学中,质点(宏观物体或粒子)在任何时刻都有完全确定的位置、动量、能量等。由于微观粒子具有明显的波动性,以致于它的某些成对物理量(如位置坐标和动量、时间和能量等)不可能同时具有确定的量值。
位置与动量的不确定性关系
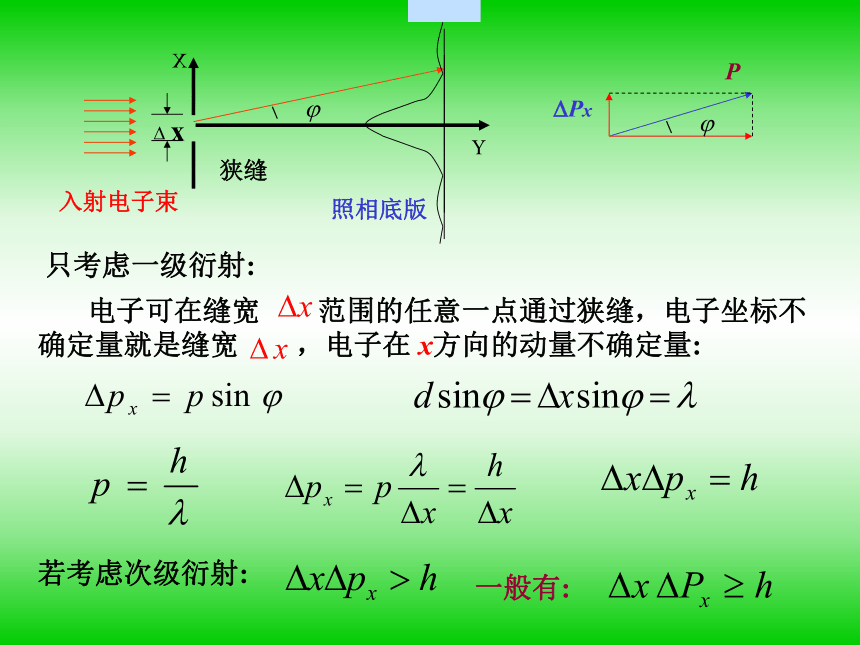
下面以电子单缝衍射为例讨论这个问题
二. 不确定关系
电子可在缝宽 范围的任意一点通过狭缝,电子坐标不确定量就是缝宽 ,电子在 x方向的动量不确定量:
若考虑次级衍射:
只考虑一级衍射:
一般有:
x
入射电子束
狭缝
照相底版
P
Px
严格的理论给出的不确定性关系为:
它的物理意义是,微观粒子不可能同时具有确定的位置和动量。粒子位置的不确定量 越小,动量的不确定量 就越大,反之亦然。因此不可能用某一时刻的位置和动量描述其运动状态。轨道的概念已失去意义,经典力学规律也不再适用。
首先由海森堡给出(1927)
海森堡不确定性关系
(海森堡测不准关系)
----------微观粒子的“波粒二象” 性的具体体现
由于
根据不确定性关系得
解 : 枪口直径可以当作子弹射出枪口时位置的不确定
量 。
和子弹飞行速度每秒几百米相比 ,这速度的不确定性是微不足道的,所以子弹的运动速度是确定的。
例 设子弹的质量为0.01㎏,枪口的直径为0.5㎝。
试求子弹射出枪口时的横向速度的不确定量。
原子线度为10-10m , 计算原子中电子速度的不确定度。
解:
P = m V
例
按经典力学计算,氢原子中电子的轨道速度 V ~106 ms-1 。
物理量与其不确定度一样数量级,物理量没有意义了!
在微观领域内,粒子的轨道概念不适用!
§12—3 波函数 薛定谔方程及简单应用
你知道吗?
1. 物质波波函数的统计意义
2. 一维定态薛定谔方程的物理意义
对于微观粒子,牛顿方程已不适用。
一 一维自由粒子波函数
一个沿 x 轴正向传播的频率为 的平面简谐波:
用指数形式表示:
波的强度
取复数实部
微观粒子的运动状态 描述微观粒子运动基本方程
波函数 薛定谔方程
对于动量为P 、能量为 E 的一维自由微观粒子,根据德布罗意假设,其物质波的波函数相当于单色平面波,类比可写成:
量子力学中一维自由粒子波函数的一般形式
这里的 和 一般都为复数。
波函数的统计意义
亮 波强 电子到达多
暗 波弱 电子到达少
电子双缝衍射
波的强度---------振幅的平方
dV=dx dy dz
单位体积内粒子出现的概率
玻恩(M..Born)的波函数统计解释:
出现在 dV 内概率:
概率密度:
波函数本身无直观物理意义,只有模的平方反映粒子出现的概率,在这一点上不同于机械波,电磁波。
t 时刻粒子出现在空间某点 r 附近体积元 dV 中的概率,与波函数平方及 dV 成正比。
二. 波函数的标准化条件和归一化条件
1、单值: 在一个地方出现只有一种可能性;
2、连续:概率不会在某处发生突变;
3、有限
4、粒子在整个空间出现的总概率等于 1
即:
波函数归一化条件
波函数统计诠释涉及对世界本质的认识争论至今未息
哥本哈根学派
爱因斯坦
波函数满足的条件:单值、有限、连续、归一
三. 薛定谔方程 (1926年)
描述微观粒子在外力场中运动的微分方程 。
质量 m 的粒子在外力场中运动,势能函数 V ( r , t ) ,薛定谔方程为
粒子在稳定力场中运动,势能函数 V ( r ) 、能量 E 不随时间变化,粒子处于定态,定态波函数写为
由上两式得
定态薛定谔方程
粒子能量
(1)求解 E (粒子能量)
( r ) (定态波函数)
(2)势能函数 V 不随时间变化。
一维定态薛定谔方程(粒子在一维空间运动)
描述外力场的势能函数
说明
四.用薛定谔方程解一维无限深势阱
若质量为m的粒子,在保守力场的作用下,被限制在一定的范围内运动,其势函数称为势阱。
为了简化计算,提出理想模型——无限深势阱。
一维无限深势阱:
a
保守力与势能之间的关系:
在势阱边界处,粒子要受到无限大、指向阱内的力,表明粒子不能越出势阱,即粒子在势阱外的概率为0。
势阱内的一维定态薛定谔方程为:
解为:
由边界条件得:
据归一化条件,得
得波函数表达式:
(1)粒子能量不能取连续值
得
能量取分立值(能级),能量量子化是粒子处于束缚态的所具有的性质。
由
讨 论:
(2)粒子的最小能量不等于零
最小能量
也称为基态能或零点能。
零点能的存在与不确定度关系协调一致。
(3)粒子在势阱内出现概率密度分布
不受外力的粒子在0到 a 范围内
出现概率处处相等。
量子论观点:
0
a
=1
=2
=3
=4
n
n
n
n
0
a
当 很大时, 量子概率分布就接近经典分布
经典观点:
(4)有限深势阱,粒子出现的概率分布
如果势阱不是无限深,粒子的能量又低于势璧,粒子在阱外不远处出现的概率不为零。
0
a
经典理论无法解释,实验得到证实。
得到两相邻能级的能量差
例 设想一电子在无限深势阱,如果势阱宽度分别
为1.0×10-2m和10-10m 。试讨论这两中情况下
相邻能级的能量差。
解: 根据势阱中的能量公式
当a=1cm时
可见两相邻能级间的距离随着量子数的增加而增加,而且与粒子的质量m和势阱的宽度a有关。
在这种情况下,相邻能级间的距离是非常小的,我们可以把电子的能级看作是连续的。
当a=10-10m时
在这种情况下,相邻能级间的距离是非常大的,这时电子能量的量子化就明显的表现出来。
可见能级的相对间隔 随着n的增加成反比地减小。当 时 , 较之 要小的多。这时,能量的量子化效应就不显著了,可认为能量是连续的,经典图样和量子图样趋与一致。所以,经典物理可以看作是量子物理中量子数 时的极限情况。
当n>>1 时 ,能级的相对间隔近似为
五.一维方势垒 隧道效应
一维方势阱如图
Ⅰ
Ⅱ
Ⅲ
粒子沿 方向运动,当 粒子可以通过势垒。
当 ,实验证明粒子也能通过势垒,这只有由量子力学得到解释。
设三个区域的波函数分别为
在各区域薛定谔方程分别为
令
为实数
解为:
三个区域中波函数的情况如图所示:
隧道效应
在粒子总能量低于势垒壁高的情况下,粒子有一定的概率穿透势垒. 此现象称为隧道效应。
贯穿势垒的概率定义为在 处透射波的强度与入射波的强度之比:
贯穿概率与势垒的宽度与高度有关。
扫描隧道显微镜(STM)
原理:
利用电子的隧道效应。
金属样品外表面有一层电子云,电子云的密度随着与表面距离的增大呈指数形式衰减,将原子线度的极细的金属探针靠近样品,并在它们之间加上微小的电压,其间就存在隧道电流,隧道电流对针尖与表面的距离及其敏感,如果控制隧道电流保持恒定,针尖的在垂直于样品方向的变化,就反映出样品表面情况。
48个Fe原子形成
“量子围栏”,
围栏中的电子形成驻波。
STM的横向分辨率已达 ,纵向分辨达 ,
STM的出现,使人类第一次能够适时地观察单个原子
在物质表面上的排列状态以及表面电子行为有关性质。
17-5.物质波 不确定关系
回顾所学:
1. 物质波是一种什么波
2. 什么是实物粒子的波粒二象性
一. 物质波 实物粒子的波粒二象性
光的干涉、衍射等现象证实了光的波动性;热辐射、光电效应和康普顿效应等现象又证实了光的粒子性。光具有波-粒二象性。
德布罗意波在光的二象性的启发下,提出了与光的二象性完全对称的设想,即实物粒子(如电子、质子等)也具有波-粒二象性的假设。
德布罗意
不仅光具有波粒二象性,一切实物粒子(如电子、原子、分子等)也都具有波粒二象性; 具有确定动量 P 和确定能量 E 的实物粒子相当于频率为 和波长为 的波, 二者之间的关系如同光子和光波的关系一样, 满足:
德布罗意假设:
这种和实物粒子相联系的波称为 德布罗意波 或 物质波 。
例:电子在电场里加速所获得的能量
电子的德布罗意波长
德布罗意公式
X射线范围
玻尔氢原子量子化条件与驻波条件是等效的。
将德布罗意关系式
代入即得
玻尔理论中的角动量量子化条件
电子束在晶体表面散射实验时,观察到了和X射线在晶体表面衍射相类似的衍射现象,从而证实了电子具有波动性。
K
D
U
M
镍单晶
B
G
1) 戴维孙-革末实验(1927)
德布罗意假设的实验证明
电子衍射实验
多晶 铝 箔
电子的单缝、双缝、三缝和四缝衍射实验图象
2)、汤姆逊(1927)
3)、约恩逊(1960)
单缝衍射
双缝衍射
三缝衍射
四缝衍射
例 计算m=0.01kg,V=300m/s的子弹的德布罗意波长.
极其微小,宏观物体的波长小得实验难以测量,
“宏观物体只表现出粒子性”
因V<
物质波波函数
1926年玻恩指出物质波是一种概率波,它描述了粒子在各处出现的概率。
与经典波用波函数描述类似,如果用一个时间空间函数 描述物质波,则波函数振幅的平方
就表示t时刻,粒子在空间r 处的单位体积中出现的概率,又称为概率密度.
即波函数的物理意义:
—— t 时刻,粒子在空间 r 处的单位体积中出现的概率,又称为概率密度
电子数 N=7
电子数 N=100
电子数 N=3000
电子数 N=20000
电子数 N=70000
单个粒子在哪一处出现是偶然事件;
大量粒子的分布有确定的统计规律。
出现概率小
出现概率大
电子双缝干涉图样
在经典力学中,质点(宏观物体或粒子)在任何时刻都有完全确定的位置、动量、能量等。由于微观粒子具有明显的波动性,以致于它的某些成对物理量(如位置坐标和动量、时间和能量等)不可能同时具有确定的量值。
位置与动量的不确定性关系
下面以电子单缝衍射为例讨论这个问题
二. 不确定关系
电子可在缝宽 范围的任意一点通过狭缝,电子坐标不确定量就是缝宽 ,电子在 x方向的动量不确定量:
若考虑次级衍射:
只考虑一级衍射:
一般有:
x
入射电子束
狭缝
照相底版
P
Px
严格的理论给出的不确定性关系为:
它的物理意义是,微观粒子不可能同时具有确定的位置和动量。粒子位置的不确定量 越小,动量的不确定量 就越大,反之亦然。因此不可能用某一时刻的位置和动量描述其运动状态。轨道的概念已失去意义,经典力学规律也不再适用。
首先由海森堡给出(1927)
海森堡不确定性关系
(海森堡测不准关系)
----------微观粒子的“波粒二象” 性的具体体现
由于
根据不确定性关系得
解 : 枪口直径可以当作子弹射出枪口时位置的不确定
量 。
和子弹飞行速度每秒几百米相比 ,这速度的不确定性是微不足道的,所以子弹的运动速度是确定的。
例 设子弹的质量为0.01㎏,枪口的直径为0.5㎝。
试求子弹射出枪口时的横向速度的不确定量。
原子线度为10-10m , 计算原子中电子速度的不确定度。
解:
P = m V
例
按经典力学计算,氢原子中电子的轨道速度 V ~106 ms-1 。
物理量与其不确定度一样数量级,物理量没有意义了!
在微观领域内,粒子的轨道概念不适用!
§12—3 波函数 薛定谔方程及简单应用
你知道吗?
1. 物质波波函数的统计意义
2. 一维定态薛定谔方程的物理意义
对于微观粒子,牛顿方程已不适用。
一 一维自由粒子波函数
一个沿 x 轴正向传播的频率为 的平面简谐波:
用指数形式表示:
波的强度
取复数实部
微观粒子的运动状态 描述微观粒子运动基本方程
波函数 薛定谔方程
对于动量为P 、能量为 E 的一维自由微观粒子,根据德布罗意假设,其物质波的波函数相当于单色平面波,类比可写成:
量子力学中一维自由粒子波函数的一般形式
这里的 和 一般都为复数。
波函数的统计意义
亮 波强 电子到达多
暗 波弱 电子到达少
电子双缝衍射
波的强度---------振幅的平方
dV=dx dy dz
单位体积内粒子出现的概率
玻恩(M..Born)的波函数统计解释:
出现在 dV 内概率:
概率密度:
波函数本身无直观物理意义,只有模的平方反映粒子出现的概率,在这一点上不同于机械波,电磁波。
t 时刻粒子出现在空间某点 r 附近体积元 dV 中的概率,与波函数平方及 dV 成正比。
二. 波函数的标准化条件和归一化条件
1、单值: 在一个地方出现只有一种可能性;
2、连续:概率不会在某处发生突变;
3、有限
4、粒子在整个空间出现的总概率等于 1
即:
波函数归一化条件
波函数统计诠释涉及对世界本质的认识争论至今未息
哥本哈根学派
爱因斯坦
波函数满足的条件:单值、有限、连续、归一
三. 薛定谔方程 (1926年)
描述微观粒子在外力场中运动的微分方程 。
质量 m 的粒子在外力场中运动,势能函数 V ( r , t ) ,薛定谔方程为
粒子在稳定力场中运动,势能函数 V ( r ) 、能量 E 不随时间变化,粒子处于定态,定态波函数写为
由上两式得
定态薛定谔方程
粒子能量
(1)求解 E (粒子能量)
( r ) (定态波函数)
(2)势能函数 V 不随时间变化。
一维定态薛定谔方程(粒子在一维空间运动)
描述外力场的势能函数
说明
四.用薛定谔方程解一维无限深势阱
若质量为m的粒子,在保守力场的作用下,被限制在一定的范围内运动,其势函数称为势阱。
为了简化计算,提出理想模型——无限深势阱。
一维无限深势阱:
a
保守力与势能之间的关系:
在势阱边界处,粒子要受到无限大、指向阱内的力,表明粒子不能越出势阱,即粒子在势阱外的概率为0。
势阱内的一维定态薛定谔方程为:
解为:
由边界条件得:
据归一化条件,得
得波函数表达式:
(1)粒子能量不能取连续值
得
能量取分立值(能级),能量量子化是粒子处于束缚态的所具有的性质。
由
讨 论:
(2)粒子的最小能量不等于零
最小能量
也称为基态能或零点能。
零点能的存在与不确定度关系协调一致。
(3)粒子在势阱内出现概率密度分布
不受外力的粒子在0到 a 范围内
出现概率处处相等。
量子论观点:
0
a
=1
=2
=3
=4
n
n
n
n
0
a
当 很大时, 量子概率分布就接近经典分布
经典观点:
(4)有限深势阱,粒子出现的概率分布
如果势阱不是无限深,粒子的能量又低于势璧,粒子在阱外不远处出现的概率不为零。
0
a
经典理论无法解释,实验得到证实。
得到两相邻能级的能量差
例 设想一电子在无限深势阱,如果势阱宽度分别
为1.0×10-2m和10-10m 。试讨论这两中情况下
相邻能级的能量差。
解: 根据势阱中的能量公式
当a=1cm时
可见两相邻能级间的距离随着量子数的增加而增加,而且与粒子的质量m和势阱的宽度a有关。
在这种情况下,相邻能级间的距离是非常小的,我们可以把电子的能级看作是连续的。
当a=10-10m时
在这种情况下,相邻能级间的距离是非常大的,这时电子能量的量子化就明显的表现出来。
可见能级的相对间隔 随着n的增加成反比地减小。当 时 , 较之 要小的多。这时,能量的量子化效应就不显著了,可认为能量是连续的,经典图样和量子图样趋与一致。所以,经典物理可以看作是量子物理中量子数 时的极限情况。
当n>>1 时 ,能级的相对间隔近似为
五.一维方势垒 隧道效应
一维方势阱如图
Ⅰ
Ⅱ
Ⅲ
粒子沿 方向运动,当 粒子可以通过势垒。
当 ,实验证明粒子也能通过势垒,这只有由量子力学得到解释。
设三个区域的波函数分别为
在各区域薛定谔方程分别为
令
为实数
解为:
三个区域中波函数的情况如图所示:
隧道效应
在粒子总能量低于势垒壁高的情况下,粒子有一定的概率穿透势垒. 此现象称为隧道效应。
贯穿势垒的概率定义为在 处透射波的强度与入射波的强度之比:
贯穿概率与势垒的宽度与高度有关。
扫描隧道显微镜(STM)
原理:
利用电子的隧道效应。
金属样品外表面有一层电子云,电子云的密度随着与表面距离的增大呈指数形式衰减,将原子线度的极细的金属探针靠近样品,并在它们之间加上微小的电压,其间就存在隧道电流,隧道电流对针尖与表面的距离及其敏感,如果控制隧道电流保持恒定,针尖的在垂直于样品方向的变化,就反映出样品表面情况。
48个Fe原子形成
“量子围栏”,
围栏中的电子形成驻波。
STM的横向分辨率已达 ,纵向分辨达 ,
STM的出现,使人类第一次能够适时地观察单个原子
在物质表面上的排列状态以及表面电子行为有关性质。
