北师大版六年级数学下册 二 比例 第2课时 比例的应用课件(19张ppt)
文档属性
| 名称 | 北师大版六年级数学下册 二 比例 第2课时 比例的应用课件(19张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-12 00:00:00 | ||
图片预览






文档简介
比 例
二
第2课时 比例的应用
北师版数学六年级下册
小兔和小狗赛跑。小兔每分跑100m,小狗每分跑150m。小兔跑了300m时,小猫发现小狗超过小兔很远了。可是,小猫不知道小狗跑了多远。
聪明的你能帮小猫算一算小狗跑了多远吗?
人们有时使用“物物交换”的方式,按一定的比例交换自己所需要的物品。
算一算:14个玩具汽车可以换多少本小人书?
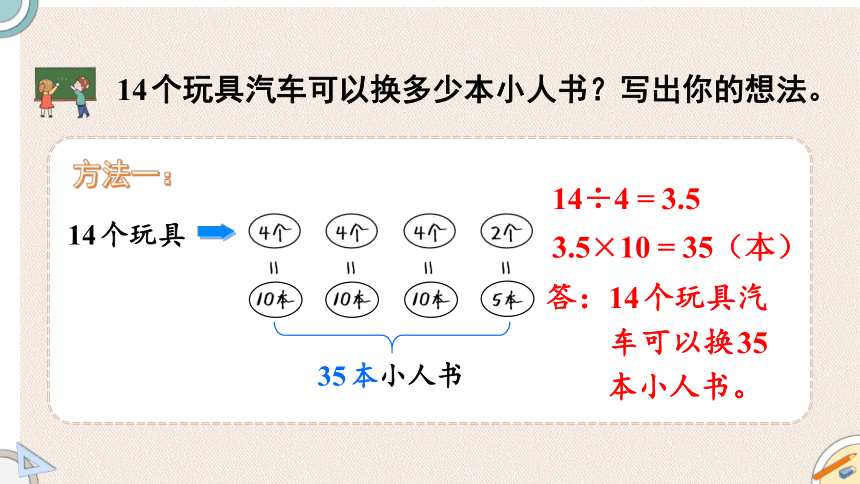
14个玩具汽车可以换多少本小人书?写出你的想法。
14个玩具
35本小人书
14÷4=3.5
3.5×10=35(本)
答:14个玩具汽
车可以换35
本小人书。
14个玩具汽车可以换多少本小人书?写出你的想法。
假设14个玩具汽车可以换x本小人书,尝试用比例的方法解决问题。
4:10=14:x
根据比例的意义可以列出比例。
解:
4x=140
x=35
答:14个玩具汽车可以换35本小人书。
在实际问题中,当已知两个量的比或两个量的比不变时,可以设要求的一个量为x,然后根据比例的意义列出比例,再求出x的值。
解下面的比例,与同伴交流。
24:0.3=x:0.4
24:0.3=x:0.4
解下面的比例,与同伴交流。
24:0.3=x:0.4
24:0.3=x:0.4
解:
0.3x=0.4×24
x=9.6÷0.3
x=32
把求出的结果带入比例验算一下看等式是否成立。
验算:
24:0.3=32:0.4=80:1
解下面的比例,与同伴交流。
24:0.3=x:0.4
解:
7x=4×3.5
x=14÷7
x=2
把求出的结果带入比例验算一下看等式是否成立。
验算:
果园里有梨树80棵,苹果树与梨树的比是5:4,苹果树有多少棵?
1
解:设苹果树有x棵。
x:80=5:4
4x=5×80
x=400÷4
x=100
答:苹果树有100棵。
博物馆展出了一个高为19.6cm的秦代将军俑模型,它的高度与实际高度的比是1:10。这个将军俑的实际高度是多少米?
2
解:设这个将军俑的实际高度是x厘米。
x=10×19.6
x=196
196cm=1.96m
答:这个将军俑实际高度是1.96米。
作业本上的6个小星星可以换2面小红旗。淘气的作业本上已经有了15个小星星。假设15个小星星可以换x面小红旗,你能列比例并解决问题吗?
3
6:2=15:x
解:
6x=15×2
x=30÷6
x=5
解方程式。
4
4:9=x:3.6
4:9=x:3.6
解:
9x=3.6×4
x=14.4÷9
x=1.6
解:
27x=18×9
x=162÷27
x=6
解:
广州塔高600m,是目前世界第一高的电视塔。星星公司设计制作了这座电视塔的模型,模型的高度与实际高度的比是1:300。模型的高度是多少米?
5
解:设模型的高度是x米。
x:600=1:300
300x=1×600
x=600÷300
x=2
答:模型的高度是2米。
淘气和笑笑收集的邮票张数的比是3:5。淘气收集了36张邮票,笑笑收集的邮票有多少张?
6
解:设笑笑收集的邮票有x张。
36:x=3:5
3x=5×36
x=180÷3
x=60
答:笑笑收集的邮票有60张。
甲、乙两家公司合作一项工程,经共同协商,获利将按投资的比进行分配,甲公司投了100万元,乙公司投了80万元,该工程的第一期完工后获利7.2万元。那么分利时,甲公司获利多少万元?乙公司呢?
能力点:用比例的知识解决分配问题。
解:设甲公司在第一期工程获利x万元,
则乙公司为(7.2?x)万元。
100:80=x:(7.2?x)
80x=100(7.2?x)
80x=720?100x
x=4
7.2?4=3.2(万元)
答:甲公司获利4万元,
乙公司获利3.2万元。
1. 根据比例的基本性质,将比例转化成乘积式(等积式),然后求比例中的未知数x的过程叫作解比例。
2. 对于一些具体的实际问题可以列算式求解,也可以根据比例的意义,列出比例(方程),然后解比例,求出实际问题的答案,其关键是理解题意,正确地列出比例。
知识点:解比例
课后作业
1. 填空题。
2. 解比例。
4:11=x:99
3. 笑笑和乐乐两人收集的故事书本比是4:7,乐乐收集了63本故事书,
笑笑收集了多少本故事书?
4. 修一条总长12km的公路,开工3天修了1.5km。照这样的速度,
修完这条公路还要多少天?
二
第2课时 比例的应用
北师版数学六年级下册
小兔和小狗赛跑。小兔每分跑100m,小狗每分跑150m。小兔跑了300m时,小猫发现小狗超过小兔很远了。可是,小猫不知道小狗跑了多远。
聪明的你能帮小猫算一算小狗跑了多远吗?
人们有时使用“物物交换”的方式,按一定的比例交换自己所需要的物品。
算一算:14个玩具汽车可以换多少本小人书?
14个玩具汽车可以换多少本小人书?写出你的想法。
14个玩具
35本小人书
14÷4=3.5
3.5×10=35(本)
答:14个玩具汽
车可以换35
本小人书。
14个玩具汽车可以换多少本小人书?写出你的想法。
假设14个玩具汽车可以换x本小人书,尝试用比例的方法解决问题。
4:10=14:x
根据比例的意义可以列出比例。
解:
4x=140
x=35
答:14个玩具汽车可以换35本小人书。
在实际问题中,当已知两个量的比或两个量的比不变时,可以设要求的一个量为x,然后根据比例的意义列出比例,再求出x的值。
解下面的比例,与同伴交流。
24:0.3=x:0.4
24:0.3=x:0.4
解下面的比例,与同伴交流。
24:0.3=x:0.4
24:0.3=x:0.4
解:
0.3x=0.4×24
x=9.6÷0.3
x=32
把求出的结果带入比例验算一下看等式是否成立。
验算:
24:0.3=32:0.4=80:1
解下面的比例,与同伴交流。
24:0.3=x:0.4
解:
7x=4×3.5
x=14÷7
x=2
把求出的结果带入比例验算一下看等式是否成立。
验算:
果园里有梨树80棵,苹果树与梨树的比是5:4,苹果树有多少棵?
1
解:设苹果树有x棵。
x:80=5:4
4x=5×80
x=400÷4
x=100
答:苹果树有100棵。
博物馆展出了一个高为19.6cm的秦代将军俑模型,它的高度与实际高度的比是1:10。这个将军俑的实际高度是多少米?
2
解:设这个将军俑的实际高度是x厘米。
x=10×19.6
x=196
196cm=1.96m
答:这个将军俑实际高度是1.96米。
作业本上的6个小星星可以换2面小红旗。淘气的作业本上已经有了15个小星星。假设15个小星星可以换x面小红旗,你能列比例并解决问题吗?
3
6:2=15:x
解:
6x=15×2
x=30÷6
x=5
解方程式。
4
4:9=x:3.6
4:9=x:3.6
解:
9x=3.6×4
x=14.4÷9
x=1.6
解:
27x=18×9
x=162÷27
x=6
解:
广州塔高600m,是目前世界第一高的电视塔。星星公司设计制作了这座电视塔的模型,模型的高度与实际高度的比是1:300。模型的高度是多少米?
5
解:设模型的高度是x米。
x:600=1:300
300x=1×600
x=600÷300
x=2
答:模型的高度是2米。
淘气和笑笑收集的邮票张数的比是3:5。淘气收集了36张邮票,笑笑收集的邮票有多少张?
6
解:设笑笑收集的邮票有x张。
36:x=3:5
3x=5×36
x=180÷3
x=60
答:笑笑收集的邮票有60张。
甲、乙两家公司合作一项工程,经共同协商,获利将按投资的比进行分配,甲公司投了100万元,乙公司投了80万元,该工程的第一期完工后获利7.2万元。那么分利时,甲公司获利多少万元?乙公司呢?
能力点:用比例的知识解决分配问题。
解:设甲公司在第一期工程获利x万元,
则乙公司为(7.2?x)万元。
100:80=x:(7.2?x)
80x=100(7.2?x)
80x=720?100x
x=4
7.2?4=3.2(万元)
答:甲公司获利4万元,
乙公司获利3.2万元。
1. 根据比例的基本性质,将比例转化成乘积式(等积式),然后求比例中的未知数x的过程叫作解比例。
2. 对于一些具体的实际问题可以列算式求解,也可以根据比例的意义,列出比例(方程),然后解比例,求出实际问题的答案,其关键是理解题意,正确地列出比例。
知识点:解比例
课后作业
1. 填空题。
2. 解比例。
4:11=x:99
3. 笑笑和乐乐两人收集的故事书本比是4:7,乐乐收集了63本故事书,
笑笑收集了多少本故事书?
4. 修一条总长12km的公路,开工3天修了1.5km。照这样的速度,
修完这条公路还要多少天?
