北师大版六年级数学下册 四 正比例和反比例 第1课时 变化的量课件(18张ppt)
文档属性
| 名称 | 北师大版六年级数学下册 四 正比例和反比例 第1课时 变化的量课件(18张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-13 00:00:00 | ||
图片预览

文档简介
正比例与反比例
四
第1课时 变化的量
北师版数学六年级下册
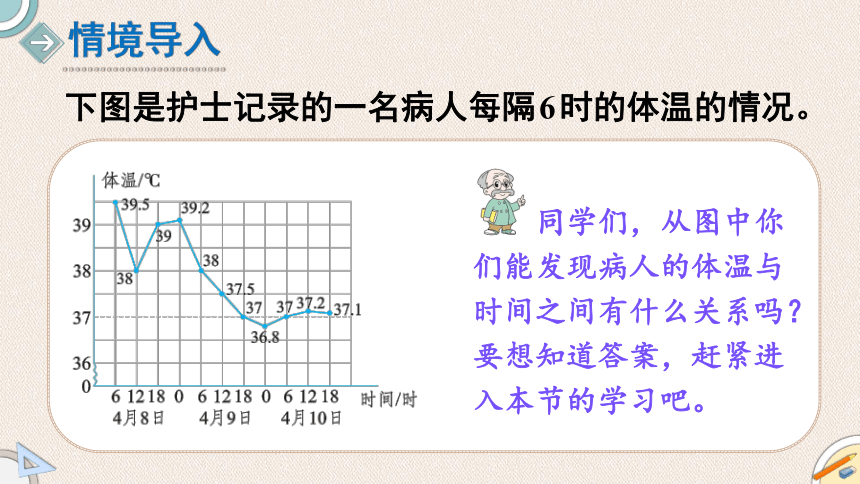
下图是护士记录的一名病人每隔6时的体温的情况。
同学们,从图中你们能发现病人的体温与时间之间有什么关系吗?要想知道答案,赶紧进入本节的学习吧。
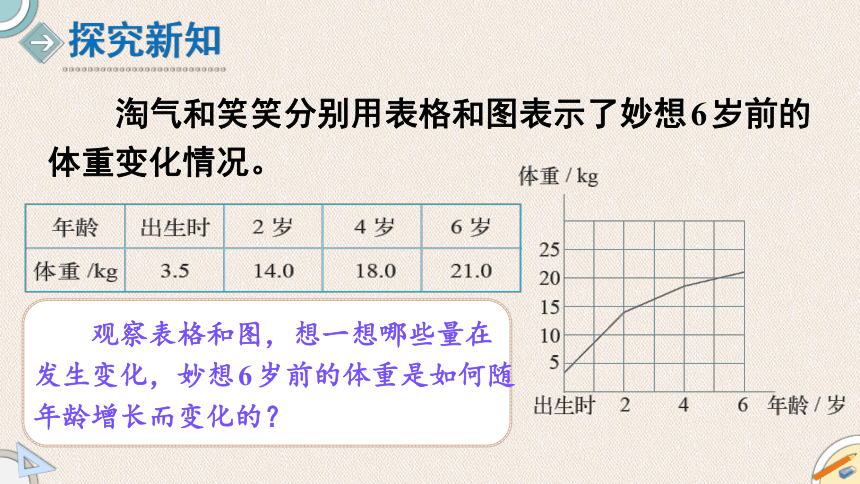
淘气和笑笑分别用表格和图表示了妙想6岁前的体重变化情况。
观察表格和图,想一想哪些量在发生变化,妙想6岁前的体重是如何随年龄增长而变化的?
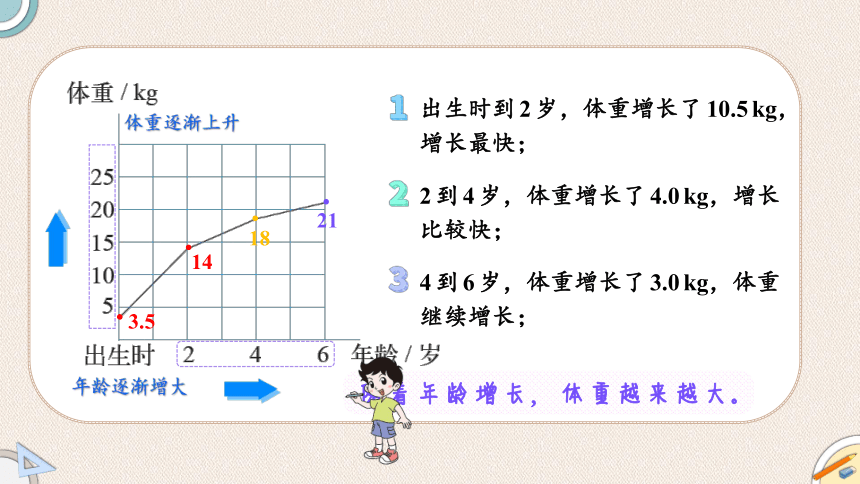
体重逐渐上升
年龄逐渐增大
出生时到2岁,体重增长了10.5kg,增长最快;
2到4岁,体重增长了4.0kg,增长比较快;
4到6岁,体重增长了3.0kg,体重继续增长;
3.5
14
18
21
随着年龄增长,体重越来越大。
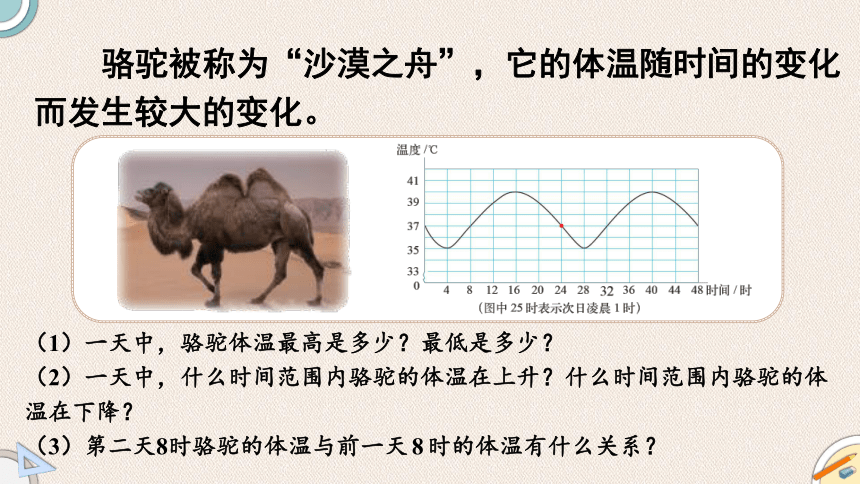
骆驼被称为“沙漠之舟”,它的体温随时间的变化而发生较大的变化。
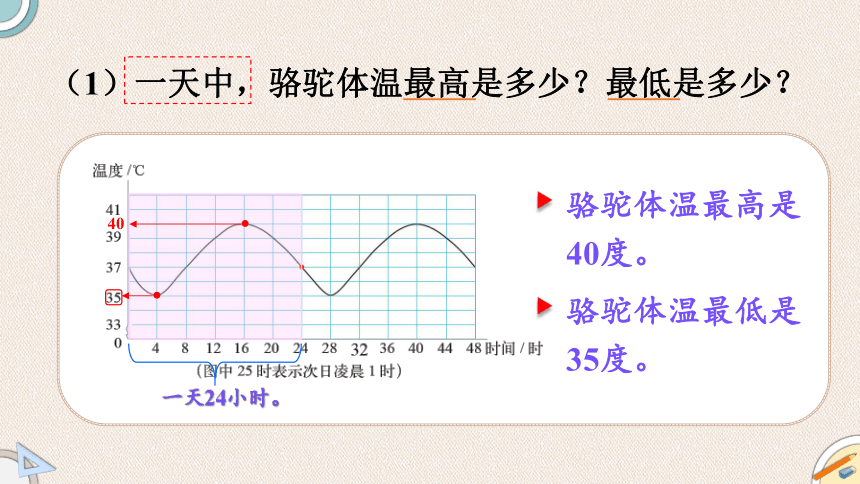
(1)一天中,骆驼体温最高是多少?最低是多少?
(2)一天中,什么时间范围内骆驼的体温在上升?什么时间范围内骆驼的体温在下降?
(3)第二天8时骆驼的体温与前一天8时的体温有什么关系?
(1)一天中,骆驼体温最高是多少?最低是多少?
一天24小时。
骆驼体温最高是40度。
40
骆驼体温最低是35度。
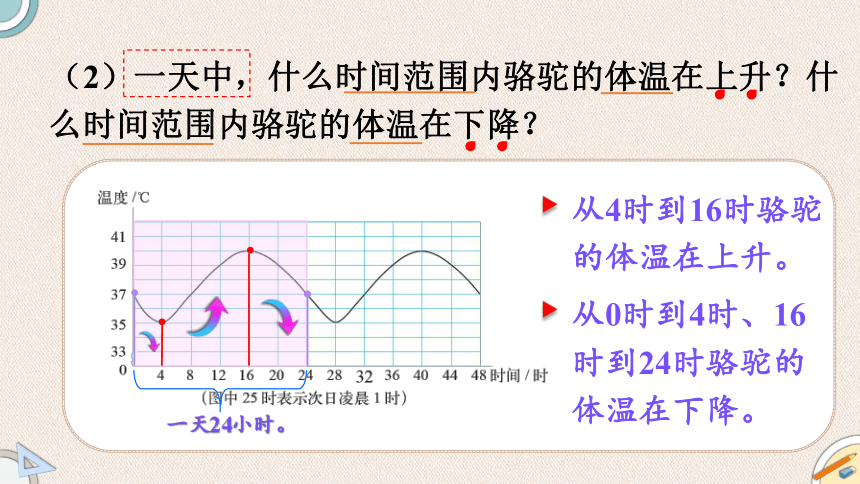
(2)一天中,什么时间范围内骆驼的体温在上升?什么时间范围内骆驼的体温在下降?
一天24小时。
从4时到16时骆驼的体温在上升。
从0时到4时、16时到24时骆驼的体温在下降。
(3)第二天8时骆驼的体温与前一天8时的体温有什么关系?
第二天8时与前一天8时相比,第二天8时的骆驼的体温与前一天8时的体温相同。
当圆柱的底面积等于10cm2时,圆柱的体积和高的变化情况如下表。
结合上表的数据,说一说圆柱的体积与高之间的变化关系。
由表中数据可得,当圆柱的底面积等于10cm?,即底面积一定时,圆柱的体积随高的变化而变化。当高增加时,体积就增加;反之,当高减少时,体积就减少。
2. 你见过摩天轮吗?人所在座舱的高度的变化情况可以
用下图来表示。
(1)转动过程中,到达的最高点是多少米?最低点是多少米?
(2)转动第一圈的过程中,什么时间范围内高度在增加?什么时间范围内高度在降低?
(3)到达最高点后,下一次再到达最高点需要经过几分?
答:(1)最高点是18米,最低点是3米。
(2)转动第一圈的过程中,从0分到6分高度在
增加,从6分到12分高度在降低。
(3)需要经过12分。
3. 某地的一位学生发现蟋蟀叫的次数与气温之间有
如下的近似关系。
t= +3
例:瓶子或罐头盒等物体常如右图那样堆放。若用x表示堆放的层数,y表示堆放罐头盒的总个数,你能用式子表示出y与x的关系吗?
例:瓶子或罐头盒等物体常如右图那样堆放。若用x表示堆放的层数,y表示堆放罐头盒的总个数,你能用式子表示出y与x的关系吗?
一
变化的量:
生活中存在着大量互相依赖的量,如:速度、时间和路程;单价、数量和总价;工作效率、工作时间和工作总量……当其中某一个量发生变化时,另外一个量也会随之变化,这样的两个变量就叫作相关联的量。
课后作业
四
第1课时 变化的量
北师版数学六年级下册
下图是护士记录的一名病人每隔6时的体温的情况。
同学们,从图中你们能发现病人的体温与时间之间有什么关系吗?要想知道答案,赶紧进入本节的学习吧。
淘气和笑笑分别用表格和图表示了妙想6岁前的体重变化情况。
观察表格和图,想一想哪些量在发生变化,妙想6岁前的体重是如何随年龄增长而变化的?
体重逐渐上升
年龄逐渐增大
出生时到2岁,体重增长了10.5kg,增长最快;
2到4岁,体重增长了4.0kg,增长比较快;
4到6岁,体重增长了3.0kg,体重继续增长;
3.5
14
18
21
随着年龄增长,体重越来越大。
骆驼被称为“沙漠之舟”,它的体温随时间的变化而发生较大的变化。
(1)一天中,骆驼体温最高是多少?最低是多少?
(2)一天中,什么时间范围内骆驼的体温在上升?什么时间范围内骆驼的体温在下降?
(3)第二天8时骆驼的体温与前一天8时的体温有什么关系?
(1)一天中,骆驼体温最高是多少?最低是多少?
一天24小时。
骆驼体温最高是40度。
40
骆驼体温最低是35度。
(2)一天中,什么时间范围内骆驼的体温在上升?什么时间范围内骆驼的体温在下降?
一天24小时。
从4时到16时骆驼的体温在上升。
从0时到4时、16时到24时骆驼的体温在下降。
(3)第二天8时骆驼的体温与前一天8时的体温有什么关系?
第二天8时与前一天8时相比,第二天8时的骆驼的体温与前一天8时的体温相同。
当圆柱的底面积等于10cm2时,圆柱的体积和高的变化情况如下表。
结合上表的数据,说一说圆柱的体积与高之间的变化关系。
由表中数据可得,当圆柱的底面积等于10cm?,即底面积一定时,圆柱的体积随高的变化而变化。当高增加时,体积就增加;反之,当高减少时,体积就减少。
2. 你见过摩天轮吗?人所在座舱的高度的变化情况可以
用下图来表示。
(1)转动过程中,到达的最高点是多少米?最低点是多少米?
(2)转动第一圈的过程中,什么时间范围内高度在增加?什么时间范围内高度在降低?
(3)到达最高点后,下一次再到达最高点需要经过几分?
答:(1)最高点是18米,最低点是3米。
(2)转动第一圈的过程中,从0分到6分高度在
增加,从6分到12分高度在降低。
(3)需要经过12分。
3. 某地的一位学生发现蟋蟀叫的次数与气温之间有
如下的近似关系。
t= +3
例:瓶子或罐头盒等物体常如右图那样堆放。若用x表示堆放的层数,y表示堆放罐头盒的总个数,你能用式子表示出y与x的关系吗?
例:瓶子或罐头盒等物体常如右图那样堆放。若用x表示堆放的层数,y表示堆放罐头盒的总个数,你能用式子表示出y与x的关系吗?
一
变化的量:
生活中存在着大量互相依赖的量,如:速度、时间和路程;单价、数量和总价;工作效率、工作时间和工作总量……当其中某一个量发生变化时,另外一个量也会随之变化,这样的两个变量就叫作相关联的量。
课后作业
