垂直于弦的直径
图片预览




文档简介
(共20张PPT)
24.1.2垂直于弦的直径
人教版 九年级上册
教学程序
设疑激趣,导入新课
问题 :你知道赵州桥吗 它是1300多年前我国隋代建造的石拱桥, 是我国古代人民勤劳与智慧的结晶.它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m,你能求出赵洲桥主桥拱的半径吗?
赵州桥主桥拱的半径是多少?
教学程序
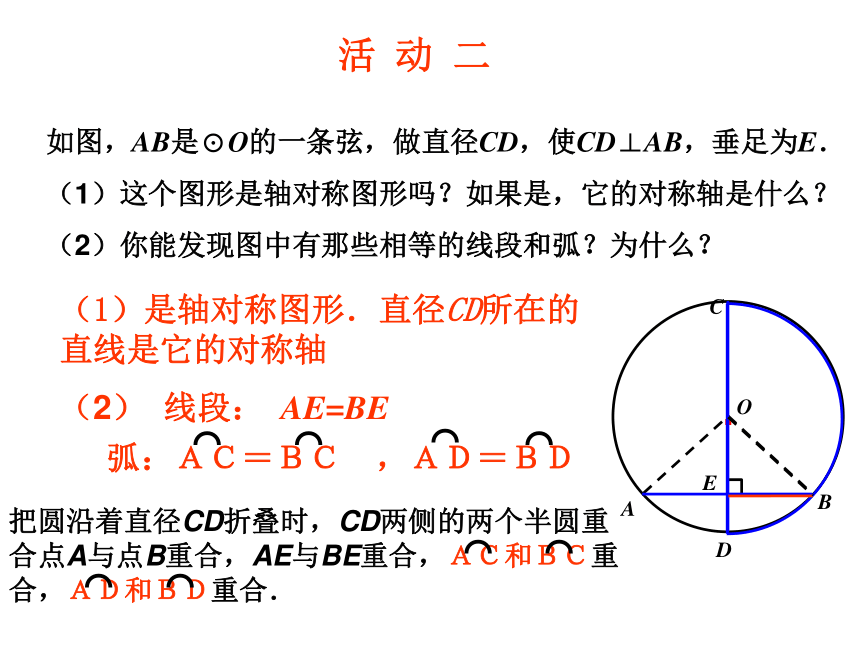
如图,AB是⊙O的一条弦,做直径CD,使CD⊥AB,垂足为E.
(1)这个图形是轴对称图形吗?如果是,它的对称轴是什么?
(2)你能发现图中有那些相等的线段和弧?为什么?
·
O
A
B
C
D
E
活 动 二
(1)是轴对称图形.直径CD所在的直线是它的对称轴
(2) 线段: AE=BE
⌒
⌒
弧:AC=BC ,AD=BD
⌒
⌒
把圆沿着直径CD折叠时,CD两侧的两个半圆重合点A与点B重合,AE与BE重合,AC和BC重合,AD和BD重合.
⌒
⌒
⌒
⌒
·
A
B
C
D
O
P
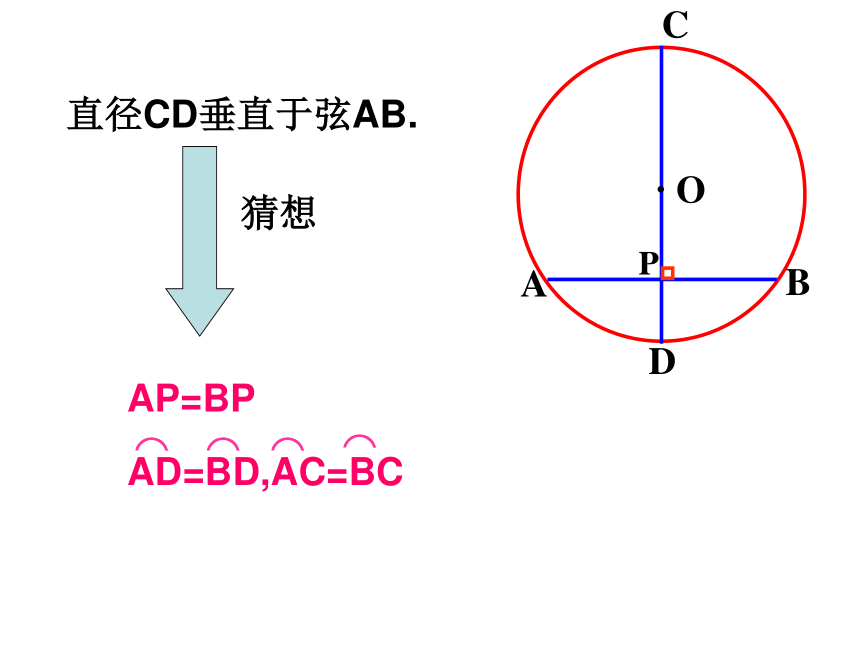
直径CD垂直于弦AB.
猜想
AD=BD,AC=BC
⌒
⌒
⌒
⌒
AP=BP
·
A
B
C
D
O
P
AP = BP,
AC = BC ,AD = BD
⌒
⌒
⌒
⌒
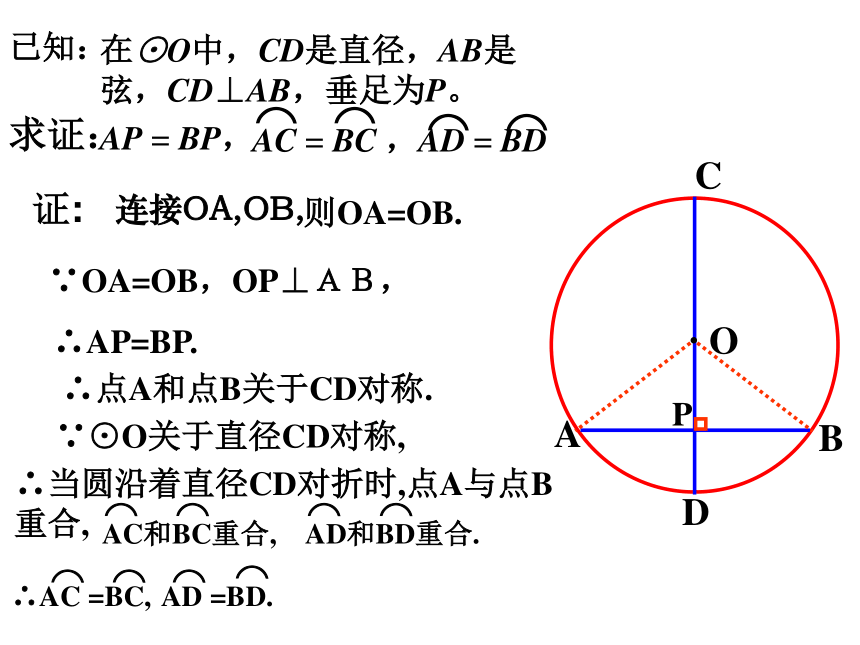
求证:
在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为P。
已知:
连接OA,OB,
则OA=OB.
∵OA=OB,OP⊥AB,
∴AP=BP.
∴点A和点B关于CD对称.
∵⊙O关于直径CD对称,
∴当圆沿着直径CD对折时,点A与点B重合,
⌒
⌒
AC和BC重合,
⌒
⌒
AD和BD重合.
⌒
⌒
∴AC =BC,
⌒
⌒
AD =BD.
证:
教学程序
自己动手,探索新知
教学程序
垂径定理:
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
①过圆心
②垂直于弦
③平分弦
⑤平分弦所对的劣弧
④平分弦所对的优弧
③AP=BP,
由 ① CD是直径
② CD⊥AB
可推得
⌒
⌒
⑤AD=BD.
⌒
⌒
④AC=BC,
垂径定理:
·
A
C
D
O
P
B
教学程序
教学程序
垂径定理的推论:
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
·
O
A
B
C
D
E
②CD⊥AB,
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
由 ① CD是直径
③ AE=BE
可推得
判断下列说法的正误
①平分弧的直径必平分弧所对的弦( )
②平分弦的直线必垂直弦 ( )
③垂直于弦的直径平分这条弦( )
④平分弦的直径垂直于这条弦( )
⑤弦的垂直平分线是圆的直径 ( )
⑥平分弦所对的一条弧的直径必垂直这条弦( )
⑦在圆中,如果一条直线经过圆心且平分弦,
必平分此弦所对的弧 ( )
例1 如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离(弦心距)为3厘米,求⊙O的半径。
.
A
E
B
O
求圆中有关线段的长度时,常借助垂径定理转化为直角三角形,从而利用勾股定理来解决问题.
变式一:在⊙O中,直径为10cm,弦AB的长为8cm,求圆心O 到AB的距离.
变式二:在⊙O中,直径为10cm,圆心O 到AB的距离为3cm,求弦AB的长.
思考:若圆心到弦的距离用d表示,半径用r表示,弦长用a表示,这三者之间有怎样的关系
R
D
B
O
A
C
在图中
在 中,由勾股定理,得
解得:
即
∴赵州桥的主桥拱半径约为 .
教学程序
B
A
如图,用 AB 表示主桥拱,设 AB所在圆的圆心为O,半径为R.经过圆心O 作弦AB 的垂线OC,D为垂足,OC与AB 相交于点D,根据前面的结论,D 是AB 的中点,C是AB 的中点,CD 就是拱高.
⌒
⌒
⌒
解:
2.如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,求证四边形ADOE是正方形.
D
·
O
A
B
C
E
证明:
∴四边形ADOE为矩形,
又 ∵AC=AB
∴ AE=AD
∴ 四边形ADOE为正方形.
教学程序
合作交流,归纳总结
① 本节课的过程、方法、内容是什么?
② 在圆中解决与弦有关问题时,经常做的辅助线是什么?
教学程序
1、必做题:教材87页练习1,2
2、选做题:古人常将玉璜(huáng)悬挂于胸前.你能利用所学的结论,帮助考古学家确定这个璜的
佩戴绳孔的位置吗?
(提示:绳孔在璜的中间
偏上位置.)
耐心填一填:
如图1,在圆O中,若MN⊥AB,MN为直径, 则_________, ____________, ___________.
·
M
O
A
B
N
C
2. 如图2,已知圆O的半径OA长为5,直径MN垂直于AB,AB长为8, 则OC的长为( )
A. 3 B. 6 C. 9 D. 10
3. 如图2:MN为圆O的直径,AB为弦,MN垂直于AB于 点C,则下列结论错误的是( )
A. ∠AOC=∠ BOC B.AC=BC C.MC=NC D.AN=BN
4、圆的半径为3,则弦长x的取值范围是__________.
5、若圆心到该圆的两条平行弦的距离分别是3和5,则此二条平行弦之间的距离是______________.
AC=BC
A
C
⌒
⌒
AN=BN
⌒
⌒
AM=BM
⌒
⌒
0<x≤6
2或8
·
M
N
O
A
B
图2
图1
C
24.1.2垂直于弦的直径
人教版 九年级上册
教学程序
设疑激趣,导入新课
问题 :你知道赵州桥吗 它是1300多年前我国隋代建造的石拱桥, 是我国古代人民勤劳与智慧的结晶.它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m,你能求出赵洲桥主桥拱的半径吗?
赵州桥主桥拱的半径是多少?
教学程序
如图,AB是⊙O的一条弦,做直径CD,使CD⊥AB,垂足为E.
(1)这个图形是轴对称图形吗?如果是,它的对称轴是什么?
(2)你能发现图中有那些相等的线段和弧?为什么?
·
O
A
B
C
D
E
活 动 二
(1)是轴对称图形.直径CD所在的直线是它的对称轴
(2) 线段: AE=BE
⌒
⌒
弧:AC=BC ,AD=BD
⌒
⌒
把圆沿着直径CD折叠时,CD两侧的两个半圆重合点A与点B重合,AE与BE重合,AC和BC重合,AD和BD重合.
⌒
⌒
⌒
⌒
·
A
B
C
D
O
P
直径CD垂直于弦AB.
猜想
AD=BD,AC=BC
⌒
⌒
⌒
⌒
AP=BP
·
A
B
C
D
O
P
AP = BP,
AC = BC ,AD = BD
⌒
⌒
⌒
⌒
求证:
在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为P。
已知:
连接OA,OB,
则OA=OB.
∵OA=OB,OP⊥AB,
∴AP=BP.
∴点A和点B关于CD对称.
∵⊙O关于直径CD对称,
∴当圆沿着直径CD对折时,点A与点B重合,
⌒
⌒
AC和BC重合,
⌒
⌒
AD和BD重合.
⌒
⌒
∴AC =BC,
⌒
⌒
AD =BD.
证:
教学程序
自己动手,探索新知
教学程序
垂径定理:
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
①过圆心
②垂直于弦
③平分弦
⑤平分弦所对的劣弧
④平分弦所对的优弧
③AP=BP,
由 ① CD是直径
② CD⊥AB
可推得
⌒
⌒
⑤AD=BD.
⌒
⌒
④AC=BC,
垂径定理:
·
A
C
D
O
P
B
教学程序
教学程序
垂径定理的推论:
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
·
O
A
B
C
D
E
②CD⊥AB,
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
由 ① CD是直径
③ AE=BE
可推得
判断下列说法的正误
①平分弧的直径必平分弧所对的弦( )
②平分弦的直线必垂直弦 ( )
③垂直于弦的直径平分这条弦( )
④平分弦的直径垂直于这条弦( )
⑤弦的垂直平分线是圆的直径 ( )
⑥平分弦所对的一条弧的直径必垂直这条弦( )
⑦在圆中,如果一条直线经过圆心且平分弦,
必平分此弦所对的弧 ( )
例1 如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离(弦心距)为3厘米,求⊙O的半径。
.
A
E
B
O
求圆中有关线段的长度时,常借助垂径定理转化为直角三角形,从而利用勾股定理来解决问题.
变式一:在⊙O中,直径为10cm,弦AB的长为8cm,求圆心O 到AB的距离.
变式二:在⊙O中,直径为10cm,圆心O 到AB的距离为3cm,求弦AB的长.
思考:若圆心到弦的距离用d表示,半径用r表示,弦长用a表示,这三者之间有怎样的关系
R
D
B
O
A
C
在图中
在 中,由勾股定理,得
解得:
即
∴赵州桥的主桥拱半径约为 .
教学程序
B
A
如图,用 AB 表示主桥拱,设 AB所在圆的圆心为O,半径为R.经过圆心O 作弦AB 的垂线OC,D为垂足,OC与AB 相交于点D,根据前面的结论,D 是AB 的中点,C是AB 的中点,CD 就是拱高.
⌒
⌒
⌒
解:
2.如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,求证四边形ADOE是正方形.
D
·
O
A
B
C
E
证明:
∴四边形ADOE为矩形,
又 ∵AC=AB
∴ AE=AD
∴ 四边形ADOE为正方形.
教学程序
合作交流,归纳总结
① 本节课的过程、方法、内容是什么?
② 在圆中解决与弦有关问题时,经常做的辅助线是什么?
教学程序
1、必做题:教材87页练习1,2
2、选做题:古人常将玉璜(huáng)悬挂于胸前.你能利用所学的结论,帮助考古学家确定这个璜的
佩戴绳孔的位置吗?
(提示:绳孔在璜的中间
偏上位置.)
耐心填一填:
如图1,在圆O中,若MN⊥AB,MN为直径, 则_________, ____________, ___________.
·
M
O
A
B
N
C
2. 如图2,已知圆O的半径OA长为5,直径MN垂直于AB,AB长为8, 则OC的长为( )
A. 3 B. 6 C. 9 D. 10
3. 如图2:MN为圆O的直径,AB为弦,MN垂直于AB于 点C,则下列结论错误的是( )
A. ∠AOC=∠ BOC B.AC=BC C.MC=NC D.AN=BN
4、圆的半径为3,则弦长x的取值范围是__________.
5、若圆心到该圆的两条平行弦的距离分别是3和5,则此二条平行弦之间的距离是______________.
AC=BC
A
C
⌒
⌒
AN=BN
⌒
⌒
AM=BM
⌒
⌒
0<x≤6
2或8
·
M
N
O
A
B
图2
图1
C
同课章节目录
