新人教版数学七年级下 5.3.1平行线的性质
文档属性
| 名称 | 新人教版数学七年级下 5.3.1平行线的性质 |

|
|
| 格式 | rar | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-11 00:00:00 | ||
图片预览



文档简介
(共27张PPT)
数学组 宋莺歌
复习回顾
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定方法有哪些?
复习回顾
两直线平行
同位角相等
内错角相等
同旁内角互补
角的数量关系
直线的位置关系
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢
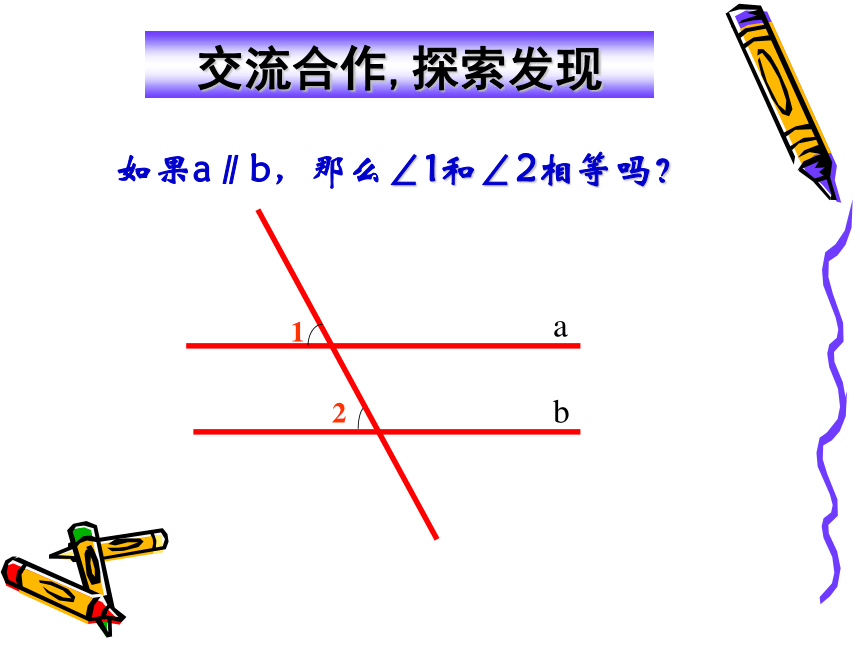
交流合作,探索发现
如果a∥b,那么∠1和∠2相等吗?
a
b
1
2
65°
65°
c
a
b
1
2
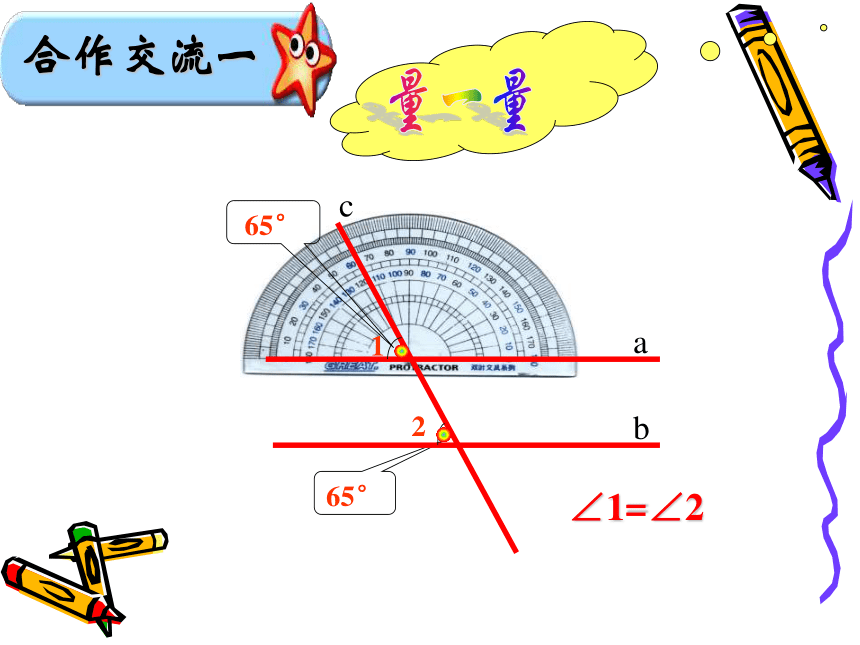
合作交流一
∠1=∠2
b
2
a
c
1
∠1=∠2
b
2
a
c
1
∠1=∠2
是不是任意一条直线去截平行线a、b
所得的同位角都相等呢?
b
1
2
a
c
两直线平行,同位角相等.
平行线的性质1
结论
两条平行线被第三条直线所截,
同位角相等.
性质发现
∴∠1=∠2
∵a∥b
简写为:
符号语言:
b
1
2
a
c
如图:已知a//b,那么 2与 3相等吗?
为什么
解∵a∥b(已知),
∴∠1=∠2(两直线平行,
同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
合作交流二
b
1
2
a
c
3
两直线平行,内错角相等.
平行线的性质2
结论
两条平行线被第三条直线所截,
内错角相等.
性质发现
∴∠2=∠3
∵a∥b
符号语言:
简写为:
b
1
2
a
c
3
解: ∵a//b (已知),
如图,已知a//b,那么 2与 4有什么关系呢?为什么
合作交流三
b
1
2
a
c
4
∴ 1= 2(两直线平行, 同位角相等).
∵ 1+ 4=180° (邻补角定义),
∴ 2+ 4=180° (等量代换).
解: ∵a//b (已知),
如图,已知a//b,那么 2与 4有什么关系呢?为什么
合作交流三
b
1
2
a
c
4
∴ 1= 2(两直线平行, 内错角相等)
∵ 1+ 4=180° (邻补角定义)
∴ 2+ 4=180° (等量代换)
两直线平行,同旁内角互补.
平行线的性质3
结论
两条平行线被第三条直线所截,
同旁内角互补.
性质发现
∴ 2+ 4=180°
∵a∥b
符号语言:
简写为:
b
1
2
a
c
4
两直线平行
同位角相等
内错角相等
同旁内角互补
两直线平行
同位角相等
内错角相等
同旁内角互补
判定
性质
如果没有两直线平行,同位角还相等吗?
师生互动,典例示范
例 如图,已知直线a∥b,
∠1 = 500,求∠2的度数.
a
b
c
1
2
∴∠ 2= 500
解:∵ a∥b(已知),
∴∠ 1= ∠ 2
(两直线平行,内错角相等).
又∵∠ 1 = 500 (已知),
变式1:已知条件不变,求∠3,∠4的度数?
3
4
变式2: 已知∠3 =∠4,∠1=50°,
求∠2的度数?
∴∠ 2= 50o
解:∵ ∠3 =∠4( )
∴a∥b
( )
又∵∠ 1 = 50o ( )
c
1
2
3
4
a
b
d
∴∠ 1= ∠ 2
( )
根据右边的图形,在括号内填上相应的理由:
①∵∠1=∠C( )
∴AB∥CD( )
②∵AB∥CD( )
∴ ∠3=∠C( )
③ ∵∠2+∠B=180°( )
∴EC∥BD( )
④ ∵∠1=∠B( )
∴EC∥BD( )
⑤ ∵EC∥BD( )
∴ ∠3=∠B( )
⑥ ∵AB∥CD( )
∴ ∠2+∠C= 180° ( )
E
A
C
D
B
1
2
3
4
同位角相等,两直线平行
内错角相等,两直线平行
已知
已知
已知
已知
已知
已知
两直线平行,内错角相等
同旁内角互补,两直线平行
两直线平行,同位角相等
两直线平行,同旁内角互补
注意:平行线的性质和判定的区别
如图,一辆汽车经过一条公路两次拐弯后,和原来的方向相同,也就是拐弯前后的两条路互相平行.第一次拐的角∠B等于1390,第二次拐的角∠C是多少度?为什么?
1390
B
C
A
D
?
解:
∵AB∥CD (已知),
∴∠B=∠C
(两直线平行,
内错角相等).
又∵∠B=139° (已知),
∴∠C=∠B=139°
(等量代换).
学以致用
量得∠A=115°, ∠D=100°
两直线平行
同位角相等
内错角相等
同旁内角互补
直线的位置关系
角的数量关系
判定
性质
平行线的性质和平行线的判定方法的 区 别 与 联 系
小结
课本23页:
作业: 4, 5
选做:7
数学组 宋莺歌
复习回顾
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定方法有哪些?
复习回顾
两直线平行
同位角相等
内错角相等
同旁内角互补
角的数量关系
直线的位置关系
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢
交流合作,探索发现
如果a∥b,那么∠1和∠2相等吗?
a
b
1
2
65°
65°
c
a
b
1
2
合作交流一
∠1=∠2
b
2
a
c
1
∠1=∠2
b
2
a
c
1
∠1=∠2
是不是任意一条直线去截平行线a、b
所得的同位角都相等呢?
b
1
2
a
c
两直线平行,同位角相等.
平行线的性质1
结论
两条平行线被第三条直线所截,
同位角相等.
性质发现
∴∠1=∠2
∵a∥b
简写为:
符号语言:
b
1
2
a
c
如图:已知a//b,那么 2与 3相等吗?
为什么
解∵a∥b(已知),
∴∠1=∠2(两直线平行,
同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
合作交流二
b
1
2
a
c
3
两直线平行,内错角相等.
平行线的性质2
结论
两条平行线被第三条直线所截,
内错角相等.
性质发现
∴∠2=∠3
∵a∥b
符号语言:
简写为:
b
1
2
a
c
3
解: ∵a//b (已知),
如图,已知a//b,那么 2与 4有什么关系呢?为什么
合作交流三
b
1
2
a
c
4
∴ 1= 2(两直线平行, 同位角相等).
∵ 1+ 4=180° (邻补角定义),
∴ 2+ 4=180° (等量代换).
解: ∵a//b (已知),
如图,已知a//b,那么 2与 4有什么关系呢?为什么
合作交流三
b
1
2
a
c
4
∴ 1= 2(两直线平行, 内错角相等)
∵ 1+ 4=180° (邻补角定义)
∴ 2+ 4=180° (等量代换)
两直线平行,同旁内角互补.
平行线的性质3
结论
两条平行线被第三条直线所截,
同旁内角互补.
性质发现
∴ 2+ 4=180°
∵a∥b
符号语言:
简写为:
b
1
2
a
c
4
两直线平行
同位角相等
内错角相等
同旁内角互补
两直线平行
同位角相等
内错角相等
同旁内角互补
判定
性质
如果没有两直线平行,同位角还相等吗?
师生互动,典例示范
例 如图,已知直线a∥b,
∠1 = 500,求∠2的度数.
a
b
c
1
2
∴∠ 2= 500
解:∵ a∥b(已知),
∴∠ 1= ∠ 2
(两直线平行,内错角相等).
又∵∠ 1 = 500 (已知),
变式1:已知条件不变,求∠3,∠4的度数?
3
4
变式2: 已知∠3 =∠4,∠1=50°,
求∠2的度数?
∴∠ 2= 50o
解:∵ ∠3 =∠4( )
∴a∥b
( )
又∵∠ 1 = 50o ( )
c
1
2
3
4
a
b
d
∴∠ 1= ∠ 2
( )
根据右边的图形,在括号内填上相应的理由:
①∵∠1=∠C( )
∴AB∥CD( )
②∵AB∥CD( )
∴ ∠3=∠C( )
③ ∵∠2+∠B=180°( )
∴EC∥BD( )
④ ∵∠1=∠B( )
∴EC∥BD( )
⑤ ∵EC∥BD( )
∴ ∠3=∠B( )
⑥ ∵AB∥CD( )
∴ ∠2+∠C= 180° ( )
E
A
C
D
B
1
2
3
4
同位角相等,两直线平行
内错角相等,两直线平行
已知
已知
已知
已知
已知
已知
两直线平行,内错角相等
同旁内角互补,两直线平行
两直线平行,同位角相等
两直线平行,同旁内角互补
注意:平行线的性质和判定的区别
如图,一辆汽车经过一条公路两次拐弯后,和原来的方向相同,也就是拐弯前后的两条路互相平行.第一次拐的角∠B等于1390,第二次拐的角∠C是多少度?为什么?
1390
B
C
A
D
?
解:
∵AB∥CD (已知),
∴∠B=∠C
(两直线平行,
内错角相等).
又∵∠B=139° (已知),
∴∠C=∠B=139°
(等量代换).
学以致用
量得∠A=115°, ∠D=100°
两直线平行
同位角相等
内错角相等
同旁内角互补
直线的位置关系
角的数量关系
判定
性质
平行线的性质和平行线的判定方法的 区 别 与 联 系
小结
课本23页:
作业: 4, 5
选做:7
