圆周角 2
图片预览


文档简介
(共22张PPT)
24.1.4圆周角(2)
特征:
① 角的顶点在圆上.
② 角的两边都与圆相交.
1、圆周角定义: 顶点在圆上,
并且两边都和圆相交的角叫圆周角.
一、旧知回放:
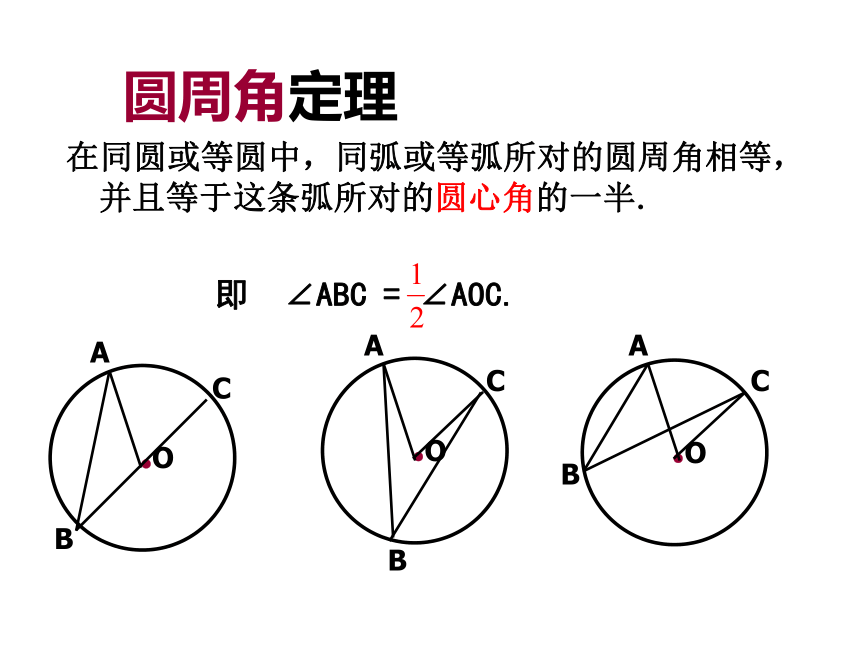
圆周角定理
在同圆或等圆中,同弧或等弧所对的圆周角相等,并且等于这条弧所对的圆心角的一半.
●O
A
B
C
●O
A
B
C
●O
A
B
C
即 ∠ABC = ∠AOC.
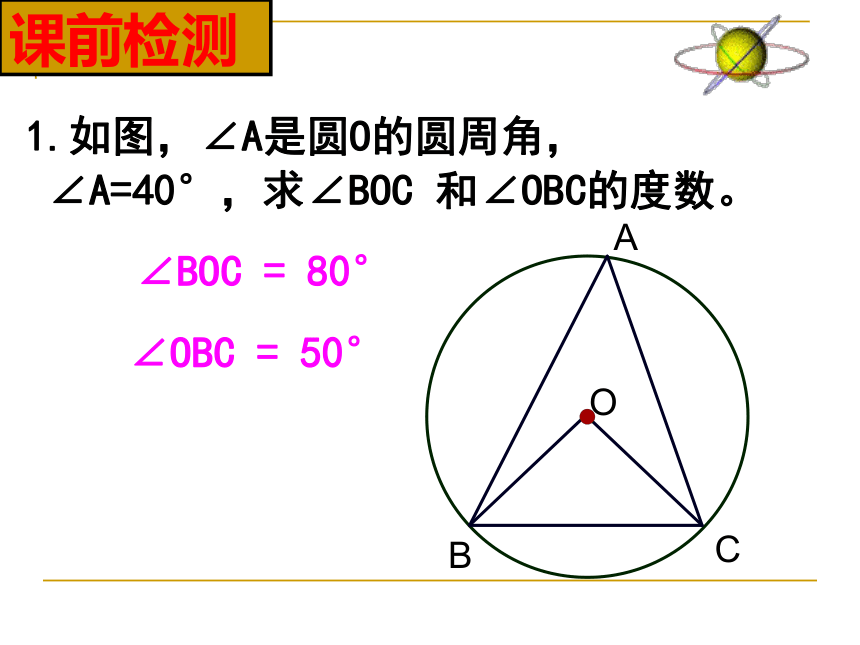
1.如图,∠A是圆O的圆周角,
∠A=40°,求∠BOC 和∠OBC的度数。
课前检测
∠BOC = 80°
∠OBC = 50°
练一练
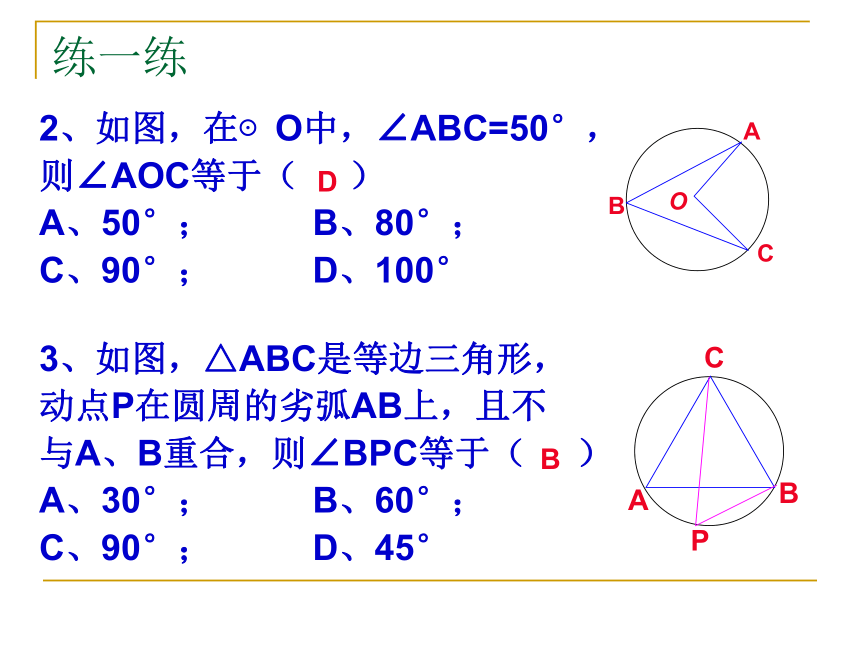
2、如图,在⊙O中,∠ABC=50°,
则∠AOC等于( )
A、50°; B、80°;
C、90°; D、100°
A
C
B
O
D
3、如图,△ABC是等边三角形,
动点P在圆周的劣弧AB上,且不
与A、B重合,则∠BPC等于( )
A、30°; B、60°;
C、90°; D、45°
C
A
B
P
B
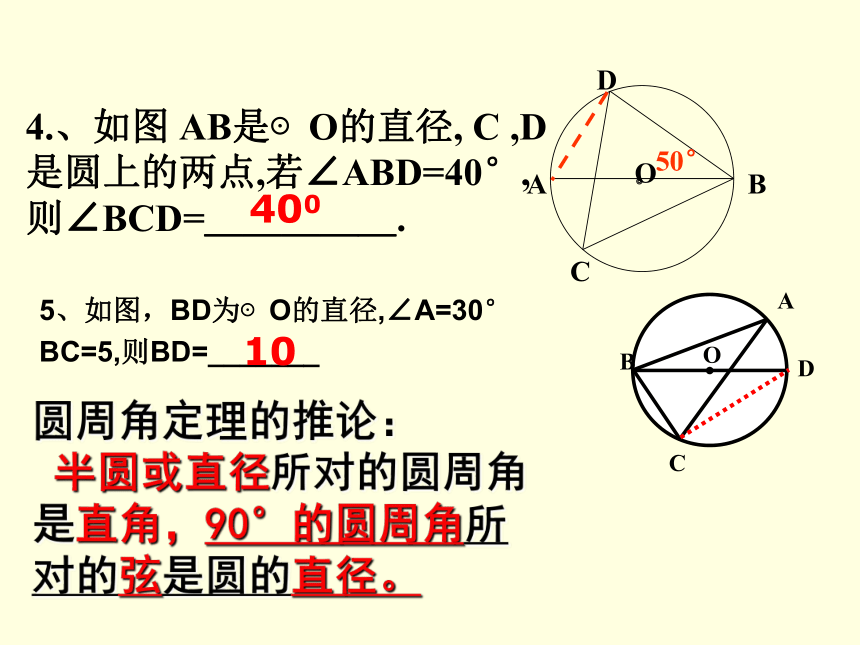
4.、如图 AB是⊙O的直径, C ,D是圆上的两点,若∠ABD=40°,则∠BCD=_____.
A
B
O
C
D
50°
5、如图,BD为⊙O的直径,∠A=30°
BC=5,则BD=_______
B
C
D
A
O
400
10
半圆或直径所对的圆周角是直角,90°的圆周角所对的弦是圆的直径。
圆周角定理的推论:
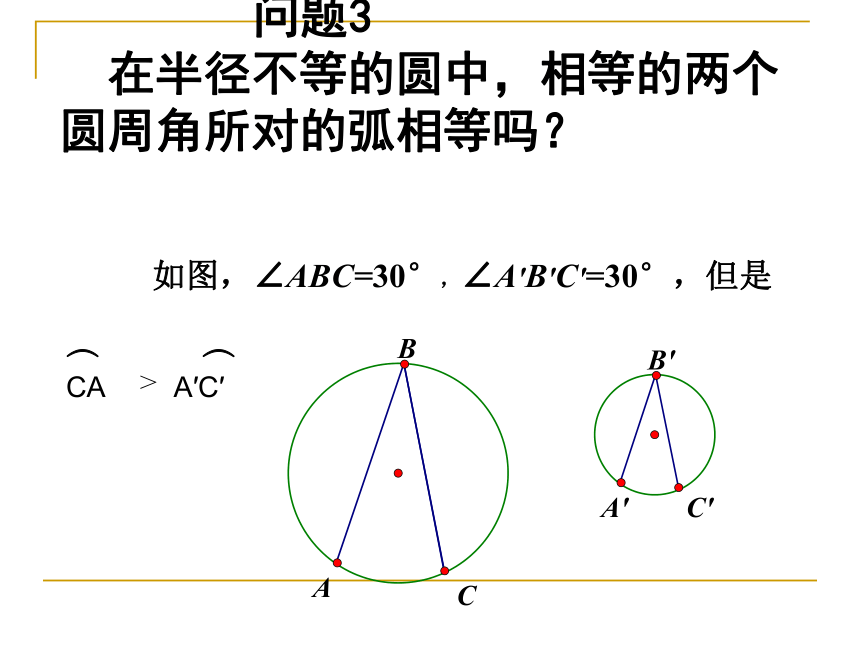
问题3
在半径不等的圆中,相等的两个圆周角所对的弧相等吗?
C
A'
B
B'
A
C'
如图,∠ABC=30°,∠A′B′C′=30°,但是
︵
︵
CA
A′C′
>
在同圆或等圆中,如果两个圆周角相等,
它们所对的弧一定相等吗?为什么?
A′
B
B′
A
C
C′
O
因为在同圆或等圆中,如果两个圆周角相等,
它们的圆心角也相等,则它们所对的弧一定相等。
结论
在同圆或等圆中,如果两个圆周角相等,那么它们所对的弧一定相等。
课堂检测
1.已知,四边形ABCD的顶点在⊙O上, ∠BCD=120°,则∠BAD 。
A
B
C
D
O
60°
圆内接多边形与多边形的外接圆:
如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形;
例如:如图,四边形ABCD是⊙O的 ;
⊙O是四边形ABCD的 .
探究:圆内接四边形的对角有什么关系?
内接多边形
外接圆
这个圆叫做这个多边形的外接圆.
证明:已知:如图,四边形ABCD的四个顶点在⊙O上,求证:∠A+∠C=1800
A
B
C
D
O
圆内接四边形的一个性质:
圆内接四边形的对角互补.
O
C
B
A
D
练习:如图, B是AC上的一点,∠AOC=105°,求∠ABC和∠ADC的度数 。
⌒
例 如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长.
又在Rt△ABD中,AD2+BD2=AB2,
解:∵AB是直径,
∴ ∠ACB= ∠ADB=90°.
在Rt△ABC中,
∵CD平分∠ACB,
∴AD=BD.
例题
3.求证:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.(提示:作出以这条边为直径的圆.)
·
A
B
C
O
求证: △ABC 为直角三角形.
证明:
CO= AB,
以AB为直径作⊙O,
∵AO=BO,
∴AO=BO=CO.
∴点C在⊙O上.
又∵AB为直径,
∴∠ACB= ×180°= 90°.
已知:△ABC 中,CO为AB边上的中线,
且CO= AB
∴ △ABC 为直角三角形.
课本 练 习
小结:
1、圆周角定理:同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
2、圆周角定理的推论:直径所对的圆周角是直角,900的圆周角所对的弦是直径.
3、应用:求角的度数,证明角、线段、弧的相等关系.
(在圆中,常作直径,构造直角三角形)
1、100 的弧所对的圆心角等于_______,所对的圆周角等于_______。
2、一弦分圆周角成两部分,其中一部分是另一部分的4倍,则这弦所对的圆周角度数为________________。
3、如图,在⊙O中,∠BAC=32 ,则∠BOC=________。
4、如图,⊙O中,∠ACB = 130 ,则∠AOB=______。
5、下列命题中是真命题的是( )
(A)顶点在圆周上的角叫做圆周角。
(B)60 的圆周角所对的弧的度数是30
(C)一弧所对的圆周角等于它所对的圆心角。
(D)120 的弧所对的圆周角是60
A
O
C
B
B
A
O
C
100
50
36 或144
64
100
D
练习
C
D
A
B
E
补充例题:
平分已知弧AB
已知:弧AB
作法:
⒈ 连结AB.
⒉作AB的垂直平分线 CD,交弧AB于点E.
∴点E就是所求弧AB的中点。
求作:弧AB的中点
因此,在点B射门为好。
如图,在足球比赛中,甲、乙两名队
员互相配合向对方球门MN进攻,当
甲带球冲到A点时,乙已跟随冲到B点,此时自己直接射门好,还是迅速将球回传给乙,让乙射门好?
(在射门时球员相对与球门的张角越大射门的成功率就越大。)
解:
过M、N、B作圆,则点A在圆外
因为∠A<∠MCN
而∠MCN= ∠O= ∠B
∴∠A<∠B
连接M、C
24.1.4圆周角(2)
特征:
① 角的顶点在圆上.
② 角的两边都与圆相交.
1、圆周角定义: 顶点在圆上,
并且两边都和圆相交的角叫圆周角.
一、旧知回放:
圆周角定理
在同圆或等圆中,同弧或等弧所对的圆周角相等,并且等于这条弧所对的圆心角的一半.
●O
A
B
C
●O
A
B
C
●O
A
B
C
即 ∠ABC = ∠AOC.
1.如图,∠A是圆O的圆周角,
∠A=40°,求∠BOC 和∠OBC的度数。
课前检测
∠BOC = 80°
∠OBC = 50°
练一练
2、如图,在⊙O中,∠ABC=50°,
则∠AOC等于( )
A、50°; B、80°;
C、90°; D、100°
A
C
B
O
D
3、如图,△ABC是等边三角形,
动点P在圆周的劣弧AB上,且不
与A、B重合,则∠BPC等于( )
A、30°; B、60°;
C、90°; D、45°
C
A
B
P
B
4.、如图 AB是⊙O的直径, C ,D是圆上的两点,若∠ABD=40°,则∠BCD=_____.
A
B
O
C
D
50°
5、如图,BD为⊙O的直径,∠A=30°
BC=5,则BD=_______
B
C
D
A
O
400
10
半圆或直径所对的圆周角是直角,90°的圆周角所对的弦是圆的直径。
圆周角定理的推论:
问题3
在半径不等的圆中,相等的两个圆周角所对的弧相等吗?
C
A'
B
B'
A
C'
如图,∠ABC=30°,∠A′B′C′=30°,但是
︵
︵
CA
A′C′
>
在同圆或等圆中,如果两个圆周角相等,
它们所对的弧一定相等吗?为什么?
A′
B
B′
A
C
C′
O
因为在同圆或等圆中,如果两个圆周角相等,
它们的圆心角也相等,则它们所对的弧一定相等。
结论
在同圆或等圆中,如果两个圆周角相等,那么它们所对的弧一定相等。
课堂检测
1.已知,四边形ABCD的顶点在⊙O上, ∠BCD=120°,则∠BAD 。
A
B
C
D
O
60°
圆内接多边形与多边形的外接圆:
如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形;
例如:如图,四边形ABCD是⊙O的 ;
⊙O是四边形ABCD的 .
探究:圆内接四边形的对角有什么关系?
内接多边形
外接圆
这个圆叫做这个多边形的外接圆.
证明:已知:如图,四边形ABCD的四个顶点在⊙O上,求证:∠A+∠C=1800
A
B
C
D
O
圆内接四边形的一个性质:
圆内接四边形的对角互补.
O
C
B
A
D
练习:如图, B是AC上的一点,∠AOC=105°,求∠ABC和∠ADC的度数 。
⌒
例 如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长.
又在Rt△ABD中,AD2+BD2=AB2,
解:∵AB是直径,
∴ ∠ACB= ∠ADB=90°.
在Rt△ABC中,
∵CD平分∠ACB,
∴AD=BD.
例题
3.求证:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.(提示:作出以这条边为直径的圆.)
·
A
B
C
O
求证: △ABC 为直角三角形.
证明:
CO= AB,
以AB为直径作⊙O,
∵AO=BO,
∴AO=BO=CO.
∴点C在⊙O上.
又∵AB为直径,
∴∠ACB= ×180°= 90°.
已知:△ABC 中,CO为AB边上的中线,
且CO= AB
∴ △ABC 为直角三角形.
课本 练 习
小结:
1、圆周角定理:同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
2、圆周角定理的推论:直径所对的圆周角是直角,900的圆周角所对的弦是直径.
3、应用:求角的度数,证明角、线段、弧的相等关系.
(在圆中,常作直径,构造直角三角形)
1、100 的弧所对的圆心角等于_______,所对的圆周角等于_______。
2、一弦分圆周角成两部分,其中一部分是另一部分的4倍,则这弦所对的圆周角度数为________________。
3、如图,在⊙O中,∠BAC=32 ,则∠BOC=________。
4、如图,⊙O中,∠ACB = 130 ,则∠AOB=______。
5、下列命题中是真命题的是( )
(A)顶点在圆周上的角叫做圆周角。
(B)60 的圆周角所对的弧的度数是30
(C)一弧所对的圆周角等于它所对的圆心角。
(D)120 的弧所对的圆周角是60
A
O
C
B
B
A
O
C
100
50
36 或144
64
100
D
练习
C
D
A
B
E
补充例题:
平分已知弧AB
已知:弧AB
作法:
⒈ 连结AB.
⒉作AB的垂直平分线 CD,交弧AB于点E.
∴点E就是所求弧AB的中点。
求作:弧AB的中点
因此,在点B射门为好。
如图,在足球比赛中,甲、乙两名队
员互相配合向对方球门MN进攻,当
甲带球冲到A点时,乙已跟随冲到B点,此时自己直接射门好,还是迅速将球回传给乙,让乙射门好?
(在射门时球员相对与球门的张角越大射门的成功率就越大。)
解:
过M、N、B作圆,则点A在圆外
因为∠A<∠MCN
而∠MCN= ∠O= ∠B
∴∠A<∠B
连接M、C
同课章节目录
