24.1.1 圆
图片预览






文档简介
(共18张PPT)
24.1.1 圆
古希腊数学家毕达哥拉斯认为:
一切立体图形中最美的是球;
一切平面图形中最美的是圆。
一、 创设情境 引入新课
圆是一种基本的几何图形,圆形物体在生活中随处可见,例如:
活动1
观察下列画圆的过程,你能由此说出圆的形成过程吗?
.
O
A
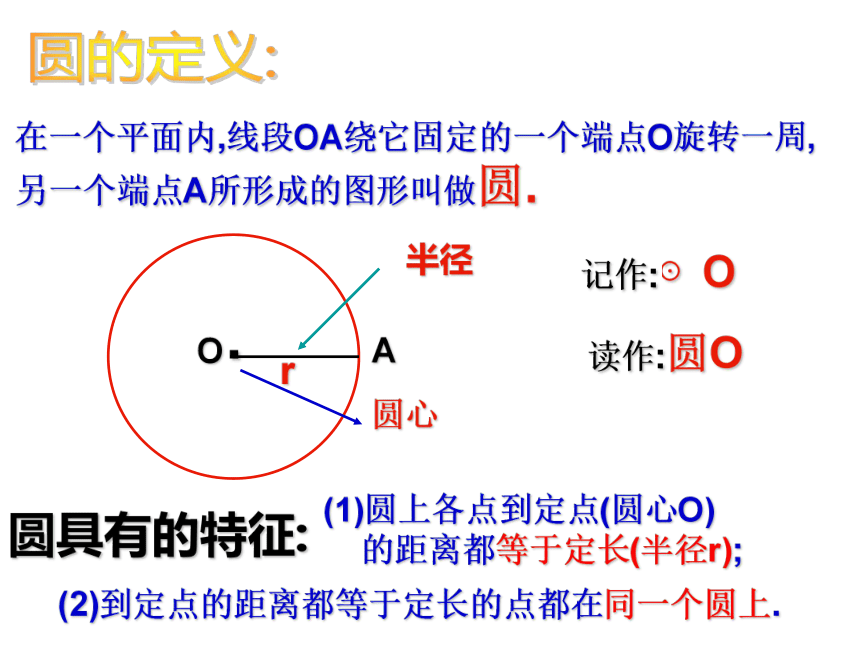
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.
圆心
半径
r
记作:⊙O
读作:圆O
(1)圆上各点到定点(圆心O)
的距离都等于定长(半径r);
(2)到定点的距离都等于定长的点都在同一个圆上.
圆具有的特征:
●
要确定一个圆,必须确定圆的____和____
圆心
半径
圆心确定圆的位置,半径确定圆的大小.
O
根据圆的定义,“圆”指的是“ 圆周 ”,是曲线,而不是“圆面”。
到定点O的距离等于定长r的点组成的图形叫做圆。
车轮为什么做成圆形
应 用 新 知
把车轮做成圆形,车轮上各点到车轮中心(圆心)
的距离都等于车轮的半径,
当车轮在平面上滚动时,
车轮中心与平面的距离
保持不变。因此,
当车辆在平坦的路上行使时,
坐车的人会感觉到非常平稳,
这也是车轮都做成圆形的
数学道理。
思考:你能说出为什么车轮不弄成正方形?
.
O
A
B
C
弦
连接圆上任意两点的线段,
直径
经过圆心的弦。
弦
直径
注意:
凡直径都是弦,是圆中最长的弦
但弦不一定是直径.
圆中有关概念:
图中线段AB、AC。
图中线段AB。
即时考你:
.
O
A
D
Q
C
B
P
H
G
F
E
如图(1)直径是_______;
(2)弦是_____________;
(3) PQ是直径吗 ______;
(4)线段EF、GH
是弦吗?_______.
K
AB
CD、DK、AB
不是
不是
●
O
B
C
A
1.如图,半径有:______________
OA、OB、OC
若∠AOB=60°,
则△AOB是_____三角形.
2.如图,弦有:______________
AB、BC、
AC
等边
直径是圆中最长的弦。
圆弧:连接圆上任意两点间的部分叫做圆弧,简称弧.
以A、C为端点的弧记作 AC ,
读作:“圆弧AC”或“弧AC”。
大于半圆的弧(用三个点表示,如: 或 ),
叫做优弧;
小于半圆的弧叫做劣弧. 如:
圆的任意一条直径的两个端点把圆分成两条弧,
每一条弧叫做半圆.
圆中有关概念:
●
O
B
C
A
1.如图,弧有:______________
⌒
AB
⌒
BC
⌒
ABC
⌒
ACB
⌒
BCA
它们一样么?
⌒
AB
⌒
BC
2 .劣弧有:
优弧有:
⌒
ACB
⌒
BAC
你知道优弧与劣弧的区别么?
能够互相重合的弧是等弧。
能够重合的两个圆叫做等圆。
练一练
一、判断题:
1、直径是弦。( )
2、弦是直径。( )
3、半圆是弧,但弧不一定是半圆。( )
4、半径相等的两个半圆是等弧。( )
5、长度相等的弧是等弧。( )
二、选择
1、以点O为圆心作圆可以作( )
A、1个; B、2个; C、3个; D、无数个。
2、如图,点A、O、D以及B、O、C分别在一条
直线上,则圆中的弦的条数为( )
A、2; B、3; C、4; D、5
C
A
E
B
D
O
×
×
D
√
√
√
A
基础训练
1.过圆上一点可以作圆的最长弦有( )条.
A. 1 B. 2 C. 3 D.无数条
2.圆内一点和⊙O上的最近点距离为4cm,最远距离为10cm,
则这个圆的半径是______cm.
3.图中有____条直径,____条非直径的弦,圆中以A为一个
端点的优弧有____条,劣弧有____条.
4.如图, ⊙O中,点A、O、D以及点B、O、C分别在一直线
上,图中弦的条数为_____。
5.CD为⊙O的直径,∠EOD=72°,AE交⊙O于B,
且AB=OC,则∠A=_______.
D
7
1
2
2
4
2
第5题
24°
6、圆的半径为1cm,它的周长是 ;
面积是 。
7、下列说法中,下确是有( )
(1)直径是圆中最长的弦;(2)弧AB的长度大于弦AB的长度;(3)直径的中心是圆心;(4)不在圆上的点到圆心的距离不等于半径。
A4个 B3个 C2个 D1个
8、根据下列条件画圆:
(1)以O 为圆心,画两个圆;
(2)以O 为圆心,半径为1.5cm;
(3)已知AB=4cm,画一个圆,使AB是它的直径。
9、在A地往南40m的B处有一幢民宅,东30m的C处有一变电设施,在 BC的中点D处有一古建筑,因施工需要必须在A处进行一次爆破,为使民宅、变 电设施、古建筑都不遭到破坏,则爆破影响面的半径r应控制的范围为____________。
算出距离 AB=40 AC=30 设AC中点为E,DE=1/2AB=20 又DE垂直AE AE=15 所以AD=25 三个边最小的为AD 所以小于25即可.
24.1.1 圆
古希腊数学家毕达哥拉斯认为:
一切立体图形中最美的是球;
一切平面图形中最美的是圆。
一、 创设情境 引入新课
圆是一种基本的几何图形,圆形物体在生活中随处可见,例如:
活动1
观察下列画圆的过程,你能由此说出圆的形成过程吗?
.
O
A
在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.
圆心
半径
r
记作:⊙O
读作:圆O
(1)圆上各点到定点(圆心O)
的距离都等于定长(半径r);
(2)到定点的距离都等于定长的点都在同一个圆上.
圆具有的特征:
●
要确定一个圆,必须确定圆的____和____
圆心
半径
圆心确定圆的位置,半径确定圆的大小.
O
根据圆的定义,“圆”指的是“ 圆周 ”,是曲线,而不是“圆面”。
到定点O的距离等于定长r的点组成的图形叫做圆。
车轮为什么做成圆形
应 用 新 知
把车轮做成圆形,车轮上各点到车轮中心(圆心)
的距离都等于车轮的半径,
当车轮在平面上滚动时,
车轮中心与平面的距离
保持不变。因此,
当车辆在平坦的路上行使时,
坐车的人会感觉到非常平稳,
这也是车轮都做成圆形的
数学道理。
思考:你能说出为什么车轮不弄成正方形?
.
O
A
B
C
弦
连接圆上任意两点的线段,
直径
经过圆心的弦。
弦
直径
注意:
凡直径都是弦,是圆中最长的弦
但弦不一定是直径.
圆中有关概念:
图中线段AB、AC。
图中线段AB。
即时考你:
.
O
A
D
Q
C
B
P
H
G
F
E
如图(1)直径是_______;
(2)弦是_____________;
(3) PQ是直径吗 ______;
(4)线段EF、GH
是弦吗?_______.
K
AB
CD、DK、AB
不是
不是
●
O
B
C
A
1.如图,半径有:______________
OA、OB、OC
若∠AOB=60°,
则△AOB是_____三角形.
2.如图,弦有:______________
AB、BC、
AC
等边
直径是圆中最长的弦。
圆弧:连接圆上任意两点间的部分叫做圆弧,简称弧.
以A、C为端点的弧记作 AC ,
读作:“圆弧AC”或“弧AC”。
大于半圆的弧(用三个点表示,如: 或 ),
叫做优弧;
小于半圆的弧叫做劣弧. 如:
圆的任意一条直径的两个端点把圆分成两条弧,
每一条弧叫做半圆.
圆中有关概念:
●
O
B
C
A
1.如图,弧有:______________
⌒
AB
⌒
BC
⌒
ABC
⌒
ACB
⌒
BCA
它们一样么?
⌒
AB
⌒
BC
2 .劣弧有:
优弧有:
⌒
ACB
⌒
BAC
你知道优弧与劣弧的区别么?
能够互相重合的弧是等弧。
能够重合的两个圆叫做等圆。
练一练
一、判断题:
1、直径是弦。( )
2、弦是直径。( )
3、半圆是弧,但弧不一定是半圆。( )
4、半径相等的两个半圆是等弧。( )
5、长度相等的弧是等弧。( )
二、选择
1、以点O为圆心作圆可以作( )
A、1个; B、2个; C、3个; D、无数个。
2、如图,点A、O、D以及B、O、C分别在一条
直线上,则圆中的弦的条数为( )
A、2; B、3; C、4; D、5
C
A
E
B
D
O
×
×
D
√
√
√
A
基础训练
1.过圆上一点可以作圆的最长弦有( )条.
A. 1 B. 2 C. 3 D.无数条
2.圆内一点和⊙O上的最近点距离为4cm,最远距离为10cm,
则这个圆的半径是______cm.
3.图中有____条直径,____条非直径的弦,圆中以A为一个
端点的优弧有____条,劣弧有____条.
4.如图, ⊙O中,点A、O、D以及点B、O、C分别在一直线
上,图中弦的条数为_____。
5.CD为⊙O的直径,∠EOD=72°,AE交⊙O于B,
且AB=OC,则∠A=_______.
D
7
1
2
2
4
2
第5题
24°
6、圆的半径为1cm,它的周长是 ;
面积是 。
7、下列说法中,下确是有( )
(1)直径是圆中最长的弦;(2)弧AB的长度大于弦AB的长度;(3)直径的中心是圆心;(4)不在圆上的点到圆心的距离不等于半径。
A4个 B3个 C2个 D1个
8、根据下列条件画圆:
(1)以O 为圆心,画两个圆;
(2)以O 为圆心,半径为1.5cm;
(3)已知AB=4cm,画一个圆,使AB是它的直径。
9、在A地往南40m的B处有一幢民宅,东30m的C处有一变电设施,在 BC的中点D处有一古建筑,因施工需要必须在A处进行一次爆破,为使民宅、变 电设施、古建筑都不遭到破坏,则爆破影响面的半径r应控制的范围为____________。
算出距离 AB=40 AC=30 设AC中点为E,DE=1/2AB=20 又DE垂直AE AE=15 所以AD=25 三个边最小的为AD 所以小于25即可.
同课章节目录
