高中数学人教A版必修2课件-2.1.1平面(23张PPT)
文档属性
| 名称 | 高中数学人教A版必修2课件-2.1.1平面(23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-12 22:12:46 | ||
图片预览





文档简介
立体几何中的平面的特点:
2.四周无限延展
(没有边界)
3.不计大小
(无所谓面积)
4.不计厚薄
(没有体积)
1.平的
(不是凹凸不平)
1.平面
(2)直线可以看成是点的集合,所以平面可视为直线的集合,也可视为点的集合.
(3)和点、直线一样,平面也是从现实世界中抽象出来的几何概念,它没有厚薄,是无限延展的.
(1)平面可以看成是一条直线沿着某一方向平移等到的.
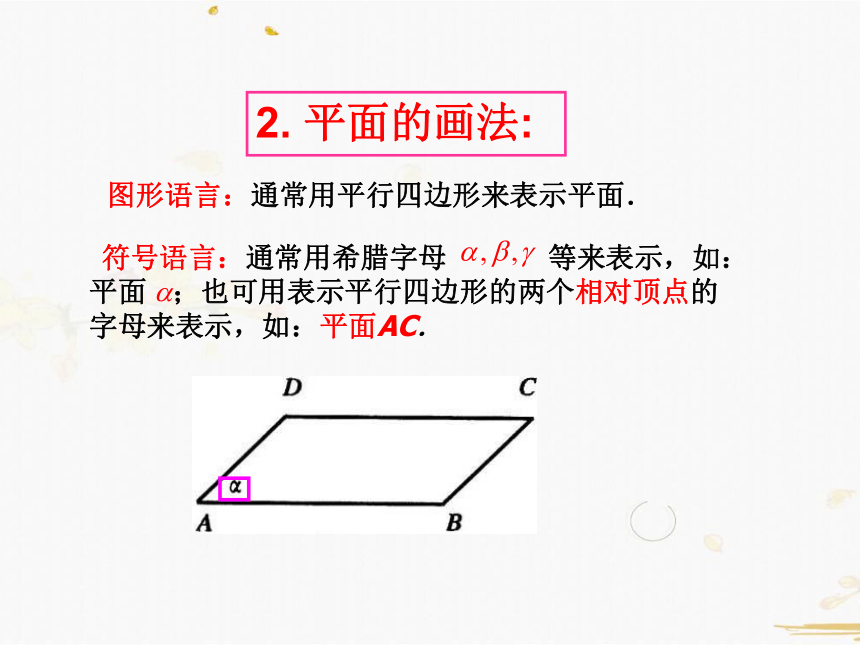
2. 平面的画法:
图形语言:通常用平行四边形来表示平面.
符号语言:通常用希腊字母 等来表示,如:平面 ;也可用表示平行四边形的两个相对顶点的字母来表示,如:平面AC.
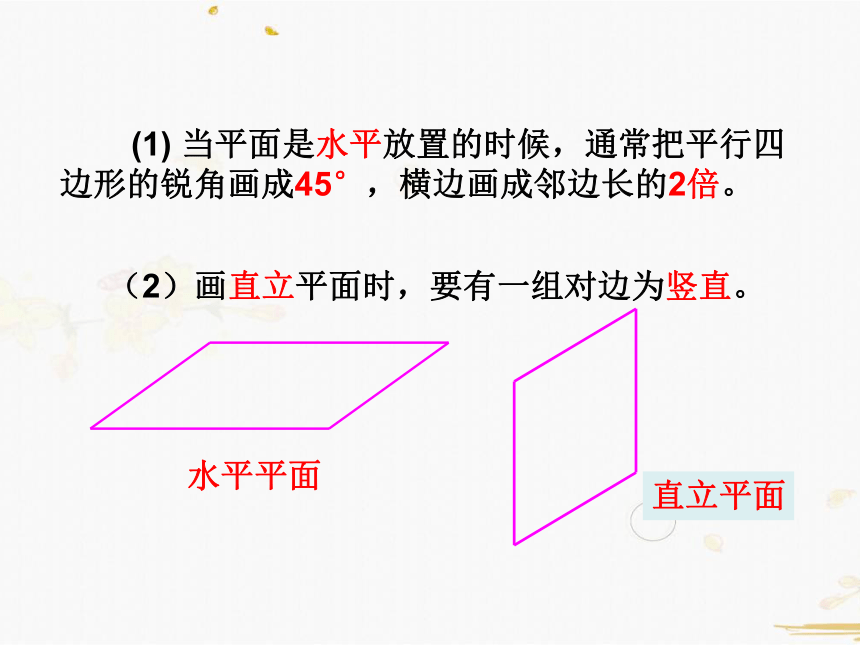
直立平面
水平平面
(1) 当平面是水平放置的时候,通常把平行四边形的锐角画成45°,横边画成邻边长的2倍。
(2)画直立平面时,要有一组对边为竖直。
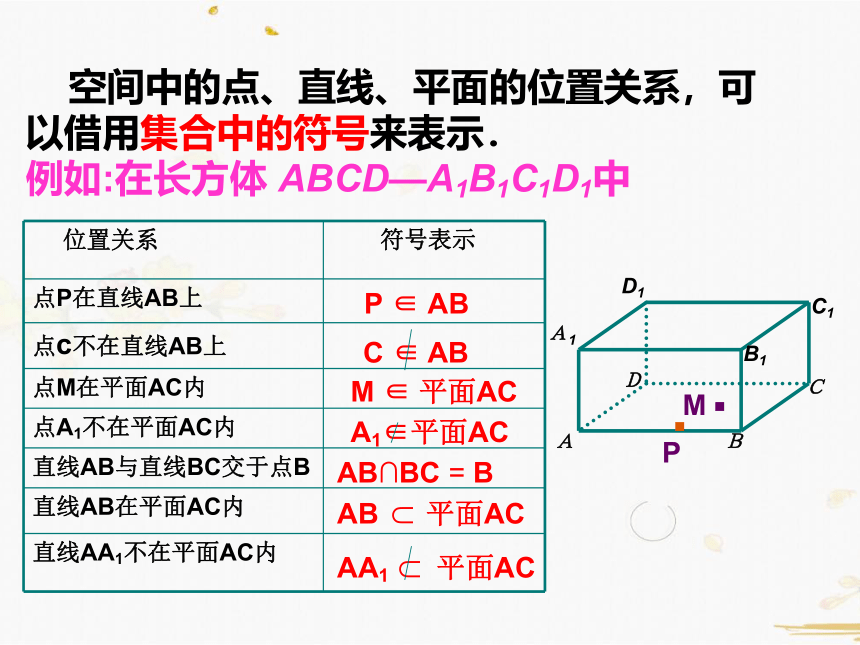
空间中的点、直线、平面的位置关系,可
以借用集合中的符号来表示.
例如:在长方体 ABCD—A1B1C1D1中
A
B
C
D
A1
B1
C1
D1
·
P
·
M
位置关系
符号表示
点P在直线AB上
点c不在直线AB上
点M在平面AC内
点A1不在平面AC内
直线AB与直线BC交于点B
直线AB在平面AC内
直线AA1不在平面AC内
P ∈ AB
C ∈ AB
M ∈ 平面AC
A1∈平面AC
AB∩BC = B
∩
AB 平面AC
∩
AA1 平面AC
例1.正方体的各顶点如图所示,正方体的三个面所在平面 ,分别记作 ,试用适当的符号填空.
∈
∈
∈
∈
∈
∈
∩
∩
∩
∩
∩
如果直线 l 与平面α有一个公共点P,直线 l 是否在平面α内?
平面公理
实际生活中,我们有这样的经验:把一根直尺边缘上的任意两点放到桌面上,可以看到,直尺的整个边缘就落在了桌面上.
如果直线 l 与平面α有两个公共点,直线 l 是否在平面α内?
平面公理
公理1 如果一条直线上的两点在一个平面内,那么这条直线在此平面内.
A
B
l
作用:
判定直线是否在平面内.
在生产、生活中,人们经过长期观察与实践,总结出关于平面的一些基本性质,我们把它作为公理.这些公理是进一步推理的基础.
平面公理
生活中经常看到用三角架支撑照相机.
平面公理
公理2 过不在一条直线上的三点,有且只有一个平面.
A
C
B
存在性
唯一性
作用:
确定平面的主要依据.
不在一条直线上的三个点A、B、C所确定的平面,可以记成“平面ABC”.
平面公理
推论2 经过两条相交直线,有且只有一个平面
推论3 经过两条平行直线,有且只有一个平面
推论1? 经过一条直线和这条直线外的一点,有
且只有一个平面
重要推论
把三角板的一个角立在课桌面上,三角板所在平面与桌面所在平面是否只相交于一点B?为什么?
B
平面公理
B
把三角板的一个角立在课桌面上,三角板所在平面与桌面所在平面是否只相交于一点B?为什么?
平面公理
观察长方体,你能发现长方体的两个相交平面有没有公共直线吗?
这条公共直线B’C’叫做这两个平面A’B’C’D’和平面BB’C’C的交线.
另一方面,相邻两个平面有一个公共点,如平面A’B’C’D’和平面BB’C’C有一个公共点B’,经过点B有且只有一条过该点的公共直线B’C’.
平面公理
公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
作用:
①判断两个平面相交的依据.
②判断点在直线上.
l
P
平面公理
例1 如图,用符号表示下列图形中点、直线、平面之间的位置关系.
a
l
A
B
a
l
P
b
(1)
(2)
解:在(1)中,
在(2)中,
典型例题
请叙述三条公理和三条推论
如果一条直线上的两点在一个平面内,那么这条直线在此平面内
过不在一条直线上的三点,有且只有一个平面
经过一条直线和这条直线外的一点有且只有一个平面
经过两条相交直线,有且只有一个平面
经过两条平行直线,有且只有一个平面
如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线
课堂练习:
P43页 1—4题
探究思考:
平面内一条直线把平面分成______部分
平面内两条直线可以把平面分成_________部分
平面内三条直线可以把平面分成_________部分
2
3或4
4或6或7
若三个平面两两相交有三条交线,若其中两条相交于一点,证明第三条交线也过这一点。
拓展练习
2.四周无限延展
(没有边界)
3.不计大小
(无所谓面积)
4.不计厚薄
(没有体积)
1.平的
(不是凹凸不平)
1.平面
(2)直线可以看成是点的集合,所以平面可视为直线的集合,也可视为点的集合.
(3)和点、直线一样,平面也是从现实世界中抽象出来的几何概念,它没有厚薄,是无限延展的.
(1)平面可以看成是一条直线沿着某一方向平移等到的.
2. 平面的画法:
图形语言:通常用平行四边形来表示平面.
符号语言:通常用希腊字母 等来表示,如:平面 ;也可用表示平行四边形的两个相对顶点的字母来表示,如:平面AC.
直立平面
水平平面
(1) 当平面是水平放置的时候,通常把平行四边形的锐角画成45°,横边画成邻边长的2倍。
(2)画直立平面时,要有一组对边为竖直。
空间中的点、直线、平面的位置关系,可
以借用集合中的符号来表示.
例如:在长方体 ABCD—A1B1C1D1中
A
B
C
D
A1
B1
C1
D1
·
P
·
M
位置关系
符号表示
点P在直线AB上
点c不在直线AB上
点M在平面AC内
点A1不在平面AC内
直线AB与直线BC交于点B
直线AB在平面AC内
直线AA1不在平面AC内
P ∈ AB
C ∈ AB
M ∈ 平面AC
A1∈平面AC
AB∩BC = B
∩
AB 平面AC
∩
AA1 平面AC
例1.正方体的各顶点如图所示,正方体的三个面所在平面 ,分别记作 ,试用适当的符号填空.
∈
∈
∈
∈
∈
∈
∩
∩
∩
∩
∩
如果直线 l 与平面α有一个公共点P,直线 l 是否在平面α内?
平面公理
实际生活中,我们有这样的经验:把一根直尺边缘上的任意两点放到桌面上,可以看到,直尺的整个边缘就落在了桌面上.
如果直线 l 与平面α有两个公共点,直线 l 是否在平面α内?
平面公理
公理1 如果一条直线上的两点在一个平面内,那么这条直线在此平面内.
A
B
l
作用:
判定直线是否在平面内.
在生产、生活中,人们经过长期观察与实践,总结出关于平面的一些基本性质,我们把它作为公理.这些公理是进一步推理的基础.
平面公理
生活中经常看到用三角架支撑照相机.
平面公理
公理2 过不在一条直线上的三点,有且只有一个平面.
A
C
B
存在性
唯一性
作用:
确定平面的主要依据.
不在一条直线上的三个点A、B、C所确定的平面,可以记成“平面ABC”.
平面公理
推论2 经过两条相交直线,有且只有一个平面
推论3 经过两条平行直线,有且只有一个平面
推论1? 经过一条直线和这条直线外的一点,有
且只有一个平面
重要推论
把三角板的一个角立在课桌面上,三角板所在平面与桌面所在平面是否只相交于一点B?为什么?
B
平面公理
B
把三角板的一个角立在课桌面上,三角板所在平面与桌面所在平面是否只相交于一点B?为什么?
平面公理
观察长方体,你能发现长方体的两个相交平面有没有公共直线吗?
这条公共直线B’C’叫做这两个平面A’B’C’D’和平面BB’C’C的交线.
另一方面,相邻两个平面有一个公共点,如平面A’B’C’D’和平面BB’C’C有一个公共点B’,经过点B有且只有一条过该点的公共直线B’C’.
平面公理
公理3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
作用:
①判断两个平面相交的依据.
②判断点在直线上.
l
P
平面公理
例1 如图,用符号表示下列图形中点、直线、平面之间的位置关系.
a
l
A
B
a
l
P
b
(1)
(2)
解:在(1)中,
在(2)中,
典型例题
请叙述三条公理和三条推论
如果一条直线上的两点在一个平面内,那么这条直线在此平面内
过不在一条直线上的三点,有且只有一个平面
经过一条直线和这条直线外的一点有且只有一个平面
经过两条相交直线,有且只有一个平面
经过两条平行直线,有且只有一个平面
如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线
课堂练习:
P43页 1—4题
探究思考:
平面内一条直线把平面分成______部分
平面内两条直线可以把平面分成_________部分
平面内三条直线可以把平面分成_________部分
2
3或4
4或6或7
若三个平面两两相交有三条交线,若其中两条相交于一点,证明第三条交线也过这一点。
拓展练习
