高中数学人教A版必修2课件-2.2.3-2.2.4直线、平面与平面平行的性质(19张PPT)
文档属性
| 名称 | 高中数学人教A版必修2课件-2.2.3-2.2.4直线、平面与平面平行的性质(19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1011.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-12 22:23:51 | ||
图片预览


文档简介
2.2.3直线与平面平行的性质
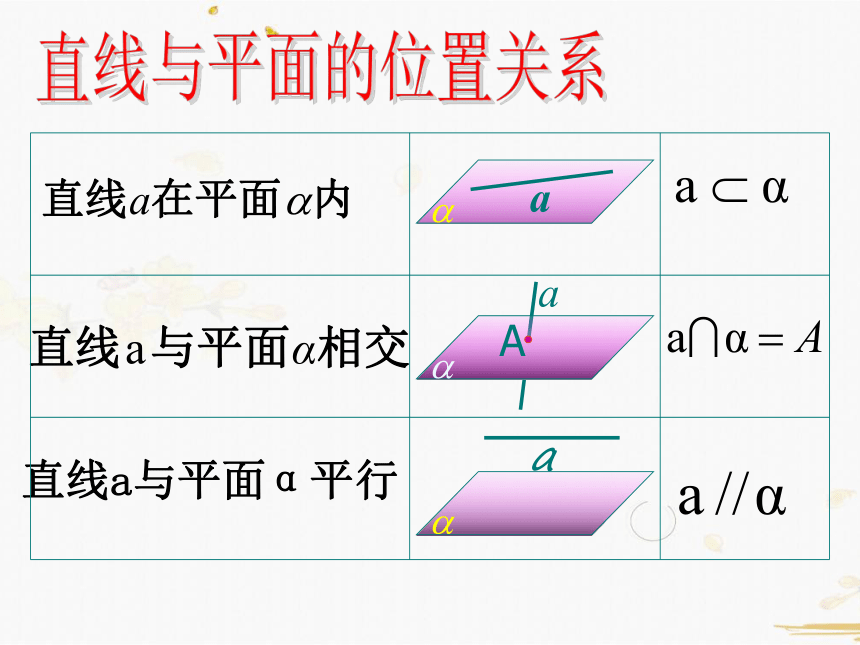
a
a
a
A
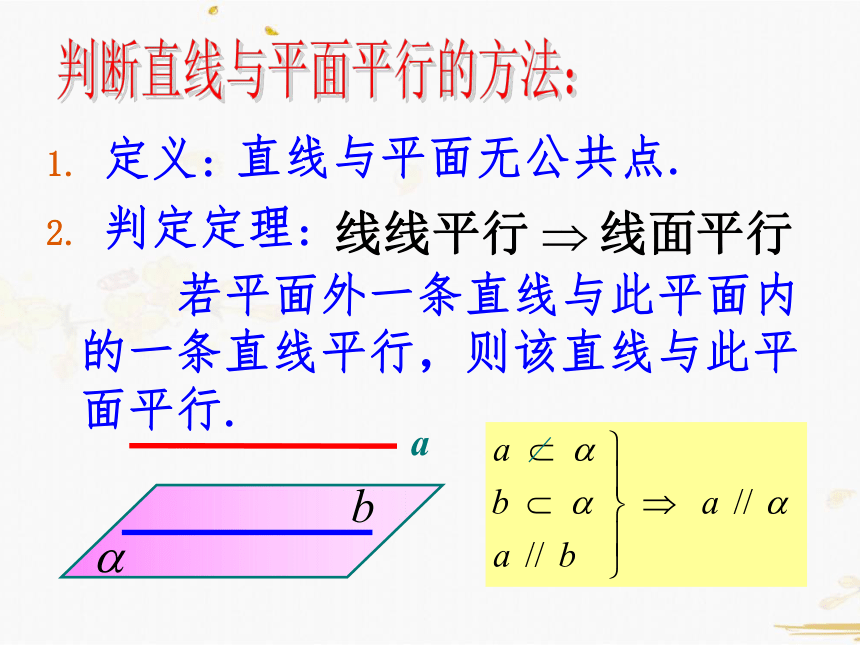
定义:
判定定理:
直线与平面无公共点.
若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
/
a
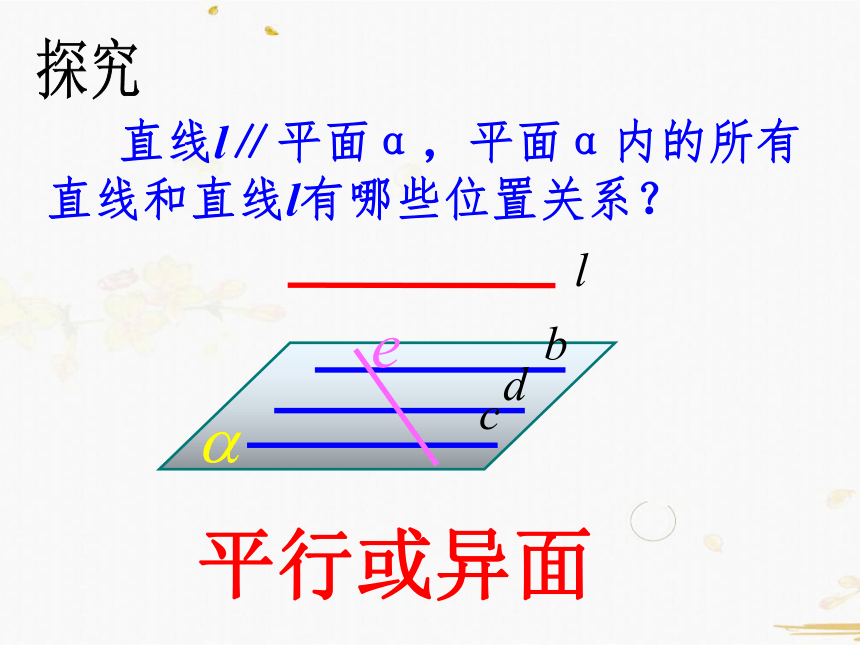
直线l∥平面α,平面α内的所有
直线和直线l有哪些位置关系?
平行或异面
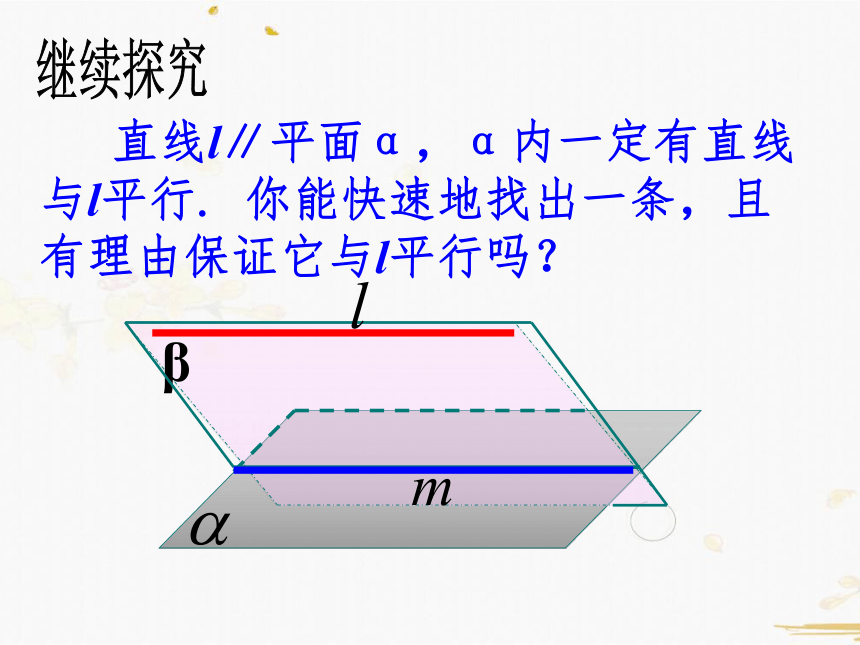
直线l∥平面α,α内一定有直线
与l平行. 你能快速地找出一条,且
有理由保证它与l平行吗?
β
探研新知
例1.已知:如图,a∥α,a??β,α∩β=b.
求证:a∥b.
证明:∵α∩β=b,
∴b?α, b? β
∵?a∥α
∴a与b无公共点
∵a?β,b?β
∴a∥b.
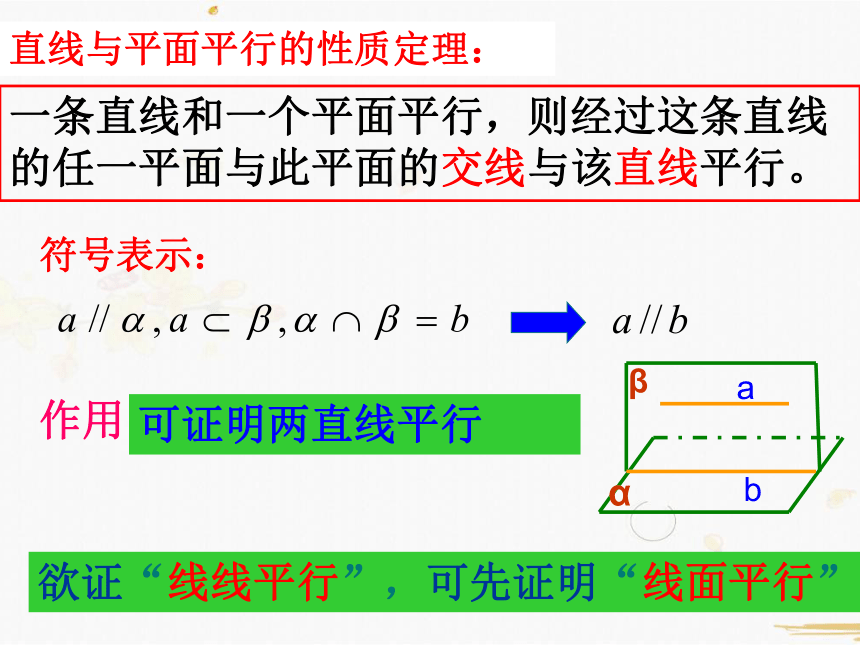
直线与平面平行的性质定理:
一条直线和一个平面平行,则经过这条直线的任一平面与此平面的交线与该直线平行。
a
b
α
β
符号表示:
作用:
可证明两直线平行
欲证“线线平行”,可先证明“线面平行”.
课堂练习:
以下命题(其中a,b表示直线,?表示平面)
①若a∥b,b??,则a∥?
②若a∥?,b∥?,则a∥b
③若a∥b,b∥?,则a∥?
④若a∥?,b??,则a∥b
其中正确命题的个数是 ( )
(A)0个 (B)1个 (C)2个 (D)3个
例1如图所示的一块木料中,棱BC平行于面A′C′.
(1)要经过面A′C′内一点P和棱BC
将木料锯开,应怎样画线?
(2)所画的线与平面AC是什么位置关系?
D′
例题讲解
A
B
C
D
A′
B′
C′
D′
E
F
P
例2、已知平面外的两条平行直线中的一条
平行于这个平面,
求证:另一条也平行于这个平面.
已知:直线a,b和平面α ,a∥b,a∥α , a,b都在平面α外 .
求证:b∥α .
b
a
c
2.2.4平面与平面平行的性质
定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
平面与平面平行判定定理
P
线面平行
面面平行
如果两个平面平行,那么一个平面内的直线与另一个平面具有什么位置关系?
思考:
a
平面与平面平行的性质1:
若两个平面平行,则一个平面内的直线必平行于另一个平面;
用符号如何表示呢?
简记为:面面平行→线面平行
如果两个平面平行,那么一个平面内的直线与另一个平面的直线具有什么位置关系?
思考:
a
如何在平面 内作出直线 a 的平行线呢?
a
b
α
β
平面与平面平行的性质定理2:
如果两个平行平面同时与第三个平面相交,那么它们的交线平行。
简记为:面面平行→线线平行
r
判定两直线平行的依据
例题分析
例1、求证:夹在两个平行平面间的两条平行线段相等
α
β
D
B
A
C
课堂练习
作业本:P62 第6题
书上:
1.课本P61 练习,A组第1题
2.练习册P33 例1+例2,P34 变式+当堂检测
3.复习:
必修5《全优课堂》 P36 变式1+变式2+变式3
小本P80 第17、20题
小结:
线
平行
线
线
平行
面
面
平行
面
线面平行判定
线面平行性质
面面平行判定
面面平行性质
2.三种平行关系的转化
1.面面平行性质定理:
如果两个平行平面同时与第三个平面相交,那么它们的交线平行。
已知:直线AB∥平面α,经过AB的两个平面β和γ分别和平面α交于直线a,b.
求证:a∥b
b
g
b
a
a
B
A
巩固练习
a
a
a
A
定义:
判定定理:
直线与平面无公共点.
若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
/
a
直线l∥平面α,平面α内的所有
直线和直线l有哪些位置关系?
平行或异面
直线l∥平面α,α内一定有直线
与l平行. 你能快速地找出一条,且
有理由保证它与l平行吗?
β
探研新知
例1.已知:如图,a∥α,a??β,α∩β=b.
求证:a∥b.
证明:∵α∩β=b,
∴b?α, b? β
∵?a∥α
∴a与b无公共点
∵a?β,b?β
∴a∥b.
直线与平面平行的性质定理:
一条直线和一个平面平行,则经过这条直线的任一平面与此平面的交线与该直线平行。
a
b
α
β
符号表示:
作用:
可证明两直线平行
欲证“线线平行”,可先证明“线面平行”.
课堂练习:
以下命题(其中a,b表示直线,?表示平面)
①若a∥b,b??,则a∥?
②若a∥?,b∥?,则a∥b
③若a∥b,b∥?,则a∥?
④若a∥?,b??,则a∥b
其中正确命题的个数是 ( )
(A)0个 (B)1个 (C)2个 (D)3个
例1如图所示的一块木料中,棱BC平行于面A′C′.
(1)要经过面A′C′内一点P和棱BC
将木料锯开,应怎样画线?
(2)所画的线与平面AC是什么位置关系?
D′
例题讲解
A
B
C
D
A′
B′
C′
D′
E
F
P
例2、已知平面外的两条平行直线中的一条
平行于这个平面,
求证:另一条也平行于这个平面.
已知:直线a,b和平面α ,a∥b,a∥α , a,b都在平面α外 .
求证:b∥α .
b
a
c
2.2.4平面与平面平行的性质
定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
平面与平面平行判定定理
P
线面平行
面面平行
如果两个平面平行,那么一个平面内的直线与另一个平面具有什么位置关系?
思考:
a
平面与平面平行的性质1:
若两个平面平行,则一个平面内的直线必平行于另一个平面;
用符号如何表示呢?
简记为:面面平行→线面平行
如果两个平面平行,那么一个平面内的直线与另一个平面的直线具有什么位置关系?
思考:
a
如何在平面 内作出直线 a 的平行线呢?
a
b
α
β
平面与平面平行的性质定理2:
如果两个平行平面同时与第三个平面相交,那么它们的交线平行。
简记为:面面平行→线线平行
r
判定两直线平行的依据
例题分析
例1、求证:夹在两个平行平面间的两条平行线段相等
α
β
D
B
A
C
课堂练习
作业本:P62 第6题
书上:
1.课本P61 练习,A组第1题
2.练习册P33 例1+例2,P34 变式+当堂检测
3.复习:
必修5《全优课堂》 P36 变式1+变式2+变式3
小本P80 第17、20题
小结:
线
平行
线
线
平行
面
面
平行
面
线面平行判定
线面平行性质
面面平行判定
面面平行性质
2.三种平行关系的转化
1.面面平行性质定理:
如果两个平行平面同时与第三个平面相交,那么它们的交线平行。
已知:直线AB∥平面α,经过AB的两个平面β和γ分别和平面α交于直线a,b.
求证:a∥b
b
g
b
a
a
B
A
巩固练习
