高中数学人教A版必修2课件-2.3.1直线与平面垂直的判定(2课时)(33张PPT)
文档属性
| 名称 | 高中数学人教A版必修2课件-2.3.1直线与平面垂直的判定(2课时)(33张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-12 00:00:00 | ||
图片预览










文档简介
引入新课
在直线和平面相交的位置关系中,有一种相交是很特殊的,我们把它叫做垂直相交,这节课我们重点来探究这种形式的相交。
观察实例,发现新知
旗杆与地面的关系,给人以直线与平面垂直的形象。
观察实例,发现新知
房屋的屋柱与地面的关系,给人以直线与平面垂直的形象。
大漠孤烟直
直线与平面垂直的定义:
如果一条直线l 和一个平面α内的任意一条直线都垂直,我们就说直线l 和平面α互相垂直.
记作:l ⊥α
α
l
P
l 叫做α的垂线, α叫做l 的垂面,
l 与α的唯一公共点P叫做垂足。
画直线与平面垂直时,通常把直线画成与表示平面的平行四边形的一边垂直。
如果一条直线垂直于一个平面内的无数条直线,那么这条直线是否与这个平面垂直?
不一定
如果一条直线与平面垂直,那么这条直线与这个面内的直线有何关系呢?
线面垂直的基本的性质
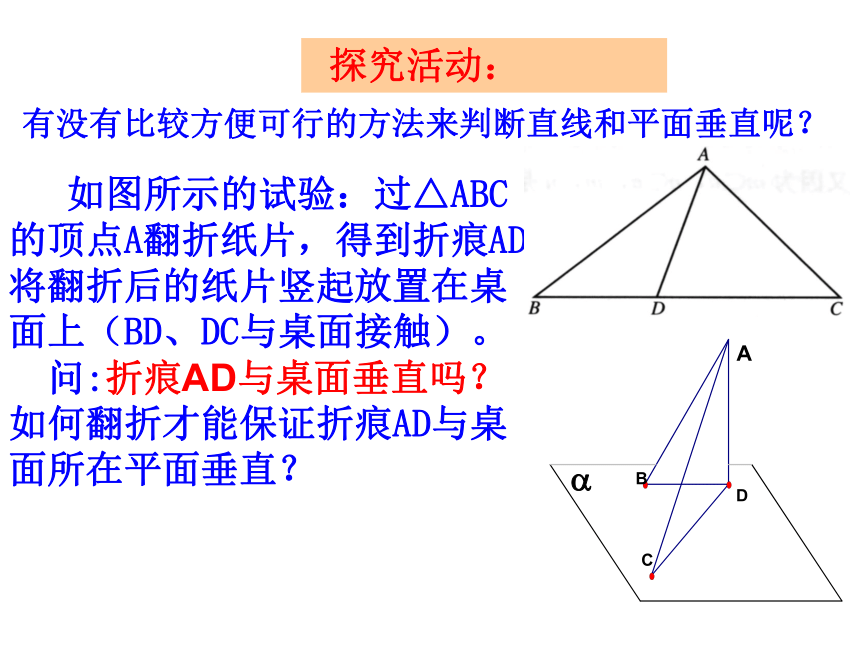
有没有比较方便可行的方法来判断直线和平面垂直呢?
如图所示的试验:过△ABC的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD、DC与桌面接触)。
问:折痕AD与桌面垂直吗?如何翻折才能保证折痕AD与桌面所在平面垂直?
A
探究活动:
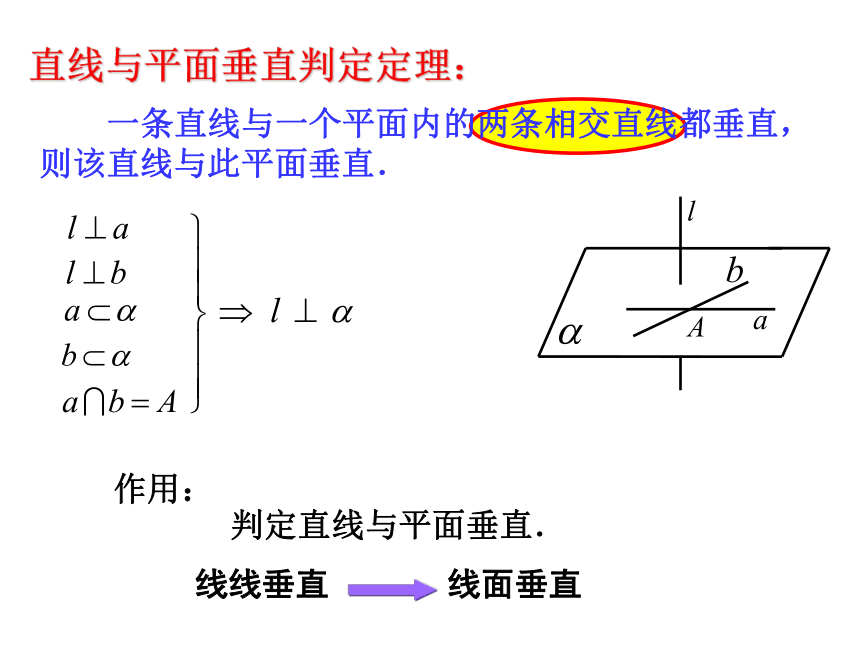
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.
作用:
判定直线与平面垂直.
直线与平面垂直判定定理:
线线垂直 线面垂直
例1 如图,已知 ,求证
根据直线与平面垂直的定义知
又因为
所以
又
是两条相交直线,
所以
证明:在平面 内作
两条相交直线m,n.
因为直线 ,
典型例题
P
A
B
C
O
2、如图,圆O所在一平面为 ,AB是圆O 的直径,C 是圆周上一点,且PA AC, PA AB,求证:
(1)PA BC
(2)BC 平面PAC
(2)
3.平行四边形ABCD所在平面a外有一点P,且PA=PB=PC=PD,求证:点P与平行四边形对角线交点O的连线PO垂直于AB、AD.
C
A
B
D
O
P
P
A
B
C
P67 :练习第2题
?
作业布置
做在作业本上
1.P67:练习第1题
2.P74:B组2题(写出证明)
做在书上
《优化设计》P38-P39 探究一、探究二
1、线面垂直,则线线垂直
2、线线垂直,则线面垂直
复习回顾
P
A
B
C
P67 :练习第2题
引入新课
我们知道,当直线和平面垂直时,该直线叫做平面的垂线。如果直线和平面不垂直,是不是也该给它取个名字呢?此时又该如何刻画直线和平面的这种关系呢?
如图,若一条直线PA和一个平面α相交,但不垂直,那么这条直线就叫做这个平面的斜线,斜线和平面的交点A叫做斜足。
P
A
斜足
斜线
斜交
P
A
O
直线和平面所成的角:
如图所示,一条直线PA和平面 相交,但不垂直,这
条直线叫这个平面的斜线,斜线和平面的交点A叫做斜足。
过斜线上斜足以外的一点P向平面引垂线PO ,过垂足O
和斜足A的直线AO叫做斜线在这个平面上的射影。
斜线和射影所成的锐角叫做这条直线和平面所成的角。
斜线
斜足
射影
如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
A1
D1
C1
B1
A
D
C
B
试一试
如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
A1
D1
C1
B1
A
D
C
B
O
线段B1O
试一试
如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
A1
D1
C1
B1
A
D
C
B
E
线段B1E
试一试
A1
B1
C1
D1
A
B
C
D
例1、如图,正方体ABCD-A1B1C1D1中,求
(1)直线A1B和平面 BCC1B1所成的角。
(2)直线A1B和平面A1B1CD所成的角。
O
例题示范,巩固新知
分析:找出直线A1B在平面BCC1B1和平面A1B1CD内的射影,就可
以求出A1B和平面BCC1B1和平面A1B1CD所成的角。
阅读教科书P67上的解答过程
步骤小结:一作二证三计算
如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角
A1
D1
C1
B1
A
D
C
B
0o
巩固练习
如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角
A1
D1
C1
B1
A
D
C
B
90o
巩固练习
如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角
A1
D1
C1
B1
A
D
C
B
45o
巩固练习
如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角
A1
D1
C1
B1
A
D
C
B
E
30o
巩固练习
作业布置
做在作业本上:
P74??B组4题
做在书上:
《优化设计》P39 探究三 典例
当堂检测
归纳小结
1.直线与平面垂直的概念
(1)利用定义;
(2)利用判定定理.
3.数学思想方法:转化的思想
空间问题
平面问题
3.直线与平面垂直的判定
线线垂直
线面垂直
垂直于平面内任意一条直线
2. 线面角的概念及范围
在直线和平面相交的位置关系中,有一种相交是很特殊的,我们把它叫做垂直相交,这节课我们重点来探究这种形式的相交。
观察实例,发现新知
旗杆与地面的关系,给人以直线与平面垂直的形象。
观察实例,发现新知
房屋的屋柱与地面的关系,给人以直线与平面垂直的形象。
大漠孤烟直
直线与平面垂直的定义:
如果一条直线l 和一个平面α内的任意一条直线都垂直,我们就说直线l 和平面α互相垂直.
记作:l ⊥α
α
l
P
l 叫做α的垂线, α叫做l 的垂面,
l 与α的唯一公共点P叫做垂足。
画直线与平面垂直时,通常把直线画成与表示平面的平行四边形的一边垂直。
如果一条直线垂直于一个平面内的无数条直线,那么这条直线是否与这个平面垂直?
不一定
如果一条直线与平面垂直,那么这条直线与这个面内的直线有何关系呢?
线面垂直的基本的性质
有没有比较方便可行的方法来判断直线和平面垂直呢?
如图所示的试验:过△ABC的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD、DC与桌面接触)。
问:折痕AD与桌面垂直吗?如何翻折才能保证折痕AD与桌面所在平面垂直?
A
探究活动:
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.
作用:
判定直线与平面垂直.
直线与平面垂直判定定理:
线线垂直 线面垂直
例1 如图,已知 ,求证
根据直线与平面垂直的定义知
又因为
所以
又
是两条相交直线,
所以
证明:在平面 内作
两条相交直线m,n.
因为直线 ,
典型例题
P
A
B
C
O
2、如图,圆O所在一平面为 ,AB是圆O 的直径,C 是圆周上一点,且PA AC, PA AB,求证:
(1)PA BC
(2)BC 平面PAC
(2)
3.平行四边形ABCD所在平面a外有一点P,且PA=PB=PC=PD,求证:点P与平行四边形对角线交点O的连线PO垂直于AB、AD.
C
A
B
D
O
P
P
A
B
C
P67 :练习第2题
?
作业布置
做在作业本上
1.P67:练习第1题
2.P74:B组2题(写出证明)
做在书上
《优化设计》P38-P39 探究一、探究二
1、线面垂直,则线线垂直
2、线线垂直,则线面垂直
复习回顾
P
A
B
C
P67 :练习第2题
引入新课
我们知道,当直线和平面垂直时,该直线叫做平面的垂线。如果直线和平面不垂直,是不是也该给它取个名字呢?此时又该如何刻画直线和平面的这种关系呢?
如图,若一条直线PA和一个平面α相交,但不垂直,那么这条直线就叫做这个平面的斜线,斜线和平面的交点A叫做斜足。
P
A
斜足
斜线
斜交
P
A
O
直线和平面所成的角:
如图所示,一条直线PA和平面 相交,但不垂直,这
条直线叫这个平面的斜线,斜线和平面的交点A叫做斜足。
过斜线上斜足以外的一点P向平面引垂线PO ,过垂足O
和斜足A的直线AO叫做斜线在这个平面上的射影。
斜线和射影所成的锐角叫做这条直线和平面所成的角。
斜线
斜足
射影
如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
A1
D1
C1
B1
A
D
C
B
试一试
如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
A1
D1
C1
B1
A
D
C
B
O
线段B1O
试一试
如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
A1
D1
C1
B1
A
D
C
B
E
线段B1E
试一试
A1
B1
C1
D1
A
B
C
D
例1、如图,正方体ABCD-A1B1C1D1中,求
(1)直线A1B和平面 BCC1B1所成的角。
(2)直线A1B和平面A1B1CD所成的角。
O
例题示范,巩固新知
分析:找出直线A1B在平面BCC1B1和平面A1B1CD内的射影,就可
以求出A1B和平面BCC1B1和平面A1B1CD所成的角。
阅读教科书P67上的解答过程
步骤小结:一作二证三计算
如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角
A1
D1
C1
B1
A
D
C
B
0o
巩固练习
如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角
A1
D1
C1
B1
A
D
C
B
90o
巩固练习
如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角
A1
D1
C1
B1
A
D
C
B
45o
巩固练习
如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角
A1
D1
C1
B1
A
D
C
B
E
30o
巩固练习
作业布置
做在作业本上:
P74??B组4题
做在书上:
《优化设计》P39 探究三 典例
当堂检测
归纳小结
1.直线与平面垂直的概念
(1)利用定义;
(2)利用判定定理.
3.数学思想方法:转化的思想
空间问题
平面问题
3.直线与平面垂直的判定
线线垂直
线面垂直
垂直于平面内任意一条直线
2. 线面角的概念及范围
