高中数学人教A版必修2课件-3.1.1斜率与倾斜角(15张PPT)
文档属性
| 名称 | 高中数学人教A版必修2课件-3.1.1斜率与倾斜角(15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 819.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-12 22:29:05 | ||
图片预览





文档简介
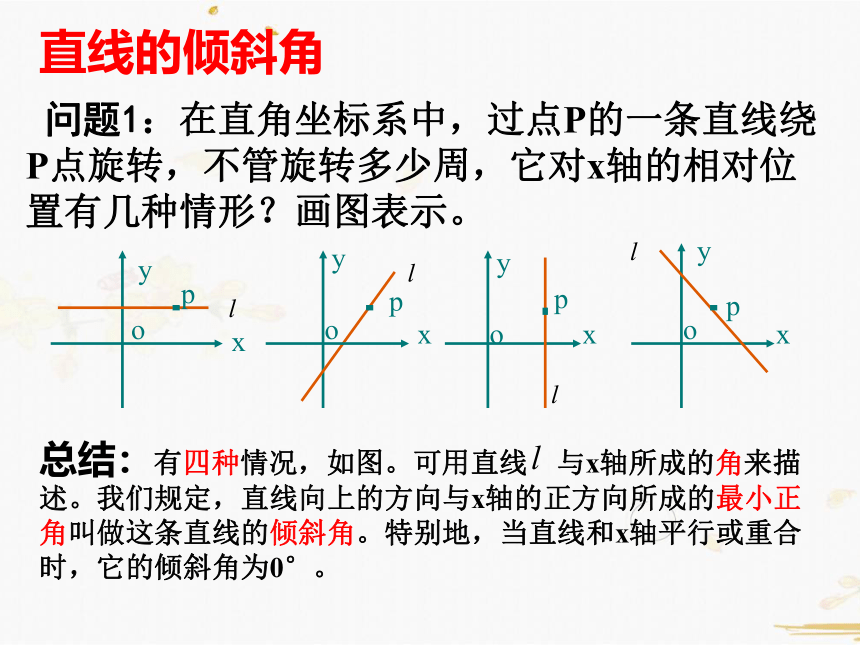
直线的倾斜角
问题1:在直角坐标系中,过点P的一条直线绕P点旋转,不管旋转多少周,它对x轴的相对位置有几种情形?画图表示。
总结:有四种情况,如图。可用直线 与x轴所成的角来描述。我们规定,直线向上的方向与x轴的正方向所成的最小正角叫做这条直线的倾斜角。特别地,当直线和x轴平行或重合时,它的倾斜角为0°。
p
o
y
x
y
p
o
x
p
o
y
x
p
o
y
x
定义:在平面直角坐标系中,对于一条与x轴相交的直线,如果把x轴(正方向)绕着交点按逆时针方向旋转到与直线重合时所转的最小正角 ,记为 ,那么就叫做直线的倾斜角。
a
也可以理解为:
直线向上的方向与X轴的正方向所夹的角。
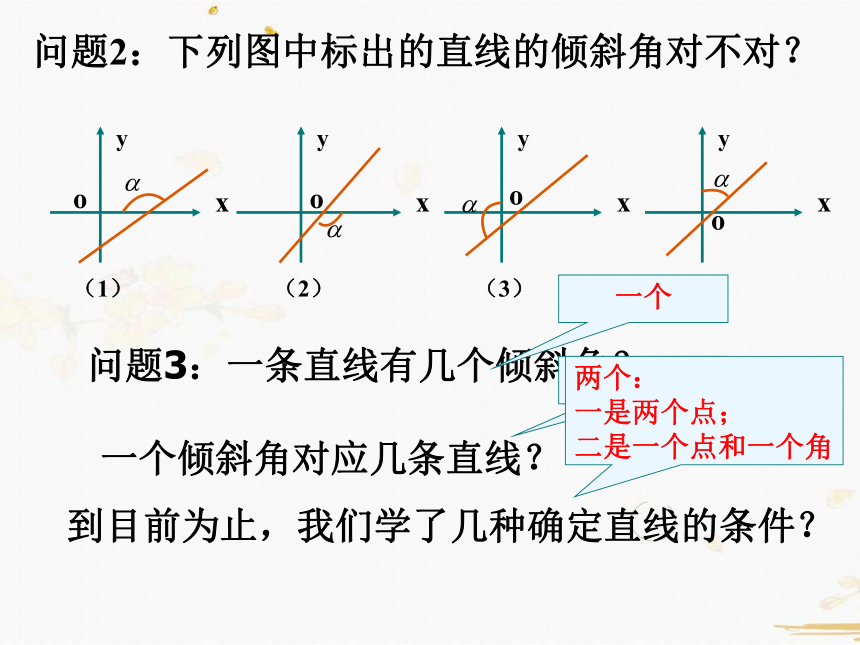
问题2:下列图中标出的直线的倾斜角对不对?
x
y
o
x
y
o
x
y
o
x
y
o
(1)
(2)
(3)
(4)
问题3:一条直线有几个倾斜角?
一个倾斜角对应几条直线?
到目前为止,我们学了几种确定直线的条件?
一个
无数条
两个:
一是两个点;
二是一个点和一个角
直线倾斜角的取值范围是:
0°≤ <180°
在此范围内,坐标平面上的任何一条直线都有唯一的倾斜角。而每一个倾斜角都能确定一条直线的方向,倾斜角直观地表示了直线对x轴正方向的倾斜程度。
通常用小写字母k表示,即
一条直线的倾斜角 的正切值叫做这条直线的斜率.
直线的斜率——直线的倾斜程度
如:倾斜角 时,直线的斜率
如:倾斜角为 时,由
当 为锐角时,
直线的斜率
倾斜角是 的直线有斜率吗?
倾斜角是 的直线的斜率不存在.
问:当 =0°时,k值如何?
当0°< < 90°时,k值如何?
当 =90°时,k值如何?
当90° < <180°时,k值如何?
直线的倾斜角与斜率k之间的关系:
的大小
0°
0°~90°
90°
90-180°
K的范围
0
(0,+∞)
不存在
(-∞,0)
K的增减性
—
随角递增而增大
——
随角递增而增大
下列哪些说法是正确的( )
A 、任一条直线都有倾斜角,也都有斜率
B、直线的倾斜角越大,斜率也越大
C 、平行于x轴的直线的倾斜角是0或π
D 、两直线的倾斜角相等,它们的斜率也相等
E 、两直线的斜率相等,它们的倾斜角也相等
F 、直线斜率的范围是R
E、F
练习:P86 第1题
如果不知道直线的倾斜角,但已知直线上两点的坐标,如何计算直线的斜率?即:给定两点P1 ( x1 ,y1), P2 ( x2 ,y2),并且x1 ≠x2,如何计算直线P1 P2的斜率k.
当 为锐角时,
在直角 中
斜率公式
公式的特点:
(1)与两点的顺序无关;
(2) 公式表明,直线对于x轴的倾斜度,可以通过直线上任意两点的坐标来表示,而不需要求出直线的倾斜角;
(3)当x1=x2时,公式不适用,此时直线与x轴垂直,α=900
例1 如图 ,已知 ,求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
解:直线AB的斜率
直线BC的斜率
直线CA的斜率
由 及 知,直线AB 与CA的倾斜角均为锐角;由 知,直线BC的倾斜角为钝角.
典型例题
例2 在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2及-3的直线 及 .
即
解:取 上某一点为 的坐标是 ,根据斜率公式有:
设 ,则 ,于是 的坐标是 .过原点及 的直线即为 .
x
y
是过原点及 的直线, 是过原点及
的直线, 是过原点及 的直线.
典型例题
练习:P86 第2、3、4题
作业布置:
P89 A组 第1——5题
两点间斜率公式
知识小结
倾斜角
斜率
问题1:在直角坐标系中,过点P的一条直线绕P点旋转,不管旋转多少周,它对x轴的相对位置有几种情形?画图表示。
总结:有四种情况,如图。可用直线 与x轴所成的角来描述。我们规定,直线向上的方向与x轴的正方向所成的最小正角叫做这条直线的倾斜角。特别地,当直线和x轴平行或重合时,它的倾斜角为0°。
p
o
y
x
y
p
o
x
p
o
y
x
p
o
y
x
定义:在平面直角坐标系中,对于一条与x轴相交的直线,如果把x轴(正方向)绕着交点按逆时针方向旋转到与直线重合时所转的最小正角 ,记为 ,那么就叫做直线的倾斜角。
a
也可以理解为:
直线向上的方向与X轴的正方向所夹的角。
问题2:下列图中标出的直线的倾斜角对不对?
x
y
o
x
y
o
x
y
o
x
y
o
(1)
(2)
(3)
(4)
问题3:一条直线有几个倾斜角?
一个倾斜角对应几条直线?
到目前为止,我们学了几种确定直线的条件?
一个
无数条
两个:
一是两个点;
二是一个点和一个角
直线倾斜角的取值范围是:
0°≤ <180°
在此范围内,坐标平面上的任何一条直线都有唯一的倾斜角。而每一个倾斜角都能确定一条直线的方向,倾斜角直观地表示了直线对x轴正方向的倾斜程度。
通常用小写字母k表示,即
一条直线的倾斜角 的正切值叫做这条直线的斜率.
直线的斜率——直线的倾斜程度
如:倾斜角 时,直线的斜率
如:倾斜角为 时,由
当 为锐角时,
直线的斜率
倾斜角是 的直线有斜率吗?
倾斜角是 的直线的斜率不存在.
问:当 =0°时,k值如何?
当0°< < 90°时,k值如何?
当 =90°时,k值如何?
当90° < <180°时,k值如何?
直线的倾斜角与斜率k之间的关系:
的大小
0°
0°~90°
90°
90-180°
K的范围
0
(0,+∞)
不存在
(-∞,0)
K的增减性
—
随角递增而增大
——
随角递增而增大
下列哪些说法是正确的( )
A 、任一条直线都有倾斜角,也都有斜率
B、直线的倾斜角越大,斜率也越大
C 、平行于x轴的直线的倾斜角是0或π
D 、两直线的倾斜角相等,它们的斜率也相等
E 、两直线的斜率相等,它们的倾斜角也相等
F 、直线斜率的范围是R
E、F
练习:P86 第1题
如果不知道直线的倾斜角,但已知直线上两点的坐标,如何计算直线的斜率?即:给定两点P1 ( x1 ,y1), P2 ( x2 ,y2),并且x1 ≠x2,如何计算直线P1 P2的斜率k.
当 为锐角时,
在直角 中
斜率公式
公式的特点:
(1)与两点的顺序无关;
(2) 公式表明,直线对于x轴的倾斜度,可以通过直线上任意两点的坐标来表示,而不需要求出直线的倾斜角;
(3)当x1=x2时,公式不适用,此时直线与x轴垂直,α=900
例1 如图 ,已知 ,求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
解:直线AB的斜率
直线BC的斜率
直线CA的斜率
由 及 知,直线AB 与CA的倾斜角均为锐角;由 知,直线BC的倾斜角为钝角.
典型例题
例2 在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2及-3的直线 及 .
即
解:取 上某一点为 的坐标是 ,根据斜率公式有:
设 ,则 ,于是 的坐标是 .过原点及 的直线即为 .
x
y
是过原点及 的直线, 是过原点及
的直线, 是过原点及 的直线.
典型例题
练习:P86 第2、3、4题
作业布置:
P89 A组 第1——5题
两点间斜率公式
知识小结
倾斜角
斜率
