高中数学人教A版必修2课件-4.1.1圆的标准方程(17张PPT)
文档属性
| 名称 | 高中数学人教A版必修2课件-4.1.1圆的标准方程(17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 533.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-12 22:35:51 | ||
图片预览






文档简介
4.1.1圆的标准方程
圆的标准方程
圆的定义:
平面内到定点的距离等于定长的点的集合。
定点
定长
圆心
半径
·
r
C
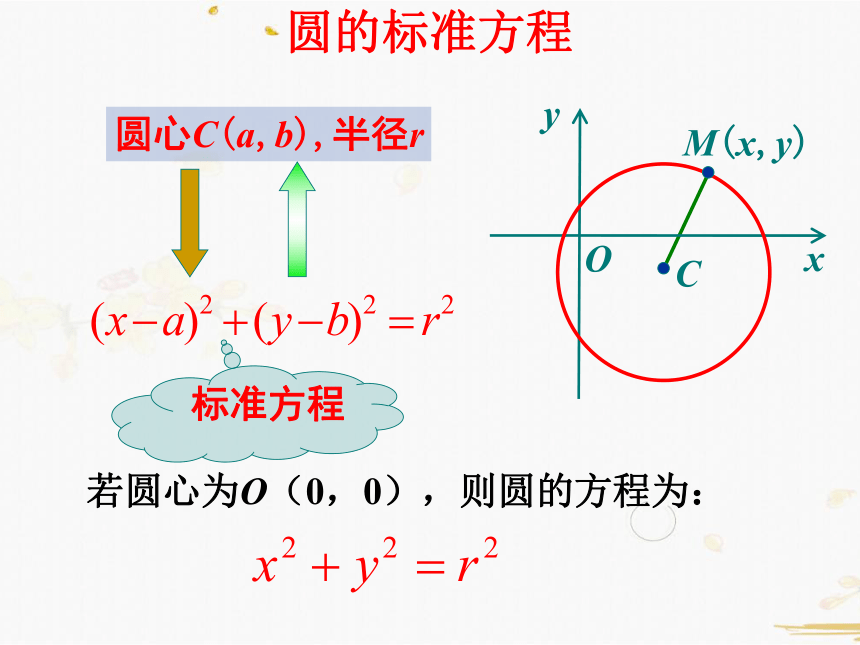
圆的标准方程
圆心是C(a,b),半径是r,求圆的方程.
x
y
O
C
M(x,y)
设点M (x,y)为圆C上任一点,
|MC|= r
则
P = { M | |MC| = r }
圆上所有点的集合
圆的标准方程
x
y
O
C
M(x,y)
圆心C(a,b),半径r
若圆心为O(0,0),则圆的方程为:
标准方程
圆心 (2, -4) ,半径
求圆心和半径
⑴圆 (x-1)2+ (y-1)2=9
⑵圆 (x-2)2+ (y+4)2=2
⑶圆 (x+1)2+ (y+2)2=m2
圆心 (1, 1) ,半径3
圆心 (-1, -2) ,半径|m|
P120 练习 1
P119 例1
若点到圆心的距离为d,
d>r时,点在圆外;
d=r时,点在圆上;
d(x0-a)2+(y0-b)2>r2时,点M在圆C外;
(x0-a)2+(y0-b)2=r2时,点M在圆C上;
(x0-a)2+(y0-b)2M
O
M
O
M
O
OMOM>r
OM=r
P121 练习 2
改为:
M1 (4 , -5 )
M2 (6 , 1 )
M3 (3 ,-6 )
P119 例2
待定系数法
解:设所求圆的方程为:
因为A(5,1),B (7,-3),C(2,8)都在圆上
所求圆的方程为
P120 例3
圆心:两条直线的交点
半径:圆心到圆上一点
x
y
O
C
A(1,1)
B(2,-2)
弦AB的垂直平分线
P120 例2 方法二
圆心:两条弦的中垂线的交点
半径:圆心到圆上一点
x
y
O
D
A(5,1)
B(7,-3)
C(2,-8)
P121 练习第3、4题
小结
圆心C(a,b),半径r
x
y
O
C
A
B
C
1.圆的标准方程
2.圆心
①两条直线的交点
(弦的垂直平分线)
②直径的中点
3.半径
①圆心到圆上一点
②圆心到切线的距离
作业布置
P124 A组 第2、3题
P121 练习 3
圆心:直径的中点
半径:直径的一半
解:设点C(a,b)为直径
的中点,则
圆方程为
因此点M在圆上,点N在圆外,点Q在圆内。
圆心坐标为 C(5,6)
补充例题:求以C(1,3)为圆心,并且和直线
3x-4y-7=0 相切的圆.
圆心:已知
半径:圆心到切线的距离
解:
设所求圆的半径为r
则:
=
∴所求圆的方程为:
C
y
x
O
M
圆的标准方程
圆的定义:
平面内到定点的距离等于定长的点的集合。
定点
定长
圆心
半径
·
r
C
圆的标准方程
圆心是C(a,b),半径是r,求圆的方程.
x
y
O
C
M(x,y)
设点M (x,y)为圆C上任一点,
|MC|= r
则
P = { M | |MC| = r }
圆上所有点的集合
圆的标准方程
x
y
O
C
M(x,y)
圆心C(a,b),半径r
若圆心为O(0,0),则圆的方程为:
标准方程
圆心 (2, -4) ,半径
求圆心和半径
⑴圆 (x-1)2+ (y-1)2=9
⑵圆 (x-2)2+ (y+4)2=2
⑶圆 (x+1)2+ (y+2)2=m2
圆心 (1, 1) ,半径3
圆心 (-1, -2) ,半径|m|
P120 练习 1
P119 例1
若点到圆心的距离为d,
d>r时,点在圆外;
d=r时,点在圆上;
d
(x0-a)2+(y0-b)2=r2时,点M在圆C上;
(x0-a)2+(y0-b)2
O
M
O
M
O
OM
OM=r
P121 练习 2
改为:
M1 (4 , -5 )
M2 (6 , 1 )
M3 (3 ,-6 )
P119 例2
待定系数法
解:设所求圆的方程为:
因为A(5,1),B (7,-3),C(2,8)都在圆上
所求圆的方程为
P120 例3
圆心:两条直线的交点
半径:圆心到圆上一点
x
y
O
C
A(1,1)
B(2,-2)
弦AB的垂直平分线
P120 例2 方法二
圆心:两条弦的中垂线的交点
半径:圆心到圆上一点
x
y
O
D
A(5,1)
B(7,-3)
C(2,-8)
P121 练习第3、4题
小结
圆心C(a,b),半径r
x
y
O
C
A
B
C
1.圆的标准方程
2.圆心
①两条直线的交点
(弦的垂直平分线)
②直径的中点
3.半径
①圆心到圆上一点
②圆心到切线的距离
作业布置
P124 A组 第2、3题
P121 练习 3
圆心:直径的中点
半径:直径的一半
解:设点C(a,b)为直径
的中点,则
圆方程为
因此点M在圆上,点N在圆外,点Q在圆内。
圆心坐标为 C(5,6)
补充例题:求以C(1,3)为圆心,并且和直线
3x-4y-7=0 相切的圆.
圆心:已知
半径:圆心到切线的距离
解:
设所求圆的半径为r
则:
=
∴所求圆的方程为:
C
y
x
O
M
