人教版 2020-2021学年八年级数学下册17.2 勾股定理与逆定理同步习题(Word版 含答案)
文档属性
| 名称 | 人教版 2020-2021学年八年级数学下册17.2 勾股定理与逆定理同步习题(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 289.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 00:00:00 | ||
图片预览



文档简介
勾股定理与逆定理
一、选择题
1.
以下列各组数据为三角形三边,能构成直角三角形的是(????)
A.
4?cm,8?cm,7?cm?????????????B.
2?cm,2?cm,2?cm?????????????
?C.
2?cm,2?cm,4?cm?????????????D.
13?cm,12?cm,5?cm?????????????
2.
若三角形三边长分别是6,8,10,则它最长边上的高为(????)
A.
6?????????????B.
4.8?????????????C.
2.4?????????????D.
8?????????????
3.
设的三边长分别为a、b、c,满足下列条件的中,不是直角三角形的是(????)
A.
?????????????
????
B.
?????????????
?C.
?????????????D.
a:b:c=3:4:6?????????????
4.
如图,某年的冰雪灾害中,一棵大树在离地面3米处折断,树的顶端落在树干底部4米处,那么这棵树折断之前的高度是(????)
?
A.
12米?????????????B.
8米?????????????C.
5米?????????????D.
5米或7米?????????????
5.
一消防员要爬上高12m的建筑物进行灭火抢险,为了安全,梯子底部距建筑物至少5m若梯子顶端恰好到达建筑物顶端,则梯子的长至少为(????)
A.
7m?????????????B.
12m?????????????C.
17m?????????????D.
13m?????????????
6.如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C'上,若AB=6,BC=9,则BF的长为 ( )
?
A.
4?????????????B.
3?????????????C.
4.5?????????????D.
5?????????????
二、填空题
7.
根据解直角三角形的知识回答下列问题:
?(1)在中,,a=5,b=12,则c=_____;
?(2)在中,,a=3,b=4,则c=_____;
?(3)在中,,,则_____.
8.
如图,在中,,AB=3cm,AC=5cm,将折叠,使点C与点A重合,得折痕DE,则的周长为____cm.
?
9.
如图,在中,,分别以BC,AB,AC为边向外作正方形,面积分别记为、、.若,,则____.
?
10.
阅读下面的解题过程:
?已知a、b、c为的三边,且满足,试判断的形状.
?解:∵,①
?∴,②
?∴,③
?∴是直角三角形.④
?回答下列问题:
?(1)上述解题过程是从____开始出现错误的;(填该步的代码)
?(2)错误的原因是:__________;
?(3)本题的正确结论是__________.
三、解答题
11.
已知中,AB=7,BC=24,AC=25,求的面积.
12.
已知点、,求、两点之间的距离.
13.
如图,在四边形ABCD中,已知AB∶BC∶CD∶DA=2∶2∶3∶1,且∠B=90°,试求∠DAB的度数.
?
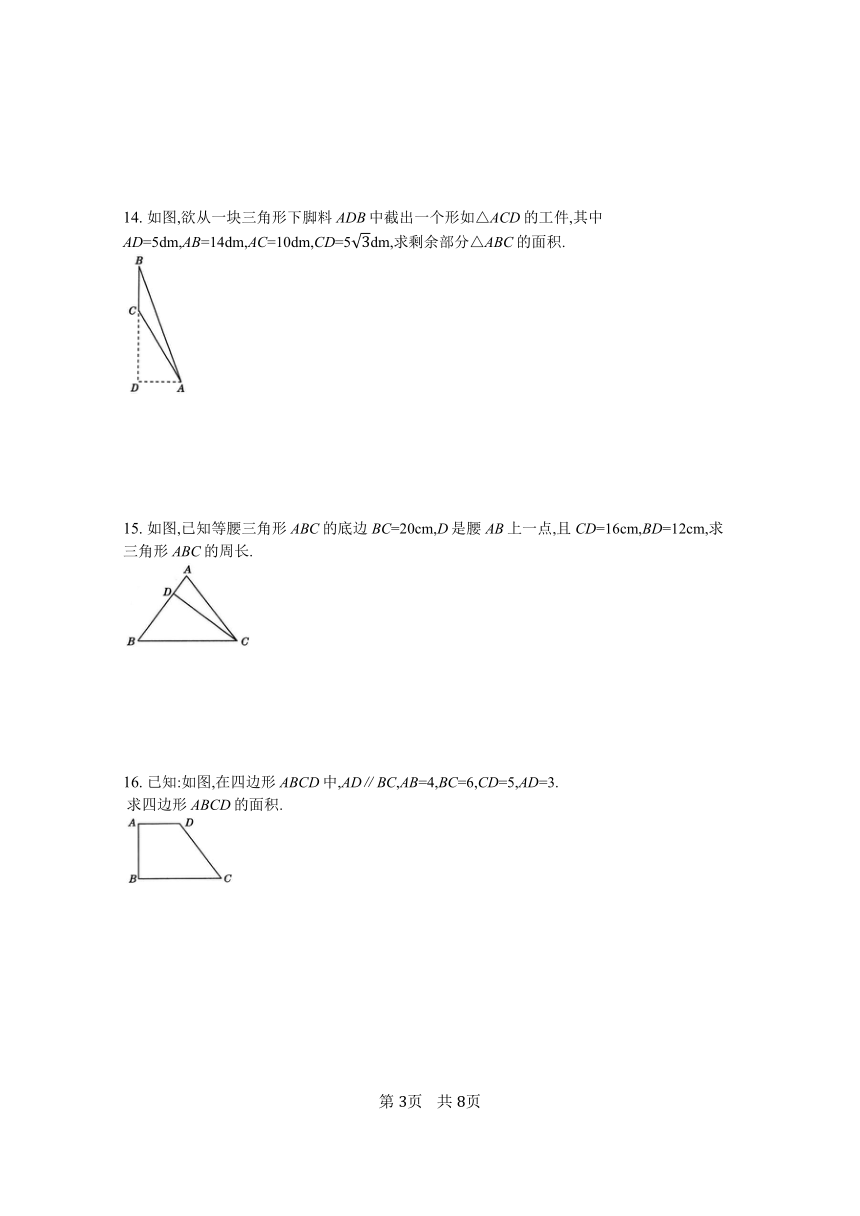
14.
如图,欲从一块三角形下脚料ADB中截出一个形如△ACD的工件,其中AD=5dm,AB=14dm,AC=10dm,CD=5dm,求剩余部分△ABC的面积.
?
15.
如图,已知等腰三角形ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm,求三角形ABC的周长.
?
16.
已知:如图,在四边形ABCD中,AD∥BC,AB=4,BC=6,CD=5,AD=3.
?求四边形ABCD的面积.
?
17.
如图所示的一块地,已知AD=4m,CD=3m,AD⊥DC,AB=13m,BC=12m,求这块地的面积.
?
18.
P为等边△ABC内部的一点,且PA=3,PB=4,PC=5,求∠APB的度数.
19.
已知:如图,在△ABC中,CD是AB边上的高,且CD2=AD·BD.
?求证:△ABC是直角三角形.
?
参考答案
1.
【答案】D【解析】根据勾股定理的逆定理知,D正确.
2.
【答案】B【解析】因为,由勾股定理的逆定理判断出该三角形是直角三角形,所以斜边上的高.
3.
【答案】D【解析】A项中,因为,所以;B项中,因为,所以;C项中,由角的大小比,可知,所以.因此前三个都是直角三角形,故选D.
4.
【答案】B【解析】由题意知是,所以由勾股定理得,即BC=5.∴树高=AC+BC=3+5=8(米).故选B.
5.
【答案】D【解析】梯子、墙和地面构成了一个直角三角形,则,∴梯子至少为13m.
6.
【答案】A【解析】本题考查图形折叠以及勾股定理,难度中等.
?由折叠知CF=C'F.设BF=x,CF=9-x,∴C'F=9-x,BC'=3.在Rt△C'BF中,由勾股定理可得C'F2=BF2+C'B2,即(9-x)2=x2+32,解得x=4,所以BF的长是4,故选A.
7.
【答案】(1)13;(2)?;?(3)112
?【解析】此类题目,应在直角三角形中先找准三角形的直角边和斜边,再利用勾股定理求解第三边的长,而特殊角的边则利用勾股定理中特殊角的边的关系进行求解.
8.
【答案】7
?【解析】在中,AB=3cm,AC=5cm,根据勾股定理,得BC=4cm.根据折叠的性质,得AE=EC,∴的周长为AB+BE+AE=AB+BE+EC=AB+BC=3+4=7(cm).
9.
【答案】2
?【解析】∵,∴由勾股定理得.又∵,,,∴,即.
10.
【答案】(1)③??(2)的值可能是0??(3)是等腰三角形或直角三角形
?【解析】依据等式的基本性质②:等式两边同时乘(或除)相等的非零的数或式子,两边依然相等。可知由②得出的结论应是或.
11.
【答案】,∴是以AC为斜边的直角三角形,∴.
?
12.
【答案】如图,过点作x轴的垂线,过点作y轴的垂线,设两条垂线交于点A,则∥y轴,∥x轴,∴.∵、,∴A(-2,-5),∴,,在Rt中,.即、两点之间的距离是10.
?
?
13.
【答案】连接AC.设DA=a,∵AB∶BC∶CD∶DA=2∶2∶3∶1,∴AB=2a,BC=2a,CD=3a.∵∠B=90°,AB=BC,∴∠BAC=45°.根据勾股定理,得AC2=AB2+BC2=8a2,∴AC2+AD2=8a2+a2=9a2=CD2,∴∠DAC=90°,∴∠DAB=∠DAC+∠BAC=90°+45°=135°.
?
14.
【答案】因为CD2+AD2=(5)2+52=100=AC2,
?所以△ACD是直角三角形,且∠D=90°.
?在Rt△ABD中,BD==3?(dm),所以BC=BD-CD=(3-5)?dm,?所以△ABC的面积为BC·AD=×(3-5)×5=(dm2).
?
15.
【答案】在△BCD中,BC=20?cm,CD=16?cm,BD=12?cm,
?∵BD2+DC2=BC2,
?∴△BCD是直角三角形,且∠BDC=90°.
?设AD=x?cm,则AC=AB=AD+DB=(x+12)?cm,
?在Rt△ADC中,∵AC2=AD2+DC2,
?∴(x+12)2=x2+162,
?解得x=.
?∴△ABC的周长为×2+20=?(cm).
?
16.
【答案】如图,作DE∥AB交BC于点E,连接BD,
?则可以证明△ABD≌△EDB(ASA),
?
?∴DE=AB=4,BE=AD=3.
?∵BC=6,∴EC=BC-BE=3,∴EC=EB.
?∵DE2+CE2=42+32=25=CD2,
?∴△DEC为直角三角形,∴∠DEC=90°.
?又∵EC=EB=3,
?∴△DBC为等腰三角形,∴DB=DC=5.
?在△BDA中,
?∵AD2+AB2=32+42=25=BD2,
?∴△BDA是直角三角形.
?易得S△BDA=×3×4=6,
?S△DBC=×6×4=12,
?∴S△四边形ABCD=S△BDA+S△DBC=6+12=18.
?
17.
【答案】连接AC(如图).
?
?∵AD⊥DC,
?∴在Rt△ACD中,由勾股定理
?得AC==5?m.
?又∵AC2+BC2=52+122=132=AB2,
?∴△ABC为直角三角形,
?∴这块地的面积为S△ABC-S△ACD=AC×BC-AD×CD=×?5×12-×4×?3=24(m2).
?
18.
【答案】如图所示,将△ABP绕点A逆时针旋转60°得到△ACM,连接AM,PM,CM,
?
?由题意知△ABP≌△ACM,
?其中∠APB=∠AMC,
?∴AP=AM=3,BP=CM=4,
?∠PAM=60°,
?∴△APM为等边三角形.
?∴∠AMP=60°,∴PM=AP=3.
?在△PCM中,PM2+CM2=32+42=25,PC2=52=25.
?∴PM2+CM2=PC2,∴∠PMC=90°.
?∴∠APB=∠AMC=∠AMP+∠PMC=60°+90°=150°.
?
19.
【答案】在Rt△ACD和Rt△BCD中,
?∵AC2=AD2+CD2,BC2=CD2+BD2,
?∴AC2+BC2=AD2+2CD2+BD2=AD2+2AD·BD+BD2=(AD+BD)2=AB2,
?∴△ABC是直角三角形.
?
第8页
共8页
第7页
共8页
一、选择题
1.
以下列各组数据为三角形三边,能构成直角三角形的是(????)
A.
4?cm,8?cm,7?cm?????????????B.
2?cm,2?cm,2?cm?????????????
?C.
2?cm,2?cm,4?cm?????????????D.
13?cm,12?cm,5?cm?????????????
2.
若三角形三边长分别是6,8,10,则它最长边上的高为(????)
A.
6?????????????B.
4.8?????????????C.
2.4?????????????D.
8?????????????
3.
设的三边长分别为a、b、c,满足下列条件的中,不是直角三角形的是(????)
A.
?????????????
????
B.
?????????????
?C.
?????????????D.
a:b:c=3:4:6?????????????
4.
如图,某年的冰雪灾害中,一棵大树在离地面3米处折断,树的顶端落在树干底部4米处,那么这棵树折断之前的高度是(????)
?
A.
12米?????????????B.
8米?????????????C.
5米?????????????D.
5米或7米?????????????
5.
一消防员要爬上高12m的建筑物进行灭火抢险,为了安全,梯子底部距建筑物至少5m若梯子顶端恰好到达建筑物顶端,则梯子的长至少为(????)
A.
7m?????????????B.
12m?????????????C.
17m?????????????D.
13m?????????????
6.如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C'上,若AB=6,BC=9,则BF的长为 ( )
?
A.
4?????????????B.
3?????????????C.
4.5?????????????D.
5?????????????
二、填空题
7.
根据解直角三角形的知识回答下列问题:
?(1)在中,,a=5,b=12,则c=_____;
?(2)在中,,a=3,b=4,则c=_____;
?(3)在中,,,则_____.
8.
如图,在中,,AB=3cm,AC=5cm,将折叠,使点C与点A重合,得折痕DE,则的周长为____cm.
?
9.
如图,在中,,分别以BC,AB,AC为边向外作正方形,面积分别记为、、.若,,则____.
?
10.
阅读下面的解题过程:
?已知a、b、c为的三边,且满足,试判断的形状.
?解:∵,①
?∴,②
?∴,③
?∴是直角三角形.④
?回答下列问题:
?(1)上述解题过程是从____开始出现错误的;(填该步的代码)
?(2)错误的原因是:__________;
?(3)本题的正确结论是__________.
三、解答题
11.
已知中,AB=7,BC=24,AC=25,求的面积.
12.
已知点、,求、两点之间的距离.
13.
如图,在四边形ABCD中,已知AB∶BC∶CD∶DA=2∶2∶3∶1,且∠B=90°,试求∠DAB的度数.
?
14.
如图,欲从一块三角形下脚料ADB中截出一个形如△ACD的工件,其中AD=5dm,AB=14dm,AC=10dm,CD=5dm,求剩余部分△ABC的面积.
?
15.
如图,已知等腰三角形ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm,求三角形ABC的周长.
?
16.
已知:如图,在四边形ABCD中,AD∥BC,AB=4,BC=6,CD=5,AD=3.
?求四边形ABCD的面积.
?
17.
如图所示的一块地,已知AD=4m,CD=3m,AD⊥DC,AB=13m,BC=12m,求这块地的面积.
?
18.
P为等边△ABC内部的一点,且PA=3,PB=4,PC=5,求∠APB的度数.
19.
已知:如图,在△ABC中,CD是AB边上的高,且CD2=AD·BD.
?求证:△ABC是直角三角形.
?
参考答案
1.
【答案】D【解析】根据勾股定理的逆定理知,D正确.
2.
【答案】B【解析】因为,由勾股定理的逆定理判断出该三角形是直角三角形,所以斜边上的高.
3.
【答案】D【解析】A项中,因为,所以;B项中,因为,所以;C项中,由角的大小比,可知,所以.因此前三个都是直角三角形,故选D.
4.
【答案】B【解析】由题意知是,所以由勾股定理得,即BC=5.∴树高=AC+BC=3+5=8(米).故选B.
5.
【答案】D【解析】梯子、墙和地面构成了一个直角三角形,则,∴梯子至少为13m.
6.
【答案】A【解析】本题考查图形折叠以及勾股定理,难度中等.
?由折叠知CF=C'F.设BF=x,CF=9-x,∴C'F=9-x,BC'=3.在Rt△C'BF中,由勾股定理可得C'F2=BF2+C'B2,即(9-x)2=x2+32,解得x=4,所以BF的长是4,故选A.
7.
【答案】(1)13;(2)?;?(3)112
?【解析】此类题目,应在直角三角形中先找准三角形的直角边和斜边,再利用勾股定理求解第三边的长,而特殊角的边则利用勾股定理中特殊角的边的关系进行求解.
8.
【答案】7
?【解析】在中,AB=3cm,AC=5cm,根据勾股定理,得BC=4cm.根据折叠的性质,得AE=EC,∴的周长为AB+BE+AE=AB+BE+EC=AB+BC=3+4=7(cm).
9.
【答案】2
?【解析】∵,∴由勾股定理得.又∵,,,∴,即.
10.
【答案】(1)③??(2)的值可能是0??(3)是等腰三角形或直角三角形
?【解析】依据等式的基本性质②:等式两边同时乘(或除)相等的非零的数或式子,两边依然相等。可知由②得出的结论应是或.
11.
【答案】,∴是以AC为斜边的直角三角形,∴.
?
12.
【答案】如图,过点作x轴的垂线,过点作y轴的垂线,设两条垂线交于点A,则∥y轴,∥x轴,∴.∵、,∴A(-2,-5),∴,,在Rt中,.即、两点之间的距离是10.
?
?
13.
【答案】连接AC.设DA=a,∵AB∶BC∶CD∶DA=2∶2∶3∶1,∴AB=2a,BC=2a,CD=3a.∵∠B=90°,AB=BC,∴∠BAC=45°.根据勾股定理,得AC2=AB2+BC2=8a2,∴AC2+AD2=8a2+a2=9a2=CD2,∴∠DAC=90°,∴∠DAB=∠DAC+∠BAC=90°+45°=135°.
?
14.
【答案】因为CD2+AD2=(5)2+52=100=AC2,
?所以△ACD是直角三角形,且∠D=90°.
?在Rt△ABD中,BD==3?(dm),所以BC=BD-CD=(3-5)?dm,?所以△ABC的面积为BC·AD=×(3-5)×5=(dm2).
?
15.
【答案】在△BCD中,BC=20?cm,CD=16?cm,BD=12?cm,
?∵BD2+DC2=BC2,
?∴△BCD是直角三角形,且∠BDC=90°.
?设AD=x?cm,则AC=AB=AD+DB=(x+12)?cm,
?在Rt△ADC中,∵AC2=AD2+DC2,
?∴(x+12)2=x2+162,
?解得x=.
?∴△ABC的周长为×2+20=?(cm).
?
16.
【答案】如图,作DE∥AB交BC于点E,连接BD,
?则可以证明△ABD≌△EDB(ASA),
?
?∴DE=AB=4,BE=AD=3.
?∵BC=6,∴EC=BC-BE=3,∴EC=EB.
?∵DE2+CE2=42+32=25=CD2,
?∴△DEC为直角三角形,∴∠DEC=90°.
?又∵EC=EB=3,
?∴△DBC为等腰三角形,∴DB=DC=5.
?在△BDA中,
?∵AD2+AB2=32+42=25=BD2,
?∴△BDA是直角三角形.
?易得S△BDA=×3×4=6,
?S△DBC=×6×4=12,
?∴S△四边形ABCD=S△BDA+S△DBC=6+12=18.
?
17.
【答案】连接AC(如图).
?
?∵AD⊥DC,
?∴在Rt△ACD中,由勾股定理
?得AC==5?m.
?又∵AC2+BC2=52+122=132=AB2,
?∴△ABC为直角三角形,
?∴这块地的面积为S△ABC-S△ACD=AC×BC-AD×CD=×?5×12-×4×?3=24(m2).
?
18.
【答案】如图所示,将△ABP绕点A逆时针旋转60°得到△ACM,连接AM,PM,CM,
?
?由题意知△ABP≌△ACM,
?其中∠APB=∠AMC,
?∴AP=AM=3,BP=CM=4,
?∠PAM=60°,
?∴△APM为等边三角形.
?∴∠AMP=60°,∴PM=AP=3.
?在△PCM中,PM2+CM2=32+42=25,PC2=52=25.
?∴PM2+CM2=PC2,∴∠PMC=90°.
?∴∠APB=∠AMC=∠AMP+∠PMC=60°+90°=150°.
?
19.
【答案】在Rt△ACD和Rt△BCD中,
?∵AC2=AD2+CD2,BC2=CD2+BD2,
?∴AC2+BC2=AD2+2CD2+BD2=AD2+2AD·BD+BD2=(AD+BD)2=AB2,
?∴△ABC是直角三角形.
?
第8页
共8页
第7页
共8页
