《二元一次不等式(组)与简单的线性规划》同步检测卷(1)
文档属性
| 名称 | 《二元一次不等式(组)与简单的线性规划》同步检测卷(1) |
|
|
| 格式 | zip | ||
| 文件大小 | 65.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-11 00:00:00 | ||
图片预览


文档简介
《二元一次不等式(组)与简单的线性规划》同步检测卷(1)
(时间:90分钟,满分100分)
一、选择题:(每小题4分,共32分)
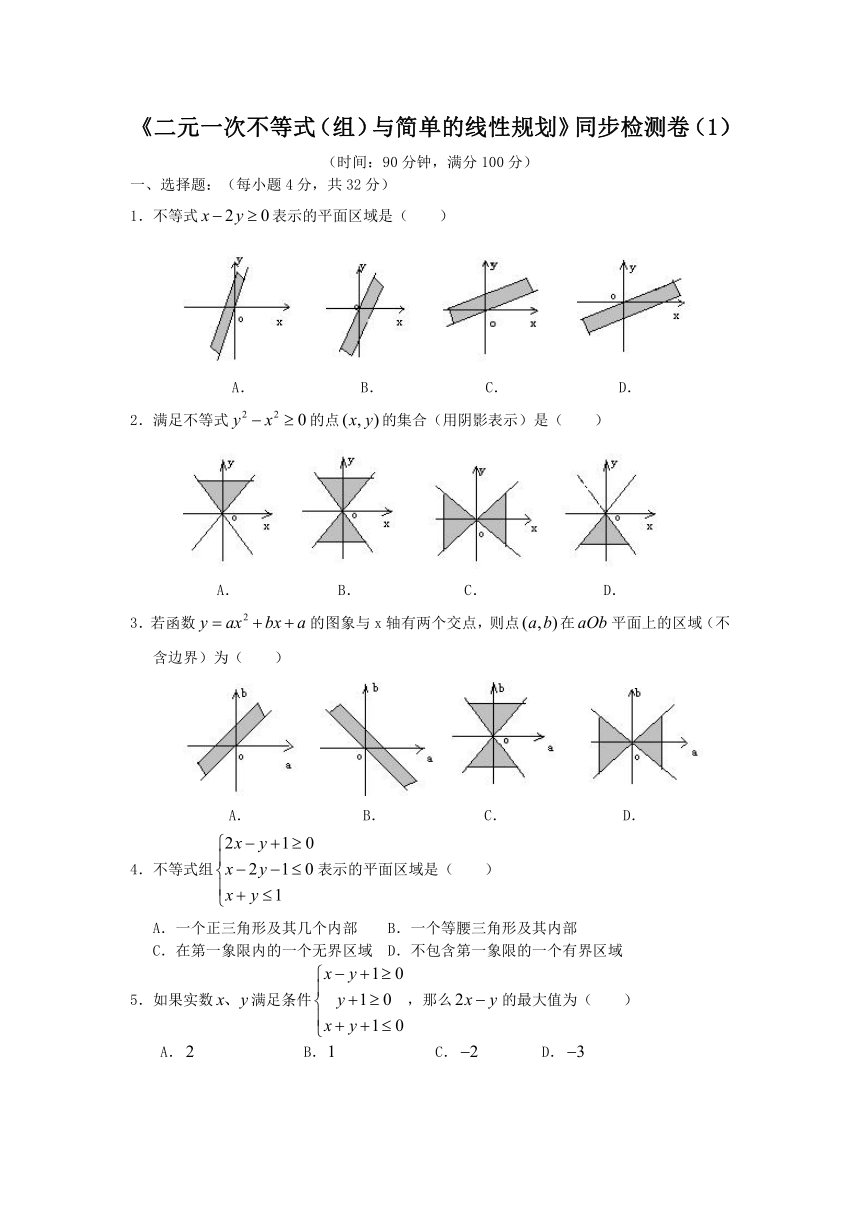
1.不等式表示的平面区域是( )
A. B. C. D.
2.满足不等式的点的集合(用阴影表示)是( )
A. B. C. D.
3.若函数的图象与x轴有两个交点,则点在平面上的区域(不含边界)为( )
A. B. C. D.
4.不等式组表示的平面区域是( )
A.一个正三角形及其几个内部 B.一个等腰三角形及其内部
C.在第一象限内的一个无界区域 D.不包含第一象限的一个有界区域
5.如果实数满足条件,那么的最大值为( )
A. B. C. D.
6.已知点P(x,y)在不等式组表示的平面区域上运动,则z=x-y的取值范围是( )
A.[-2,-1] B.[-2,1] C.[-1,2] D.[1,2]
7.在平面直角坐标系中,不等式组表示的平面区域的面积是( )
A.4 B.4 C.2 D.2
8.在约束条件下,当时,
目标函数的最大值的变化范围是( )
A. B. C. D.
二、填空题(每小题4分,共20分)
9.点到直线的距离为,且在表示的区域内,则_____
10.不等式组表示的区域中,坐标是整数的点共有_________个。
11.某实验室需购某种化工原料106千克,现在市场上该原料有两种包装,一种是每袋35千克,价格为140元;另一种是每袋24千克,价格为120元. 在满足需要的条件下,最少要花费 ___ 元.
12.设变量、满足约束条件,则目标函数的最小值为_______
13.已知点的坐标满足条件,点为坐标原点,那么的最小值等于_______,最大值等于____________.
三、解答题:(共48分)
16.某厂生产A与B两种产品,每公斤的产值分别为600元与400元.又知每生产1公斤A产品需要电力2千瓦、煤4吨;而生产1公斤B产品需要电力3千瓦、煤2吨.但该厂的电力供应不得超过100千瓦,煤最多只有120吨.问如何安排生产计划以取得最大产值
17.某运输队公司接受了向抗洪抢险地区每天至少运送180t支援物资的任务,该公司有8辆载重量为6t的A型卡车与4辆载重量为10t的B型卡车,有10名驾驶员。每辆卡车每天往返的次数为A型卡车4次,B型卡车3次。每辆卡车每天往返的成本费为A型车320元,B型车504元,请你给该公司调配车辆,使公司所花的成本最低
18.某公司准备进行两种组合投资,稳健型组合投资是由每份金融投资20万元,房地产投资30万元组成;进取型组合投资是由每份金融投资40万元,房地产投资30万元组成。已知每份稳健型组合投资每年可获利10万元,每份进取型组合投资每年可获利15万元。若可作投资用的资金中,金融投资不超过160万元,房地产投资不超过180万元,那么这两种组合投资应注入多少份,才能使一年获利总额最多?
A卷参考答案
一、选择题:1.D.2.B.3.C.4.B. 5. B. 6. C.7.B.8.D.
二、填空题:
9 、16或-4; 10. 10个; 11、500元 12.3 13.,.
8.由交点为,
(1)当时可行域是四边形OABC,此时,
(2)当时可行域是△OA此时,
故选D.
11.解:设需35千克袋,24千克袋,则目标函数元,约束条件为
,当时,,即,这时
三、解答题:
16.某厂生产A与B两种产品,每公斤的产值分别为600元与400元.又知每生产1公斤A产品需要电力2千瓦、煤4吨;而生产1公斤B产品需要电力3千瓦、煤2吨.但该厂的电力供应不得超过100千瓦,煤最多只有120吨.问如何安排生产计划以取得最大产值
解:设生产A与B两种产品分别为x公斤,y公斤,总产值为Z元。则
且
作可行域:
作直线l:600x+400y=0,即直线l:3x+2y=0,把直线l向右上方平移至l1的位置时,直线经过可行域上的点A,且与原点距离最大,此时z=600x+400y取最大值.解方程组
,得A的坐标为x=20,y=20
答:生产A产品20公斤、B产品20公斤才能才能使产值最大。
17.某运输队公司接受了向抗洪抢险地区每天至少运送180t支援物资的任务,该公司有8辆载重量为6t的A型卡车与4辆载重量为10t的B型卡车,有10名驾驶员。每辆卡车每天往返的次数为A型卡车4次,B型卡车3次。每辆卡车每天往返的成本费为A型车320元,B型车504元,请你给该公司调配车辆,使公司所花的成本最低
17.解:设每天调出A型车x辆,B型车y辆,公司所花的成本为z元,则有
且,由图解法可得最优整点解为(5,2),即每天调出A型车5辆,B型车2辆时,公司所花的成本最低。
18.某公司准备进行两种组合投资,稳健型组合投资是由每份金融投资20万元,房地产投资30万元组成;进取型组合投资是由每份金融投资40万元,房地产投资30万元组成。已知每份稳健型组合投资每年可获利10万元,每份进取型组合投资每年可获利15万元。若可作投资用的资金中,金融投资不超过160万元,房地产投资不超过180万元,那么这两种组合投资应注入多少份,才能使一年获利总额最多?
18.解:设稳健型投资份,进取型投资份,利润总额为(×10万元),
则目标函数为(×10万元),
线性约束条件为:,即
作出可行域(图略),解方程组,得交点
作直线,平移,当过点M时,取最大值:万元=70万元。
(时间:90分钟,满分100分)
一、选择题:(每小题4分,共32分)
1.不等式表示的平面区域是( )
A. B. C. D.
2.满足不等式的点的集合(用阴影表示)是( )
A. B. C. D.
3.若函数的图象与x轴有两个交点,则点在平面上的区域(不含边界)为( )
A. B. C. D.
4.不等式组表示的平面区域是( )
A.一个正三角形及其几个内部 B.一个等腰三角形及其内部
C.在第一象限内的一个无界区域 D.不包含第一象限的一个有界区域
5.如果实数满足条件,那么的最大值为( )
A. B. C. D.
6.已知点P(x,y)在不等式组表示的平面区域上运动,则z=x-y的取值范围是( )
A.[-2,-1] B.[-2,1] C.[-1,2] D.[1,2]
7.在平面直角坐标系中,不等式组表示的平面区域的面积是( )
A.4 B.4 C.2 D.2
8.在约束条件下,当时,
目标函数的最大值的变化范围是( )
A. B. C. D.
二、填空题(每小题4分,共20分)
9.点到直线的距离为,且在表示的区域内,则_____
10.不等式组表示的区域中,坐标是整数的点共有_________个。
11.某实验室需购某种化工原料106千克,现在市场上该原料有两种包装,一种是每袋35千克,价格为140元;另一种是每袋24千克,价格为120元. 在满足需要的条件下,最少要花费 ___ 元.
12.设变量、满足约束条件,则目标函数的最小值为_______
13.已知点的坐标满足条件,点为坐标原点,那么的最小值等于_______,最大值等于____________.
三、解答题:(共48分)
16.某厂生产A与B两种产品,每公斤的产值分别为600元与400元.又知每生产1公斤A产品需要电力2千瓦、煤4吨;而生产1公斤B产品需要电力3千瓦、煤2吨.但该厂的电力供应不得超过100千瓦,煤最多只有120吨.问如何安排生产计划以取得最大产值
17.某运输队公司接受了向抗洪抢险地区每天至少运送180t支援物资的任务,该公司有8辆载重量为6t的A型卡车与4辆载重量为10t的B型卡车,有10名驾驶员。每辆卡车每天往返的次数为A型卡车4次,B型卡车3次。每辆卡车每天往返的成本费为A型车320元,B型车504元,请你给该公司调配车辆,使公司所花的成本最低
18.某公司准备进行两种组合投资,稳健型组合投资是由每份金融投资20万元,房地产投资30万元组成;进取型组合投资是由每份金融投资40万元,房地产投资30万元组成。已知每份稳健型组合投资每年可获利10万元,每份进取型组合投资每年可获利15万元。若可作投资用的资金中,金融投资不超过160万元,房地产投资不超过180万元,那么这两种组合投资应注入多少份,才能使一年获利总额最多?
A卷参考答案
一、选择题:1.D.2.B.3.C.4.B. 5. B. 6. C.7.B.8.D.
二、填空题:
9 、16或-4; 10. 10个; 11、500元 12.3 13.,.
8.由交点为,
(1)当时可行域是四边形OABC,此时,
(2)当时可行域是△OA此时,
故选D.
11.解:设需35千克袋,24千克袋,则目标函数元,约束条件为
,当时,,即,这时
三、解答题:
16.某厂生产A与B两种产品,每公斤的产值分别为600元与400元.又知每生产1公斤A产品需要电力2千瓦、煤4吨;而生产1公斤B产品需要电力3千瓦、煤2吨.但该厂的电力供应不得超过100千瓦,煤最多只有120吨.问如何安排生产计划以取得最大产值
解:设生产A与B两种产品分别为x公斤,y公斤,总产值为Z元。则
且
作可行域:
作直线l:600x+400y=0,即直线l:3x+2y=0,把直线l向右上方平移至l1的位置时,直线经过可行域上的点A,且与原点距离最大,此时z=600x+400y取最大值.解方程组
,得A的坐标为x=20,y=20
答:生产A产品20公斤、B产品20公斤才能才能使产值最大。
17.某运输队公司接受了向抗洪抢险地区每天至少运送180t支援物资的任务,该公司有8辆载重量为6t的A型卡车与4辆载重量为10t的B型卡车,有10名驾驶员。每辆卡车每天往返的次数为A型卡车4次,B型卡车3次。每辆卡车每天往返的成本费为A型车320元,B型车504元,请你给该公司调配车辆,使公司所花的成本最低
17.解:设每天调出A型车x辆,B型车y辆,公司所花的成本为z元,则有
且,由图解法可得最优整点解为(5,2),即每天调出A型车5辆,B型车2辆时,公司所花的成本最低。
18.某公司准备进行两种组合投资,稳健型组合投资是由每份金融投资20万元,房地产投资30万元组成;进取型组合投资是由每份金融投资40万元,房地产投资30万元组成。已知每份稳健型组合投资每年可获利10万元,每份进取型组合投资每年可获利15万元。若可作投资用的资金中,金融投资不超过160万元,房地产投资不超过180万元,那么这两种组合投资应注入多少份,才能使一年获利总额最多?
18.解:设稳健型投资份,进取型投资份,利润总额为(×10万元),
则目标函数为(×10万元),
线性约束条件为:,即
作出可行域(图略),解方程组,得交点
作直线,平移,当过点M时,取最大值:万元=70万元。
