安徽省定远县育才学校2020-2021学年高二下学期数学(理)周测试题(3月8日) Word版含解析
文档属性
| 名称 | 安徽省定远县育才学校2020-2021学年高二下学期数学(理)周测试题(3月8日) Word版含解析 |  | |
| 格式 | docx | ||
| 文件大小 | 130.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 20:42:05 | ||
图片预览


文档简介
育才学校2020-2021学年度第二学期周练
高二数学理科
一、选择题(共14小题,每小题5分,共70分)
1.垂直于同一条直线的两条直线一定( )
A. 平行 B. 相交 C. 异面 D. 以上都有可能
2.在空间四边形ABCD的边AB,BC,CD,DA上分别取E,F,G,H四点,如果EF,HG交于一点P,则( )
A.点P一定在直线BD上 B.点P一定在直线AC上
C.点P一定在直线AC或BD上 D.点P既不在直线AC上,也不在直线BD上
39579551377953.如图所示,在正方体ABCD-A1B1C1D1中,O为DB的中点,直线A1C交平面C1BD于点M,则下列结论错误的是( )
A.C1,M,O三点共线 B.C1,M,O,C四点共面
C.C1,O,A,M四点共面D.D1,D,O,M四点共面
4.在正方体ABCD-A1B1C1D1中,E,F分别是侧面AA1D1D,侧面CC1D1D的中心,G,H分别是线段AB,BC的中点,则直线EF与直线GH的位置关系是( )A. 相交 B. 异面 C. 平行 D. 垂直
5.已知在空间四边形ABCD中,M,N分别是AB,CD的中点,且AC=4,BD=6,则( )
A. 1<MN<5 B. 2<MN<10 C. 1≤MN≤5 D. 2<MN<5
36207705930906.两个三角形不在同一平面内,它们的边两两对应平行,那么这两个三角形( )A. 全等 B. 不相似 C. 仅有一个角相等 D. 相似
7.一平面α上,且AB∥CD,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为m,n,那么m+n等于( )A. 8 B. 9 C. 10 D. 11
8.如果直线a与平面α,β所成的角相等,那么平面α与β的位置关系是( )
A.α∥β B.α不一定平行于β C.α不平行于β D. 以上结论都不正确
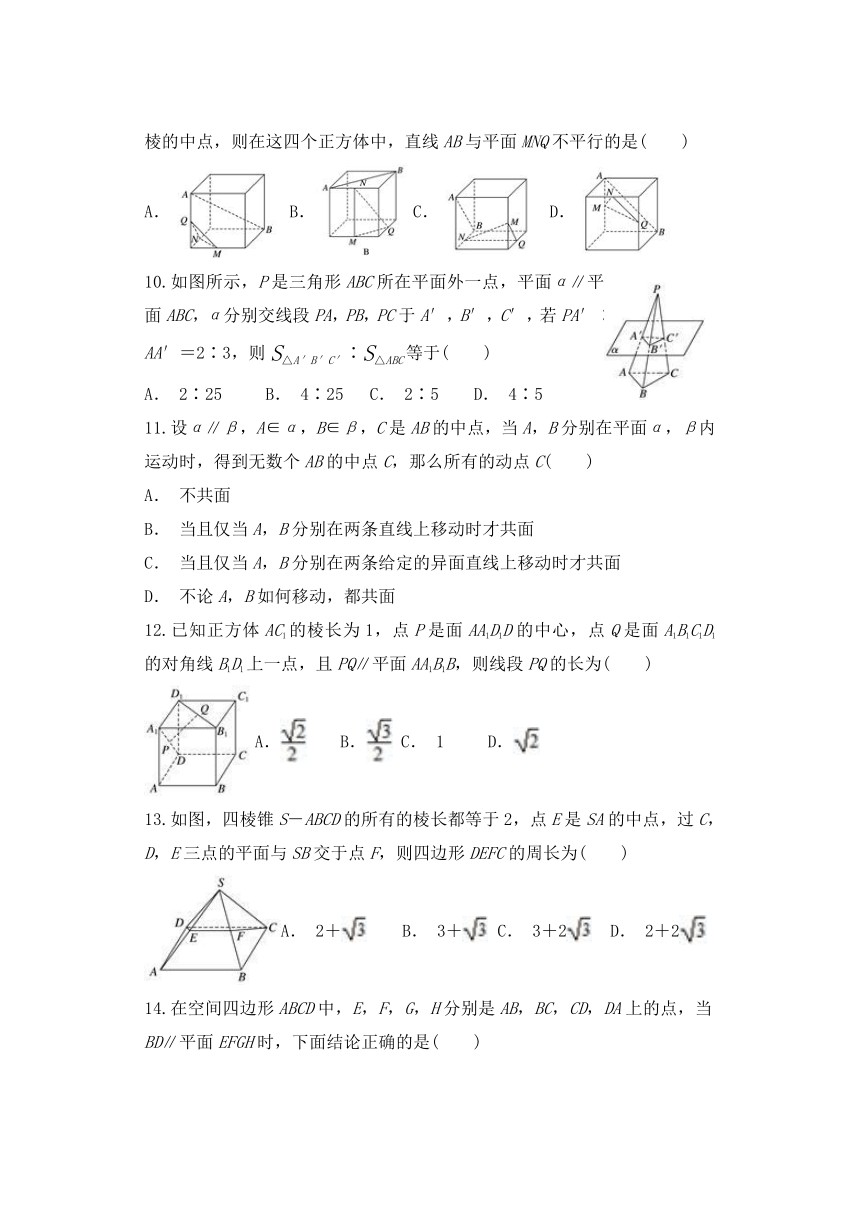
9.如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是( )
A.B.C.D.
404495010414010.如图所示,P是三角形ABC所在平面外一点,平面α∥平面ABC,α分别交线段PA,PB,PC于A′,B′,C′,若PA′∶AA′=2∶3,则S△A′B′C′∶S△ABC等于( )
A. 2∶25 B. 4∶25 C. 2∶5 D. 4∶5
11.设α∥β,A∈α,B∈β,C是AB的中点,当A,B分别在平面α,β内运动时,得到无数个AB的中点C,那么所有的动点C( )
A. 不共面
B. 当且仅当A,B分别在两条直线上移动时才共面
C. 当且仅当A,B分别在两条给定的异面直线上移动时才共面
D. 不论A,B如何移动,都共面
12.已知正方体AC1的棱长为1,点P是面AA1D1D的中心,点Q是面A1B1C1D1的对角线B1D1上一点,且PQ∥平面AA1B1B,则线段PQ的长为( )
A. B. C. 1 D.
13.如图,四棱锥S-ABCD的所有的棱长都等于2,点E是SA的中点,过C,D,E三点的平面与SB交于点F,则四边形DEFC的周长为( )
A. 2+ B. 3+ C. 3+2 D. 2+2
14.在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,当BD∥平面EFGH时,下面结论正确的是( )
A.E,F,G,H一定是各边的中点
B.G,H一定是CD,DA的中点
C.BE∶EA=BF∶FC,且DH∶HA=DG∶GC
D.AE∶EB=AH∶HD,且BF∶FC=DG∶GC
二、填空题(共2小题,每小题5分,共10分)
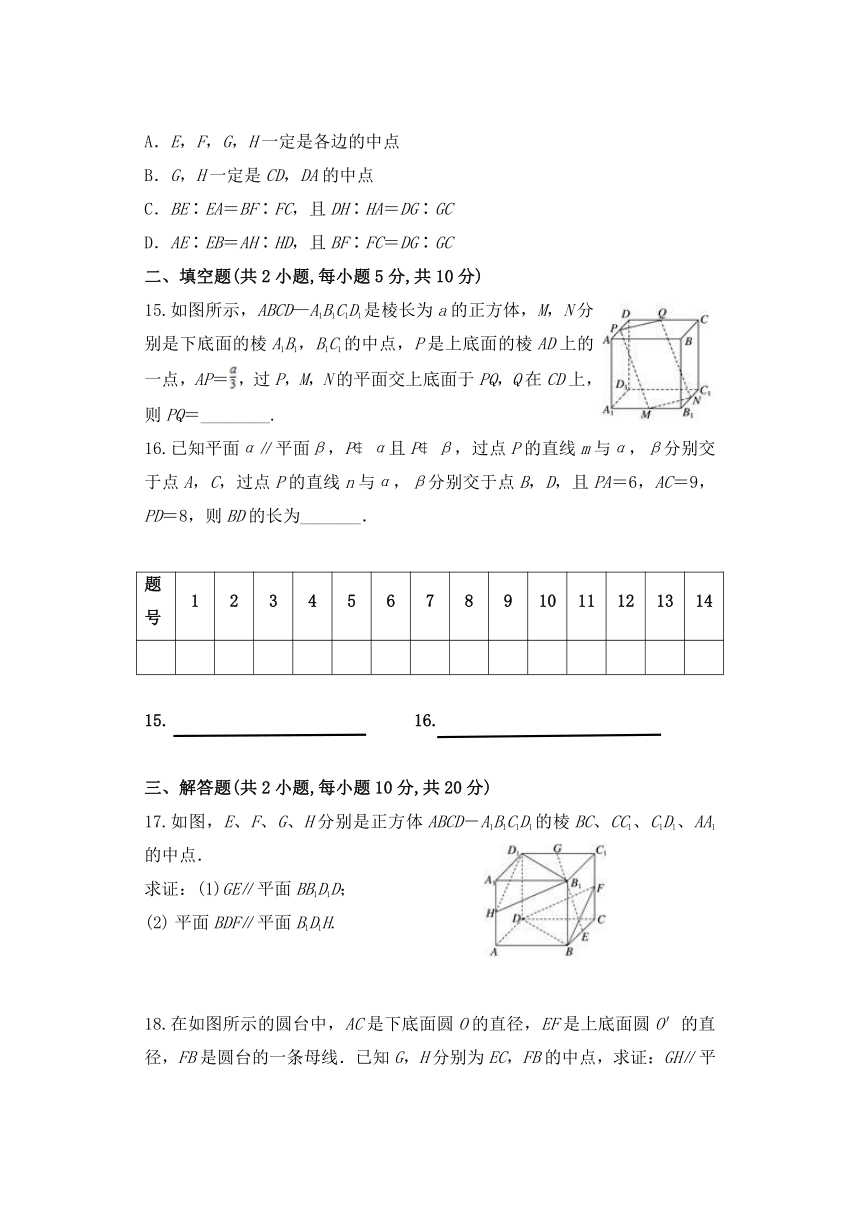
39541453429015.如图所示,ABCD—A1B1C1D1是棱长为a的正方体,M,N分别是下底面的棱A1B1,B1C1的中点,P是上底面的棱AD上的一点,AP=,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ=________.
16.已知平面α∥平面β,P?α且P?β,过点P的直线m与α,β分别交于点A,C,过点P的直线n与α,β分别交于点B,D,且PA=6,AC=9,PD=8,则BD的长为_______.
题号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
2574925228600257175228600 16.
三、解答题(共2小题,每小题10分,共20分)
298450029591017.如图,E、F、G、H分别是正方体ABCD-A1B1C1D1的棱BC、CC1、C1D1、AA1的中点.
求证:(1)GE∥平面BB1D1D;
平面BDF∥平面B1D1H.
18.在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′的直径,FB是圆台的一条母线.已知G,H分别为EC,FB的中点,求证:GH∥平面ABC.
答案解析
1.D
【解析】两条直线同时垂直于同一条直线,这两条直线可能平行、相交、异面.
2.B
【解析】如图,
∵P∈HG,HG?平面ACD,
∴P∈平面ACD.
同理,P∈平面BAC.
∵平面BAC∩平面ACD=AC,∴P∈AC.故选B.
3.D
【解析】在题图中,连接A1C1,AC,
则AC∩BD=O,A1C∩平面C1BD=M.
∴C1,M,O三点在平面C1BD与平面ACC1A1的交线上,
即C1,M,O三点共线,
∴选项A,B,C均正确,D不正确.
4.C
【解析】如图,连接AD1,CD1,AC,则E,F分别为AD1,CD1的中点.由三角形的中位线定理,知EF∥AC,GH∥AC,所以EF∥GH,故选C.
5.A
【解析】取AD的中点H,连接MH,NH,则MH∥BD,且MH=BD,NH∥AC,且NH=AC,且M,N,H三点构成三角形,由三角形中三边关系,可得MH-NH6.D
【解析】由等角定理知,这两个三角形的三个角分别对应相等,故选D.
7.A
【解析】取CD的中点H,连接EH,HF.在四面体CDEF中,CD⊥EH,CD⊥FH,所以CD⊥平面EFH,所以AB⊥平面EFH,所以正方体的左、右两个侧面与EF平行,其余4个平面与EF相交,即n=4.又因为CE与AB在同一平面内,所以CE与正方体下底面共面,与上底面平行,与其余四个面相交,即m=4,所以m+n=4+4=8.
8.B
【解析】如图所示,当两平面平行时,能成等角;当两平面相交时,能成等角.
故选B.
9.A
【解析】A中,作如图①所示的辅助线,其中D为BC的中点,则QD∥AB.
∵QD∩平面MNQ=Q,∴QD与平面MNQ相交,
∴直线AB与平面MNQ相交;
B中,作如图②所示的辅助线,则AB∥CD,CD∥MQ,
∴AB∥MQ,又AB?平面MNQ,MQ?平面MNQ,
∴AB∥平面MNQ;
C中,作如图③所示的辅助线,则AB∥CD,CD∥MQ,
∴AB∥MQ,又AB?平面MNQ,MQ?平面MNQ,
∴AB∥平面MNQ;
D中,作如图④所示的辅助线,则AB∥CD,CD∥NQ,
∴AB∥NQ,又AB?平面MNQ,NQ?平面MNQ,
∴AB∥平面MNQ.故选A.
10.B
【解析】∵平面α∥平面ABC,平面PAB与它们的交线分别为A′B′,AB,∴AB∥A′B′,
同理B′C′∥BC,易得△ABC∽△A′B′C′,
S△A′B′C′∶S△ABC=2=2=.
11.D
【解析】如图所示,A′,B′分别是A,B两点在α,β上运动后的两点,
此时AB的中点C变成A′B′的中点C′,连接A′B,取A′B的中点E.连接CE,C′E,AA′,BB′,CC′,则CE∥AA′,又CE?α,AA′?α,∴CE∥α.
又C′E∥BB′,C′E?β,BB′?β,∴C′E∥β.
又∵α∥β,C′E?α,∴C′E∥α.
∵C′E∩CE=E,C′E,CE?平面CC′E,
∴平面CC′E∥平面α,
∴CC′∥平面α.
∴不论A,B如何移动,所有的动点C都在过C点且与α,β平行的平面上.
12.A
【解析】如图,连接AD1,AB1,∵PQ∥平面AA1B1B,
平面AB1D1∩平面AA1B1B=AB1,
PQ?平面AB1D1,∴PQ∥AB1,
∴PQ=AB1==.
13.C
【解析】∵CD∥AB,CD?平面SAB,AB?平面SAB,
∴CD∥平面SAB.
又平面CDEF∩平面SAB=EF,∴CD∥EF,
又CD∥AB,∴AB∥EF.
∵SE=EA,∴EF为△ABS的中位线,
∴EF=AB=1,
又DE=CF=,
∴四边形DEFC的周长为3+2.
14.D
【解析】由于BD∥平面EFGH,所以有BD∥EH,BD∥FG,则AE∶EB=AH∶HD,且BF∶FC=DG∶GC.
15.a
【解析】∵MN∥平面AC,平面PMN∩平面AC=PQ,
∴MN∥PQ,易知DP=DQ=,
故PQ==DP=.
16.或24
【解析】如图①所示,∵AC∩BD=P,
∴经过直线AC与BD可确定平面PCD.
∵α∥β,α∩平面PCD=AB,β∩平面PCD=CD,
∴AB∥CD.
∴=,
即=,
∴BD=.
如图②所示,同理可证AB∥CD,
∴=,
即=,
∴BD=24.
综上所述,BD的长为或24.
17.证明 (1)取B1D1中点O,连接GO,OB,
易证OGB1C1,
BEB1C1,
∴OGBE,四边形BEGO为平行四边形.
∴OB∥GE.
∵OB?平面BDD1B1,
GE?平面BDD1B1,
∴GE∥平面BDD1B1.
(2)由正方体性质得B1D1∥BD,
∵B1D1?平面BDF,BD?平面BDF,
∴B1D1∥平面BDF.
连接HB,D1F,
易证HBFD1是平行四边形,∴HD1∥BF.
∵HD1?平面BDF,BF?平面BDF,
∴HD1∥平面BDF.
∵B1D1∩HD1=D1,
∴平面BDF∥平面B1D1H.
18.证明 设FC的中点为I,连接GI,HI,
在△CEF中,因为G是CE的中点,所以GI∥EF,
又EF∥OB,所以GI∥OB,
在△CFB中,因为H是FB的中点,
所以HI∥BC,又HI∩GI=I,OB∩BC=B,HI,GI?平面GHI,OB,BC?平面ABC,
所以平面GHI∥平面ABC,
因为GH?平面GHI,
所以GH∥平面ABC.
高二数学理科
一、选择题(共14小题,每小题5分,共70分)
1.垂直于同一条直线的两条直线一定( )
A. 平行 B. 相交 C. 异面 D. 以上都有可能
2.在空间四边形ABCD的边AB,BC,CD,DA上分别取E,F,G,H四点,如果EF,HG交于一点P,则( )
A.点P一定在直线BD上 B.点P一定在直线AC上
C.点P一定在直线AC或BD上 D.点P既不在直线AC上,也不在直线BD上
39579551377953.如图所示,在正方体ABCD-A1B1C1D1中,O为DB的中点,直线A1C交平面C1BD于点M,则下列结论错误的是( )
A.C1,M,O三点共线 B.C1,M,O,C四点共面
C.C1,O,A,M四点共面D.D1,D,O,M四点共面
4.在正方体ABCD-A1B1C1D1中,E,F分别是侧面AA1D1D,侧面CC1D1D的中心,G,H分别是线段AB,BC的中点,则直线EF与直线GH的位置关系是( )A. 相交 B. 异面 C. 平行 D. 垂直
5.已知在空间四边形ABCD中,M,N分别是AB,CD的中点,且AC=4,BD=6,则( )
A. 1<MN<5 B. 2<MN<10 C. 1≤MN≤5 D. 2<MN<5
36207705930906.两个三角形不在同一平面内,它们的边两两对应平行,那么这两个三角形( )A. 全等 B. 不相似 C. 仅有一个角相等 D. 相似
7.一平面α上,且AB∥CD,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为m,n,那么m+n等于( )A. 8 B. 9 C. 10 D. 11
8.如果直线a与平面α,β所成的角相等,那么平面α与β的位置关系是( )
A.α∥β B.α不一定平行于β C.α不平行于β D. 以上结论都不正确
9.如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是( )
A.B.C.D.
404495010414010.如图所示,P是三角形ABC所在平面外一点,平面α∥平面ABC,α分别交线段PA,PB,PC于A′,B′,C′,若PA′∶AA′=2∶3,则S△A′B′C′∶S△ABC等于( )
A. 2∶25 B. 4∶25 C. 2∶5 D. 4∶5
11.设α∥β,A∈α,B∈β,C是AB的中点,当A,B分别在平面α,β内运动时,得到无数个AB的中点C,那么所有的动点C( )
A. 不共面
B. 当且仅当A,B分别在两条直线上移动时才共面
C. 当且仅当A,B分别在两条给定的异面直线上移动时才共面
D. 不论A,B如何移动,都共面
12.已知正方体AC1的棱长为1,点P是面AA1D1D的中心,点Q是面A1B1C1D1的对角线B1D1上一点,且PQ∥平面AA1B1B,则线段PQ的长为( )
A. B. C. 1 D.
13.如图,四棱锥S-ABCD的所有的棱长都等于2,点E是SA的中点,过C,D,E三点的平面与SB交于点F,则四边形DEFC的周长为( )
A. 2+ B. 3+ C. 3+2 D. 2+2
14.在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,当BD∥平面EFGH时,下面结论正确的是( )
A.E,F,G,H一定是各边的中点
B.G,H一定是CD,DA的中点
C.BE∶EA=BF∶FC,且DH∶HA=DG∶GC
D.AE∶EB=AH∶HD,且BF∶FC=DG∶GC
二、填空题(共2小题,每小题5分,共10分)
39541453429015.如图所示,ABCD—A1B1C1D1是棱长为a的正方体,M,N分别是下底面的棱A1B1,B1C1的中点,P是上底面的棱AD上的一点,AP=,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ=________.
16.已知平面α∥平面β,P?α且P?β,过点P的直线m与α,β分别交于点A,C,过点P的直线n与α,β分别交于点B,D,且PA=6,AC=9,PD=8,则BD的长为_______.
题号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
2574925228600257175228600 16.
三、解答题(共2小题,每小题10分,共20分)
298450029591017.如图,E、F、G、H分别是正方体ABCD-A1B1C1D1的棱BC、CC1、C1D1、AA1的中点.
求证:(1)GE∥平面BB1D1D;
平面BDF∥平面B1D1H.
18.在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′的直径,FB是圆台的一条母线.已知G,H分别为EC,FB的中点,求证:GH∥平面ABC.
答案解析
1.D
【解析】两条直线同时垂直于同一条直线,这两条直线可能平行、相交、异面.
2.B
【解析】如图,
∵P∈HG,HG?平面ACD,
∴P∈平面ACD.
同理,P∈平面BAC.
∵平面BAC∩平面ACD=AC,∴P∈AC.故选B.
3.D
【解析】在题图中,连接A1C1,AC,
则AC∩BD=O,A1C∩平面C1BD=M.
∴C1,M,O三点在平面C1BD与平面ACC1A1的交线上,
即C1,M,O三点共线,
∴选项A,B,C均正确,D不正确.
4.C
【解析】如图,连接AD1,CD1,AC,则E,F分别为AD1,CD1的中点.由三角形的中位线定理,知EF∥AC,GH∥AC,所以EF∥GH,故选C.
5.A
【解析】取AD的中点H,连接MH,NH,则MH∥BD,且MH=BD,NH∥AC,且NH=AC,且M,N,H三点构成三角形,由三角形中三边关系,可得MH-NH
【解析】由等角定理知,这两个三角形的三个角分别对应相等,故选D.
7.A
【解析】取CD的中点H,连接EH,HF.在四面体CDEF中,CD⊥EH,CD⊥FH,所以CD⊥平面EFH,所以AB⊥平面EFH,所以正方体的左、右两个侧面与EF平行,其余4个平面与EF相交,即n=4.又因为CE与AB在同一平面内,所以CE与正方体下底面共面,与上底面平行,与其余四个面相交,即m=4,所以m+n=4+4=8.
8.B
【解析】如图所示,当两平面平行时,能成等角;当两平面相交时,能成等角.
故选B.
9.A
【解析】A中,作如图①所示的辅助线,其中D为BC的中点,则QD∥AB.
∵QD∩平面MNQ=Q,∴QD与平面MNQ相交,
∴直线AB与平面MNQ相交;
B中,作如图②所示的辅助线,则AB∥CD,CD∥MQ,
∴AB∥MQ,又AB?平面MNQ,MQ?平面MNQ,
∴AB∥平面MNQ;
C中,作如图③所示的辅助线,则AB∥CD,CD∥MQ,
∴AB∥MQ,又AB?平面MNQ,MQ?平面MNQ,
∴AB∥平面MNQ;
D中,作如图④所示的辅助线,则AB∥CD,CD∥NQ,
∴AB∥NQ,又AB?平面MNQ,NQ?平面MNQ,
∴AB∥平面MNQ.故选A.
10.B
【解析】∵平面α∥平面ABC,平面PAB与它们的交线分别为A′B′,AB,∴AB∥A′B′,
同理B′C′∥BC,易得△ABC∽△A′B′C′,
S△A′B′C′∶S△ABC=2=2=.
11.D
【解析】如图所示,A′,B′分别是A,B两点在α,β上运动后的两点,
此时AB的中点C变成A′B′的中点C′,连接A′B,取A′B的中点E.连接CE,C′E,AA′,BB′,CC′,则CE∥AA′,又CE?α,AA′?α,∴CE∥α.
又C′E∥BB′,C′E?β,BB′?β,∴C′E∥β.
又∵α∥β,C′E?α,∴C′E∥α.
∵C′E∩CE=E,C′E,CE?平面CC′E,
∴平面CC′E∥平面α,
∴CC′∥平面α.
∴不论A,B如何移动,所有的动点C都在过C点且与α,β平行的平面上.
12.A
【解析】如图,连接AD1,AB1,∵PQ∥平面AA1B1B,
平面AB1D1∩平面AA1B1B=AB1,
PQ?平面AB1D1,∴PQ∥AB1,
∴PQ=AB1==.
13.C
【解析】∵CD∥AB,CD?平面SAB,AB?平面SAB,
∴CD∥平面SAB.
又平面CDEF∩平面SAB=EF,∴CD∥EF,
又CD∥AB,∴AB∥EF.
∵SE=EA,∴EF为△ABS的中位线,
∴EF=AB=1,
又DE=CF=,
∴四边形DEFC的周长为3+2.
14.D
【解析】由于BD∥平面EFGH,所以有BD∥EH,BD∥FG,则AE∶EB=AH∶HD,且BF∶FC=DG∶GC.
15.a
【解析】∵MN∥平面AC,平面PMN∩平面AC=PQ,
∴MN∥PQ,易知DP=DQ=,
故PQ==DP=.
16.或24
【解析】如图①所示,∵AC∩BD=P,
∴经过直线AC与BD可确定平面PCD.
∵α∥β,α∩平面PCD=AB,β∩平面PCD=CD,
∴AB∥CD.
∴=,
即=,
∴BD=.
如图②所示,同理可证AB∥CD,
∴=,
即=,
∴BD=24.
综上所述,BD的长为或24.
17.证明 (1)取B1D1中点O,连接GO,OB,
易证OGB1C1,
BEB1C1,
∴OGBE,四边形BEGO为平行四边形.
∴OB∥GE.
∵OB?平面BDD1B1,
GE?平面BDD1B1,
∴GE∥平面BDD1B1.
(2)由正方体性质得B1D1∥BD,
∵B1D1?平面BDF,BD?平面BDF,
∴B1D1∥平面BDF.
连接HB,D1F,
易证HBFD1是平行四边形,∴HD1∥BF.
∵HD1?平面BDF,BF?平面BDF,
∴HD1∥平面BDF.
∵B1D1∩HD1=D1,
∴平面BDF∥平面B1D1H.
18.证明 设FC的中点为I,连接GI,HI,
在△CEF中,因为G是CE的中点,所以GI∥EF,
又EF∥OB,所以GI∥OB,
在△CFB中,因为H是FB的中点,
所以HI∥BC,又HI∩GI=I,OB∩BC=B,HI,GI?平面GHI,OB,BC?平面ABC,
所以平面GHI∥平面ABC,
因为GH?平面GHI,
所以GH∥平面ABC.
同课章节目录
