_第三章直线与方程检测试题 2020-2021学年高一数学人教A版必修2第三章(Word含解析)
文档属性
| 名称 | _第三章直线与方程检测试题 2020-2021学年高一数学人教A版必修2第三章(Word含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 138.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 00:00:00 | ||
图片预览



文档简介
第三章检测试题
时间:90分钟 分值:120分
第Ⅰ卷(选择题,共60分)
一、选择题(每小题5分,共60分)
1.直线l经过原点和(1,-1),则l的倾斜角是( )
A.45° B.-45°
C.135° D.45°或135°
2.已知点A(0,4),B(4,0)在直线l上,则l的方程为( )
A.x+y-4=0 B.x-y-4=0
C.x+y+4=0 D.x-y+4=0
3.过点M(-2,a),N(a,4)的直线的斜率为-,则|MN|
=( )
A.10 B.180
C.6 D.6
4.已知直线l与过点M(-,),N(,-)的直线垂直,则直线l的倾斜角是( )
A. B.
C. D.
5.若直线mx+ny+3=0在y轴上的截距为-3,且它的倾斜角是直线x-y=3的倾斜角的2倍,则( )
A.m=-,n=1 B.m=-,n=-3
C.m=,n=-3 D.m=,n=1
6.到直线3x-4y-1=0的距离为2的直线方程是( )
A.3x-4y-11=0
B.3x-4y-11=0或3x-4y+9=0
C.3x-4y+9=0
D.3x-4y+11=0或3x-4y-9=0
7.已知A(2,4)与B(3,3)关于直线l对称,则直线l的方程为( )
A.x+y=0 B.x-y=0
C.x+y-6=0 D.x-y+1=0
8.已知直线mx+ny+1=0平行于直线4x+3y+5=0,且在y轴上的截距为,则m,n的值分别为( )
A.4和3 B.-4和3
C.-4和-3 D.4和-3
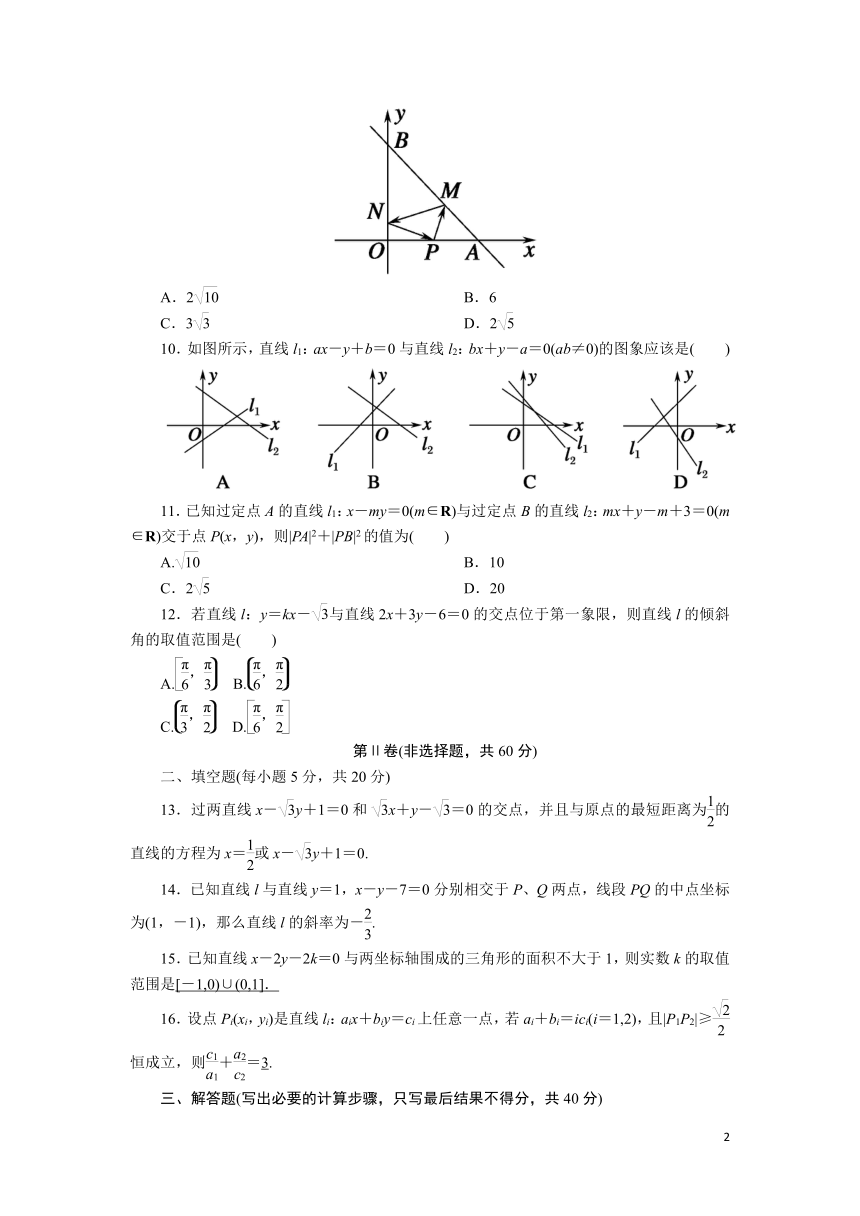
9.如图,已知A(4,0)、B(0,4),从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是( )
A.2 B.6
C.3 D.2
10.如图所示,直线l1:ax-y+b=0与直线l2:bx+y-a=0(ab≠0)的图象应该是( )
11.已知过定点A的直线l1:x-my=0(m∈R)与过定点B的直线l2:mx+y-m+3=0(m∈R)交于点P(x,y),则|PA|2+|PB|2的值为( )
A. B.10
C.2 D.20
12.若直线l:y=kx-与直线2x+3y-6=0的交点位于第一象限,则直线l的倾斜角的取值范围是( )
A. B.
C. D.
第Ⅱ卷(非选择题,共60分)
二、填空题(每小题5分,共20分)
13.过两直线x-y+1=0和x+y-=0的交点,并且与原点的最短距离为的直线的方程为x=或x-y+1=0.
14.已知直线l与直线y=1,x-y-7=0分别相交于P、Q两点,线段PQ的中点坐标为(1,-1),那么直线l的斜率为-.
15.已知直线x-2y-2k=0与两坐标轴围成的三角形的面积不大于1,则实数k的取值范围是[-1,0)∪(0,1].
16.设点Pi(xi,yi)是直线li:aix+biy=ci上任意一点,若ai+bi=ici(i=1,2),且|P1P2|≥恒成立,则+=3.
三、解答题(写出必要的计算步骤,只写最后结果不得分,共40分)
17.(10分)已知直线l经过点(0,-2),其倾斜角的大小是60°.
(1)求直线l的方程;
(2)求直线l与两坐标轴围成的三角形的面积.
18.(10分)已知两直线l1:mx+8y+n=0和l2:2x+my-1=0.
(1)若l1与l2交于点P(m,-1),求m,n的值;
(2)若l1∥l2,试确定m,n需要满足的条件;
(3)若l1⊥l2,试确定m,n需要满足的条件.
19.(10分)已知直线l1:y=-k(x-a)和直线l2在x轴上的截距相等,且它们的倾斜角互补,且直线l1过点P(-3,3).如果点Q(2,2)到直线l2的距离为1,求l2的方程.
20.(10分)在△ABC中,BC边上的高所在直线的方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0.若点B的坐标为(1,2),求点A和点C的坐标.
第三章检测试题
时间:90分钟 分值:120分
第Ⅰ卷(选择题,共60分)
一、选择题(每小题5分,共60分)
1.直线l经过原点和(1,-1),则l的倾斜角是( C )
A.45° B.-45°
C.135° D.45°或135°
解析:∵直线l经过坐标原点和点(1,-1),∴直线l的斜率k==-1,∴直线l的倾斜角α=135°,故选C.
2.已知点A(0,4),B(4,0)在直线l上,则l的方程为( A )
A.x+y-4=0 B.x-y-4=0
C.x+y+4=0 D.x-y+4=0
解析:由截距式方程可得l的方程为+=1,即x+y-4=0.
3.过点M(-2,a),N(a,4)的直线的斜率为-,则|MN|
=( D )
A.10 B.180
C.6 D.6
解析:∵过点M(-2,a),N(a,4)的直线的斜率k==-,解得a=10,
∴|MN|=
==6.故选D.
4.已知直线l与过点M(-,),N(,-)的直线垂直,则直线l的倾斜角是( B )
A. B.
C. D.
解析:因为kMN==-1,所以kl=1,由此可得,直线l的倾斜角为.
5.若直线mx+ny+3=0在y轴上的截距为-3,且它的倾斜角是直线x-y=3的倾斜角的2倍,则( D )
A.m=-,n=1 B.m=-,n=-3
C.m=,n=-3 D.m=,n=1
解析:依题意得-=-3,-=tan120°=-,得m=,n=1.故选D.
6.到直线3x-4y-1=0的距离为2的直线方程是( B )
A.3x-4y-11=0
B.3x-4y-11=0或3x-4y+9=0
C.3x-4y+9=0
D.3x-4y+11=0或3x-4y-9=0
解析:本题可采用排除法,显然不能选择A,C.又因为直线3x-4y+11=0到直线3x-4y-1=0的距离为,故不能选择D,所以答案为B.
7.已知A(2,4)与B(3,3)关于直线l对称,则直线l的方程为( D )
A.x+y=0 B.x-y=0
C.x+y-6=0 D.x-y+1=0
解析:由已知得直线l是线段AB的垂直平分线,所以直线l的斜率为1,且过线段中点,由点斜式得方程为y-=x-,整理得x-y+1=0.故选D.
8.已知直线mx+ny+1=0平行于直线4x+3y+5=0,且在y轴上的截距为,则m,n的值分别为( C )
A.4和3 B.-4和3
C.-4和-3 D.4和-3
解析:由题意知:-=-,即3m=4n,且有-=,∴n=-3,m=-4.
9.如图,已知A(4,0)、B(0,4),从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是( A )
A.2 B.6
C.3 D.2
解析:
如图,由题意知点P关于直线AB的对称点为D(4,2),关于y轴的对称点为C(-2,0),则光线所经过的路程PMN的长为|CD|=2.
10.如图所示,直线l1:ax-y+b=0与直线l2:bx+y-a=0(ab≠0)的图象应该是( B )
解析:∵ab≠0,∴可把l1和l2的方程都化成斜截式,得l1:y=ax+b,l2:y=-bx+a,∴l1的斜率等于l2在y轴上的截距.∵C中l1的斜率小于0,l2在y轴上的截距大于0;D中l1的斜率大于0,l2在y轴上的截距小于0,∴可排除C,D两选项.又∵l1在y轴上的截距等于l2的斜率的相反数,∴可排除A.故选B.
11.已知过定点A的直线l1:x-my=0(m∈R)与过定点B的直线l2:mx+y-m+3=0(m∈R)交于点P(x,y),则|PA|2+|PB|2的值为( B )
A. B.10
C.2 D.20
解析:易知直线l1:x-my=0过定点A(0,0).直线l2:mx+y-m+3=0化为m(x-1)+y+3=0,
令解得
∴l2过定点B(1,-3).∵直线l1与l2垂直,∴|PA|2+|PB|2=|AB|2=10.故选B.
12.若直线l:y=kx-与直线2x+3y-6=0的交点位于第一象限,则直线l的倾斜角的取值范围是( B )
A. B.
C. D.
解析:
如图所示,直线2x+3y-6=0过点A(3,0),B(0,2),直线l必过点C(0,-),当直线l过A点时,两直线的交点在x轴,当直线l绕C点逆时针旋转时,交点进入第一象限,从而可得直线l的倾斜角的取值范围是.
第Ⅱ卷(非选择题,共60分)
二、填空题(每小题5分,共20分)
13.过两直线x-y+1=0和x+y-=0的交点,并且与原点的最短距离为的直线的方程为x=或x-y+1=0.
解析:易求得两直线交点的坐标为,,显然直线x=满足条件.当斜率存在时,设过该点的直线方程为y-=kx-,化为一般式得2kx-2y+-k=0,因为直线与原点的最短距离为,所以=,解得k=,所以所求直线的方程为x-y+1=0.
14.已知直线l与直线y=1,x-y-7=0分别相交于P、Q两点,线段PQ的中点坐标为(1,-1),那么直线l的斜率为-.
解析:设P(x,1),则Q(2-x,-3),将Q坐标代入x-y-7=0得,2-x+3-7=0.∴x=-2,∴P(-2,1),∴kl=-.
15.已知直线x-2y-2k=0与两坐标轴围成的三角形的面积不大于1,则实数k的取值范围是[-1,0)∪(0,1].
解析:令x=0,得y=-k,令y=0,得x=2k,∴三角形的面积S=|xy|=k2.又S≤1,即k2≤1,∴-1≤k≤1.又当k=0时,直线过原点,与两坐标轴构不成三角形,故应舍去,∴实数k的取值范围是[-1,0)∪(0,1].
16.设点Pi(xi,yi)是直线li:aix+biy=ci上任意一点,若ai+bi=ici(i=1,2),且|P1P2|≥恒成立,则+=3.
解析:∵点Pi(xi,yi)在直线li:aix+biy=ci上,ai+bi=ici(i=1,2),∴l1过定点M(1,1),l2过定点N,∴|MN|==,又|P1P2|≥恒成立,∴l1∥l2,MN⊥li(i=1,2).又kMN=1,∴直线l1,l2的方程分别为x+y=2,x+y=1,∴+=2+1=3.
三、解答题(写出必要的计算步骤,只写最后结果不得分,共40分)
17.(10分)已知直线l经过点(0,-2),其倾斜角的大小是60°.
(1)求直线l的方程;
(2)求直线l与两坐标轴围成的三角形的面积.
解:(1)由直线的点斜式方程得直线l的方程为y+2=tan60°x,即x-y-2=0.
(2)设直线l与x轴、y轴的交点分别为A,B,令y=0得x=;令x=0得y=-2.
所以S△OAB=|OA|·|OB|=××2=,故所求三角形的面积为.
18.(10分)已知两直线l1:mx+8y+n=0和l2:2x+my-1=0.
(1)若l1与l2交于点P(m,-1),求m,n的值;
(2)若l1∥l2,试确定m,n需要满足的条件;
(3)若l1⊥l2,试确定m,n需要满足的条件.
解:(1)将点P(m,-1)代入两直线方程得:m2-8+n=0和2m-m-1=0,解得m=1,n=7.
(2)由l1∥l2得:m2-8×2=0?m=±4,又两直线不能重合,所以有8×(-1)-nm≠0,对应得n≠±2,所以当m=4,n≠-2或m=-4,n≠2时,l1∥l2.
(3)当m=0时,直线l1:y=-和l2:x=,此时l1⊥l2,
当m≠0时,此时两直线的斜率之积等于,显然l1与l2不垂直,
所以当m=0,n∈R时直线l1和l2垂直.
19.(10分)已知直线l1:y=-k(x-a)和直线l2在x轴上的截距相等,且它们的倾斜角互补,且直线l1过点P(-3,3).如果点Q(2,2)到直线l2的距离为1,求l2的方程.
解:由题意,可设直线l2的方程为y=k(x-a),即kx-y-ak=0,
∵点Q(2,2)到直线l2的距离为1,
∴=1.①
又∵直线l1的方程为y=-k(x-a),且直线l1过点P(-3,3),∴ak=3-3k.②
由①②得=1,两边平方整理得12k2-25k+12=0,解得k=或k=,
∴当k=时,代入②得a=-,此时直线l2的方程为4x-3y+3=0;
当k=时,代入②得a=1,此时直线l2的方程为3x-4y-3=0.
综上所述,直线l2的方程为4x-3y+3=0或3x-4y-3=0.
20.(10分)在△ABC中,BC边上的高所在直线的方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0.若点B的坐标为(1,2),求点A和点C的坐标.
解:由方程组
解得点A的坐标为(-1,0).
又直线AB的斜率kAB=1,x轴是∠A的平分线,所以kAC=-1,则AC边所在的直线方程为y=-(x+1).①
又已知BC边上的高所在直线的方程为x-2y+1=0,故直线BC的斜率kBC=-2,
所以BC边所在的直线方程为y-2=-2(x-1).②
解①②组成的方程组得
即顶点C的坐标为(5,-6).
6
时间:90分钟 分值:120分
第Ⅰ卷(选择题,共60分)
一、选择题(每小题5分,共60分)
1.直线l经过原点和(1,-1),则l的倾斜角是( )
A.45° B.-45°
C.135° D.45°或135°
2.已知点A(0,4),B(4,0)在直线l上,则l的方程为( )
A.x+y-4=0 B.x-y-4=0
C.x+y+4=0 D.x-y+4=0
3.过点M(-2,a),N(a,4)的直线的斜率为-,则|MN|
=( )
A.10 B.180
C.6 D.6
4.已知直线l与过点M(-,),N(,-)的直线垂直,则直线l的倾斜角是( )
A. B.
C. D.
5.若直线mx+ny+3=0在y轴上的截距为-3,且它的倾斜角是直线x-y=3的倾斜角的2倍,则( )
A.m=-,n=1 B.m=-,n=-3
C.m=,n=-3 D.m=,n=1
6.到直线3x-4y-1=0的距离为2的直线方程是( )
A.3x-4y-11=0
B.3x-4y-11=0或3x-4y+9=0
C.3x-4y+9=0
D.3x-4y+11=0或3x-4y-9=0
7.已知A(2,4)与B(3,3)关于直线l对称,则直线l的方程为( )
A.x+y=0 B.x-y=0
C.x+y-6=0 D.x-y+1=0
8.已知直线mx+ny+1=0平行于直线4x+3y+5=0,且在y轴上的截距为,则m,n的值分别为( )
A.4和3 B.-4和3
C.-4和-3 D.4和-3
9.如图,已知A(4,0)、B(0,4),从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是( )
A.2 B.6
C.3 D.2
10.如图所示,直线l1:ax-y+b=0与直线l2:bx+y-a=0(ab≠0)的图象应该是( )
11.已知过定点A的直线l1:x-my=0(m∈R)与过定点B的直线l2:mx+y-m+3=0(m∈R)交于点P(x,y),则|PA|2+|PB|2的值为( )
A. B.10
C.2 D.20
12.若直线l:y=kx-与直线2x+3y-6=0的交点位于第一象限,则直线l的倾斜角的取值范围是( )
A. B.
C. D.
第Ⅱ卷(非选择题,共60分)
二、填空题(每小题5分,共20分)
13.过两直线x-y+1=0和x+y-=0的交点,并且与原点的最短距离为的直线的方程为x=或x-y+1=0.
14.已知直线l与直线y=1,x-y-7=0分别相交于P、Q两点,线段PQ的中点坐标为(1,-1),那么直线l的斜率为-.
15.已知直线x-2y-2k=0与两坐标轴围成的三角形的面积不大于1,则实数k的取值范围是[-1,0)∪(0,1].
16.设点Pi(xi,yi)是直线li:aix+biy=ci上任意一点,若ai+bi=ici(i=1,2),且|P1P2|≥恒成立,则+=3.
三、解答题(写出必要的计算步骤,只写最后结果不得分,共40分)
17.(10分)已知直线l经过点(0,-2),其倾斜角的大小是60°.
(1)求直线l的方程;
(2)求直线l与两坐标轴围成的三角形的面积.
18.(10分)已知两直线l1:mx+8y+n=0和l2:2x+my-1=0.
(1)若l1与l2交于点P(m,-1),求m,n的值;
(2)若l1∥l2,试确定m,n需要满足的条件;
(3)若l1⊥l2,试确定m,n需要满足的条件.
19.(10分)已知直线l1:y=-k(x-a)和直线l2在x轴上的截距相等,且它们的倾斜角互补,且直线l1过点P(-3,3).如果点Q(2,2)到直线l2的距离为1,求l2的方程.
20.(10分)在△ABC中,BC边上的高所在直线的方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0.若点B的坐标为(1,2),求点A和点C的坐标.
第三章检测试题
时间:90分钟 分值:120分
第Ⅰ卷(选择题,共60分)
一、选择题(每小题5分,共60分)
1.直线l经过原点和(1,-1),则l的倾斜角是( C )
A.45° B.-45°
C.135° D.45°或135°
解析:∵直线l经过坐标原点和点(1,-1),∴直线l的斜率k==-1,∴直线l的倾斜角α=135°,故选C.
2.已知点A(0,4),B(4,0)在直线l上,则l的方程为( A )
A.x+y-4=0 B.x-y-4=0
C.x+y+4=0 D.x-y+4=0
解析:由截距式方程可得l的方程为+=1,即x+y-4=0.
3.过点M(-2,a),N(a,4)的直线的斜率为-,则|MN|
=( D )
A.10 B.180
C.6 D.6
解析:∵过点M(-2,a),N(a,4)的直线的斜率k==-,解得a=10,
∴|MN|=
==6.故选D.
4.已知直线l与过点M(-,),N(,-)的直线垂直,则直线l的倾斜角是( B )
A. B.
C. D.
解析:因为kMN==-1,所以kl=1,由此可得,直线l的倾斜角为.
5.若直线mx+ny+3=0在y轴上的截距为-3,且它的倾斜角是直线x-y=3的倾斜角的2倍,则( D )
A.m=-,n=1 B.m=-,n=-3
C.m=,n=-3 D.m=,n=1
解析:依题意得-=-3,-=tan120°=-,得m=,n=1.故选D.
6.到直线3x-4y-1=0的距离为2的直线方程是( B )
A.3x-4y-11=0
B.3x-4y-11=0或3x-4y+9=0
C.3x-4y+9=0
D.3x-4y+11=0或3x-4y-9=0
解析:本题可采用排除法,显然不能选择A,C.又因为直线3x-4y+11=0到直线3x-4y-1=0的距离为,故不能选择D,所以答案为B.
7.已知A(2,4)与B(3,3)关于直线l对称,则直线l的方程为( D )
A.x+y=0 B.x-y=0
C.x+y-6=0 D.x-y+1=0
解析:由已知得直线l是线段AB的垂直平分线,所以直线l的斜率为1,且过线段中点,由点斜式得方程为y-=x-,整理得x-y+1=0.故选D.
8.已知直线mx+ny+1=0平行于直线4x+3y+5=0,且在y轴上的截距为,则m,n的值分别为( C )
A.4和3 B.-4和3
C.-4和-3 D.4和-3
解析:由题意知:-=-,即3m=4n,且有-=,∴n=-3,m=-4.
9.如图,已知A(4,0)、B(0,4),从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是( A )
A.2 B.6
C.3 D.2
解析:
如图,由题意知点P关于直线AB的对称点为D(4,2),关于y轴的对称点为C(-2,0),则光线所经过的路程PMN的长为|CD|=2.
10.如图所示,直线l1:ax-y+b=0与直线l2:bx+y-a=0(ab≠0)的图象应该是( B )
解析:∵ab≠0,∴可把l1和l2的方程都化成斜截式,得l1:y=ax+b,l2:y=-bx+a,∴l1的斜率等于l2在y轴上的截距.∵C中l1的斜率小于0,l2在y轴上的截距大于0;D中l1的斜率大于0,l2在y轴上的截距小于0,∴可排除C,D两选项.又∵l1在y轴上的截距等于l2的斜率的相反数,∴可排除A.故选B.
11.已知过定点A的直线l1:x-my=0(m∈R)与过定点B的直线l2:mx+y-m+3=0(m∈R)交于点P(x,y),则|PA|2+|PB|2的值为( B )
A. B.10
C.2 D.20
解析:易知直线l1:x-my=0过定点A(0,0).直线l2:mx+y-m+3=0化为m(x-1)+y+3=0,
令解得
∴l2过定点B(1,-3).∵直线l1与l2垂直,∴|PA|2+|PB|2=|AB|2=10.故选B.
12.若直线l:y=kx-与直线2x+3y-6=0的交点位于第一象限,则直线l的倾斜角的取值范围是( B )
A. B.
C. D.
解析:
如图所示,直线2x+3y-6=0过点A(3,0),B(0,2),直线l必过点C(0,-),当直线l过A点时,两直线的交点在x轴,当直线l绕C点逆时针旋转时,交点进入第一象限,从而可得直线l的倾斜角的取值范围是.
第Ⅱ卷(非选择题,共60分)
二、填空题(每小题5分,共20分)
13.过两直线x-y+1=0和x+y-=0的交点,并且与原点的最短距离为的直线的方程为x=或x-y+1=0.
解析:易求得两直线交点的坐标为,,显然直线x=满足条件.当斜率存在时,设过该点的直线方程为y-=kx-,化为一般式得2kx-2y+-k=0,因为直线与原点的最短距离为,所以=,解得k=,所以所求直线的方程为x-y+1=0.
14.已知直线l与直线y=1,x-y-7=0分别相交于P、Q两点,线段PQ的中点坐标为(1,-1),那么直线l的斜率为-.
解析:设P(x,1),则Q(2-x,-3),将Q坐标代入x-y-7=0得,2-x+3-7=0.∴x=-2,∴P(-2,1),∴kl=-.
15.已知直线x-2y-2k=0与两坐标轴围成的三角形的面积不大于1,则实数k的取值范围是[-1,0)∪(0,1].
解析:令x=0,得y=-k,令y=0,得x=2k,∴三角形的面积S=|xy|=k2.又S≤1,即k2≤1,∴-1≤k≤1.又当k=0时,直线过原点,与两坐标轴构不成三角形,故应舍去,∴实数k的取值范围是[-1,0)∪(0,1].
16.设点Pi(xi,yi)是直线li:aix+biy=ci上任意一点,若ai+bi=ici(i=1,2),且|P1P2|≥恒成立,则+=3.
解析:∵点Pi(xi,yi)在直线li:aix+biy=ci上,ai+bi=ici(i=1,2),∴l1过定点M(1,1),l2过定点N,∴|MN|==,又|P1P2|≥恒成立,∴l1∥l2,MN⊥li(i=1,2).又kMN=1,∴直线l1,l2的方程分别为x+y=2,x+y=1,∴+=2+1=3.
三、解答题(写出必要的计算步骤,只写最后结果不得分,共40分)
17.(10分)已知直线l经过点(0,-2),其倾斜角的大小是60°.
(1)求直线l的方程;
(2)求直线l与两坐标轴围成的三角形的面积.
解:(1)由直线的点斜式方程得直线l的方程为y+2=tan60°x,即x-y-2=0.
(2)设直线l与x轴、y轴的交点分别为A,B,令y=0得x=;令x=0得y=-2.
所以S△OAB=|OA|·|OB|=××2=,故所求三角形的面积为.
18.(10分)已知两直线l1:mx+8y+n=0和l2:2x+my-1=0.
(1)若l1与l2交于点P(m,-1),求m,n的值;
(2)若l1∥l2,试确定m,n需要满足的条件;
(3)若l1⊥l2,试确定m,n需要满足的条件.
解:(1)将点P(m,-1)代入两直线方程得:m2-8+n=0和2m-m-1=0,解得m=1,n=7.
(2)由l1∥l2得:m2-8×2=0?m=±4,又两直线不能重合,所以有8×(-1)-nm≠0,对应得n≠±2,所以当m=4,n≠-2或m=-4,n≠2时,l1∥l2.
(3)当m=0时,直线l1:y=-和l2:x=,此时l1⊥l2,
当m≠0时,此时两直线的斜率之积等于,显然l1与l2不垂直,
所以当m=0,n∈R时直线l1和l2垂直.
19.(10分)已知直线l1:y=-k(x-a)和直线l2在x轴上的截距相等,且它们的倾斜角互补,且直线l1过点P(-3,3).如果点Q(2,2)到直线l2的距离为1,求l2的方程.
解:由题意,可设直线l2的方程为y=k(x-a),即kx-y-ak=0,
∵点Q(2,2)到直线l2的距离为1,
∴=1.①
又∵直线l1的方程为y=-k(x-a),且直线l1过点P(-3,3),∴ak=3-3k.②
由①②得=1,两边平方整理得12k2-25k+12=0,解得k=或k=,
∴当k=时,代入②得a=-,此时直线l2的方程为4x-3y+3=0;
当k=时,代入②得a=1,此时直线l2的方程为3x-4y-3=0.
综上所述,直线l2的方程为4x-3y+3=0或3x-4y-3=0.
20.(10分)在△ABC中,BC边上的高所在直线的方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0.若点B的坐标为(1,2),求点A和点C的坐标.
解:由方程组
解得点A的坐标为(-1,0).
又直线AB的斜率kAB=1,x轴是∠A的平分线,所以kAC=-1,则AC边所在的直线方程为y=-(x+1).①
又已知BC边上的高所在直线的方程为x-2y+1=0,故直线BC的斜率kBC=-2,
所以BC边所在的直线方程为y-2=-2(x-1).②
解①②组成的方程组得
即顶点C的坐标为(5,-6).
6
