2020-2021学年人教版八年级数学下册课件:第17章 勾股定理复习(22张)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册课件:第17章 勾股定理复习(22张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 708.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 00:00:00 | ||
图片预览






文档简介
复习课件
第十七章 勾股定理
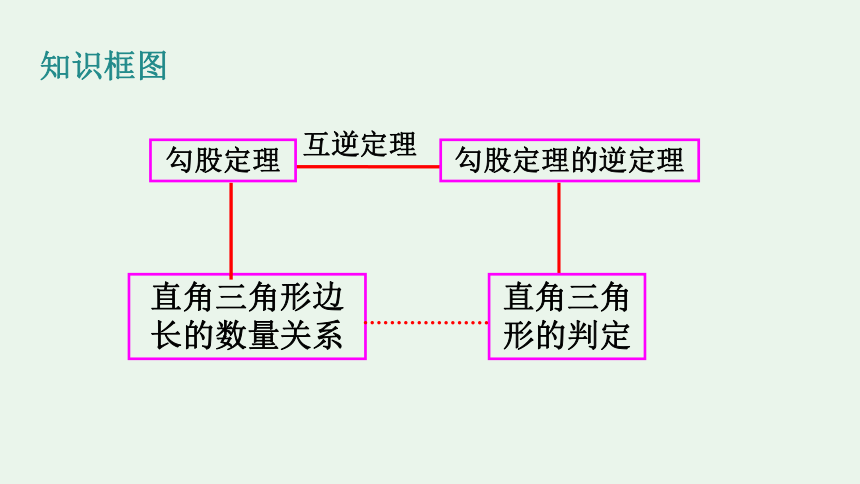
互逆定理
勾股定理
勾股定理的逆定理
直角三角形的判定
直角三角形边长的数量关系
知识框图
C
A
B
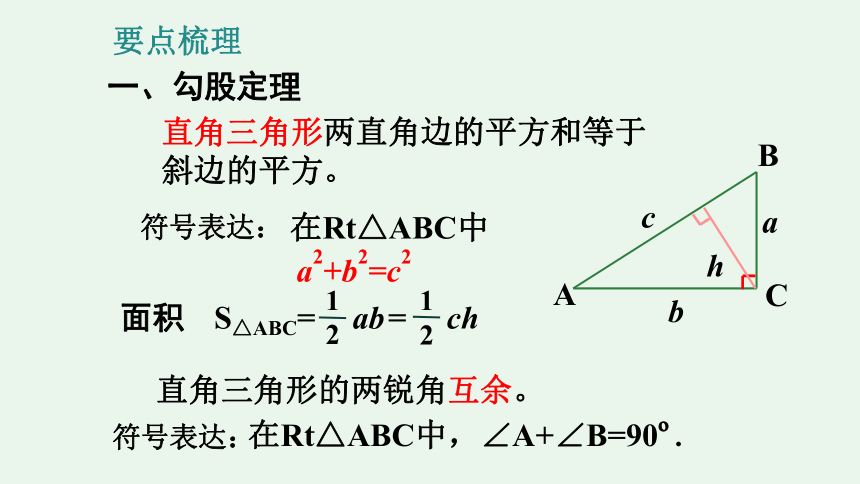
一、勾股定理
直角三角形两直角边的平方和等于
斜边的平方。
直角三角形的两锐角互余。
符号表达:
在Rt△ABC中,∠A+∠B=90?.
面积
符号表达:
在Rt△ABC中
a2+b2=c2
a
b
c
h
S△ABC= =
ab
1
2
ch
1
2
要点梳理
二、勾股定理的逆定理
1.勾股定理的逆定理
如果三角形的三边长a,b,c满足
a2 +b2=c2 ,那么这个三角形是直角三角形.
满足a2 +b2=c2的三个正整数,称为勾股数.
2.勾股数
3.原命题与逆命题
如果两个命题的题设、结论正好相反,那么把其中
一个叫做原命题,另一个叫做它的逆命题.
A
B
C
c
a
b
勾股定理
勾股定理的逆定理
题设
在Rt△ABC 中,∠C=900
在△ABC 中, 三边a,b,c满足a2+b2=c2
结论
a2+b2=c2
∠C=900
作用
1.用勾股定理进行计算
2.证明与平方有关的问题3.解决实际问题
1.判断某三角形是否为直角三角形(3种)
2.解决实际问题
联系
1.两个定理都与“三角形的三边关系a2+b2=c2”有关;
2.都与直角三角形有关;
3.都是数形结合思想的体现。
1.如图,已知在△ABC 中,∠B =90°,一直角边为a,斜边为b,则另一直角边c满足c2 = .
【思考】为什么不是 ?
答案:因为∠B 所对的边是斜边.
答案:
(一)知两边或一边一角型
题型一
勾股定理的直接应用
考题分类
2.如图,在边长为1个单位长度的小正方形组成的网格中,点A,B都是格点,则线段AB的长度为 ( )
A.5 B.6 C.7 D.25
3.在△ABC中,∠B=90°,a,b,c分别为∠A,∠B,∠C的对边.
(1)如果a=5,c=12,那么b= ;?
(2)如果b=61,a=60,那么c= .?
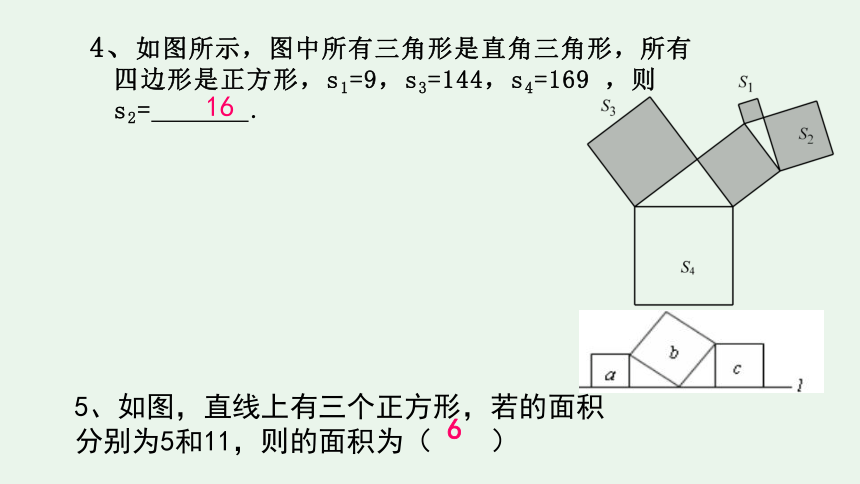
4、如图所示,图中所有三角形是直角三角形,所有四边形是正方形,s1=9,s3=144,s4=169 ,则s2= .
16
5、如图,直线上有三个正方形,若的面积分别为5和11,则的面积为( )
6
解:∵∠B=90°,∴b是斜边,
则在Rt△ABC中,由勾股定理,得
又∵S△ABC= b?BD= ac,
A
C
B
4
3
D
6. 在△ABC中,已知BD是高,∠B=90°,∠A、∠B、∠C的对边分别是a、b、c,且a=3,b=4,求BD的长.
7.已知一个直角三角形的两条边长是3 cm和4 cm,求第三条边的长.
注意:这里并没有指明已知的两条边就是直角边,所以4 cm可以是直角边,也可以是斜边,即应分情况讨论.
8.已知:在△ABC中,AB=15 cm,AC=13 cm,高AD=12 cm,求S△ABC.
8.如图,在Rt△ABC中,∠ABC=90°,AB=3,AC=5,点E在BC上,将△ABC沿AE折叠,使点B落在AC边上的点B′处,求BE的长.
8.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿 AC折叠,点D落在点D′处,求重叠部分△AFC的
面积.
解:易证△AFD′≌△CFB,
∴D′F=BF,
设D′F=x,则AF=8-x,
在Rt△AFD′中,(8-x)2=x2+42,
解得x=3.
∴AF=AB-FB=8-3=5,
∴S△AFC= AF?BC=10.
9.已知:如图,四边形ABCD,AB=1,BC=2,CD=2,AD=3, 且AB⊥BC.求四边形 ABCD的面积.
分析:本题解题的关键是恰当的添加辅助线,利用勾股定理的逆定理判定△ADC的形状为直角三角形,再利用勾股定理解题.
答案:连接AC,∵AB⊥BC,∴∠ABC=90°.
∵在△ABC中,∠ABC=90°,AB=1,BC=2,
∴AC= .∵CD=2,AD=3, ∴△ACD是直角三角形;∴四边形的面积为1+ .
考题分类
题型二
用勾股定理解决简单的实际问题
1.如图,透明的圆柱形容器(容器厚度忽略不计)的高为12 cm,底面周长为10 cm,在容器内壁离容器底部3 cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3 cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是____cm.
2.如图是一个三级台阶,它的每一级的长、宽和高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程是多少?
20
3
2
A
B
B
20
A
C
2
3
2
3
2
3
3. 在一块平地上,张大爷家屋前9米远处有一棵大树.在一次强风中,这棵大树从离地面6米处折断倒下,量得倒下部分的长是10米.出门在外的张大爷担心自己的房子被倒下的大树砸到.大树倒下时能砸到张大爷的房子吗?( )
A.一定不会 B.可能会
C.一定会 D.以上答案都不对
4. 如图,滑杆在机械槽内运动,∠ACB为直角,已知滑杆AB长2.5米,顶端A在AC上运动,量得滑杆下端B距C点的距离为1.5米,当端点B向右移动0.5米时,求滑杆顶端A下滑多少米?
A
E
C
B
D
答案:解:设AE的长为x 米,依题意
得CE=AC - x ,∵AB=DE=2.5,BC=1.5,
∠C=90°,∴AC=2.∵BD=0.5,∴AC=2.
∴在Rt△ECD中,CE=1.5.
∴2- x =1.5, x =0.5. 即AE=0.5 .
答:梯子下滑0.5米.
5.如图,某住宅社区在相邻两楼之间修建一个上方是一个
半圆,下方是长方形的仿古通道,现有一辆卡车装满家
具后,高4米,宽2.8米,请问这辆送家具的卡车能否通
过这个通道?
在Rt△ABO中,由题意知OA=2米,DC=OB=1.4米,
所以AB2=22-1.42=2.04.
因为4-2.6=1.4,1.42=1.96,
2.04>1.96,
所以卡车可以通过.
答:卡车可以通过,但要小心.
解:如图,过半圆直径的中点O,作直径的垂线交下底边于点D,取点C,使CD=1.4米,过C作OD的平行线交半圆直径于B点,交半圆于A点.
6.如图所示是一块地,已知AD=8米,CD=6米,∠D=900,AB=26米,BC=24 米,求这块地的面积。
C
7. 如图,一条河同一侧的两村庄A、B,其中A、B到河岸最短距离分别为AC=1km,BD=2km,CD=4km,现欲在河岸上M处建一个水泵站向A、B两村送水,当M在河岸上何处时,到A、B两村铺设水管总长度最短,并求出最短距离。
A
M
B
A′
D
E
1
2
4
1
1
4
5
勾
股
定
理
发现
应用
勾股
定理
证明
赵爽弦图
毕达哥拉斯
美国总统
在数轴上表示某些无理数
生活应用
旗杆、梯子、河水深度等问题
勾股定理的逆定理
内容
应用
已知三角形的三边长,判断是否是直角三角形
综合应用
折纸中的勾股定理
路程最短问题
拼图加面积法
猜想
直角三角形,已知两边,求第三边
勾股数
分类思想
特殊例子
用割、补法求图形面积
课堂小结
第十七章 勾股定理
互逆定理
勾股定理
勾股定理的逆定理
直角三角形的判定
直角三角形边长的数量关系
知识框图
C
A
B
一、勾股定理
直角三角形两直角边的平方和等于
斜边的平方。
直角三角形的两锐角互余。
符号表达:
在Rt△ABC中,∠A+∠B=90?.
面积
符号表达:
在Rt△ABC中
a2+b2=c2
a
b
c
h
S△ABC= =
ab
1
2
ch
1
2
要点梳理
二、勾股定理的逆定理
1.勾股定理的逆定理
如果三角形的三边长a,b,c满足
a2 +b2=c2 ,那么这个三角形是直角三角形.
满足a2 +b2=c2的三个正整数,称为勾股数.
2.勾股数
3.原命题与逆命题
如果两个命题的题设、结论正好相反,那么把其中
一个叫做原命题,另一个叫做它的逆命题.
A
B
C
c
a
b
勾股定理
勾股定理的逆定理
题设
在Rt△ABC 中,∠C=900
在△ABC 中, 三边a,b,c满足a2+b2=c2
结论
a2+b2=c2
∠C=900
作用
1.用勾股定理进行计算
2.证明与平方有关的问题3.解决实际问题
1.判断某三角形是否为直角三角形(3种)
2.解决实际问题
联系
1.两个定理都与“三角形的三边关系a2+b2=c2”有关;
2.都与直角三角形有关;
3.都是数形结合思想的体现。
1.如图,已知在△ABC 中,∠B =90°,一直角边为a,斜边为b,则另一直角边c满足c2 = .
【思考】为什么不是 ?
答案:因为∠B 所对的边是斜边.
答案:
(一)知两边或一边一角型
题型一
勾股定理的直接应用
考题分类
2.如图,在边长为1个单位长度的小正方形组成的网格中,点A,B都是格点,则线段AB的长度为 ( )
A.5 B.6 C.7 D.25
3.在△ABC中,∠B=90°,a,b,c分别为∠A,∠B,∠C的对边.
(1)如果a=5,c=12,那么b= ;?
(2)如果b=61,a=60,那么c= .?
4、如图所示,图中所有三角形是直角三角形,所有四边形是正方形,s1=9,s3=144,s4=169 ,则s2= .
16
5、如图,直线上有三个正方形,若的面积分别为5和11,则的面积为( )
6
解:∵∠B=90°,∴b是斜边,
则在Rt△ABC中,由勾股定理,得
又∵S△ABC= b?BD= ac,
A
C
B
4
3
D
6. 在△ABC中,已知BD是高,∠B=90°,∠A、∠B、∠C的对边分别是a、b、c,且a=3,b=4,求BD的长.
7.已知一个直角三角形的两条边长是3 cm和4 cm,求第三条边的长.
注意:这里并没有指明已知的两条边就是直角边,所以4 cm可以是直角边,也可以是斜边,即应分情况讨论.
8.已知:在△ABC中,AB=15 cm,AC=13 cm,高AD=12 cm,求S△ABC.
8.如图,在Rt△ABC中,∠ABC=90°,AB=3,AC=5,点E在BC上,将△ABC沿AE折叠,使点B落在AC边上的点B′处,求BE的长.
8.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿 AC折叠,点D落在点D′处,求重叠部分△AFC的
面积.
解:易证△AFD′≌△CFB,
∴D′F=BF,
设D′F=x,则AF=8-x,
在Rt△AFD′中,(8-x)2=x2+42,
解得x=3.
∴AF=AB-FB=8-3=5,
∴S△AFC= AF?BC=10.
9.已知:如图,四边形ABCD,AB=1,BC=2,CD=2,AD=3, 且AB⊥BC.求四边形 ABCD的面积.
分析:本题解题的关键是恰当的添加辅助线,利用勾股定理的逆定理判定△ADC的形状为直角三角形,再利用勾股定理解题.
答案:连接AC,∵AB⊥BC,∴∠ABC=90°.
∵在△ABC中,∠ABC=90°,AB=1,BC=2,
∴AC= .∵CD=2,AD=3, ∴△ACD是直角三角形;∴四边形的面积为1+ .
考题分类
题型二
用勾股定理解决简单的实际问题
1.如图,透明的圆柱形容器(容器厚度忽略不计)的高为12 cm,底面周长为10 cm,在容器内壁离容器底部3 cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3 cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是____cm.
2.如图是一个三级台阶,它的每一级的长、宽和高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程是多少?
20
3
2
A
B
B
20
A
C
2
3
2
3
2
3
3. 在一块平地上,张大爷家屋前9米远处有一棵大树.在一次强风中,这棵大树从离地面6米处折断倒下,量得倒下部分的长是10米.出门在外的张大爷担心自己的房子被倒下的大树砸到.大树倒下时能砸到张大爷的房子吗?( )
A.一定不会 B.可能会
C.一定会 D.以上答案都不对
4. 如图,滑杆在机械槽内运动,∠ACB为直角,已知滑杆AB长2.5米,顶端A在AC上运动,量得滑杆下端B距C点的距离为1.5米,当端点B向右移动0.5米时,求滑杆顶端A下滑多少米?
A
E
C
B
D
答案:解:设AE的长为x 米,依题意
得CE=AC - x ,∵AB=DE=2.5,BC=1.5,
∠C=90°,∴AC=2.∵BD=0.5,∴AC=2.
∴在Rt△ECD中,CE=1.5.
∴2- x =1.5, x =0.5. 即AE=0.5 .
答:梯子下滑0.5米.
5.如图,某住宅社区在相邻两楼之间修建一个上方是一个
半圆,下方是长方形的仿古通道,现有一辆卡车装满家
具后,高4米,宽2.8米,请问这辆送家具的卡车能否通
过这个通道?
在Rt△ABO中,由题意知OA=2米,DC=OB=1.4米,
所以AB2=22-1.42=2.04.
因为4-2.6=1.4,1.42=1.96,
2.04>1.96,
所以卡车可以通过.
答:卡车可以通过,但要小心.
解:如图,过半圆直径的中点O,作直径的垂线交下底边于点D,取点C,使CD=1.4米,过C作OD的平行线交半圆直径于B点,交半圆于A点.
6.如图所示是一块地,已知AD=8米,CD=6米,∠D=900,AB=26米,BC=24 米,求这块地的面积。
C
7. 如图,一条河同一侧的两村庄A、B,其中A、B到河岸最短距离分别为AC=1km,BD=2km,CD=4km,现欲在河岸上M处建一个水泵站向A、B两村送水,当M在河岸上何处时,到A、B两村铺设水管总长度最短,并求出最短距离。
A
M
B
A′
D
E
1
2
4
1
1
4
5
勾
股
定
理
发现
应用
勾股
定理
证明
赵爽弦图
毕达哥拉斯
美国总统
在数轴上表示某些无理数
生活应用
旗杆、梯子、河水深度等问题
勾股定理的逆定理
内容
应用
已知三角形的三边长,判断是否是直角三角形
综合应用
折纸中的勾股定理
路程最短问题
拼图加面积法
猜想
直角三角形,已知两边,求第三边
勾股数
分类思想
特殊例子
用割、补法求图形面积
课堂小结
