江苏省苏北四市(徐、连、宿、淮)2012届高三元月调研测试数学试题
文档属性
| 名称 | 江苏省苏北四市(徐、连、宿、淮)2012届高三元月调研测试数学试题 | 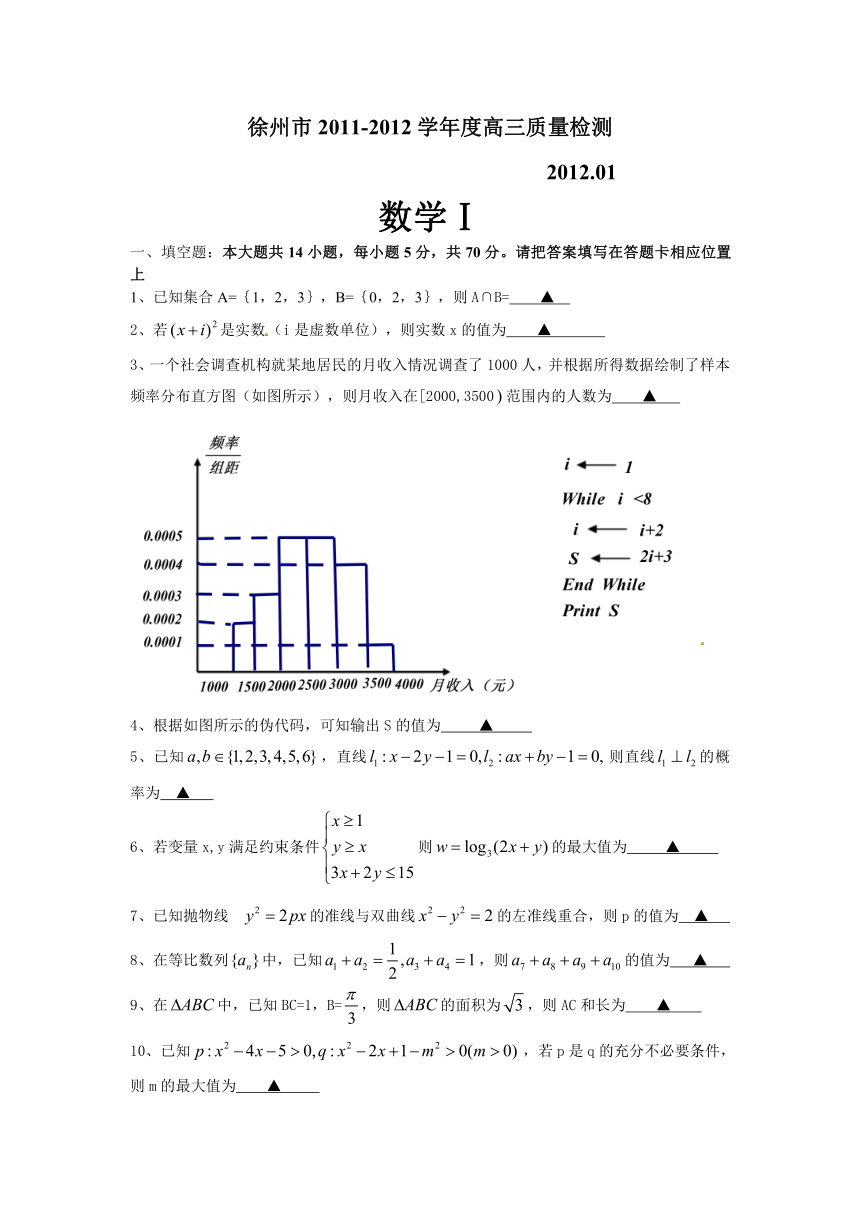 | |
| 格式 | zip | ||
| 文件大小 | 302.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-12 11:38:05 | ||
图片预览





文档简介
徐州市2011-2012学年度高三质量检测
2012.01
数学Ⅰ
一、填空题:本大题共14小题,每小题5分,共70分。请把答案填写在答题卡相应位置上
1、已知集合A={1,2,3},B={0,2,3},则A∩B= ▲
2、若是实数(i是虚数单位),则实数x的值为 ▲
3、一个社会调查机构就某地居民的月收入情况调查了1000人,并根据所得数据绘制了样本频率分布直方图(如图所示),则月收入在[2000,3500范围内的人数为 ▲
4、根据如图所示的伪代码,可知输出S的值为 ▲
5、已知,直线则直线的概率为 ▲
6、若变量x,y满足约束条件则的最大值为 ▲
7、已知抛物线的准线与双曲线的左准线重合,则p的值为 ▲
8、在等比数列中,已知,则的值为 ▲
9、在中,已知BC=1,B=,则的面积为,则AC和长为 ▲
10、已知,若p是q的充分不必要条件,则m的最大值为 ▲
11、已知椭圆的方程为,过椭圆的右焦点且与x轴垂直的直线与椭圆交于P、Q两点,椭圆的右准线与x轴交于点M,若为正三角形,则椭圆的离心率等于 ▲
12、函数图象上两相邻的最低点与最高点之间的最小值是 ▲
13、定义在R上的,满足且,则的值
为 ▲
14、已知函数若存在,当时,,则的取值范围是 ▲
二、解答题:本大题共6小题,共90分。请在答题卡指定的区域内作答,解答时应写出文字说明、求证过程或演算步骤
15.(本小题满分14分)
已知向量,求:
(1)
(2)的值。
16. (本小题满分14分)
如图,在直三棱柱中,AB=AC=5,BB1=BC=6,D,E分别是AA1和B1C的中点
求证:DE∥平面ABC;
求三棱锥E-BCD的体积。
17. (本小题满分14分)
现有一张长为80cm,宽为60cm的长方形铁皮ABCD,准备用它做成一只无盖长方体铁皮盒,要求材料利用率为100%,不考虑焊接处损失。如图,若长方形ABCD的一个角剪下一块铁皮,作为铁皮盒的底面,用余下材料剪拼后作为铁皮盒的侧面,设长方体的底面边长为x (cm),高为y (cm),体积为V (cm3)
求出x 与 y 的关系式;
求该铁皮盒体积V的最大值;
18. (本小题满分16分)
平面直角坐标系xoy中,直线截以原点O为圆心的圆所得的弦长为
(1)求圆O的方程;
(2)若直线与圆O切于第一象限,且与坐标轴交于D,E,当DE长最小时,求直线的方程;
(3)设M,P是圆O上任意两点,点M关于x轴的对称点为N,若直线MP、NP分别交于x轴于点
(m,0)和(n,0),问mn是否为定值?若是,请求出该定值;若不是,请说明理由。
19. (本小题满分16分)
已知函数,其中e是自然数的底数,。
当时,解不等式;
若在[-1,1]上是单调增函数,求的取值范围;
当时,求整数k的所有值,使方程在[k,k+1]上有解。
20. (本小题满分16分)
设数列的前n项和为,已知为常数,),eg
求p,q的值;
求数列的通项公式;
是否存在正整数m,n,使成立?若存在,求出所有符合条件的有序实数对(m,n);若不存在,说明理由。
徐州市2011-2012学年度高三第一次质量检测
数学Ⅱ(附加题)
21.【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,
若多做,则按作答的前两题评分。解答时应写出文字说明、证明过程或演算步骤.
选修4-1:几何证明选讲(本小题满分10分)
如图,是直角,圆O与AP相切于点T,与AQ相交于两点B,C。求证:BT平分
选修4-2:矩阵与变换(本小题满分10分)
若点A(2,2)在矩阵对应变换的作用下得到的点为B(-2,2),求矩阵M的逆矩阵
选修4-2:矩阵与变换(本小题满分10分)
在极坐标系中,A为曲线上的动点,B为直线上的动点,求AB的最小值。
D.选修4-5:不等式选讲(本小题满分10分)
已知都是正数,且=1,求证:
【必做题】第22题、第23题,每题10分,共计20分.请在答题卡指定区域内作答,解答时应写出
文字说明、证明过程或演算步骤。
22. (本小题满分10分)
如图,已知面积为1的正三角形ABC三边的中点分别为D、E、F,从A,B,C,D,E,F六个点中任取三个不同的点,所构成的三角形的面积为X(三点共线时,规定X=0)
求;
求E(X)
23.(本小题满分10分)
如图,过抛物线上一点P(1,-2)作倾斜角互补的两条直线,分别与抛物线交于点
求的值;
若,求面积的最大值。
徐州市2012年高三年级质量检测
数学Ⅰ参考答案与评分标准
一、填空题
1.; 2.0 ; 3.650; 4.21; 5.; 6.2; 7.2 ; 8.12;
9.; 10.2; 11.; 12.; 13.1006; 14. .
二、解答题:
15.⑴因为,所以,………………………2分
解得 ,又因为,………………………………………4分
所以,, ………………………………………6分
所以,因此 .………………………8分
⑵…………………………………12分
.…………………………………………………14分
16.⑴取BC中点G,连接AG,EG,
因为是的中点,所以EG∥,
且.
由直棱柱知,,而是的中点,
所以,…………………………4分
所以四边形是平行四边形,
所以,又平面,
所以∥平面. ………………………7分
⑵因为,所以平面,
所以,………………………………………10分
由⑴知,∥平面,
所以.…………………14分
17.⑴由题意得,
即,. ……………………………………………6分
⑵铁皮盒体积,………………10分
,令,得, ……………………………12分
因为,,是增函数;
,,是减函数,
所以,在时取得极大值,也是最大值,其值为.
答:该铁皮盒体积的最大值是. ……………………14分
18.⑴因为点到直线的距离为, ………………………2分
所以圆的半径为,
故圆的方程为. ………………4分
⑵设直线的方程为,即,
由直线与圆相切,得,即, ……………6分
,
当且仅当时取等号,此时直线的方程为.………10分
⑶设,,则,,,
直线与轴交点,,
直线与轴交点,, …………………14分
,
故为定值2. …………………16分
19.⑴因为,所以不等式即为,
又因为,所以不等式可化为,
所以不等式的解集为.………………………………………4分
⑵,
①当时,,在上恒成立,当且仅当时
取等号,故符合要求;………………………………………………………6分
②当时,令,因为,
所以有两个不相等的实数根,,不妨设,
因此有极大值又有极小值.
若,因为,所以在内有极值点,
故在上不单调.………………………………………………………8分
若,可知,
因为的图象开口向下,要使在上单调,因为,
必须满足即所以.
综上可知,的取值范围是.………………………………………10分
⑶当时, 方程即为,由于,所以不是方程的解,
所以原方程等价于,令,
因为对于恒成立,
所以在和内是单调增函数,……………………………13分
又,,,,
所以方程有且只有两个实数根,且分别在区间和上,
所以整数的所有值为.………………………………………………………16分
20.⑴由题意,知即解之得 …………… 4分
⑵由⑴知,,①
当时,,②
①②得,,…………………………………………………… 6分
又,所以,所以是首项为,公比为的等比数列,
所以.…………………………………………………………………… 8分
⑶由⑵得,,由,得
,即,……………………… 10分
即,因为,所以,
所以,且,
因为,所以或或.……………………………………………… 12分
当时,由得,,所以;
当时,由得,,所以或;
当时,由得,,所以或或,
综上可知,存在符合条件的所有有序实数对为:
.…………………………………………… 16分
徐州市2012年高三年级质量检测
数学Ⅱ(附加题)参考答案与评分标准
21.
A.连结,因为是切线,所以.又因为是直角,即,所以,所以.……………………………… 5分
又,所以,
所以,
即平分.……………………………… 10分
B.由题意知, ,即 ,
所以 解得所以.………………5分
由,解得. …………………………………10分
另解:矩阵的行列式,所以.
C.圆方程为,圆心,直线方程为,…… 5分
圆心到直线的距离,所以. ………… 10分
D.因为是正数,所以, ……………………………5分
同理,
将上述不等式两边相乘,得 ,
因为,所以.………………………10分
22.⑴从六点中任取三个不同的点共有个基本事件,
事件“”所含基本事件有,
从而.……………………………………………………………5分
⑵的分布列为:
则.
答:,.…………………………………………10分
23.⑴因为,在抛物线上,
所以, ,
同理,依题有,
因为,所以. ……………………………4分
⑵由⑴知,设的方程为,
到的距离为,,
所以=
, …………………………………………………8分
令,由,,可知.,
因为为偶函数,只考虑的情况,
记,,故在是单调增函数,故的最大值为,故的最大值为6.……………………10分
(第16题)
·
(第21-A题)
2012.01
数学Ⅰ
一、填空题:本大题共14小题,每小题5分,共70分。请把答案填写在答题卡相应位置上
1、已知集合A={1,2,3},B={0,2,3},则A∩B= ▲
2、若是实数(i是虚数单位),则实数x的值为 ▲
3、一个社会调查机构就某地居民的月收入情况调查了1000人,并根据所得数据绘制了样本频率分布直方图(如图所示),则月收入在[2000,3500范围内的人数为 ▲
4、根据如图所示的伪代码,可知输出S的值为 ▲
5、已知,直线则直线的概率为 ▲
6、若变量x,y满足约束条件则的最大值为 ▲
7、已知抛物线的准线与双曲线的左准线重合,则p的值为 ▲
8、在等比数列中,已知,则的值为 ▲
9、在中,已知BC=1,B=,则的面积为,则AC和长为 ▲
10、已知,若p是q的充分不必要条件,则m的最大值为 ▲
11、已知椭圆的方程为,过椭圆的右焦点且与x轴垂直的直线与椭圆交于P、Q两点,椭圆的右准线与x轴交于点M,若为正三角形,则椭圆的离心率等于 ▲
12、函数图象上两相邻的最低点与最高点之间的最小值是 ▲
13、定义在R上的,满足且,则的值
为 ▲
14、已知函数若存在,当时,,则的取值范围是 ▲
二、解答题:本大题共6小题,共90分。请在答题卡指定的区域内作答,解答时应写出文字说明、求证过程或演算步骤
15.(本小题满分14分)
已知向量,求:
(1)
(2)的值。
16. (本小题满分14分)
如图,在直三棱柱中,AB=AC=5,BB1=BC=6,D,E分别是AA1和B1C的中点
求证:DE∥平面ABC;
求三棱锥E-BCD的体积。
17. (本小题满分14分)
现有一张长为80cm,宽为60cm的长方形铁皮ABCD,准备用它做成一只无盖长方体铁皮盒,要求材料利用率为100%,不考虑焊接处损失。如图,若长方形ABCD的一个角剪下一块铁皮,作为铁皮盒的底面,用余下材料剪拼后作为铁皮盒的侧面,设长方体的底面边长为x (cm),高为y (cm),体积为V (cm3)
求出x 与 y 的关系式;
求该铁皮盒体积V的最大值;
18. (本小题满分16分)
平面直角坐标系xoy中,直线截以原点O为圆心的圆所得的弦长为
(1)求圆O的方程;
(2)若直线与圆O切于第一象限,且与坐标轴交于D,E,当DE长最小时,求直线的方程;
(3)设M,P是圆O上任意两点,点M关于x轴的对称点为N,若直线MP、NP分别交于x轴于点
(m,0)和(n,0),问mn是否为定值?若是,请求出该定值;若不是,请说明理由。
19. (本小题满分16分)
已知函数,其中e是自然数的底数,。
当时,解不等式;
若在[-1,1]上是单调增函数,求的取值范围;
当时,求整数k的所有值,使方程在[k,k+1]上有解。
20. (本小题满分16分)
设数列的前n项和为,已知为常数,),eg
求p,q的值;
求数列的通项公式;
是否存在正整数m,n,使成立?若存在,求出所有符合条件的有序实数对(m,n);若不存在,说明理由。
徐州市2011-2012学年度高三第一次质量检测
数学Ⅱ(附加题)
21.【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,
若多做,则按作答的前两题评分。解答时应写出文字说明、证明过程或演算步骤.
选修4-1:几何证明选讲(本小题满分10分)
如图,是直角,圆O与AP相切于点T,与AQ相交于两点B,C。求证:BT平分
选修4-2:矩阵与变换(本小题满分10分)
若点A(2,2)在矩阵对应变换的作用下得到的点为B(-2,2),求矩阵M的逆矩阵
选修4-2:矩阵与变换(本小题满分10分)
在极坐标系中,A为曲线上的动点,B为直线上的动点,求AB的最小值。
D.选修4-5:不等式选讲(本小题满分10分)
已知都是正数,且=1,求证:
【必做题】第22题、第23题,每题10分,共计20分.请在答题卡指定区域内作答,解答时应写出
文字说明、证明过程或演算步骤。
22. (本小题满分10分)
如图,已知面积为1的正三角形ABC三边的中点分别为D、E、F,从A,B,C,D,E,F六个点中任取三个不同的点,所构成的三角形的面积为X(三点共线时,规定X=0)
求;
求E(X)
23.(本小题满分10分)
如图,过抛物线上一点P(1,-2)作倾斜角互补的两条直线,分别与抛物线交于点
求的值;
若,求面积的最大值。
徐州市2012年高三年级质量检测
数学Ⅰ参考答案与评分标准
一、填空题
1.; 2.0 ; 3.650; 4.21; 5.; 6.2; 7.2 ; 8.12;
9.; 10.2; 11.; 12.; 13.1006; 14. .
二、解答题:
15.⑴因为,所以,………………………2分
解得 ,又因为,………………………………………4分
所以,, ………………………………………6分
所以,因此 .………………………8分
⑵…………………………………12分
.…………………………………………………14分
16.⑴取BC中点G,连接AG,EG,
因为是的中点,所以EG∥,
且.
由直棱柱知,,而是的中点,
所以,…………………………4分
所以四边形是平行四边形,
所以,又平面,
所以∥平面. ………………………7分
⑵因为,所以平面,
所以,………………………………………10分
由⑴知,∥平面,
所以.…………………14分
17.⑴由题意得,
即,. ……………………………………………6分
⑵铁皮盒体积,………………10分
,令,得, ……………………………12分
因为,,是增函数;
,,是减函数,
所以,在时取得极大值,也是最大值,其值为.
答:该铁皮盒体积的最大值是. ……………………14分
18.⑴因为点到直线的距离为, ………………………2分
所以圆的半径为,
故圆的方程为. ………………4分
⑵设直线的方程为,即,
由直线与圆相切,得,即, ……………6分
,
当且仅当时取等号,此时直线的方程为.………10分
⑶设,,则,,,
直线与轴交点,,
直线与轴交点,, …………………14分
,
故为定值2. …………………16分
19.⑴因为,所以不等式即为,
又因为,所以不等式可化为,
所以不等式的解集为.………………………………………4分
⑵,
①当时,,在上恒成立,当且仅当时
取等号,故符合要求;………………………………………………………6分
②当时,令,因为,
所以有两个不相等的实数根,,不妨设,
因此有极大值又有极小值.
若,因为,所以在内有极值点,
故在上不单调.………………………………………………………8分
若,可知,
因为的图象开口向下,要使在上单调,因为,
必须满足即所以.
综上可知,的取值范围是.………………………………………10分
⑶当时, 方程即为,由于,所以不是方程的解,
所以原方程等价于,令,
因为对于恒成立,
所以在和内是单调增函数,……………………………13分
又,,,,
所以方程有且只有两个实数根,且分别在区间和上,
所以整数的所有值为.………………………………………………………16分
20.⑴由题意,知即解之得 …………… 4分
⑵由⑴知,,①
当时,,②
①②得,,…………………………………………………… 6分
又,所以,所以是首项为,公比为的等比数列,
所以.…………………………………………………………………… 8分
⑶由⑵得,,由,得
,即,……………………… 10分
即,因为,所以,
所以,且,
因为,所以或或.……………………………………………… 12分
当时,由得,,所以;
当时,由得,,所以或;
当时,由得,,所以或或,
综上可知,存在符合条件的所有有序实数对为:
.…………………………………………… 16分
徐州市2012年高三年级质量检测
数学Ⅱ(附加题)参考答案与评分标准
21.
A.连结,因为是切线,所以.又因为是直角,即,所以,所以.……………………………… 5分
又,所以,
所以,
即平分.……………………………… 10分
B.由题意知, ,即 ,
所以 解得所以.………………5分
由,解得. …………………………………10分
另解:矩阵的行列式,所以.
C.圆方程为,圆心,直线方程为,…… 5分
圆心到直线的距离,所以. ………… 10分
D.因为是正数,所以, ……………………………5分
同理,
将上述不等式两边相乘,得 ,
因为,所以.………………………10分
22.⑴从六点中任取三个不同的点共有个基本事件,
事件“”所含基本事件有,
从而.……………………………………………………………5分
⑵的分布列为:
则.
答:,.…………………………………………10分
23.⑴因为,在抛物线上,
所以, ,
同理,依题有,
因为,所以. ……………………………4分
⑵由⑴知,设的方程为,
到的距离为,,
所以=
, …………………………………………………8分
令,由,,可知.,
因为为偶函数,只考虑的情况,
记,,故在是单调增函数,故的最大值为,故的最大值为6.……………………10分
(第16题)
·
(第21-A题)
同课章节目录
