2020-2021学年苏科版数学七年级下册9.4 乘法公式 提优训练(word版含答案)
文档属性
| 名称 | 2020-2021学年苏科版数学七年级下册9.4 乘法公式 提优训练(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 875.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 00:00:00 | ||
图片预览




文档简介
9.4 乘法公式 提优训练
一、单选题
1.(2020·浙江杭州市·七年级期末)下列各式不能用平方差公式计算的是( )
A. B.
C. D.
2.(2020·重庆开州区·八年级期末)计算的结果为( )
A. B. C. D.
3.(2021·江西宜春市·八年级期末)图(1)是一个长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,小长方形的长为,宽为,然后按图(2)拼成一个正方形,通过计算,用拼接前后两个图形中阴影部分的面积可以验证的等式是( )
A. B.
C. D.
4.(2021·福建泉州市·八年级期末)已知x的二次三项式可以写成一个完全平方式,则k的值是( )
A.3 B. C.6 D.
5.(2020·浙江金华市·七年级期中)若是完全平方式,则m的值为( )
A.4 B.2或 C. D.或4
6.(2021·河北衡水市·八年级期末)将变形正确的是( )
A. B.
C. D.
7.(2020·浙江杭州市·七年级其他模拟)若是完全平方式,与的乘积中不含x的一次项,则的值为( )
A.-4 B.16 C.-4或-16 D.4或16
8.(2020·浙江杭州市·七年级期中)已知,,则的值为( )
A.3 B.6 C.12 D.18
9.(2021·河南三门峡市·八年级期末)已知,,则的值是( )
A.64 B.52 C.50 D.28
10.(2021·安徽芜湖市·八年级期末)己知,则的值为( )
A.6 B.7 C.9 D.11
11.(2021·贵州遵义市·八年级期末)若的值为,则的值为( )
A. B. C. D.
12.(2020·浙江杭州市·七年级期中)己知,,则M,N的大小关系为( )
A. B. C. D.不能确定
13.(2020·全国八年级单元测试)已知,则的值为( )
A. B. C. D.
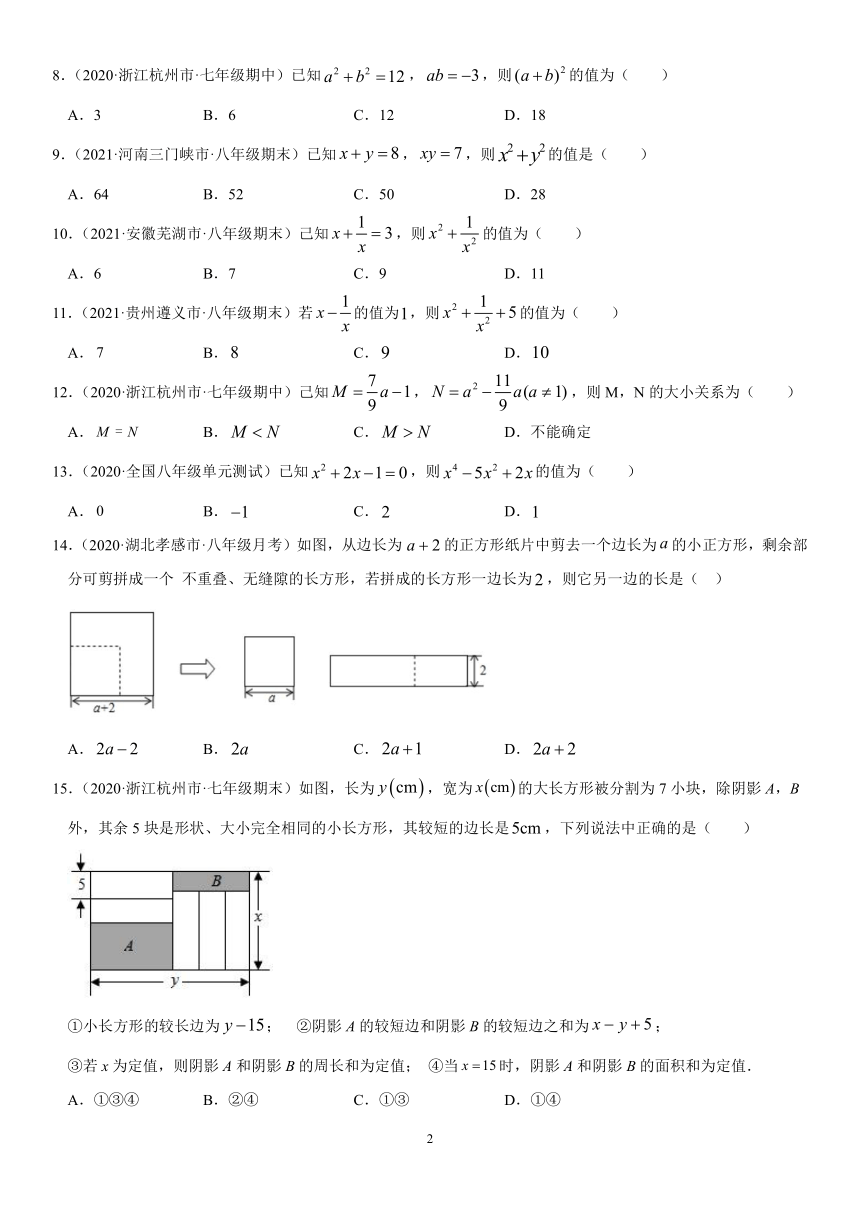
14.(2020·湖北孝感市·八年级月考)如图,从边长为的正方形纸片中剪去一个边长为的小正方形,剩余部分可剪拼成一个 不重叠、无缝隙的长方形,若拼成的长方形一边长为,则它另一边的长是( )
A. B. C. D.
15.(2020·浙江杭州市·七年级期末)如图,长为,宽为的大长方形被分割为7小块,除阴影A,B外,其余5块是形状、大小完全相同的小长方形,其较短的边长是,下列说法中正确的是( )
①小长方形的较长边为; ②阴影A的较短边和阴影B的较短边之和为;
③若x为定值,则阴影A和阴影B的周长和为定值; ④当时,阴影A和阴影B的面积和为定值.
A.①③④ B.②④ C.①③ D.①④
16.(2020·河南郑州市·八年级月考)如图,麦麦用9张A类正方形卡片、1张B类正方形卡片和6张C类长方形卡片,拼成了一个大正方形,拼成的大正方形的边长是( )
A. B. C. D.
17.(2020·孝感市孝南区肖港镇肖港初级中学八年级月考)算式(2+1)×(22+1)×(24+1)×…×(232+1)+1计算结果的个位数字是(?? )
A.8 B.6 C.4 D.2
二、填空题
18.(2021·福建龙岩市·九年级期末)______=______.
19.(2020·河南南阳市·八年级期末)计算:______________.
20.(2021·河南周口市·八年级期末)如果是完全平方式,则的值是___________________.
21.(2021·吉林延边朝鲜族自治州·八年级期末)若,,则_________.
22.(2021·重庆渝北区·八年级期末)已知,,则______.
23.(2020·余干县第三中学八年级月考)已知,,则ab=________
24.(2020·浙江杭州市·七年级其他模拟)若,,则__________.
25.(2021·山东临沂市·八年级期末)若,则____________
26.(2021·四川绵阳市·八年级期末)如图,一块直径为的圆形彩色纸板,从中挖去直径分别为与的两个小圆,若,,则剩下的纸板的面积是_______.
27.(2021·福建泉州市·八年级期末)如图所示,将一个边长为a的正方形减去一个边长为b的小正方形,将剩余部分(阴影部分)对半剪开,恰好是两个完全相同的直角梯形,将它们旋转拼接后构成一个等腰梯形.
(1)利用图形的面积关系可以得到一个代数恒等式是________;
(2)求前n个正奇数1,3,5,7,…的和是________.
28.(2021·广东广州市·绿翠现代实验学校八年级期末)已知a+b=5,且ab=3,则a3+b3=_____.
29.(2020·浙江杭州市·七年级期中)记,且,则__________.
30.(2020·浙江杭州市·七年级其他模拟)的值为_______.
31.(2020·浙江杭州市·七年级期末)当取______时,取______时,多项式取得最小值是______.
32.(2020·江苏南通市·八年级期末)已知实数,满足,,则_______.
33.(2019·西安市铁一中学七年级期中)已知,则________.
34.(2019·宜兴市新芳中学七年级期中)已知,,,则代数式2(a2+b2+c2-ab-bc-ca)=___________.
三、解答题
35.(2021·湖北武汉市·八年级期末)整式的计算:
(1)
(2)
36.(2019·李达中学七年级月考)用简便方法计算
(1) (2)
37.(2021·重庆梁平区·八年级期末)先化简,再求值:
(1)6x2y(﹣2xy+y3)÷xy2,其中x=2,y=﹣1;
(2)(x+2y)(x﹣2y)+(x﹣2y)2﹣(6x2y﹣2xy2)÷(2y),其中x=﹣2,y=.
38.(2021·广东广州市·八年级期末)已知(a+b)2=25,(a﹣b)2=9.求a2﹣6ab+b2.
39.(2019·上海市松江九峰实验学校)已知,求和的值.
40.(2021·湖北襄阳市·八年级期末)如图1是一个长为、宽为的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2).
(1)观察图2请你写出、、之间的等量关系是______;
(2)拓展应用:若,求的值.
41.(2021·山西晋城市·八年级期末)阅读下面材料,完成任务.
多项式除以多项式可以类比于多位数的除法进行计算,先把多项式按照某个字母的降幂进行排列,缺少的项可以看做系数为零,然后类比多位数的除法利用竖式进行计算.
∴ ∴
请用以上方法解决下列问题:(计算过程要有竖式)
(1)计算:
(2)若关于的多项式能被二项式整除,且,均为自然数,求满足以上条件的,的值.
42.(2019·福建厦门市·八年级月考)教科书中这样写道:“我们把多项式及叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,可以求代数式的最大值或最小值等.
例如:求代数式的最小值.
当时,有最小值,最小值是.
根据阅读材料用配方法解决下列问题:
(1)当为何值时,代数式有最小值,求出这个最小值.
(2)当,为什么关系时,代数式有最小值,并求出这个最小值.
(3)当,为何值时,多项式有最大值,并求出这个最大值.
43.(2020·浙江杭州市·七年级其他模拟)图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)你认为图2中的阴影部分的正方形的边长等于______;
(2)请用两种不同的方法求图2中阴影部分的面积.
①________________;
②__________________.
(3)观察图2你能写出,,三个代数式之间的等量_____________.
(4)运用你所得到的公式,计算若知,求和的值.
(5)用完全平方公式和非负数的性质求代数式的最小值.
44.(2021·山东滨州市·八年级期末)(知识生成)
我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式,例如图1可以得到,基于此,请解答下列问题:
(1)根据图2,写出一个代数恒等式:_________.
(2)利用(1)中得到的结论,解决下面的问题:若,,则__________.
(3)小明同学用图3中张边长为的正方形,张边长为的正方形,张宽、长分别为、的长方形纸片拼出一个面积为长方形,则_________.
(知识迁移)
(4)事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图4表示的是一个边长为的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式:_________.
参考答案
1.D 2.B 3.B 4.D 5.D 6.C 7.D 8.B 9.C 10.B
11.B 12.B 13.A 14.D 15.C 16.D 17.B
18.36 6 19.250000 20. 21.1 22.29 23.1 24.8
25.0 26. 27. 28.80 29.64
30. 31.2 -5 5 32.-1 33.7 34.6
35.(1);(2)
【详解】
解:(1)
(2)
36.(1)10000;(2).
【详解】
解:(1)===10000.
(2)
=
=
=
=
=
=.
37.(1),;(2),
【详解】
解:(1)原式=,
把x=2,y=-1代入得:原式=;
(2)原式=,
把x=﹣2,y=代入得:原式=.
38.﹣7
【详解】
解:因为(a+b)2=25,(a﹣b)2=9,
所以(a﹣b)2﹣(a﹣b)2=4ab=16,
所以a2﹣6ab+b2=(a﹣b)2﹣4ab=9﹣16=﹣7.
39.5;47
【详解】
;
∵,
∴,即,
∴
40.(1);(2).
【详解】
解:(1)
(2)令,,
则,
由
∴
∴
即.
41.(1);(2),;,;,
【详解】
解:(1)列竖式如下:
(2)列竖式如下:
∵多项式能被二项式整除
∴余式
∵,均为自然数
∴,;,;,
42.(1)代数式有最小值为1;(2)代数式有最小值为3.(3)当,时,多项式有最大值为17.
【详解】
(1)原式
当时,代数式有最小值为1;
(2)原式
代数式有最小值为3.
(3)原式
当,时,多项式有最大值为17.
43.(1)m-n;(2)①(m-n)2;②(m+n)2-4mn;(3)(m-n)2=(m+n)2-4mn;(4),=±48;(5)3
【详解】
解:(1)由图可知,阴影部分小正方形的边长为:m-n;
(2)根据正方形的面积公式,阴影部分的面积为(m-n)2,
还可以表示为(m+n)2-4mn;
(3)根据阴影部分的面积相等,(m-n)2=(m+n)2-4mn;
(4)∵,
∴==36,
∴,
若,则===48,
若,则===-48;
(5)
=
=
∵,,
∴≥3,即最小值为3.
44.(1);(2)30;(3)16;(4).
【详解】
(1)由图2得:正方形的面积=(a+b+c)2;正方形的面积=a2+b2+c2+2ab+2ac+2bc,
∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,
故答案为:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
(2)∵(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,
∵a+b+c=10,ab+ac+bc=35,
∴102=a2+b2+c2+2×35,
∴a2+b2+c2=100-70=30,
故答案为:30;
(3)由题意得:(3a+b)(a+3b)=xa2+yb2+zab,
∴3a2+10ab+3b2=xa2+yb2+zab,
∴x=3,y=3,z=10,
∴x+y+z=16,
故答案为:16;
(4)∵原几何体的体积=x3-1×1?x=x3-x,新几何体的体积= x(x+1)(x-1),
∴x3-x= x(x+1)(x-1).
故答案为:x3-x=x(x+1)(x-1).
一、单选题
1.(2020·浙江杭州市·七年级期末)下列各式不能用平方差公式计算的是( )
A. B.
C. D.
2.(2020·重庆开州区·八年级期末)计算的结果为( )
A. B. C. D.
3.(2021·江西宜春市·八年级期末)图(1)是一个长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,小长方形的长为,宽为,然后按图(2)拼成一个正方形,通过计算,用拼接前后两个图形中阴影部分的面积可以验证的等式是( )
A. B.
C. D.
4.(2021·福建泉州市·八年级期末)已知x的二次三项式可以写成一个完全平方式,则k的值是( )
A.3 B. C.6 D.
5.(2020·浙江金华市·七年级期中)若是完全平方式,则m的值为( )
A.4 B.2或 C. D.或4
6.(2021·河北衡水市·八年级期末)将变形正确的是( )
A. B.
C. D.
7.(2020·浙江杭州市·七年级其他模拟)若是完全平方式,与的乘积中不含x的一次项,则的值为( )
A.-4 B.16 C.-4或-16 D.4或16
8.(2020·浙江杭州市·七年级期中)已知,,则的值为( )
A.3 B.6 C.12 D.18
9.(2021·河南三门峡市·八年级期末)已知,,则的值是( )
A.64 B.52 C.50 D.28
10.(2021·安徽芜湖市·八年级期末)己知,则的值为( )
A.6 B.7 C.9 D.11
11.(2021·贵州遵义市·八年级期末)若的值为,则的值为( )
A. B. C. D.
12.(2020·浙江杭州市·七年级期中)己知,,则M,N的大小关系为( )
A. B. C. D.不能确定
13.(2020·全国八年级单元测试)已知,则的值为( )
A. B. C. D.
14.(2020·湖北孝感市·八年级月考)如图,从边长为的正方形纸片中剪去一个边长为的小正方形,剩余部分可剪拼成一个 不重叠、无缝隙的长方形,若拼成的长方形一边长为,则它另一边的长是( )
A. B. C. D.
15.(2020·浙江杭州市·七年级期末)如图,长为,宽为的大长方形被分割为7小块,除阴影A,B外,其余5块是形状、大小完全相同的小长方形,其较短的边长是,下列说法中正确的是( )
①小长方形的较长边为; ②阴影A的较短边和阴影B的较短边之和为;
③若x为定值,则阴影A和阴影B的周长和为定值; ④当时,阴影A和阴影B的面积和为定值.
A.①③④ B.②④ C.①③ D.①④
16.(2020·河南郑州市·八年级月考)如图,麦麦用9张A类正方形卡片、1张B类正方形卡片和6张C类长方形卡片,拼成了一个大正方形,拼成的大正方形的边长是( )
A. B. C. D.
17.(2020·孝感市孝南区肖港镇肖港初级中学八年级月考)算式(2+1)×(22+1)×(24+1)×…×(232+1)+1计算结果的个位数字是(?? )
A.8 B.6 C.4 D.2
二、填空题
18.(2021·福建龙岩市·九年级期末)______=______.
19.(2020·河南南阳市·八年级期末)计算:______________.
20.(2021·河南周口市·八年级期末)如果是完全平方式,则的值是___________________.
21.(2021·吉林延边朝鲜族自治州·八年级期末)若,,则_________.
22.(2021·重庆渝北区·八年级期末)已知,,则______.
23.(2020·余干县第三中学八年级月考)已知,,则ab=________
24.(2020·浙江杭州市·七年级其他模拟)若,,则__________.
25.(2021·山东临沂市·八年级期末)若,则____________
26.(2021·四川绵阳市·八年级期末)如图,一块直径为的圆形彩色纸板,从中挖去直径分别为与的两个小圆,若,,则剩下的纸板的面积是_______.
27.(2021·福建泉州市·八年级期末)如图所示,将一个边长为a的正方形减去一个边长为b的小正方形,将剩余部分(阴影部分)对半剪开,恰好是两个完全相同的直角梯形,将它们旋转拼接后构成一个等腰梯形.
(1)利用图形的面积关系可以得到一个代数恒等式是________;
(2)求前n个正奇数1,3,5,7,…的和是________.
28.(2021·广东广州市·绿翠现代实验学校八年级期末)已知a+b=5,且ab=3,则a3+b3=_____.
29.(2020·浙江杭州市·七年级期中)记,且,则__________.
30.(2020·浙江杭州市·七年级其他模拟)的值为_______.
31.(2020·浙江杭州市·七年级期末)当取______时,取______时,多项式取得最小值是______.
32.(2020·江苏南通市·八年级期末)已知实数,满足,,则_______.
33.(2019·西安市铁一中学七年级期中)已知,则________.
34.(2019·宜兴市新芳中学七年级期中)已知,,,则代数式2(a2+b2+c2-ab-bc-ca)=___________.
三、解答题
35.(2021·湖北武汉市·八年级期末)整式的计算:
(1)
(2)
36.(2019·李达中学七年级月考)用简便方法计算
(1) (2)
37.(2021·重庆梁平区·八年级期末)先化简,再求值:
(1)6x2y(﹣2xy+y3)÷xy2,其中x=2,y=﹣1;
(2)(x+2y)(x﹣2y)+(x﹣2y)2﹣(6x2y﹣2xy2)÷(2y),其中x=﹣2,y=.
38.(2021·广东广州市·八年级期末)已知(a+b)2=25,(a﹣b)2=9.求a2﹣6ab+b2.
39.(2019·上海市松江九峰实验学校)已知,求和的值.
40.(2021·湖北襄阳市·八年级期末)如图1是一个长为、宽为的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2).
(1)观察图2请你写出、、之间的等量关系是______;
(2)拓展应用:若,求的值.
41.(2021·山西晋城市·八年级期末)阅读下面材料,完成任务.
多项式除以多项式可以类比于多位数的除法进行计算,先把多项式按照某个字母的降幂进行排列,缺少的项可以看做系数为零,然后类比多位数的除法利用竖式进行计算.
∴ ∴
请用以上方法解决下列问题:(计算过程要有竖式)
(1)计算:
(2)若关于的多项式能被二项式整除,且,均为自然数,求满足以上条件的,的值.
42.(2019·福建厦门市·八年级月考)教科书中这样写道:“我们把多项式及叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,可以求代数式的最大值或最小值等.
例如:求代数式的最小值.
当时,有最小值,最小值是.
根据阅读材料用配方法解决下列问题:
(1)当为何值时,代数式有最小值,求出这个最小值.
(2)当,为什么关系时,代数式有最小值,并求出这个最小值.
(3)当,为何值时,多项式有最大值,并求出这个最大值.
43.(2020·浙江杭州市·七年级其他模拟)图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)你认为图2中的阴影部分的正方形的边长等于______;
(2)请用两种不同的方法求图2中阴影部分的面积.
①________________;
②__________________.
(3)观察图2你能写出,,三个代数式之间的等量_____________.
(4)运用你所得到的公式,计算若知,求和的值.
(5)用完全平方公式和非负数的性质求代数式的最小值.
44.(2021·山东滨州市·八年级期末)(知识生成)
我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式,例如图1可以得到,基于此,请解答下列问题:
(1)根据图2,写出一个代数恒等式:_________.
(2)利用(1)中得到的结论,解决下面的问题:若,,则__________.
(3)小明同学用图3中张边长为的正方形,张边长为的正方形,张宽、长分别为、的长方形纸片拼出一个面积为长方形,则_________.
(知识迁移)
(4)事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图4表示的是一个边长为的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式:_________.
参考答案
1.D 2.B 3.B 4.D 5.D 6.C 7.D 8.B 9.C 10.B
11.B 12.B 13.A 14.D 15.C 16.D 17.B
18.36 6 19.250000 20. 21.1 22.29 23.1 24.8
25.0 26. 27. 28.80 29.64
30. 31.2 -5 5 32.-1 33.7 34.6
35.(1);(2)
【详解】
解:(1)
(2)
36.(1)10000;(2).
【详解】
解:(1)===10000.
(2)
=
=
=
=
=
=.
37.(1),;(2),
【详解】
解:(1)原式=,
把x=2,y=-1代入得:原式=;
(2)原式=,
把x=﹣2,y=代入得:原式=.
38.﹣7
【详解】
解:因为(a+b)2=25,(a﹣b)2=9,
所以(a﹣b)2﹣(a﹣b)2=4ab=16,
所以a2﹣6ab+b2=(a﹣b)2﹣4ab=9﹣16=﹣7.
39.5;47
【详解】
;
∵,
∴,即,
∴
40.(1);(2).
【详解】
解:(1)
(2)令,,
则,
由
∴
∴
即.
41.(1);(2),;,;,
【详解】
解:(1)列竖式如下:
(2)列竖式如下:
∵多项式能被二项式整除
∴余式
∵,均为自然数
∴,;,;,
42.(1)代数式有最小值为1;(2)代数式有最小值为3.(3)当,时,多项式有最大值为17.
【详解】
(1)原式
当时,代数式有最小值为1;
(2)原式
代数式有最小值为3.
(3)原式
当,时,多项式有最大值为17.
43.(1)m-n;(2)①(m-n)2;②(m+n)2-4mn;(3)(m-n)2=(m+n)2-4mn;(4),=±48;(5)3
【详解】
解:(1)由图可知,阴影部分小正方形的边长为:m-n;
(2)根据正方形的面积公式,阴影部分的面积为(m-n)2,
还可以表示为(m+n)2-4mn;
(3)根据阴影部分的面积相等,(m-n)2=(m+n)2-4mn;
(4)∵,
∴==36,
∴,
若,则===48,
若,则===-48;
(5)
=
=
∵,,
∴≥3,即最小值为3.
44.(1);(2)30;(3)16;(4).
【详解】
(1)由图2得:正方形的面积=(a+b+c)2;正方形的面积=a2+b2+c2+2ab+2ac+2bc,
∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,
故答案为:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
(2)∵(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,
∵a+b+c=10,ab+ac+bc=35,
∴102=a2+b2+c2+2×35,
∴a2+b2+c2=100-70=30,
故答案为:30;
(3)由题意得:(3a+b)(a+3b)=xa2+yb2+zab,
∴3a2+10ab+3b2=xa2+yb2+zab,
∴x=3,y=3,z=10,
∴x+y+z=16,
故答案为:16;
(4)∵原几何体的体积=x3-1×1?x=x3-x,新几何体的体积= x(x+1)(x-1),
∴x3-x= x(x+1)(x-1).
故答案为:x3-x=x(x+1)(x-1).
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
