2020--2021学年苏教版八年级数学下册《中心对称图形—平行四边形》能力提升单元检测卷(二)(word版含答案)
文档属性
| 名称 | 2020--2021学年苏教版八年级数学下册《中心对称图形—平行四边形》能力提升单元检测卷(二)(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 904.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 23:16:58 | ||
图片预览

文档简介
《中心对称图形—平行四边形》能力提升单元检测卷(二)
一、选择题
1.下列标志图中,既是轴对称图形,又是中心对称图形的是 ( )
2.下列说法正确的是 ( )
A.线段绕着它的中点旋转180°后与原线段重合,那么线段是中心对称图形
B.等边三角形绕着它的三边中线的交点旋转120°后与原图形重合,那么等边三角形是中心对称图形
C.正方形绕着它的对角线交点旋转90°后与原图形重合,那么正方形是中心对称图形
D.正五角星绕着它的中心旋转72°后与原图形重合,那么正五角星是中心对称图形
3.如图,在□ABCD中,AD=2AB,CE平分∠BCD交AD边于点E,且AE=3,则AB的长为 ( )
A.4 B.3 C. D.2
4.如图,在□ABCD中,对角线AC与BD相交于点O,过点O作EF⊥AC交BC于点E,交AD于点F,连接AE、CF,则四边形AECF是 ( )
A.梯形 B.矩形 C.菱形 D.正方形
5.如图,点E是矩形ABCD的边AD的延长线上一点,且AD=DE,连接
BE交CD于点O,连接AO,下列结论不正确的是 ( )
A.△AOB≌△BOC B.△BOC≌△EOD
C.△AOD≌△EOD D.△AOD≌△BOC
6.如图,在菱形ABCD中,∠BAD=120°.已知△ABC的周长是15,则菱形ABCD的周长是 ( )
A.25 B.20 C.15 D.10
7.如图,四边形ABCD四边的中点分别为E、F、G、H,对角线AC与BD相交于点O,若四边形EFGH的面积是3,则四边形ABCD的面积是 ( )
A.3 B.6 C.9 D.12
8. 将矩形纸片ABCD按如图所示的方式折叠,恰好得到菱形AECF.若AB=3,则菱形AECF的面积为( )
A.1; B.;C.;D.4;
二、填空题:
9.如图,在?ABCD中,BE平分∠ABC,BC=6,DE=2,则?ABCD的周长等于? .
10.如图,在矩形ABCD中,对角线AC,BD相交于点O,∠ACB=30°,则∠AOB的大小为 .
11.已知一个菱形的两条对角线长分别为6cm和8cm,则这个菱形的面积为? cm2.
12.如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点.若CD=5,则EF的长为 .
13.如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E.若∠CBF=20°,则∠AED等于? 度.
14.已知是正方形的对角线上一点,,过点作的垂线,交边于点,那么 = .
15.如图,在平行四边形中,是由绕顶点旋转40°所得,顶点恰好转到上一点的位置,则= 度.
第15题 第16题 第17题
16.如图,分别是正方形各边的中点,分别是四边形各边的中点,分别是的中点.若图中阴影部分的面积是10,则的长是 .
17.如图,菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则菱形的边长为
cm.
18.小明尝试着将矩形纸片 (如图(1) , )沿过点的直线折叠,使得点 落在边上的点处,折痕为 (如图(2));再沿过点的直线折叠,使得点落在边上的点处,点落在边上的点处,折痕为 (如图(3)).如果第二次折叠后,点正好在的平分线上,那么矩形长与宽的比值为 .
三、解答题
19.如图,在菱形ABCD中,M,N分别是边AB,BC的中点,MP⊥AB交边CD于点P,连接NM,NP.
(1)若∠B=60°,这时点P与点C重合,则∠NMP=__________度;
(2)求证:NM=NP;
(3)当△NPC为等腰三角形时,求∠B的度数.
20.如图,矩形ABCD中,点E,F分别在AB,CD边上,连接CE、AF,∠DCE=∠BAF.试判断四边形AECF的形状并加以证明.
21.如图,△ABC是等腰三角形,AB=BC,点D为BC的中点.
(1)用圆规和没有刻度的直尺作图,并保留作图痕迹:
①过点B作AC的平行线BP;
②过点D作BP的垂线,分别交AC,BP,BQ于点E,F,G.
(2)在(1)所作的图中,连接BE,CF.求证:四边形BFCE是平行四边形.
22.如图,中,是的角平分线,点为的中点,连接并延长到点,使,连接.
(1)求证:四边形是矩形;
(2)当满足什么条件时,矩形
是正方形,并说明理由.
23. (1)如图(1),在正方形中,点分别在边上,交于点,.求证: ;
(2)如图(2),在正方形中,点分别在边上,交于点,.求的长.
24.如图,在凸四边形中,为边的中点,且,分别过两点,作边的垂线,设两条垂线的交点为P.过点作于点.
求证: .
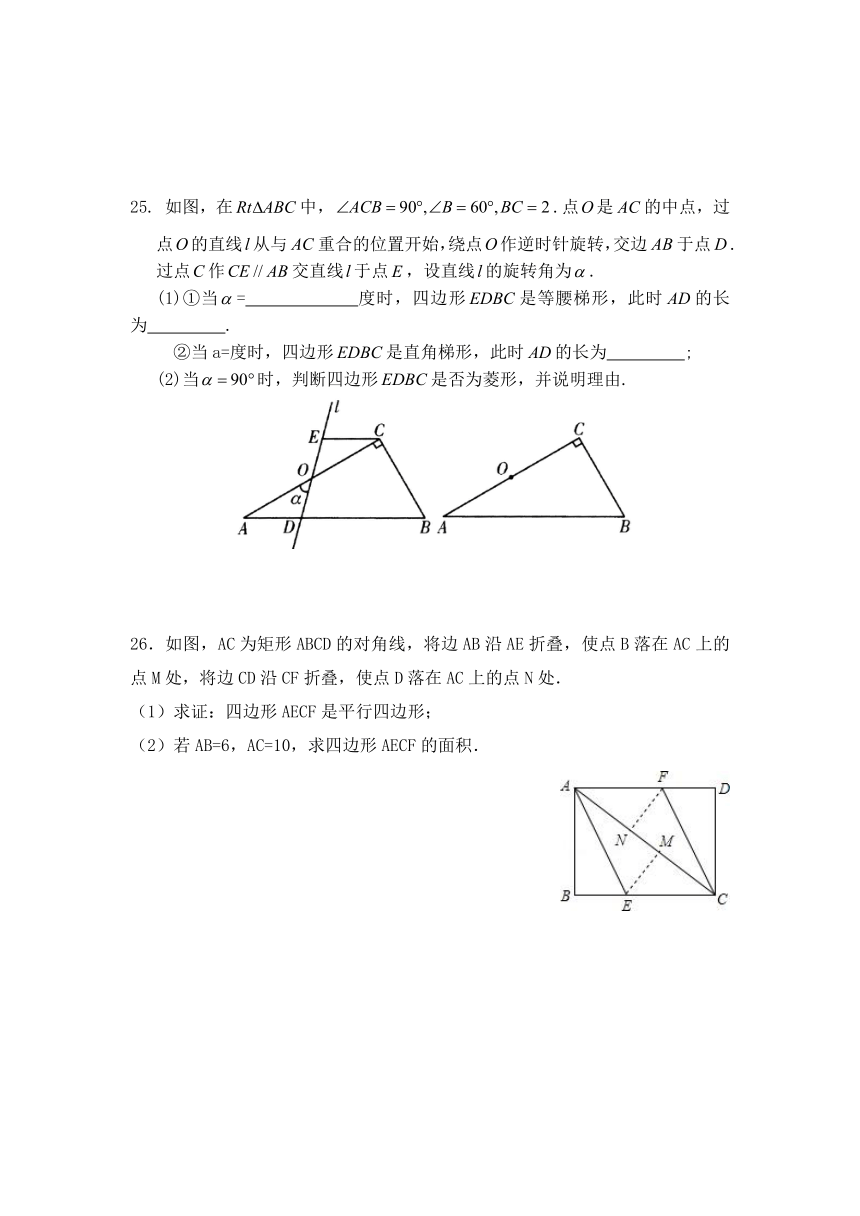
25. 如图,在中,.点是的中点,过点的直线从与重合的位置开始,绕点作逆时针旋转,交边于点.过点作交直线于点,设直线的旋转角为.
(1)①当= 度时,四边形是等腰梯形,此时的长为 .
②当a=度时,四边形是直角梯形,此时的长为 ;
(2)当时,判断四边形是否为菱形,并说明理由.
26.如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处.
(1)求证:四边形AECF是平行四边形;
(2)若AB=6,AC=10,求四边形AECF的面积.
参考答案
一、选择题
1.B 2.A 3.B 4.C 5.A 6.B 7.B 8.C;
二、填空题
11.20;12.60°;13.24;14.5;15.65;16.22.5°
17. 70 18. 8 19.13 20.
三、解答题
19.解:(1)∵MP⊥AB交边CD于点P,∠B=60°,点P与点C重合,
∴∠NPM=30°,∠BMP=90°,
∵N是BC的中点,∴MN=PN,
∴∠NMP=∠NPM=30°;
(2)
如图1,延长MN交DC的延长线于点E,
∵四边形ABCD是菱形,∴AB∥DC,
∴∠BMN=∠E,
∵点N是线段BC的中点,∴BN=CN,
在△MNB和△ENC中,
,
∴△MNB≌△ENC,
∴MN=EN,
即点N是线段ME的中点,
∵MP⊥AB交边CD于点P,
∴MP⊥DE,
∴∠MPE=90°,
∴PN=MN=ME;
(3)如图2
∵四边形ABCD是菱形,∴AB=BC,
又M,N分别是边AB,BC的中点,
∴MB=NB,
∴∠BMN=∠BNM,
由(2)知:△MNB≌△ENC,
∴∠BMN=∠BNM=∠E=∠CNE,
又∵PN=MN=NE,
∴∠NPE=∠E,
设∠BMN=∠BNM=∠E=∠CNE=∠NPE=x°,
则∠NCP=2x°,∠NPC=x°,
①若PN=PC,则∠PNC=∠NCP=2x°,
在△PNC中,2x+2x+x=180,
解得:x=36,
∴∠B=∠PNC+∠NPC=2x°+x°=36°×3=108°,
②若PC=NC,则∠PNC=∠NPC=x°,
在△PNC中,2x+x+x=180,
解得:x=45,
∴∠B=∠PNC+∠NPC=x°+x°=45°+45°=90°.
20.解:四边形AECF是平行四边形.
证明:∵矩形ABCD中,AB∥DC,
∴∠DCE=∠CEB,
∵∠DCE=∠BAF,
∴∠CEB=∠BAF,
∴FA∥CE,
又矩形ABCD中,
FC∥AE,
∴四边形AECF是平行四边形.
21.解:(1)如图:
(2)证明:如图:
∵BP∥AC,
∴∠ACB=∠PBC,
在△ECD和△FBD中,
,
∴△ECD≌△FBD,
∴CE=BF,
∴四边形ECFB是平行四边形.
22.(1)点为的中点,,
四边形是平行四边形.
是的角平分线,
四边形是矩形.
(2)当是等腰直角三角形,矩形是正方形.理由如下:
是等腰直角三角形,
由(1)知四边形是矩形,四边形是正方形.
23.(1)四边形为正方形,
≌
(2)过点作交于点,过点作交于点,与 交于点.
则四边形和四边形均为平行四边行.
.
故由(1)得,≌.
24. 如图,取、的中点分别是、;连接、、、;
易证:
≌.
四边形是平行四边形,
25.(1)①30,1 ②60,1.5
(2)当时,四边形是菱形.
,
四边形是平行四边形.
在中, ,
在中,
又四边形是平行四边形,
四边形是菱形.
26. (1)证明:∵折叠,
∴AM=AB,CN=CD,∠FNC=∠D=90°,∠AME=∠B=90°,
∴∠ANF=90°,∠CME=90°,
∵四边形ABCD为矩形,
∴AB=CD,AD∥BC,
∴AM=CN,
∴AM﹣MN=CN﹣MN,
即AN=CM,
在△ANF和△CME中,
,
∴△ANF≌△CME(ASA),
∴AF=CE,
又∵AF∥CE,
∴四边形AECF是平行四边形;
(2)解:∵AB=6,AC=10,∴BC=8,
设CE=x,则EM=8﹣x,CM=10﹣6=4,
在Rt△CEM中,
(8﹣x)2+42=x2,
解得:x=5,
∴四边形AECF的面积的面积为:EC?AB=5×6=30.
一、选择题
1.下列标志图中,既是轴对称图形,又是中心对称图形的是 ( )
2.下列说法正确的是 ( )
A.线段绕着它的中点旋转180°后与原线段重合,那么线段是中心对称图形
B.等边三角形绕着它的三边中线的交点旋转120°后与原图形重合,那么等边三角形是中心对称图形
C.正方形绕着它的对角线交点旋转90°后与原图形重合,那么正方形是中心对称图形
D.正五角星绕着它的中心旋转72°后与原图形重合,那么正五角星是中心对称图形
3.如图,在□ABCD中,AD=2AB,CE平分∠BCD交AD边于点E,且AE=3,则AB的长为 ( )
A.4 B.3 C. D.2
4.如图,在□ABCD中,对角线AC与BD相交于点O,过点O作EF⊥AC交BC于点E,交AD于点F,连接AE、CF,则四边形AECF是 ( )
A.梯形 B.矩形 C.菱形 D.正方形
5.如图,点E是矩形ABCD的边AD的延长线上一点,且AD=DE,连接
BE交CD于点O,连接AO,下列结论不正确的是 ( )
A.△AOB≌△BOC B.△BOC≌△EOD
C.△AOD≌△EOD D.△AOD≌△BOC
6.如图,在菱形ABCD中,∠BAD=120°.已知△ABC的周长是15,则菱形ABCD的周长是 ( )
A.25 B.20 C.15 D.10
7.如图,四边形ABCD四边的中点分别为E、F、G、H,对角线AC与BD相交于点O,若四边形EFGH的面积是3,则四边形ABCD的面积是 ( )
A.3 B.6 C.9 D.12
8. 将矩形纸片ABCD按如图所示的方式折叠,恰好得到菱形AECF.若AB=3,则菱形AECF的面积为( )
A.1; B.;C.;D.4;
二、填空题:
9.如图,在?ABCD中,BE平分∠ABC,BC=6,DE=2,则?ABCD的周长等于? .
10.如图,在矩形ABCD中,对角线AC,BD相交于点O,∠ACB=30°,则∠AOB的大小为 .
11.已知一个菱形的两条对角线长分别为6cm和8cm,则这个菱形的面积为? cm2.
12.如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点.若CD=5,则EF的长为 .
13.如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E.若∠CBF=20°,则∠AED等于? 度.
14.已知是正方形的对角线上一点,,过点作的垂线,交边于点,那么 = .
15.如图,在平行四边形中,是由绕顶点旋转40°所得,顶点恰好转到上一点的位置,则= 度.
第15题 第16题 第17题
16.如图,分别是正方形各边的中点,分别是四边形各边的中点,分别是的中点.若图中阴影部分的面积是10,则的长是 .
17.如图,菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则菱形的边长为
cm.
18.小明尝试着将矩形纸片 (如图(1) , )沿过点的直线折叠,使得点 落在边上的点处,折痕为 (如图(2));再沿过点的直线折叠,使得点落在边上的点处,点落在边上的点处,折痕为 (如图(3)).如果第二次折叠后,点正好在的平分线上,那么矩形长与宽的比值为 .
三、解答题
19.如图,在菱形ABCD中,M,N分别是边AB,BC的中点,MP⊥AB交边CD于点P,连接NM,NP.
(1)若∠B=60°,这时点P与点C重合,则∠NMP=__________度;
(2)求证:NM=NP;
(3)当△NPC为等腰三角形时,求∠B的度数.
20.如图,矩形ABCD中,点E,F分别在AB,CD边上,连接CE、AF,∠DCE=∠BAF.试判断四边形AECF的形状并加以证明.
21.如图,△ABC是等腰三角形,AB=BC,点D为BC的中点.
(1)用圆规和没有刻度的直尺作图,并保留作图痕迹:
①过点B作AC的平行线BP;
②过点D作BP的垂线,分别交AC,BP,BQ于点E,F,G.
(2)在(1)所作的图中,连接BE,CF.求证:四边形BFCE是平行四边形.
22.如图,中,是的角平分线,点为的中点,连接并延长到点,使,连接.
(1)求证:四边形是矩形;
(2)当满足什么条件时,矩形
是正方形,并说明理由.
23. (1)如图(1),在正方形中,点分别在边上,交于点,.求证: ;
(2)如图(2),在正方形中,点分别在边上,交于点,.求的长.
24.如图,在凸四边形中,为边的中点,且,分别过两点,作边的垂线,设两条垂线的交点为P.过点作于点.
求证: .
25. 如图,在中,.点是的中点,过点的直线从与重合的位置开始,绕点作逆时针旋转,交边于点.过点作交直线于点,设直线的旋转角为.
(1)①当= 度时,四边形是等腰梯形,此时的长为 .
②当a=度时,四边形是直角梯形,此时的长为 ;
(2)当时,判断四边形是否为菱形,并说明理由.
26.如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处.
(1)求证:四边形AECF是平行四边形;
(2)若AB=6,AC=10,求四边形AECF的面积.
参考答案
一、选择题
1.B 2.A 3.B 4.C 5.A 6.B 7.B 8.C;
二、填空题
11.20;12.60°;13.24;14.5;15.65;16.22.5°
17. 70 18. 8 19.13 20.
三、解答题
19.解:(1)∵MP⊥AB交边CD于点P,∠B=60°,点P与点C重合,
∴∠NPM=30°,∠BMP=90°,
∵N是BC的中点,∴MN=PN,
∴∠NMP=∠NPM=30°;
(2)
如图1,延长MN交DC的延长线于点E,
∵四边形ABCD是菱形,∴AB∥DC,
∴∠BMN=∠E,
∵点N是线段BC的中点,∴BN=CN,
在△MNB和△ENC中,
,
∴△MNB≌△ENC,
∴MN=EN,
即点N是线段ME的中点,
∵MP⊥AB交边CD于点P,
∴MP⊥DE,
∴∠MPE=90°,
∴PN=MN=ME;
(3)如图2
∵四边形ABCD是菱形,∴AB=BC,
又M,N分别是边AB,BC的中点,
∴MB=NB,
∴∠BMN=∠BNM,
由(2)知:△MNB≌△ENC,
∴∠BMN=∠BNM=∠E=∠CNE,
又∵PN=MN=NE,
∴∠NPE=∠E,
设∠BMN=∠BNM=∠E=∠CNE=∠NPE=x°,
则∠NCP=2x°,∠NPC=x°,
①若PN=PC,则∠PNC=∠NCP=2x°,
在△PNC中,2x+2x+x=180,
解得:x=36,
∴∠B=∠PNC+∠NPC=2x°+x°=36°×3=108°,
②若PC=NC,则∠PNC=∠NPC=x°,
在△PNC中,2x+x+x=180,
解得:x=45,
∴∠B=∠PNC+∠NPC=x°+x°=45°+45°=90°.
20.解:四边形AECF是平行四边形.
证明:∵矩形ABCD中,AB∥DC,
∴∠DCE=∠CEB,
∵∠DCE=∠BAF,
∴∠CEB=∠BAF,
∴FA∥CE,
又矩形ABCD中,
FC∥AE,
∴四边形AECF是平行四边形.
21.解:(1)如图:
(2)证明:如图:
∵BP∥AC,
∴∠ACB=∠PBC,
在△ECD和△FBD中,
,
∴△ECD≌△FBD,
∴CE=BF,
∴四边形ECFB是平行四边形.
22.(1)点为的中点,,
四边形是平行四边形.
是的角平分线,
四边形是矩形.
(2)当是等腰直角三角形,矩形是正方形.理由如下:
是等腰直角三角形,
由(1)知四边形是矩形,四边形是正方形.
23.(1)四边形为正方形,
≌
(2)过点作交于点,过点作交于点,与 交于点.
则四边形和四边形均为平行四边行.
.
故由(1)得,≌.
24. 如图,取、的中点分别是、;连接、、、;
易证:
≌.
四边形是平行四边形,
25.(1)①30,1 ②60,1.5
(2)当时,四边形是菱形.
,
四边形是平行四边形.
在中, ,
在中,
又四边形是平行四边形,
四边形是菱形.
26. (1)证明:∵折叠,
∴AM=AB,CN=CD,∠FNC=∠D=90°,∠AME=∠B=90°,
∴∠ANF=90°,∠CME=90°,
∵四边形ABCD为矩形,
∴AB=CD,AD∥BC,
∴AM=CN,
∴AM﹣MN=CN﹣MN,
即AN=CM,
在△ANF和△CME中,
,
∴△ANF≌△CME(ASA),
∴AF=CE,
又∵AF∥CE,
∴四边形AECF是平行四边形;
(2)解:∵AB=6,AC=10,∴BC=8,
设CE=x,则EM=8﹣x,CM=10﹣6=4,
在Rt△CEM中,
(8﹣x)2+42=x2,
解得:x=5,
∴四边形AECF的面积的面积为:EC?AB=5×6=30.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
