2020—2021学年人教版九年级数学下册第二十七章《相似》单元练习题(Word版 含答案)
文档属性
| 名称 | 2020—2021学年人教版九年级数学下册第二十七章《相似》单元练习题(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 762.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 00:00:00 | ||
图片预览




文档简介
人版教九年级数学下册第二十七章《相似》
单元练习题(含答案)
一、单选题
1.已知,点、、对应点分别是、、,,那么等于( )
A. B. C. D.
2.如图,已知和是以点为位似中心的位似图形,且和的周长之比为,点的坐标为,则点的坐标为( ).
A. B. C. D.
3.在与中,有下列条件:(1),(2);;,如果从中任取两个条件组成一组,那么能判断∽的共有
A.1组 B.2组 C.3组 D.4组
4.如图所示,在中,分别是的中点,分别交于点.下列命题中不正确的是( )
A. B.
C. D.
5.已知3x=4y,则的值为( )
A. B. C.7 D.
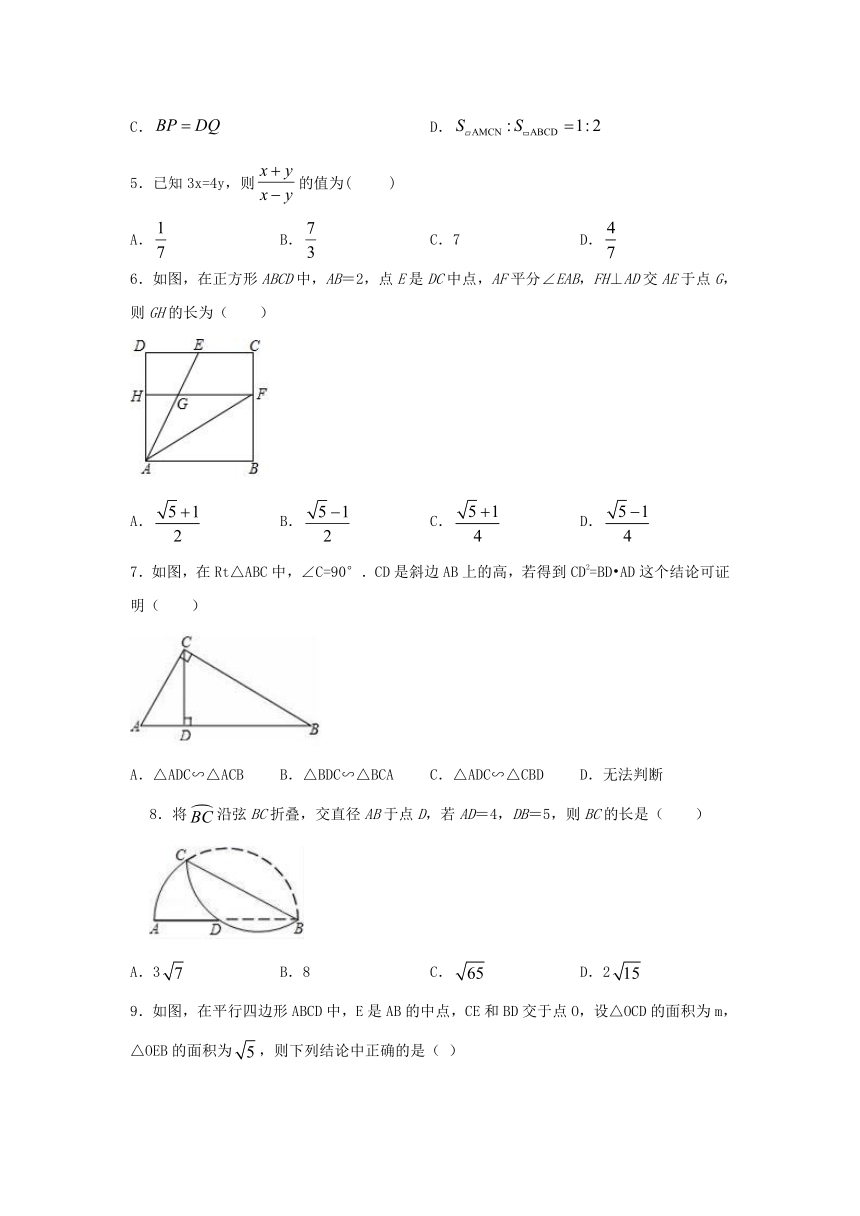
6.如图,在正方形ABCD中,AB=2,点E是DC中点,AF平分∠EAB,FH⊥AD交AE于点G,则GH的长为( )
A. B. C. D.
7.如图,在Rt△ABC中,∠C=90°.CD是斜边AB上的高,若得到CD2=BD?AD这个结论可证明( )
A.△ADC∽△ACB B.△BDC∽△BCA C.△ADC∽△CBD D.无法判断
8.将沿弦BC折叠,交直径AB于点D,若AD=4,DB=5,则BC的长是( )
A.3 B.8 C. D.2
9.如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,设△OCD的面积为m,△OEB的面积为,则下列结论中正确的是( )
A.m=5 B.m= C.m= D.m=10
10.已知四边形ABCD∽四边形A′B′C′D′,四边形ABCD与四边形A′B′C′D′的周长分别为24、36,则它们对角线AC与A′C′的比为(?? )
A.2:3 B.3:2 C.4:9 D.9:4
11.用一个5倍的放大镜去观察一个三角形,对此,四位同学有如下说法:
甲说:三角形的每个内角都扩大到原来的5倍;
乙说:三角形的每条边都扩大到原来的5倍;
丙说:三角形的面积扩大到原来的5倍;
丁说:三角形的周长都扩大到原来的5倍.上述说法中正确的是( )
A.甲和乙 B.乙和丙 C.丙和丁 D.乙和丁
12.已知△ABC,D是AC上一点,尺规在AB上确定一点E,使△ADE∽△ABC,则符合要求的作图痕迹是( )
A. B.
C. D.
二、填空题
13.如图,在△ABC中, E?F分别是AB和AC上的点,且EFBC,如果AB= 10,AE=6, AF=5,那么FC的长是______.
14.定义:我们知道,四边形的一条对角线把这个四边形分成两个三角形,如果这两个三角形相似但不全等,我们就把这条对角线叫做这个四边形的相似对角线,在四边形ABCD中,对角线BD是它的相似对角线,∠ABC=70°,BD平分∠ABC,那么∠ADC=____________度
15.如图,A是以EF为直径的半圆上的一点,作交EF于G,又B为AG上一点,EB的延长线交半圆于点K,若,,则______.
16.在太阳光下,如果一古塔在地面上留下的影长为50米,同时高1.5米的测竿的影长为2.5米,则古塔的高为 米.
17.如图,AB∥CD∥EF,如果AC=2,AE=6,DF=3,那么BD=_________.
18.如图,边长为4的正方形,是边上的中点,是直线上的动点,连接,将线段绕点逆时针旋转得到,连接,在点运动过程中,的最小值为______.
19.若两个相似三角形的面积比是,则这两个三角形的周长比为________;对应边上的中线的比为________.
20.如图,在?ABCD中,点E在边DC上,△DEF的面积与△BAF的面积之比为9:16,则EC:AB=_____.
三、解答题
21.如图,已知AB∥CD,AD,BC相交于E,F为EC上一点,且∠EAF=∠C.
求证:(1) ∠EAF=∠B; (2)AF2=FE·FB
22.如图,己知在△ABC中,AB=AC,tanB=,BC =4,点E是在线段BA延长线上一点,以点E为圆心,EC为半径的圆交射线BC于点C、F(点C、F不重合),射线EF与射线AC交于点P.
(1)求证:AE2=AP·AC;
(2)当点F在线段BC上,设CF=x,△PFC的面积为y,求y关于x的函数解析式及定义域;
(3)当 时,求BE的长.
23.已知内接于⊙O.
(1)当点O与AB有怎样的位置关系时,∠ACB是直角.
(2)在满足(1)的条件下,过点C作直线交AB于D,当CD与AB有什么样的关系时,△ABC∽△CBD∽△ACD.请画出符合(1)、(2)题意的两个图形后再作答.
24.如图,平行四边形ABCD的对角线AC、BD交于点O,点E在边CB的延长线上,且∠EAC=90°,AE2=EB?EC.
(1)求证:四边形ABCD是矩形;
(2)延长DB、AE交于点F,若AF=AC,求证:AE=BF.
25.如图,点F是中AC边的中点,,DF交AB于点E,交BC延长线于点G.
(1)若,,求BG的长;
(2)若,求证:.
26.如图,已知四边形ABCD是平行四边形,P为DC延长线上一点,AP分别交BD,BC于点M,N.
(1)证明:AM2=MN?MP;
(2)若AD=6,DC:CP=2:1,求BN的长.
27.如图,CD 为⊙O 的直径,弦 AB 交 CD 于点E,连接 BD、OB.
(1)求证:△AEC∽△DEB;
(2)若 CD⊥AB,AB=6,DE=1,求⊙O 的半径长.
28.如图,在中,,以为直径的交于点,交于点.过点作于点.
(1)求证:直线是的切线;
(2)若,,求
参考答案
1.B2.A3.C4.A5.C6.B7.C8.A9.B10.A11.D12.A
13.
14.145
15.
16.30.
17.1.5
18.
19.
20.
21.(1)∵AB∥CD,
∴∠B=∠C
又∵∠EAF=∠C,
∴∠EAF=∠B
(2)在△AFB与△EFA中,∵∠EAF=∠B,∠AFB=∠EFA,
∴△AFB∽△EFA
∴ ,即AF2=FE·FB
22.(1)∵∴
∵∴
∵
又∵
∴
∵是公共角,
∴
∴∴.
(2)∵
∴
∴.
过点作于点
∵经过圆心,
∴.∴.
在中,∵∴.
∴.
∴.
(3) ①当点F在线段BC上时,
∵
∴
∵△AEP∽△ACE.
∴
∴.
过点作垂足为点
∵ ∴
中,∵∴
∴∴.
②当点F在线段BC的延长线上时,
∵∠EFC=∠ECF, .
又∵∴
∴
∵是公共角,
∴ ,∴
∵∴
∴.
∴.
综上所述,或.
23.(1)点O在AB上时,∠ACB是直角;(2)CD与AB垂直相交于D时,△ABC∽△CBD∽△ACD.
24.(1)∵AE2=EB?EC
∴
又∵∠AEB=∠CEA
∴△AEB∽△CEA
∴∠EBA=∠EAC
而∠EAC=90°
∴∠EBA=∠EAC=90°
又∵∠EBA+∠CBA=180°
∴∠CBA=90°
而四边形ABCD是平行四边形
∴四边形ABCD是矩形
即得证.
(2)∵△AEB∽△CEA
∴即,∠EAB=∠ECA
∵四边形ABCD是矩形
∴OB=OC
∴∠OBC=∠ECA
∴∠EBF=∠OBC=∠ECA=∠EAB
即∠EBF=∠EAB
又∵∠F=∠F
∴△EBF∽△BAF
∴
∴
而AF=AC
∴BF=AE
即AE=BF得证.
25.(1)解:∵AD∥BC,
∴∠D=∠G,又∠AFD=∠CFG,AF=FC,
在△ADF和△CGF中
∴△ADF≌△CGF(AAS),
∴AD=CG,FG=FD,
又∵AD∥BC
∴△ADE∽△BGE
∴
又BE:AE=3:1,
∴BG=3AD,
又AD=CG
∴BC=2AD=8,
解得AD=4,
∴BG=3AD=12;
(2)证明:∵∠1=∠2,
∴180°-∠1=180°-∠2,
即∠AEF=∠FCG,
又∵∠AFE=∠GFC,
∴△AFE∽△GFC,
,
又AF=CF,DF=GF,
即,
∴FC2=FE?FD.
26.(1)在四边形ABCD是平行四边形中,
∵AD∥BC,
∴∠ADM=∠NBM,∠DAM=∠BNM,
∴△ADM∽△NBM,
∴,
∵AB∥DC,
∴∠P=∠BAM,∠MDP=∠ABM,
∴△PDM∽△ABM,
∴,
∴,
∴AM2=MN?MP;
(2)∵AD∥BC,
∴∠PCN=∠PDA,∠P=∠P,
∴△PCN∽△PDA,
∴,
∵DC:CP=2:1,
∴,
又∵AD=6,
∴NC=2,
∴BN=4.
27.(1)根据“同弧所对的圆周角相等”,
得∠A=∠D,∠C=∠ABD,
∴△AEC∽△DEB
(2)∵CD⊥AB,O为圆心,
∴BE=AB=3,
设⊙O的半径为r,
∵DE=1,则OE=r?1,
在Rt△OEB中,
由勾股定理得:OE2+EB2=OB2,
即:(r?1)2+32=r2,
解得r=5,即⊙O的半径为5.
28.(1)证明:连结,,
∵为直径,
∴,
∴,
∵,
∴,
∵,
∴是的中位线,
∴,
∵,
∴,
∴直线是的切线;
(2)解:连结,,
∵四边形内接于,
∴,
∵,
∴,
∵,
∴.
∴,
∵,,
∴,
∴,
∴,
∵为直径,
∴,
∴
单元练习题(含答案)
一、单选题
1.已知,点、、对应点分别是、、,,那么等于( )
A. B. C. D.
2.如图,已知和是以点为位似中心的位似图形,且和的周长之比为,点的坐标为,则点的坐标为( ).
A. B. C. D.
3.在与中,有下列条件:(1),(2);;,如果从中任取两个条件组成一组,那么能判断∽的共有
A.1组 B.2组 C.3组 D.4组
4.如图所示,在中,分别是的中点,分别交于点.下列命题中不正确的是( )
A. B.
C. D.
5.已知3x=4y,则的值为( )
A. B. C.7 D.
6.如图,在正方形ABCD中,AB=2,点E是DC中点,AF平分∠EAB,FH⊥AD交AE于点G,则GH的长为( )
A. B. C. D.
7.如图,在Rt△ABC中,∠C=90°.CD是斜边AB上的高,若得到CD2=BD?AD这个结论可证明( )
A.△ADC∽△ACB B.△BDC∽△BCA C.△ADC∽△CBD D.无法判断
8.将沿弦BC折叠,交直径AB于点D,若AD=4,DB=5,则BC的长是( )
A.3 B.8 C. D.2
9.如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,设△OCD的面积为m,△OEB的面积为,则下列结论中正确的是( )
A.m=5 B.m= C.m= D.m=10
10.已知四边形ABCD∽四边形A′B′C′D′,四边形ABCD与四边形A′B′C′D′的周长分别为24、36,则它们对角线AC与A′C′的比为(?? )
A.2:3 B.3:2 C.4:9 D.9:4
11.用一个5倍的放大镜去观察一个三角形,对此,四位同学有如下说法:
甲说:三角形的每个内角都扩大到原来的5倍;
乙说:三角形的每条边都扩大到原来的5倍;
丙说:三角形的面积扩大到原来的5倍;
丁说:三角形的周长都扩大到原来的5倍.上述说法中正确的是( )
A.甲和乙 B.乙和丙 C.丙和丁 D.乙和丁
12.已知△ABC,D是AC上一点,尺规在AB上确定一点E,使△ADE∽△ABC,则符合要求的作图痕迹是( )
A. B.
C. D.
二、填空题
13.如图,在△ABC中, E?F分别是AB和AC上的点,且EFBC,如果AB= 10,AE=6, AF=5,那么FC的长是______.
14.定义:我们知道,四边形的一条对角线把这个四边形分成两个三角形,如果这两个三角形相似但不全等,我们就把这条对角线叫做这个四边形的相似对角线,在四边形ABCD中,对角线BD是它的相似对角线,∠ABC=70°,BD平分∠ABC,那么∠ADC=____________度
15.如图,A是以EF为直径的半圆上的一点,作交EF于G,又B为AG上一点,EB的延长线交半圆于点K,若,,则______.
16.在太阳光下,如果一古塔在地面上留下的影长为50米,同时高1.5米的测竿的影长为2.5米,则古塔的高为 米.
17.如图,AB∥CD∥EF,如果AC=2,AE=6,DF=3,那么BD=_________.
18.如图,边长为4的正方形,是边上的中点,是直线上的动点,连接,将线段绕点逆时针旋转得到,连接,在点运动过程中,的最小值为______.
19.若两个相似三角形的面积比是,则这两个三角形的周长比为________;对应边上的中线的比为________.
20.如图,在?ABCD中,点E在边DC上,△DEF的面积与△BAF的面积之比为9:16,则EC:AB=_____.
三、解答题
21.如图,已知AB∥CD,AD,BC相交于E,F为EC上一点,且∠EAF=∠C.
求证:(1) ∠EAF=∠B; (2)AF2=FE·FB
22.如图,己知在△ABC中,AB=AC,tanB=,BC =4,点E是在线段BA延长线上一点,以点E为圆心,EC为半径的圆交射线BC于点C、F(点C、F不重合),射线EF与射线AC交于点P.
(1)求证:AE2=AP·AC;
(2)当点F在线段BC上,设CF=x,△PFC的面积为y,求y关于x的函数解析式及定义域;
(3)当 时,求BE的长.
23.已知内接于⊙O.
(1)当点O与AB有怎样的位置关系时,∠ACB是直角.
(2)在满足(1)的条件下,过点C作直线交AB于D,当CD与AB有什么样的关系时,△ABC∽△CBD∽△ACD.请画出符合(1)、(2)题意的两个图形后再作答.
24.如图,平行四边形ABCD的对角线AC、BD交于点O,点E在边CB的延长线上,且∠EAC=90°,AE2=EB?EC.
(1)求证:四边形ABCD是矩形;
(2)延长DB、AE交于点F,若AF=AC,求证:AE=BF.
25.如图,点F是中AC边的中点,,DF交AB于点E,交BC延长线于点G.
(1)若,,求BG的长;
(2)若,求证:.
26.如图,已知四边形ABCD是平行四边形,P为DC延长线上一点,AP分别交BD,BC于点M,N.
(1)证明:AM2=MN?MP;
(2)若AD=6,DC:CP=2:1,求BN的长.
27.如图,CD 为⊙O 的直径,弦 AB 交 CD 于点E,连接 BD、OB.
(1)求证:△AEC∽△DEB;
(2)若 CD⊥AB,AB=6,DE=1,求⊙O 的半径长.
28.如图,在中,,以为直径的交于点,交于点.过点作于点.
(1)求证:直线是的切线;
(2)若,,求
参考答案
1.B2.A3.C4.A5.C6.B7.C8.A9.B10.A11.D12.A
13.
14.145
15.
16.30.
17.1.5
18.
19.
20.
21.(1)∵AB∥CD,
∴∠B=∠C
又∵∠EAF=∠C,
∴∠EAF=∠B
(2)在△AFB与△EFA中,∵∠EAF=∠B,∠AFB=∠EFA,
∴△AFB∽△EFA
∴ ,即AF2=FE·FB
22.(1)∵∴
∵∴
∵
又∵
∴
∵是公共角,
∴
∴∴.
(2)∵
∴
∴.
过点作于点
∵经过圆心,
∴.∴.
在中,∵∴.
∴.
∴.
(3) ①当点F在线段BC上时,
∵
∴
∵△AEP∽△ACE.
∴
∴.
过点作垂足为点
∵ ∴
中,∵∴
∴∴.
②当点F在线段BC的延长线上时,
∵∠EFC=∠ECF, .
又∵∴
∴
∵是公共角,
∴ ,∴
∵∴
∴.
∴.
综上所述,或.
23.(1)点O在AB上时,∠ACB是直角;(2)CD与AB垂直相交于D时,△ABC∽△CBD∽△ACD.
24.(1)∵AE2=EB?EC
∴
又∵∠AEB=∠CEA
∴△AEB∽△CEA
∴∠EBA=∠EAC
而∠EAC=90°
∴∠EBA=∠EAC=90°
又∵∠EBA+∠CBA=180°
∴∠CBA=90°
而四边形ABCD是平行四边形
∴四边形ABCD是矩形
即得证.
(2)∵△AEB∽△CEA
∴即,∠EAB=∠ECA
∵四边形ABCD是矩形
∴OB=OC
∴∠OBC=∠ECA
∴∠EBF=∠OBC=∠ECA=∠EAB
即∠EBF=∠EAB
又∵∠F=∠F
∴△EBF∽△BAF
∴
∴
而AF=AC
∴BF=AE
即AE=BF得证.
25.(1)解:∵AD∥BC,
∴∠D=∠G,又∠AFD=∠CFG,AF=FC,
在△ADF和△CGF中
∴△ADF≌△CGF(AAS),
∴AD=CG,FG=FD,
又∵AD∥BC
∴△ADE∽△BGE
∴
又BE:AE=3:1,
∴BG=3AD,
又AD=CG
∴BC=2AD=8,
解得AD=4,
∴BG=3AD=12;
(2)证明:∵∠1=∠2,
∴180°-∠1=180°-∠2,
即∠AEF=∠FCG,
又∵∠AFE=∠GFC,
∴△AFE∽△GFC,
,
又AF=CF,DF=GF,
即,
∴FC2=FE?FD.
26.(1)在四边形ABCD是平行四边形中,
∵AD∥BC,
∴∠ADM=∠NBM,∠DAM=∠BNM,
∴△ADM∽△NBM,
∴,
∵AB∥DC,
∴∠P=∠BAM,∠MDP=∠ABM,
∴△PDM∽△ABM,
∴,
∴,
∴AM2=MN?MP;
(2)∵AD∥BC,
∴∠PCN=∠PDA,∠P=∠P,
∴△PCN∽△PDA,
∴,
∵DC:CP=2:1,
∴,
又∵AD=6,
∴NC=2,
∴BN=4.
27.(1)根据“同弧所对的圆周角相等”,
得∠A=∠D,∠C=∠ABD,
∴△AEC∽△DEB
(2)∵CD⊥AB,O为圆心,
∴BE=AB=3,
设⊙O的半径为r,
∵DE=1,则OE=r?1,
在Rt△OEB中,
由勾股定理得:OE2+EB2=OB2,
即:(r?1)2+32=r2,
解得r=5,即⊙O的半径为5.
28.(1)证明:连结,,
∵为直径,
∴,
∴,
∵,
∴,
∵,
∴是的中位线,
∴,
∵,
∴,
∴直线是的切线;
(2)解:连结,,
∵四边形内接于,
∴,
∵,
∴,
∵,
∴.
∴,
∵,,
∴,
∴,
∴,
∵为直径,
∴,
∴
