五年级数学下册教案-6.2 确定位置(二)(6) 北师大版
文档属性
| 名称 | 五年级数学下册教案-6.2 确定位置(二)(6) 北师大版 |

|
|
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-12 00:00:00 | ||
图片预览



文档简介
确定位置二教学设计
一、教学内容:
义务教育教科书北师大2011版小学数学五年级下册P67-P68.
二、教学目标
1.能描述和表示物体的位置。
2.通过解决实际问题,体会确定位置在生活中的实际应用,进一步了解确定物体位置的方法。
3.结合具体情境,能根据平面图确定图中任意两地的想对位置,以其中一地为观察点,度量另一地所在方向,以及两地的距离,感受数学与日常生活的密切联系。
三、教学重点:
根据平面图确定图中任意两地的想对位置
。
四、教学难点:
比较用数对与方向、距离确定位置的不同和相似之处。
五、教学准备:
作业纸、课件
六、课时安排:
1课时
七、教学过程:
1.回忆旧知,引出课题。
(1)同学们,我们学习了哪些确定位置的方法?
生1:在四年级学过用数对来确定位置。
生2:这个学期学习了用方向和距离来确定位置。
(2)在平面图中又该怎样确定位置呢?今天我们继续来研究确定位置。(板书课题确定位置二)
2.呈现问题,引导探究
(1)乐乐和同学们一起去大鸣山游玩,在爬山的过程中不小心迷路了,她想找到大本营的位置。
(2)请看,这是一张大鸣山风景区的平面图,借助这张平面图我们来帮助乐乐找到大本营的位置。
(3)仔细观察从图中你知道了哪些信息?
生1:我看见平面图中有一个方向板,知道这张地图是根据上北下南左西右东来规定方向的。
生2:1厘米表示100米,意思是地图上的1厘米表示实际生活中的100距离。
生3:我们可以看到乐乐现在在大鸣山。
(4)想一想,要准确的找到大本营的位置,必须要知道哪些要素?
(5)学生同桌交流。
生1:我们必须要找到观测点,这样才能确定大本营的方向。
生2:还要通过测量角度来精确大本营的方向。
生3:必须要知道从大鸣山到大本营的距离。
(6)画一画,大本营在大鸣山的什么位置?
学生动手操作。
(7)展示学生的画法。
生1:我把大本营和大鸣山两个地点用线连起来就知道大本营在大鸣山的东北方向。
生2:这样连起来只能知道大本营在大鸣山的东北方向,不能准确确定,我认为还要加上角度。
师:有道理,谁画得与他不同?
生3:我先在大鸣山画上方向板,再连接大本营和大鸣山,量出这个角是45°,在测量出这两点之间是5.6厘米,实际就是560米。
生4:我和刚才那位同学说得差不多,只是我量的是这个角。
(8)师:这两位同学都展示的正确。我们再通过课件演示刚才两位同学的画法。
(9)通过刚才两位同学的展示,我们发现方向、角度、距离对于确定大本营的位置都很重要。不过,只有一个大本营,怎么会有两个不同的角度。
生:一个角是从北向东的方向测量,另一个角是从东向北方向测量。
(10)师:对,大家在测量大本营方向时,选择的基准不同,一个是以北为基准,一个是以南为基准。一般情况下我们以指南针的方向为基准,即以北和南为基准。
2.实践应用,拓展延伸
(1)在大家热心的帮助下,乐乐顺利地回到了大本营。现在有三个小伙伴也在大本营附近。
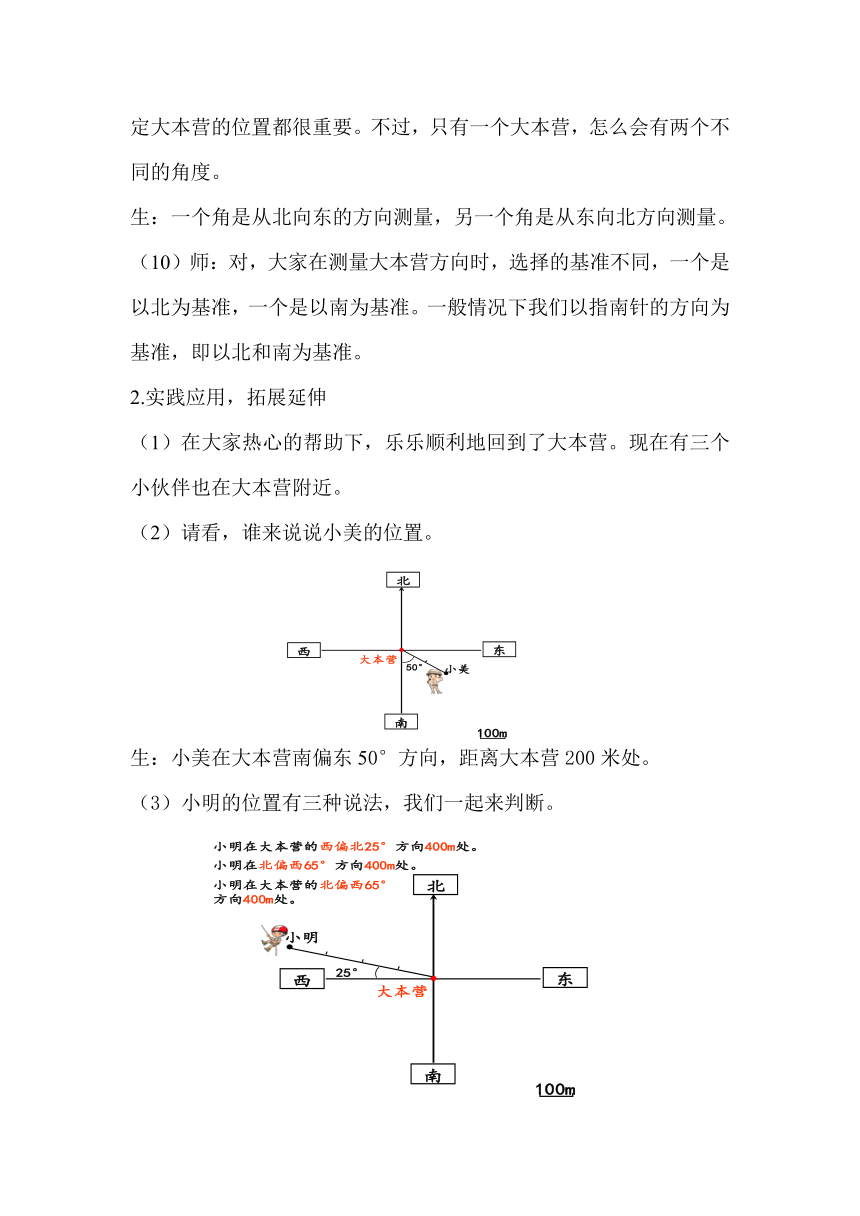
(2)请看,谁来说说小美的位置。
生:小美在大本营南偏东50°方向,距离大本营200米处。
(3)小明的位置有三种说法,我们一起来判断。
生1:从图中可以看出第一种说法是对的。
生2:第二种说法是错的,没有说观测点。
生3:北和西的夹角是90°,知道西偏北夹角是25°,就能算出北偏西夹角是65°,所以第三种说法是对的。
(4)现在给出丁丁位置的第一条信息,,能确定他的位置吗?猜一猜,丁丁可能在哪?
请一位学生上黑板指。
(5)看来,只告诉南偏西,我们只能确定这样的一个面。再给你一条信息,现在能确定丁丁的位置吗?
生:现在还不能确定丁丁的位置,因为我们还不知道距离。
师:如果说刚才丁丁的位置可能在一个面上,现在可能在哪?
生:应该在一条线上
(6)第三条信息给你,有了距离,能确定丁丁的位置吗?
生:现在可以确定丁丁的位置了,因为可以用一个点来表示丁丁的位置。
(7)回顾刚才的学习过程。如果只告诉你南偏西,只能确定一个什么?(面)加上角度,又能确定什么?(一条线)再加上距离,能确定一个什么?(点)
(8)在平面图中我们就是用这样一种由面到线再到点不断精确的方法来确定位置。
3.对比异同,沟通知识
(1)有一个数学迷同学想到了用数对的方法来确定大本营的位置。请看:
(2)从图中你知道什么?
生1:我知道大本营的位置是(4,4)
师:(4,4)表示什么意思?
生2:表示大本营在第四列,第四行。
生3:宝塔在(1,2),小清山在(4,1)。
师:大鸣山的位置该怎样表示?
生4:(0,0)。
(3)比较一下,这两种确定位置的方法,你觉得有什么不同?
生同桌讨论。
生1:数对是用列和行来表示位置的,而这个是用方向、角度、距离来确定位置的。
生2:在教室里我们可以用数对来确定位置很方便,我觉得数对一般用于小的范围。
生3:方向和距离可以在草原、大海航行时确定位置,这种方法适用于大的范围。
生4:在方向和距离这种方法里,能看出两地的距离,而在数对中却看不出来。
(4)同学们可真厉害!找出了它们之间的差别。再请大家深入思考,它们有没有相似的地方?
生同桌讨论。
生1:这两种方法都可以确定位置。
生2:它们都是用两个条件来确定位置的。
师:这两个条件能缺少一个吗?
生摆头,不能。
(5)以大本营为例,如果只给出大本营在大鸣山北偏东45°方向上,能确定大本营的位置吗?只能确定什么?
生:不能确定大本营的位置,只能确定它的位置是一条线。
(6)如果给出大本营距离大鸣山5.6千米呢?,它所在的位置可能在哪?就会是一个什么?
生:(生在课件上指,)有可能在每个方向,它的位置会是一个圆。
(10)现在同时给出方向和距离,能确定大本营的位置吗?
生:能,因为它们相较于一个点。
(11)再来看数对,如果只给你一个列数或行数,能确定位置吗?为什么?同时给呢?
生:只给行数,只知道大本营在这一行里,同样只给列数,只知道大本营在这一列里。同时给,它们相交于一点,就能确定位置了。
(12)瞧,看似两种不同的方法,但从根本上说都是用两个量确定平面上一个点的位置。其实,在平面上用两个不同的量确定位置的例子还有很多,在今后初中学习中,大家还将继续研究。
4.完成课堂练习。
八、板书设计
确定位置(二)
观测点——确定方向——确定距离
一、教学内容:
义务教育教科书北师大2011版小学数学五年级下册P67-P68.
二、教学目标
1.能描述和表示物体的位置。
2.通过解决实际问题,体会确定位置在生活中的实际应用,进一步了解确定物体位置的方法。
3.结合具体情境,能根据平面图确定图中任意两地的想对位置,以其中一地为观察点,度量另一地所在方向,以及两地的距离,感受数学与日常生活的密切联系。
三、教学重点:
根据平面图确定图中任意两地的想对位置
。
四、教学难点:
比较用数对与方向、距离确定位置的不同和相似之处。
五、教学准备:
作业纸、课件
六、课时安排:
1课时
七、教学过程:
1.回忆旧知,引出课题。
(1)同学们,我们学习了哪些确定位置的方法?
生1:在四年级学过用数对来确定位置。
生2:这个学期学习了用方向和距离来确定位置。
(2)在平面图中又该怎样确定位置呢?今天我们继续来研究确定位置。(板书课题确定位置二)
2.呈现问题,引导探究
(1)乐乐和同学们一起去大鸣山游玩,在爬山的过程中不小心迷路了,她想找到大本营的位置。
(2)请看,这是一张大鸣山风景区的平面图,借助这张平面图我们来帮助乐乐找到大本营的位置。
(3)仔细观察从图中你知道了哪些信息?
生1:我看见平面图中有一个方向板,知道这张地图是根据上北下南左西右东来规定方向的。
生2:1厘米表示100米,意思是地图上的1厘米表示实际生活中的100距离。
生3:我们可以看到乐乐现在在大鸣山。
(4)想一想,要准确的找到大本营的位置,必须要知道哪些要素?
(5)学生同桌交流。
生1:我们必须要找到观测点,这样才能确定大本营的方向。
生2:还要通过测量角度来精确大本营的方向。
生3:必须要知道从大鸣山到大本营的距离。
(6)画一画,大本营在大鸣山的什么位置?
学生动手操作。
(7)展示学生的画法。
生1:我把大本营和大鸣山两个地点用线连起来就知道大本营在大鸣山的东北方向。
生2:这样连起来只能知道大本营在大鸣山的东北方向,不能准确确定,我认为还要加上角度。
师:有道理,谁画得与他不同?
生3:我先在大鸣山画上方向板,再连接大本营和大鸣山,量出这个角是45°,在测量出这两点之间是5.6厘米,实际就是560米。
生4:我和刚才那位同学说得差不多,只是我量的是这个角。
(8)师:这两位同学都展示的正确。我们再通过课件演示刚才两位同学的画法。
(9)通过刚才两位同学的展示,我们发现方向、角度、距离对于确定大本营的位置都很重要。不过,只有一个大本营,怎么会有两个不同的角度。
生:一个角是从北向东的方向测量,另一个角是从东向北方向测量。
(10)师:对,大家在测量大本营方向时,选择的基准不同,一个是以北为基准,一个是以南为基准。一般情况下我们以指南针的方向为基准,即以北和南为基准。
2.实践应用,拓展延伸
(1)在大家热心的帮助下,乐乐顺利地回到了大本营。现在有三个小伙伴也在大本营附近。
(2)请看,谁来说说小美的位置。
生:小美在大本营南偏东50°方向,距离大本营200米处。
(3)小明的位置有三种说法,我们一起来判断。
生1:从图中可以看出第一种说法是对的。
生2:第二种说法是错的,没有说观测点。
生3:北和西的夹角是90°,知道西偏北夹角是25°,就能算出北偏西夹角是65°,所以第三种说法是对的。
(4)现在给出丁丁位置的第一条信息,,能确定他的位置吗?猜一猜,丁丁可能在哪?
请一位学生上黑板指。
(5)看来,只告诉南偏西,我们只能确定这样的一个面。再给你一条信息,现在能确定丁丁的位置吗?
生:现在还不能确定丁丁的位置,因为我们还不知道距离。
师:如果说刚才丁丁的位置可能在一个面上,现在可能在哪?
生:应该在一条线上
(6)第三条信息给你,有了距离,能确定丁丁的位置吗?
生:现在可以确定丁丁的位置了,因为可以用一个点来表示丁丁的位置。
(7)回顾刚才的学习过程。如果只告诉你南偏西,只能确定一个什么?(面)加上角度,又能确定什么?(一条线)再加上距离,能确定一个什么?(点)
(8)在平面图中我们就是用这样一种由面到线再到点不断精确的方法来确定位置。
3.对比异同,沟通知识
(1)有一个数学迷同学想到了用数对的方法来确定大本营的位置。请看:
(2)从图中你知道什么?
生1:我知道大本营的位置是(4,4)
师:(4,4)表示什么意思?
生2:表示大本营在第四列,第四行。
生3:宝塔在(1,2),小清山在(4,1)。
师:大鸣山的位置该怎样表示?
生4:(0,0)。
(3)比较一下,这两种确定位置的方法,你觉得有什么不同?
生同桌讨论。
生1:数对是用列和行来表示位置的,而这个是用方向、角度、距离来确定位置的。
生2:在教室里我们可以用数对来确定位置很方便,我觉得数对一般用于小的范围。
生3:方向和距离可以在草原、大海航行时确定位置,这种方法适用于大的范围。
生4:在方向和距离这种方法里,能看出两地的距离,而在数对中却看不出来。
(4)同学们可真厉害!找出了它们之间的差别。再请大家深入思考,它们有没有相似的地方?
生同桌讨论。
生1:这两种方法都可以确定位置。
生2:它们都是用两个条件来确定位置的。
师:这两个条件能缺少一个吗?
生摆头,不能。
(5)以大本营为例,如果只给出大本营在大鸣山北偏东45°方向上,能确定大本营的位置吗?只能确定什么?
生:不能确定大本营的位置,只能确定它的位置是一条线。
(6)如果给出大本营距离大鸣山5.6千米呢?,它所在的位置可能在哪?就会是一个什么?
生:(生在课件上指,)有可能在每个方向,它的位置会是一个圆。
(10)现在同时给出方向和距离,能确定大本营的位置吗?
生:能,因为它们相较于一个点。
(11)再来看数对,如果只给你一个列数或行数,能确定位置吗?为什么?同时给呢?
生:只给行数,只知道大本营在这一行里,同样只给列数,只知道大本营在这一列里。同时给,它们相交于一点,就能确定位置了。
(12)瞧,看似两种不同的方法,但从根本上说都是用两个量确定平面上一个点的位置。其实,在平面上用两个不同的量确定位置的例子还有很多,在今后初中学习中,大家还将继续研究。
4.完成课堂练习。
八、板书设计
确定位置(二)
观测点——确定方向——确定距离
