上海市吴淞中学2011-2012学年高二上学期期末考试数学试题
文档属性
| 名称 | 上海市吴淞中学2011-2012学年高二上学期期末考试数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 203.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-12 18:09:46 | ||
图片预览


文档简介
上海市吴淞中学2011-2012学年高二上学期期末考试数学试题
(满分150分,考试时间120分钟)
一.填空题(本大题满分56分)本大题共有14题,考生必须在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分。
1.若向量,,则等于 .5
2.正方体中,与直线异面,且与所成角为的面对角线共有 条.4
3.增广矩阵为的线性方程组的解为________________.
4.行列式中元素8的代数余子式为______________.=6
5.已知||=,||=,与的夹角为,则在上的投影为_____________.1
6.已知极限存在,则实数的取值范围是____________.
7.球的表面积为,则球的体积为___________.
8.已知是两个不共线的平面向量,向量,若,则=_____________.
9.已知数列中,,则数列的前项和= .
10.若取地球的半径为米,球面上两点位于东经,北纬,位于东经,北纬,则、两点的球面距离为_____________千米(结果精确到1千米).
11.已知正数数列()定义其“调和均数倒数”(),那么当时,=_______________.
12.如图,由编号,,…,,…(且)的圆柱自下而上组成.其中每一个圆柱的高与其底面圆的直径相等,且对于任意两个相邻圆柱,上面圆柱的高是下面圆柱的高的一半.若编号1的圆柱的高为,则所有圆柱的体积的和为_______________(结果保留).
13.若是等差数列,是互不相等的正整数,有正确的结论:
,类比上述性质,相应地,若等比数列,是互不相等的正整数,有_________.
14.如图1,一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点(图2).有下列四个命题:
A.正四棱锥的高等于正四棱柱高的一半;
B.将容器侧面水平放置时,水面也恰好过点;
C.任意摆放该容器,当水面静止时,水面都恰好经过点;
D.若往容器内再注入升水,则容器恰好能装满.
其中真命题的代号是:___________________(写出所有真命题的代号).B,D
二.选择题(本大题满分20分)本大题共有4题,每题有且只有一个正确答案。考生必须在答题纸的相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分。
15.用一个平面去截正方体,所得截面不可能是 ( D )
A.平面六边形 B.菱形 C.梯形 D.直角三角形
16.如图,为正方体的中心,△在该正方体各个面上的射影可能是( C )
A.(1)、(2)、(3)、(4) B.(1)、(3) C.(1)、(4) D.(2)、(4)
17.给出下列命题:(1)三点确定一个平面;(2)在空间中,过直线外一点只能作一条直线与该直线平行;(3)若平面上有不共线的三点到平面的距离相等,则;(4)若直线满足则.其中正确命题的个数是 ( B )
A. B. C. D.
18.点在所在平面内,给出下列关系式:
(1);
(2);
(3);
(4).
则点依次为的 ( C )
A.内心、外心、重心、垂心 B.重心、外心、内心、垂心
C.重心、垂心、内心、外心 D.外心、内心、垂心、重心
三.解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤。
19.(本题满分12分)
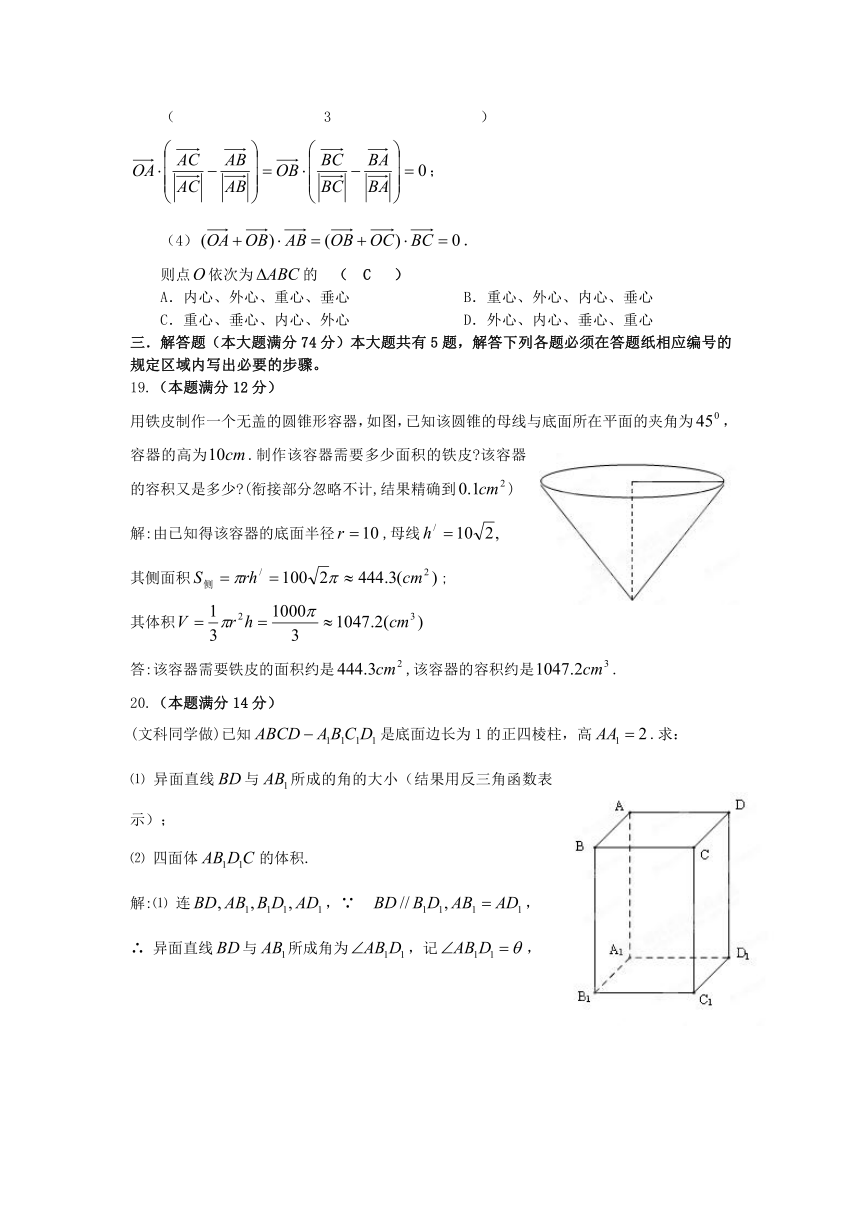
用铁皮制作一个无盖的圆锥形容器,如图,已知该圆锥的母线与底面所在平面的夹角为,容器的高为.制作该容器需要多少面积的铁皮 该容器的容积又是多少 (衔接部分忽略不计,结果精确到)
解:由已知得该容器的底面半径,母线
其侧面积;
其体积
答:该容器需要铁皮的面积约是,该容器的容积约是.
20.(本题满分14分)
(文科同学做)已知是底面边长为1的正四棱柱,高.求:
⑴ 异面直线与所成的角的大小(结果用反三角函数表示);
⑵ 四面体的体积.
解:⑴ 连,∵ ,
∴ 异面直线与所成角为,记,
∴ 异面直线与所成角为.
⑵ 连,则所求四面体的体积
.
20.(理科同学做)已知是底面边长为1的正四棱柱,是和的交点.
⑴设与底面所成的角的大小为,二面角的大小为,试确定与的一个等量关系,并给出证明;
⑵若点到平面的距离为,求正四棱柱的高.
解:设正四棱柱的高为.
⑴ 连,底面于,∴ 与底面所成的角为,即.
∵ ,为中点,∴,又,
∴ 是二面角的平面角,即.
∴ ,.
⑵ 建立如图空间直角坐标系,有
设平面的一个法向量为,
∵ ,取得
∴ 点到平面的距离为,则.
21.(本题满分14分)
已知向量,其中且,
(1)当为何值时,;
(2)解关于的不等式.
22.(本题满分16分)
如图,在四棱锥中,底面是矩形.已知.
(1)证明平面;
(2)求异面直线与所成的角的大小;
(3)求二面角的大小.
解:(1)证明:在中,由题设可得
于是.在矩形中,.又,
所以平面.
(2)解:由题设,,所以(或其补角)是异面直线与所成的角.
在中,由余弦定理得
由(1)知平面,平面,
所以,因而,于是是直角三角形,故.
所以异面直线与所成的角的大小为.
23.(本题满分18分)
各项均为正数的数列的前项和为,满足.
(1)求数列的通项公式;
(2)若数列满足,数列满足,数列的前项和为,求;
(3)若数列,甲同学利用第(2)问中的,试图确定的值是否可以等于2011?为此,他设计了一个程序(如图),但乙同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去,而无法结束),你是否同意乙同学的观点?请说明理由.
解:(1),
,,,
两式相减,得,,
为等差数列,首项为2,公差为1, .
(2)是首项为2,公比为2的等比数列,
乙同学的观点正确.
第12题
…
…
第14题
(满分150分,考试时间120分钟)
一.填空题(本大题满分56分)本大题共有14题,考生必须在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分。
1.若向量,,则等于 .5
2.正方体中,与直线异面,且与所成角为的面对角线共有 条.4
3.增广矩阵为的线性方程组的解为________________.
4.行列式中元素8的代数余子式为______________.=6
5.已知||=,||=,与的夹角为,则在上的投影为_____________.1
6.已知极限存在,则实数的取值范围是____________.
7.球的表面积为,则球的体积为___________.
8.已知是两个不共线的平面向量,向量,若,则=_____________.
9.已知数列中,,则数列的前项和= .
10.若取地球的半径为米,球面上两点位于东经,北纬,位于东经,北纬,则、两点的球面距离为_____________千米(结果精确到1千米).
11.已知正数数列()定义其“调和均数倒数”(),那么当时,=_______________.
12.如图,由编号,,…,,…(且)的圆柱自下而上组成.其中每一个圆柱的高与其底面圆的直径相等,且对于任意两个相邻圆柱,上面圆柱的高是下面圆柱的高的一半.若编号1的圆柱的高为,则所有圆柱的体积的和为_______________(结果保留).
13.若是等差数列,是互不相等的正整数,有正确的结论:
,类比上述性质,相应地,若等比数列,是互不相等的正整数,有_________.
14.如图1,一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点(图2).有下列四个命题:
A.正四棱锥的高等于正四棱柱高的一半;
B.将容器侧面水平放置时,水面也恰好过点;
C.任意摆放该容器,当水面静止时,水面都恰好经过点;
D.若往容器内再注入升水,则容器恰好能装满.
其中真命题的代号是:___________________(写出所有真命题的代号).B,D
二.选择题(本大题满分20分)本大题共有4题,每题有且只有一个正确答案。考生必须在答题纸的相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分。
15.用一个平面去截正方体,所得截面不可能是 ( D )
A.平面六边形 B.菱形 C.梯形 D.直角三角形
16.如图,为正方体的中心,△在该正方体各个面上的射影可能是( C )
A.(1)、(2)、(3)、(4) B.(1)、(3) C.(1)、(4) D.(2)、(4)
17.给出下列命题:(1)三点确定一个平面;(2)在空间中,过直线外一点只能作一条直线与该直线平行;(3)若平面上有不共线的三点到平面的距离相等,则;(4)若直线满足则.其中正确命题的个数是 ( B )
A. B. C. D.
18.点在所在平面内,给出下列关系式:
(1);
(2);
(3);
(4).
则点依次为的 ( C )
A.内心、外心、重心、垂心 B.重心、外心、内心、垂心
C.重心、垂心、内心、外心 D.外心、内心、垂心、重心
三.解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤。
19.(本题满分12分)
用铁皮制作一个无盖的圆锥形容器,如图,已知该圆锥的母线与底面所在平面的夹角为,容器的高为.制作该容器需要多少面积的铁皮 该容器的容积又是多少 (衔接部分忽略不计,结果精确到)
解:由已知得该容器的底面半径,母线
其侧面积;
其体积
答:该容器需要铁皮的面积约是,该容器的容积约是.
20.(本题满分14分)
(文科同学做)已知是底面边长为1的正四棱柱,高.求:
⑴ 异面直线与所成的角的大小(结果用反三角函数表示);
⑵ 四面体的体积.
解:⑴ 连,∵ ,
∴ 异面直线与所成角为,记,
∴ 异面直线与所成角为.
⑵ 连,则所求四面体的体积
.
20.(理科同学做)已知是底面边长为1的正四棱柱,是和的交点.
⑴设与底面所成的角的大小为,二面角的大小为,试确定与的一个等量关系,并给出证明;
⑵若点到平面的距离为,求正四棱柱的高.
解:设正四棱柱的高为.
⑴ 连,底面于,∴ 与底面所成的角为,即.
∵ ,为中点,∴,又,
∴ 是二面角的平面角,即.
∴ ,.
⑵ 建立如图空间直角坐标系,有
设平面的一个法向量为,
∵ ,取得
∴ 点到平面的距离为,则.
21.(本题满分14分)
已知向量,其中且,
(1)当为何值时,;
(2)解关于的不等式.
22.(本题满分16分)
如图,在四棱锥中,底面是矩形.已知.
(1)证明平面;
(2)求异面直线与所成的角的大小;
(3)求二面角的大小.
解:(1)证明:在中,由题设可得
于是.在矩形中,.又,
所以平面.
(2)解:由题设,,所以(或其补角)是异面直线与所成的角.
在中,由余弦定理得
由(1)知平面,平面,
所以,因而,于是是直角三角形,故.
所以异面直线与所成的角的大小为.
23.(本题满分18分)
各项均为正数的数列的前项和为,满足.
(1)求数列的通项公式;
(2)若数列满足,数列满足,数列的前项和为,求;
(3)若数列,甲同学利用第(2)问中的,试图确定的值是否可以等于2011?为此,他设计了一个程序(如图),但乙同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去,而无法结束),你是否同意乙同学的观点?请说明理由.
解:(1),
,,,
两式相减,得,,
为等差数列,首项为2,公差为1, .
(2)是首项为2,公比为2的等比数列,
乙同学的观点正确.
第12题
…
…
第14题
同课章节目录
