【21春课件】人教版四年级数学下册第5单元三角形[共5课时 108张PPT]
文档属性
| 名称 | 【21春课件】人教版四年级数学下册第5单元三角形[共5课时 108张PPT] |  | |
| 格式 | ppt | ||
| 文件大小 | 11.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-14 15:59:15 | ||
图片预览




文档简介
第1课时 三角形的特性
三角形
5
义务教育人教版四年级下册
情境导入
一
情境导入
一
1
画一个三角形。说一说三角形有几条边,几个角,几个顶点。
三角形有3条边。
探究新知
二
讨论:什么样的图形是三角形呢?
探究新知
二
顶点
顶点
顶点
角
角
角
边
边
边
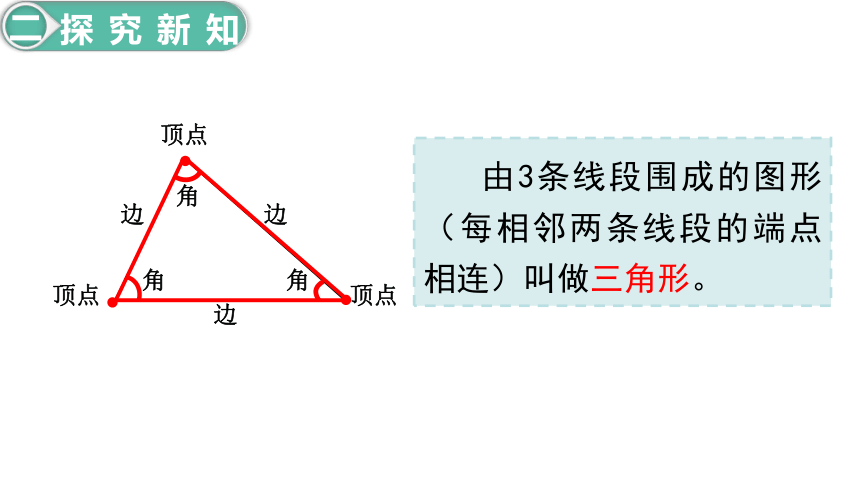
由3条线段围成的图形(每相邻两条线段的端点相连)叫做三角形。
探究新知
二
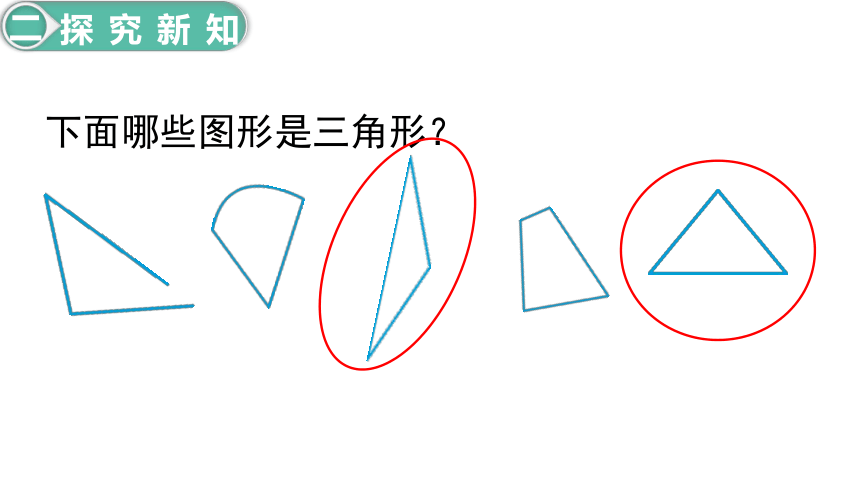
下面哪些图形是三角形?
探究新知
二
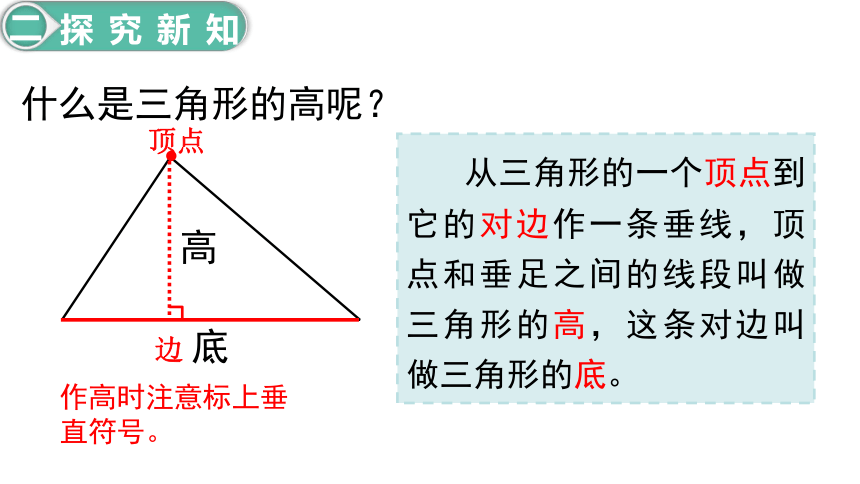
什么是三角形的高呢?
从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底。
高
底
顶点
边
作高时注意标上垂直符号。
探究新知
二
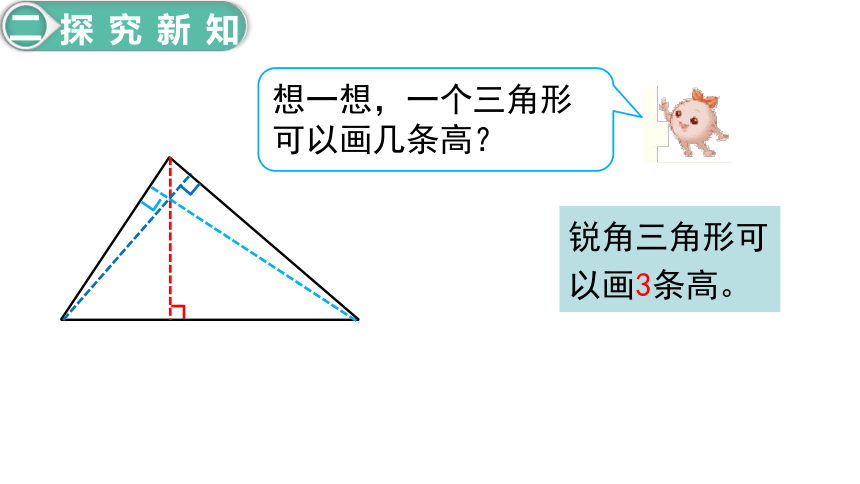
想一想,一个三角形可以画几条高?
锐角三角形可以画3条高。
探究新知
二
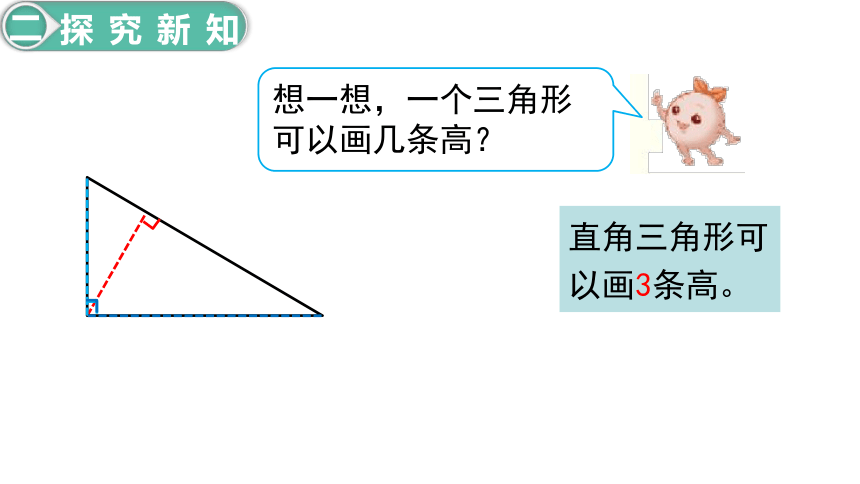
想一想,一个三角形可以画几条高?
直角三角形可以画3条高。
探究新知
二
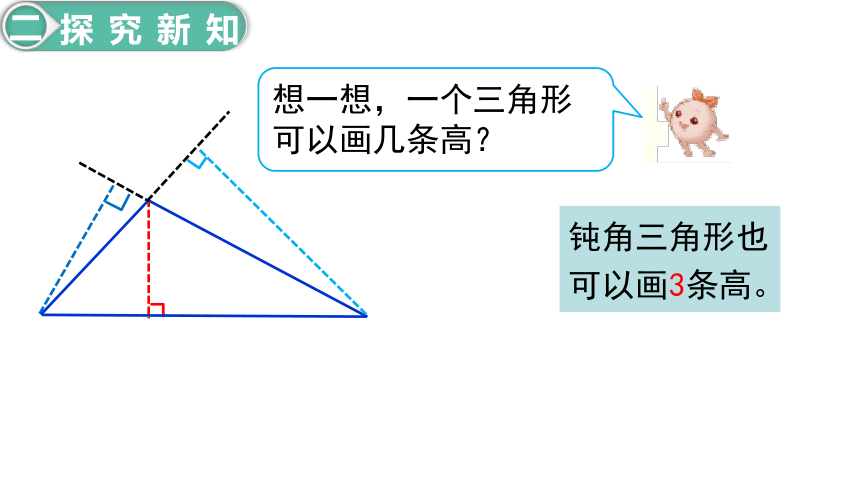
想一想,一个三角形可以画几条高?
钝角三角形也可以画3条高。
探究新知
二
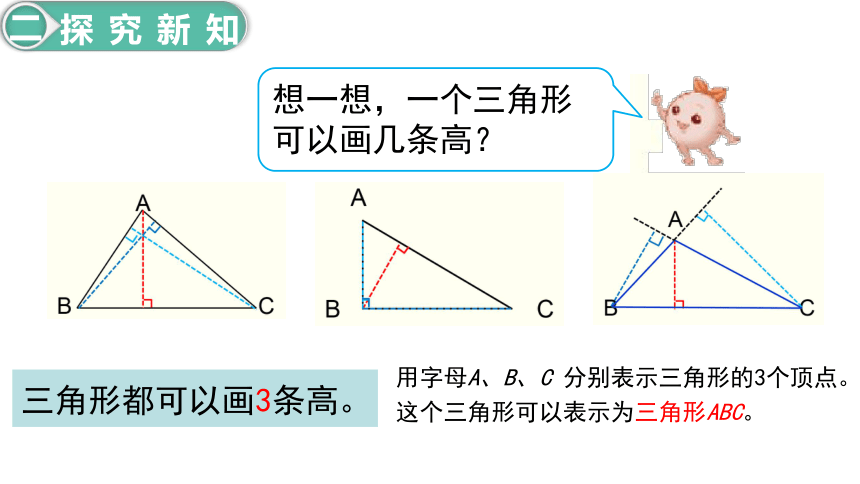
想一想,一个三角形可以画几条高?
三角形都可以画3条高。
用字母A、B、C 分别表示三角形的3个顶点。
这个三角形可以表示为三角形ABC。
探究新知
二
画出每个三角形指明的底边上的高。
底
底
底
探究新知
二
用3根小棒围三角形,用4根小棒围四边形,看看各能围出几个?(小棒的长度都一样)
2
探究新知
二
我围来围去,围出的都是一种三角形。
我已经围出3个形状不同的四边形了!
你发现了什么?
用3根小棒只能围出一种三角形,用4根小棒可以围出的四边形不唯一。
探究新知
二
看看下图中哪儿有三角形,想想它们有什么作用?
稳定、支撑
三角形具有稳定性
探究新知
二
举出生活中应用三角形稳定性的例子。
教材做一做
巩固练习
用3根木棒做成一个三角形,
用4根木棒做成一个长方形。
轻轻拉一拉。你发现了什么?
探究新知
二
我发现长方形很容易变形。
三角形不容易变形。
探究新知
二
1.画出每个三角形底边上的高。
底
底
底
教材P65T1
巩固练习
三
2.
教材P65T2
巩固练习
三
3.判断。
(1)由三条线段组成的图形是三角形。 ( )
(2)三角形有三条高,三条底。 ( )
(3)自行车车架运用了三角形的稳定性。( )
×
√
√
巩固练习
三
4. 盖房时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条。为什么要这样做呢?
四边形形状不稳定。斜钉一根木条后,就形成了两个三角形,利用三角形的稳定性可以预防窗框变形。
巩固练习
三
高
底
特征:3个顶点,3条边,3个角。
特性:三角形具有稳定性。
定义:由3条线段围成的图形(每相邻两条线段的端点相连)叫做三角形。
请同学们也画一个三角形,
并作出一条边上的高。
课堂小结
四
1.由3条线段( )的图形(每相邻两条线段的端点相连)叫做三角形。
2.一个三角形有( )个顶点,( )条边,( )个角,三角形具有( )性。
3.从三角形的( )到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的( )。
围成
3
3
3
稳定
顶点
高
课堂小结
四
第2课时 三角形三边的关系
三角形
5
义务教育人教版四年级下册
3
小明从家到学校有几条路线?
情境导入
一
3
共有3条路线。
探究新知
二
3
三条路线中哪条最短呢?
中间的路线最短。
为什么?
探究新知
二
3
最短
探究新知
二
两点间所有连线中线段最短,这条线段的长度叫做两点间的距离。
探究新知
二
我们来做个实验。
剪出下面4组纸条(单位:cm)。
(1)6、7、8。
(2)4、5、9。
(3)3、6、10。
(4)8、11、11。
用每组纸条摆三角形。
每组纸条都能摆出三角形吗?
4
想一想
探究新知
二
4
5
9
6
7
8
(1)
(2)
3
6
10
8
11
11
(3)
(4)
探究新知
二
4
5
9
(1)
(2)
6
7
8
√
3
6
10
8
11
11
(3)
(4)
探究新知
二
4
5
9
(1)
(2)
6
7
8
√
×
3
6
10
8
11
11
(3)
(4)
探究新知
二
4
5
9
(1)
(2)
6
7
8
√
×
3
6
10
8
11
11
(3)
(4)
×
探究新知
二
(1)
(2)
6
7
8
√
×
(3)
(4)
8
11
11
×
√
4
5
9
3
6
10
观察数据,你有什么发现?
探究新知
二
7
8
6
4
5
9
11
11
3
6
10
8
6+7>8 6+8>7 8+7>6
4+5=9 4+9>5 5+9>4
3+6<10 10+3>6 10+6>3
8+11>11 8+11>11 11+11>8
探究新知
二
7
8
6
4
5
9
11
11
3
6
10
8
6+7>8 6+8>7 8+7>6
4+5=9 4+9>5 5+9>4
3+6<10 10+3>6 10+6>3
8+11>11 8+11>11 11+11>8
三角形任意两边的和大于第三边。
探究新知
二
1.哪条路最近?
教材P66T6
巩固练习
三
2.在能拼成三角形的各组小棒下面画“√”(单位:cm)。
√
√
√
教材P66T7
巩固练习
三
3.判断下面哪三条线段可以组成一个三角形。
(单位:厘米)
(1)4 3 5 (2)2 6 7
(3)4 4 9 (4)3 9 8
√
√
√
巩固练习
三
4.一个三角形两条边是5厘米和10厘米,第三条边的长度(整厘米数)最短是多少厘米?最长是多少厘米?
三角形中,任意两边之和大于第三边,较短两边之和一定大于最长的边。
①第三条最短为:10-5+1=6(厘米)
②第三条最长为:10+5-1=14(厘米)
答:第三条边的长度最短是6厘米,最长是14厘米。
巩固练习
三
1.两点间所有连线中线段最短,这条线段的长度叫做两点间的距离。
2. 三角形三边的关系:三角形任意两边的和大于第三边。
3.判断三条线段能否围成三角形,只要把最短的两条边相加与最长边比较即可,如果最短的两边之和大于第三边,三条线段就能围成三角形。
课堂小结
四
第3课时 三角形的分类
三角形
5
义务教育人教版四年级下册
我们学过哪几种角?
锐角
直角
钝角
什么样的角是锐角?直角呢?钝角呢?
复习导入
一
今天我们就来学习三角形的分类。
三角形!
复习导入
一
5
给三角形分类。
有的三角形3个角都是锐角。
可以按照角来分。
有的三角形有一个钝角,两个……
探究新知
二
①3个角都是锐角的三角形是锐角三角形。
②有一个角是直角的三角形是直角三角形。
③有一个角是钝角的三角形是钝角三角形。
1.按角分类
探究新知
二
直角三角形
个直角, 个锐角
锐角三角形
个锐角
钝角三角形
个钝角, 个锐角
1
2
3
1
2
探究新知
二
锐角三角形
直角三角形
钝角三角形
把所有三角形作为一个整体,上面每种三角形作为这个整体的一部分,可以用图来表示它们之间的关系。
探究新知
二
三角形按角分类:锐角三角形
直角三角形
钝角三角形
探究新知
二
三角形按角分类:
锐角三角形
直角三角形
钝角三角形
探究新知
二
量一量:左边这个直角三角形的直角边和斜角边。
比一比:你发现了什么?
两条直角边的长度都小于斜边长度。
直角边
直角边
斜边
探究新知
二
除了按角分类,还有别的分法吗?
探究新知
二
观察一下,三角形的边有什么特点?
我发现有两条边相等的。
还有3条边都相等的。
探究新知
二
3条边都相等的三角形是等边三角形。
有2条边相等的三角形是等腰三角形。
2.按边分类
探究新知
二
顶角
腰
腰
底角
底角
底
等腰三角形
边
边
边
等边三角形
(也叫做正三角形)
分别量一量等腰三角形和等边三角形的各个角。
你发现了什么?
探究新知
二
等腰三角形
等边三角形
我发现等边三角形
也是等腰三角形。
等腰三角形两个底角相等。
等边三角形三个角都相等,
每个角都是60°。
探究新知
二
三条边相等
等边三角形
等腰三角形
两条边相等
三条边都不等
探究新知
二
三角形按边分类:
三角形
等腰三角形
等边三角形
探究新知
二
找一找,哪里有这两种特殊的三角形?
探究新知
二
教材做一做
巩固练习
三
1.(1)在钉子板上分别围出一个锐角三角形、直角三角形、钝角三角形和等腰三角形。
教材P65T4
巩固练习
三
(2)围出一个三角形,它既是锐角三角形又是等腰三角形。
教材P65T4
巩固练习
三
2.画出蚂蚁进洞的线路。
教材P65T5
巩固练习
三
我拿的三角形没有钝角。它可能是什么三角形?
可能是锐角三角形,还可能……
3. 猜一猜。
可能是锐角三角形和直角三角形。因为三角形按角分类时,只有这两类三角形没有钝角。
教材P66T9
巩固练习
三
4.一块等腰三角形的麦田,量得麦田的周长是208米,其中一条边长60米,求另外两边的长。
60米
60米
(1)若60米为腰,则另两边中的一条
边为腰,长度是60米,一条边为
底边,长:208-60×2=88(米),
60+60>88,符合题意。
巩固练习
三
4.一块等腰三角形的麦田,量得麦田的周长是208米,其中一条边长60米,求另外两边的长。
60米
(2)若60米为底边长,则另两边为腰,
腰长:(208-60)÷2=74(米),
60+74>74,符合题意
答:另外两边的长为60米、88米或74米、74米。
巩固练习
三
三角形
等腰三角形
等边三角形
三角形按边分类:
三角形按角分类:
锐角三角形
直角三角形
钝角三角形
课堂小结
四
第4课时 三角形的内角和
三角形
5
义务教育人教版四年级下册
360°
?
长方形的每个角是( )°,
它的内角和是( )°。
三角形的内角和是多少呢?
90
360
情境导入
一
60°
30°
90°
45°
90°
45°
每个三角尺的内角度数之和都180°。
60°+30°+90°=180°
45°+90°+45°=180°
探究新知
二
画几个不同类型的三角形。量一量,算一算,三角形3个内角的和各是多少度。
6
探究新知
二
65°
70°
45°
105°
25°
50°
三角形的形状
∠1
∠2
∠3
三个角的内角和
锐角三角形
70°
45°
65°
直角三角形
30°
90°
60°
钝角三角形
50°
25°
105°
通过测量,三角形的内角和都等于180°。
30°
90°
60°
180°
180°
180°
探究新知
二
先把一个三角形的三个角剪下来,再拼一拼。看一看,拼成了一个什么角。
1
2
3
拼成了一个平角。
探究新知
二
操作总会有误差,有没有别的办法说明呢?
探究新知
二
任意直角三角形的内角和是180 °。
360°
360°÷ 2=180°
操作总会有误差,有没有别的办法说明呢?
探究新知
二
把一个三角形分成两个三角形。
77°
探究新知
二
把一个三角形分成两个三角形。
77°
43°
探究新知
二
把一个三角形分成两个三角形。
77°
43°
60°
探究新知
二
把一个三角形分成两个三角形。
77°
43°
60°
77°+43°+60°=180°
探究新知
二
把一个三角形分成两个三角形。
77°
43°
60°
43°
60°
探究新知
二
把一个三角形分成两个三角形。
43°
60°
77°
43°
60°
47°
43°+90°+47°=180°
探究新知
二
把一个三角形分成两个三角形。
43°
60°
77°
43°
60°
47°
43°+90°+47°=180°
30°
90°+60°+30°=180°
探究新知
二
把一个三角形分成两个三角形。
43°
60°
77°
43°
60°
47°
30°
任意三角形的内角和是180 °。
探究新知
二
30°
60°
60°
30°
把两个三角形拼成一个大三角形,内角和是多少?
30°+ 30°+ 120°=180°
探究新知
二
1. 下面哪一组的三个角能组成三角形?
(1)30°、75°、80°。 ( )
×
(2)60°、60°、60°。 ( )
√
(3)110°、30°、45°。 ( )
×
(4)90°、15°、75°。 ( )
√
巩固练习
三
2. 在右图中,∠1=140°,∠3=25°。求∠2的度数。
∠1+∠2+∠3=180°
∠2=180°- ∠1- ∠3
=180°- 140°- 25°
=15°
答:∠2的度数是15°。
教材P67T1
巩固练习
三
3.算出下面各个未知角的度数。
180°- 65°- 37°=78°
90°- 30°=60°
180°- 25°- 20°=135°
教材P69T1
巩固练习
三
4.求出三角形各个角的度数。
(1)180°÷ 3=60°
三个角都是60°
教材P69T2
巩固练习
三
4.求出三角形各个角的度数。
(2)(180°-96°)÷ 2=42°
三个角分别是96°、42°、42°
教材P69T2
巩固练习
三
4.求出三角形各个角的度数。
(3)180°- 90°- 40°=50°
三个角分别是90°、40°、50°
教材P69T2
巩固练习
三
5.爸爸给小红买了一个等腰三角形的风筝。它的一个底角是70°,它的顶角是多少度?
180°-(70°× 2)=40°
答:它的顶角是40度。
70°
70°
教材P69T3
巩固练习
三
6.在一个等腰三角形中,一个顶角的度数是底角的4倍,这个三角形的顶角与底角各多少度?
1份
1份
4份
底角:180°÷(1+1+4)=30°
顶角:30°× 4=120°
答:这个三角形的顶角是120°,底角是30°。
巩固练习
三
第5课时 多边形的内角和
三角形
5
义务教育人教版四年级下册
连一连。
长方形
正方形
平行四边形
梯形
这些图形的内角和是多少呢?
复习导入
一
四边形的内角和是多少度?
四边形可以分成几种图形
长方形
正方形
平行四边形
梯形
普通四边形
这些图形的内角和是不是一样的呢?
7
阅读与理解
探究新知
二
90?×4=360°
长方形和正方形的4个角都是直角,它们的内角和是360°。
分析与操作
探究新知
二
方法一:测量法
70°+60°+120°+110°=360°
70°
60°
120°
110°
你能想到什么办法求出其他四边形的内角和呢?
探究新知
二
1
1
2
2
4
3
3
4
我把这个四边形的4个角剪下来拼成了一个周角。
方法二:拼图法
探究新知
二
我把这个四边形分成了2个三角形。
一个三角形的内角和是180°,两个相加为360°。
四边形的内角和是_____。
360°
方法三:转化法
探究新知
二
我们大家共同证明了所有四边形的内角和都是360°。
回顾与反思
探究新知
二
你能想办法求出右边这个多边形的内角和吗?
你是怎么想的呢?
提示:将五边形分成三角形再计算!
教材做一做
巩固练习
三
我把这个五边形分成了三个三角形,180?×3=540?。
我把这个五边形分成了5个三角形,把5个三角形的内角加起来再减去中间的一个周角,180?×5-360?=540?。
巩固练习
三
六边形、七边形……的内角和是多少呢?
巩固练习
三
1.画一画,算一算,你发现了什么?
6
7
2
3
180?×4
180?×5
发现:每个多边形都可以分成(边数-2)个三角形,多边形的
内角和=180?×(边数-2)。
教材P69T4
巩固练习
三
2.*下面图形中各有多少个三角形?有什么规律?
1
1+2=3
1+2+3=6
1+2+3+4=10
第n幅图三角形个数为1+2+3+…+(n-1)+n,n为大三角形被分成的三角形个数。
教材P70T7
巩固练习
三
三角形
5
义务教育人教版四年级下册
情境导入
一
情境导入
一
1
画一个三角形。说一说三角形有几条边,几个角,几个顶点。
三角形有3条边。
探究新知
二
讨论:什么样的图形是三角形呢?
探究新知
二
顶点
顶点
顶点
角
角
角
边
边
边
由3条线段围成的图形(每相邻两条线段的端点相连)叫做三角形。
探究新知
二
下面哪些图形是三角形?
探究新知
二
什么是三角形的高呢?
从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底。
高
底
顶点
边
作高时注意标上垂直符号。
探究新知
二
想一想,一个三角形可以画几条高?
锐角三角形可以画3条高。
探究新知
二
想一想,一个三角形可以画几条高?
直角三角形可以画3条高。
探究新知
二
想一想,一个三角形可以画几条高?
钝角三角形也可以画3条高。
探究新知
二
想一想,一个三角形可以画几条高?
三角形都可以画3条高。
用字母A、B、C 分别表示三角形的3个顶点。
这个三角形可以表示为三角形ABC。
探究新知
二
画出每个三角形指明的底边上的高。
底
底
底
探究新知
二
用3根小棒围三角形,用4根小棒围四边形,看看各能围出几个?(小棒的长度都一样)
2
探究新知
二
我围来围去,围出的都是一种三角形。
我已经围出3个形状不同的四边形了!
你发现了什么?
用3根小棒只能围出一种三角形,用4根小棒可以围出的四边形不唯一。
探究新知
二
看看下图中哪儿有三角形,想想它们有什么作用?
稳定、支撑
三角形具有稳定性
探究新知
二
举出生活中应用三角形稳定性的例子。
教材做一做
巩固练习
用3根木棒做成一个三角形,
用4根木棒做成一个长方形。
轻轻拉一拉。你发现了什么?
探究新知
二
我发现长方形很容易变形。
三角形不容易变形。
探究新知
二
1.画出每个三角形底边上的高。
底
底
底
教材P65T1
巩固练习
三
2.
教材P65T2
巩固练习
三
3.判断。
(1)由三条线段组成的图形是三角形。 ( )
(2)三角形有三条高,三条底。 ( )
(3)自行车车架运用了三角形的稳定性。( )
×
√
√
巩固练习
三
4. 盖房时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条。为什么要这样做呢?
四边形形状不稳定。斜钉一根木条后,就形成了两个三角形,利用三角形的稳定性可以预防窗框变形。
巩固练习
三
高
底
特征:3个顶点,3条边,3个角。
特性:三角形具有稳定性。
定义:由3条线段围成的图形(每相邻两条线段的端点相连)叫做三角形。
请同学们也画一个三角形,
并作出一条边上的高。
课堂小结
四
1.由3条线段( )的图形(每相邻两条线段的端点相连)叫做三角形。
2.一个三角形有( )个顶点,( )条边,( )个角,三角形具有( )性。
3.从三角形的( )到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的( )。
围成
3
3
3
稳定
顶点
高
课堂小结
四
第2课时 三角形三边的关系
三角形
5
义务教育人教版四年级下册
3
小明从家到学校有几条路线?
情境导入
一
3
共有3条路线。
探究新知
二
3
三条路线中哪条最短呢?
中间的路线最短。
为什么?
探究新知
二
3
最短
探究新知
二
两点间所有连线中线段最短,这条线段的长度叫做两点间的距离。
探究新知
二
我们来做个实验。
剪出下面4组纸条(单位:cm)。
(1)6、7、8。
(2)4、5、9。
(3)3、6、10。
(4)8、11、11。
用每组纸条摆三角形。
每组纸条都能摆出三角形吗?
4
想一想
探究新知
二
4
5
9
6
7
8
(1)
(2)
3
6
10
8
11
11
(3)
(4)
探究新知
二
4
5
9
(1)
(2)
6
7
8
√
3
6
10
8
11
11
(3)
(4)
探究新知
二
4
5
9
(1)
(2)
6
7
8
√
×
3
6
10
8
11
11
(3)
(4)
探究新知
二
4
5
9
(1)
(2)
6
7
8
√
×
3
6
10
8
11
11
(3)
(4)
×
探究新知
二
(1)
(2)
6
7
8
√
×
(3)
(4)
8
11
11
×
√
4
5
9
3
6
10
观察数据,你有什么发现?
探究新知
二
7
8
6
4
5
9
11
11
3
6
10
8
6+7>8 6+8>7 8+7>6
4+5=9 4+9>5 5+9>4
3+6<10 10+3>6 10+6>3
8+11>11 8+11>11 11+11>8
探究新知
二
7
8
6
4
5
9
11
11
3
6
10
8
6+7>8 6+8>7 8+7>6
4+5=9 4+9>5 5+9>4
3+6<10 10+3>6 10+6>3
8+11>11 8+11>11 11+11>8
三角形任意两边的和大于第三边。
探究新知
二
1.哪条路最近?
教材P66T6
巩固练习
三
2.在能拼成三角形的各组小棒下面画“√”(单位:cm)。
√
√
√
教材P66T7
巩固练习
三
3.判断下面哪三条线段可以组成一个三角形。
(单位:厘米)
(1)4 3 5 (2)2 6 7
(3)4 4 9 (4)3 9 8
√
√
√
巩固练习
三
4.一个三角形两条边是5厘米和10厘米,第三条边的长度(整厘米数)最短是多少厘米?最长是多少厘米?
三角形中,任意两边之和大于第三边,较短两边之和一定大于最长的边。
①第三条最短为:10-5+1=6(厘米)
②第三条最长为:10+5-1=14(厘米)
答:第三条边的长度最短是6厘米,最长是14厘米。
巩固练习
三
1.两点间所有连线中线段最短,这条线段的长度叫做两点间的距离。
2. 三角形三边的关系:三角形任意两边的和大于第三边。
3.判断三条线段能否围成三角形,只要把最短的两条边相加与最长边比较即可,如果最短的两边之和大于第三边,三条线段就能围成三角形。
课堂小结
四
第3课时 三角形的分类
三角形
5
义务教育人教版四年级下册
我们学过哪几种角?
锐角
直角
钝角
什么样的角是锐角?直角呢?钝角呢?
复习导入
一
今天我们就来学习三角形的分类。
三角形!
复习导入
一
5
给三角形分类。
有的三角形3个角都是锐角。
可以按照角来分。
有的三角形有一个钝角,两个……
探究新知
二
①3个角都是锐角的三角形是锐角三角形。
②有一个角是直角的三角形是直角三角形。
③有一个角是钝角的三角形是钝角三角形。
1.按角分类
探究新知
二
直角三角形
个直角, 个锐角
锐角三角形
个锐角
钝角三角形
个钝角, 个锐角
1
2
3
1
2
探究新知
二
锐角三角形
直角三角形
钝角三角形
把所有三角形作为一个整体,上面每种三角形作为这个整体的一部分,可以用图来表示它们之间的关系。
探究新知
二
三角形按角分类:锐角三角形
直角三角形
钝角三角形
探究新知
二
三角形按角分类:
锐角三角形
直角三角形
钝角三角形
探究新知
二
量一量:左边这个直角三角形的直角边和斜角边。
比一比:你发现了什么?
两条直角边的长度都小于斜边长度。
直角边
直角边
斜边
探究新知
二
除了按角分类,还有别的分法吗?
探究新知
二
观察一下,三角形的边有什么特点?
我发现有两条边相等的。
还有3条边都相等的。
探究新知
二
3条边都相等的三角形是等边三角形。
有2条边相等的三角形是等腰三角形。
2.按边分类
探究新知
二
顶角
腰
腰
底角
底角
底
等腰三角形
边
边
边
等边三角形
(也叫做正三角形)
分别量一量等腰三角形和等边三角形的各个角。
你发现了什么?
探究新知
二
等腰三角形
等边三角形
我发现等边三角形
也是等腰三角形。
等腰三角形两个底角相等。
等边三角形三个角都相等,
每个角都是60°。
探究新知
二
三条边相等
等边三角形
等腰三角形
两条边相等
三条边都不等
探究新知
二
三角形按边分类:
三角形
等腰三角形
等边三角形
探究新知
二
找一找,哪里有这两种特殊的三角形?
探究新知
二
教材做一做
巩固练习
三
1.(1)在钉子板上分别围出一个锐角三角形、直角三角形、钝角三角形和等腰三角形。
教材P65T4
巩固练习
三
(2)围出一个三角形,它既是锐角三角形又是等腰三角形。
教材P65T4
巩固练习
三
2.画出蚂蚁进洞的线路。
教材P65T5
巩固练习
三
我拿的三角形没有钝角。它可能是什么三角形?
可能是锐角三角形,还可能……
3. 猜一猜。
可能是锐角三角形和直角三角形。因为三角形按角分类时,只有这两类三角形没有钝角。
教材P66T9
巩固练习
三
4.一块等腰三角形的麦田,量得麦田的周长是208米,其中一条边长60米,求另外两边的长。
60米
60米
(1)若60米为腰,则另两边中的一条
边为腰,长度是60米,一条边为
底边,长:208-60×2=88(米),
60+60>88,符合题意。
巩固练习
三
4.一块等腰三角形的麦田,量得麦田的周长是208米,其中一条边长60米,求另外两边的长。
60米
(2)若60米为底边长,则另两边为腰,
腰长:(208-60)÷2=74(米),
60+74>74,符合题意
答:另外两边的长为60米、88米或74米、74米。
巩固练习
三
三角形
等腰三角形
等边三角形
三角形按边分类:
三角形按角分类:
锐角三角形
直角三角形
钝角三角形
课堂小结
四
第4课时 三角形的内角和
三角形
5
义务教育人教版四年级下册
360°
?
长方形的每个角是( )°,
它的内角和是( )°。
三角形的内角和是多少呢?
90
360
情境导入
一
60°
30°
90°
45°
90°
45°
每个三角尺的内角度数之和都180°。
60°+30°+90°=180°
45°+90°+45°=180°
探究新知
二
画几个不同类型的三角形。量一量,算一算,三角形3个内角的和各是多少度。
6
探究新知
二
65°
70°
45°
105°
25°
50°
三角形的形状
∠1
∠2
∠3
三个角的内角和
锐角三角形
70°
45°
65°
直角三角形
30°
90°
60°
钝角三角形
50°
25°
105°
通过测量,三角形的内角和都等于180°。
30°
90°
60°
180°
180°
180°
探究新知
二
先把一个三角形的三个角剪下来,再拼一拼。看一看,拼成了一个什么角。
1
2
3
拼成了一个平角。
探究新知
二
操作总会有误差,有没有别的办法说明呢?
探究新知
二
任意直角三角形的内角和是180 °。
360°
360°÷ 2=180°
操作总会有误差,有没有别的办法说明呢?
探究新知
二
把一个三角形分成两个三角形。
77°
探究新知
二
把一个三角形分成两个三角形。
77°
43°
探究新知
二
把一个三角形分成两个三角形。
77°
43°
60°
探究新知
二
把一个三角形分成两个三角形。
77°
43°
60°
77°+43°+60°=180°
探究新知
二
把一个三角形分成两个三角形。
77°
43°
60°
43°
60°
探究新知
二
把一个三角形分成两个三角形。
43°
60°
77°
43°
60°
47°
43°+90°+47°=180°
探究新知
二
把一个三角形分成两个三角形。
43°
60°
77°
43°
60°
47°
43°+90°+47°=180°
30°
90°+60°+30°=180°
探究新知
二
把一个三角形分成两个三角形。
43°
60°
77°
43°
60°
47°
30°
任意三角形的内角和是180 °。
探究新知
二
30°
60°
60°
30°
把两个三角形拼成一个大三角形,内角和是多少?
30°+ 30°+ 120°=180°
探究新知
二
1. 下面哪一组的三个角能组成三角形?
(1)30°、75°、80°。 ( )
×
(2)60°、60°、60°。 ( )
√
(3)110°、30°、45°。 ( )
×
(4)90°、15°、75°。 ( )
√
巩固练习
三
2. 在右图中,∠1=140°,∠3=25°。求∠2的度数。
∠1+∠2+∠3=180°
∠2=180°- ∠1- ∠3
=180°- 140°- 25°
=15°
答:∠2的度数是15°。
教材P67T1
巩固练习
三
3.算出下面各个未知角的度数。
180°- 65°- 37°=78°
90°- 30°=60°
180°- 25°- 20°=135°
教材P69T1
巩固练习
三
4.求出三角形各个角的度数。
(1)180°÷ 3=60°
三个角都是60°
教材P69T2
巩固练习
三
4.求出三角形各个角的度数。
(2)(180°-96°)÷ 2=42°
三个角分别是96°、42°、42°
教材P69T2
巩固练习
三
4.求出三角形各个角的度数。
(3)180°- 90°- 40°=50°
三个角分别是90°、40°、50°
教材P69T2
巩固练习
三
5.爸爸给小红买了一个等腰三角形的风筝。它的一个底角是70°,它的顶角是多少度?
180°-(70°× 2)=40°
答:它的顶角是40度。
70°
70°
教材P69T3
巩固练习
三
6.在一个等腰三角形中,一个顶角的度数是底角的4倍,这个三角形的顶角与底角各多少度?
1份
1份
4份
底角:180°÷(1+1+4)=30°
顶角:30°× 4=120°
答:这个三角形的顶角是120°,底角是30°。
巩固练习
三
第5课时 多边形的内角和
三角形
5
义务教育人教版四年级下册
连一连。
长方形
正方形
平行四边形
梯形
这些图形的内角和是多少呢?
复习导入
一
四边形的内角和是多少度?
四边形可以分成几种图形
长方形
正方形
平行四边形
梯形
普通四边形
这些图形的内角和是不是一样的呢?
7
阅读与理解
探究新知
二
90?×4=360°
长方形和正方形的4个角都是直角,它们的内角和是360°。
分析与操作
探究新知
二
方法一:测量法
70°+60°+120°+110°=360°
70°
60°
120°
110°
你能想到什么办法求出其他四边形的内角和呢?
探究新知
二
1
1
2
2
4
3
3
4
我把这个四边形的4个角剪下来拼成了一个周角。
方法二:拼图法
探究新知
二
我把这个四边形分成了2个三角形。
一个三角形的内角和是180°,两个相加为360°。
四边形的内角和是_____。
360°
方法三:转化法
探究新知
二
我们大家共同证明了所有四边形的内角和都是360°。
回顾与反思
探究新知
二
你能想办法求出右边这个多边形的内角和吗?
你是怎么想的呢?
提示:将五边形分成三角形再计算!
教材做一做
巩固练习
三
我把这个五边形分成了三个三角形,180?×3=540?。
我把这个五边形分成了5个三角形,把5个三角形的内角加起来再减去中间的一个周角,180?×5-360?=540?。
巩固练习
三
六边形、七边形……的内角和是多少呢?
巩固练习
三
1.画一画,算一算,你发现了什么?
6
7
2
3
180?×4
180?×5
发现:每个多边形都可以分成(边数-2)个三角形,多边形的
内角和=180?×(边数-2)。
教材P69T4
巩固练习
三
2.*下面图形中各有多少个三角形?有什么规律?
1
1+2=3
1+2+3=6
1+2+3+4=10
第n幅图三角形个数为1+2+3+…+(n-1)+n,n为大三角形被分成的三角形个数。
教材P70T7
巩固练习
三
