2020-2021学年人教版九年级下册27.2.1相似三角形的判定(一) 课件(3课时 76张)
文档属性
| 名称 | 2020-2021学年人教版九年级下册27.2.1相似三角形的判定(一) 课件(3课时 76张) |  | |
| 格式 | pptx | ||
| 文件大小 | 633.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-12 10:28:35 | ||
图片预览








文档简介
相似三角形的判定(一)
三边成比例的两个三角形相似
1.复习已经学过的三角形相似的判定定理;
2.掌握利用三边来判定两个三角形相似的方法.(重点、难点)
学习目标
导入新课
回顾与思考
问题 如图,DE∥BC,△ADE∽△ABC?
A
B
C
D
E
类似于判定三角形全等的SSS方法,我们能不能通过三边来判定两个三角形相似呢?
讲授新课
三边成比例的两个三角形相似
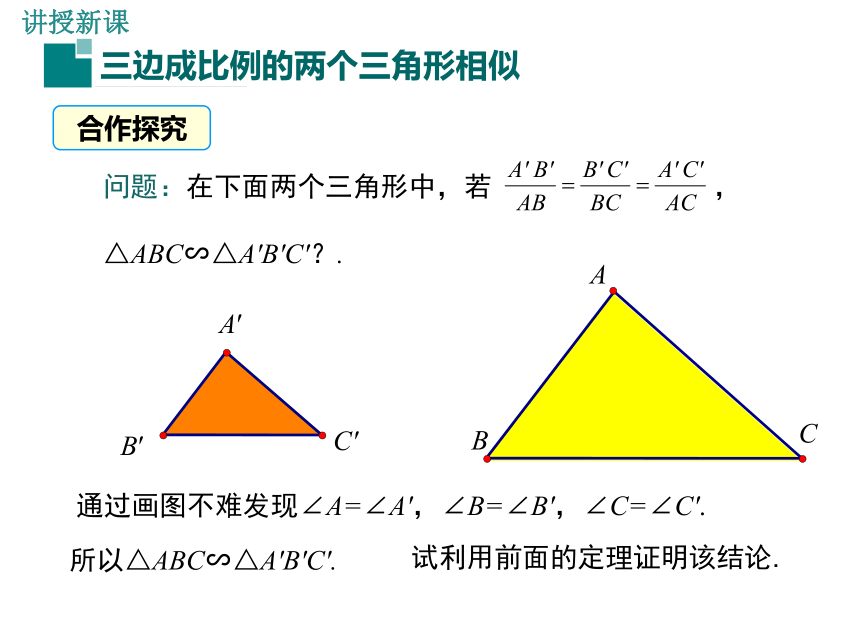
合作探究
问题:在下面两个三角形中,若 ,
△ABC∽△A′B′C′?.
A
B
C
C′
B′
A′
通过画图不难发现∠A=∠A',∠B=∠B',∠C=∠C'.
所以△ABC∽△A′B′C′.
试利用前面的定理证明该结论.
C′
B′
A′
B
C
A
证明:在△ABC的边AB(或延长线)上截取AD=A′B′,
过点D作DE∥BC交AC于点E.
∵A′B′:AB=B′C′:BC=C′A′:CA,
∵ DE∥BC ,∴△ADE∽△ABC.
又∵AD=A′B′,∴AD:AB=A′B′:AB.
∴DE:BC=B′C′:BC, EA:CA=C′A′:CA.
因此DE=B′C′, EA=C′A′.
∴△A′B′C′∽△ABC.
∴△ADE≌△A′B′C′,
D
E
归纳
由此得到三角形的判定定理:
三边成比例的两个三角形相似.
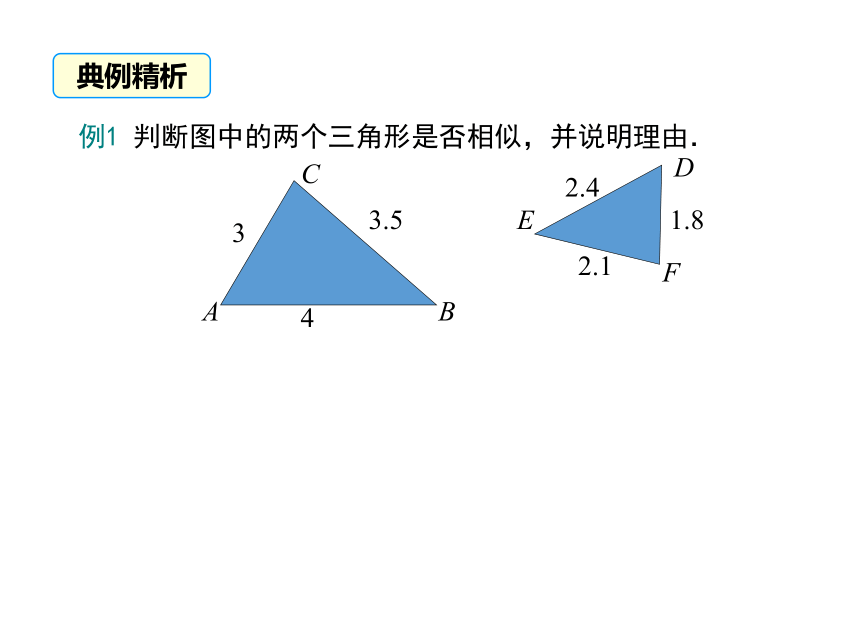
例1 判断图中的两个三角形是否相似,并说明理由.
A
B
C
D
F
E
3
1.8
3.5
2.1
4
2.4
典例精析
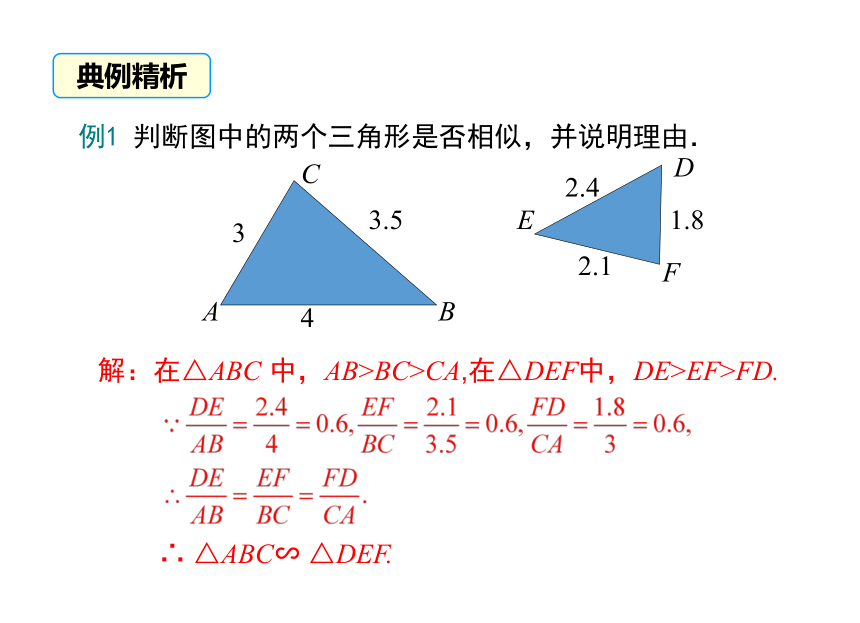
例1 判断图中的两个三角形是否相似,并说明理由.
A
B
C
D
F
E
解:在△ABC 中,AB>BC>CA,在△DEF中,DE>EF>FD.
∴ △ABC∽ △DEF.
3
1.8
3.5
2.1
4
2.4
典例精析
判定三角形相似的方法之一:如果题中给出了两个三角形的三边的长,分别算出三条对应边的比值,看是否相等,计算时最长边与最长边对应,最短边与最短边对应.
方法归纳
已知△ABC 和 △DEF,根据下列条件判断它们是否相似.
(3) AB=12, BC=15, AC=24.
DE=16, EF=20, DF=30.
(2)AB=4, BC=8, AC=10.
DE=20, EF=16, DF=8.
(1)AB=3, BC=4, AC=6.
DE=6, EF=8, DF=9.
练一练
已知△ABC 和 △DEF,根据下列条件判断它们是否相似.
(3) AB=12, BC=15, AC=24.
DE=16, EF=20, DF=30.
(2)AB=4, BC=8, AC=10.
DE=20, EF=16, DF=8.
(1)AB=3, BC=4, AC=6.
DE=6, EF=8, DF=9.
是
否
否
(注意:大对大,小对小,中对中.)
练一练
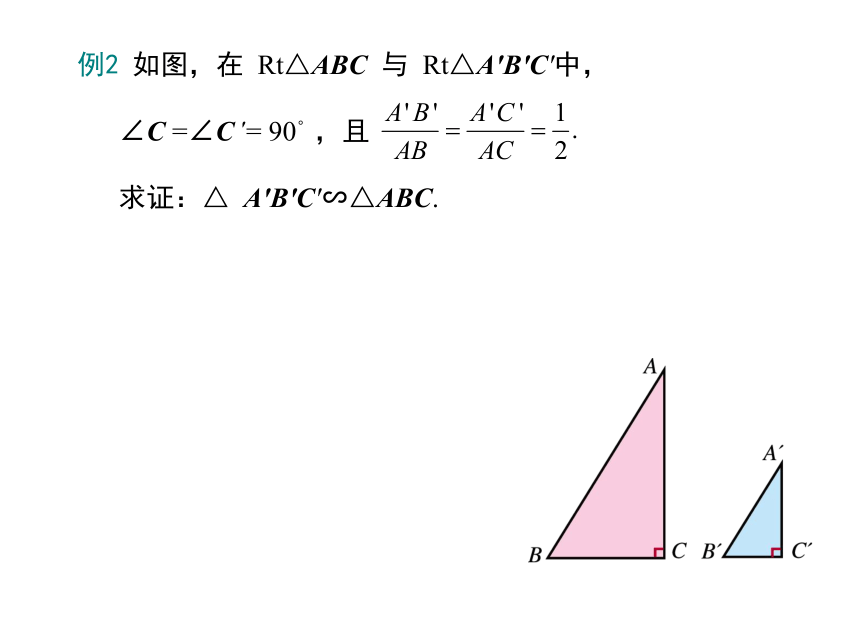
例2 如图,在 Rt△ABC 与 Rt△A′B′C′中,
∠C =∠C ′= 90°,且
求证:△ A′B′C′∽△ABC.
例2 如图,在 Rt△ABC 与 Rt△A′B′C′中,
∠C =∠C ′= 90°,且
求证:△ A′B′C′∽△ABC.
证明:由已知条件得AB=2A′B′,AC=2A′C′
从而
BC2 = AB2-AC2 =(2A′B′)2-(2A′C′)2
= 4A′B′2 – 4A′C′2 =4(A′B′2-A′C′2)
= 4B′C′2 =(2B′C′)2.
从而
由此得出,BC=2B′C′,
因此△ A′B′C′∽△ABC.
(三边对应成比例的两个三角形相似)
例3 如图,在△ABC和△ADE中,
∠BAD=20°,求∠CAE的度数.
A
B
C
D
E
例3 如图,在△ABC和△ADE中,
∠BAD=20°,求∠CAE的度数.
解:∵
∴△ABC∽△ADE(三边成比例的两个三角形相似).
∴∠BAC=∠DAE.
∴∠BAC - ∠DAC =∠DAE-∠DAC.
即 ∠BAD=∠CAE.
∵∠BAD=20°,
∴∠CAE=20°.
A
B
C
D
E
当堂练习
1.根据下列条件,判断△ABC与△A?B?C?是否相似:
AB=4cm ,BC =6cm ,AC =8cm,A?B?=12cm ,
B?C?=18cm ,A?C?=21cm.
当堂练习
1.根据下列条件,判断△ABC与△A?B?C?是否相似:
AB=4cm ,BC =6cm ,AC =8cm,A?B?=12cm ,
B?C?=18cm ,A?C?=21cm.
∴△ABC与△A?B?C?不相似.
2.如图, △ ABC与△ A′B′C′相似吗?你用什么方法来支持你的判断?
C
B
A
A′
B′
C′
2.如图, △ ABC与△ A′B′C′相似吗?你用什么方法来支持你的判断?
C
B
A
A′
B′
C′
解:这两个三角形相似.
设1个小方格的边长为1,则
3.如图,△ABC中,点D、E、F分别是AB、BC、CA的中点,求证:△ABC∽△EFD.
3.如图,△ABC中,点D、E、F分别是AB、BC、CA的中点,求证:△ABC∽△EFD.
∴△ABC∽△EFD.
证明:∵△ABC中,点D、E、F分别是AB、BC、CA的中点,
三边成比例的两个三角形相似
利用三边判定两个三角形相似
课堂小结
相似三角形的判定定理的运用
相似三角形的判定(二)
两边成比例且夹角相等的两个三角形相似
1.探索“两边成比例且夹角相等的两个角形相似”的判定定理;
2.会根据边和角的关系来判定两个三角形相似.(重点、难点)
学习目标
问题1 我们学习过哪些判定三角形全等的方法?
问题2 我们目前知道的两个三角形相似有哪些判定方法?
导入新课
回顾与思考
讲授新课
合作探究
①任意画△ABC;
②再画△A′B′C′,使∠A′=∠A,且
③量出B′C′及BC的长,计算 的值,并比较是否三边都对应成比例?
④量出∠B与∠B′的度数,∠B′=∠B吗?由此可推出∠C′=∠C吗?为什么?
⑤由上面的画图,你能发现△A′B′C′与△ABC有何关系?与你周围的同学交流.
两边成比例且夹角相等的两个三角形相似
我们来证明一下前面得出的结论:
如图,在△ABC与△A′B′C′中,已知∠A= ∠A′
在△A′B′C′的边A′B′上截取点D,使A′D=AB.过点D作DE∥B′C′,交A′C′于点E.
∵DE∥B′C′,
∴△A′DE∽△A′B′C′.
△A′B′C′∽△ABC.
B
A
C
D
E
B'
A'
C'
∵A′D=AB,
∴A′E=AC.
又∠A′=∠A.
∴△A′DE≌△ABC,
∴△A′B′C′∽△ABC.
B
A
C
D
E
B'
A'
C'
由此得到三角形的判定定理:
两边成比例且夹角相等的两个三角形相似.
例1 在△ABC和△DEF中,∠C=∠F=70°,AC=3.5cm,
BC=2.5 cm,DF=2.1 cm,EF=1.5 cm.求证:△DEF∽△ABC.
A
F
E
C
B
D
典例精析
例1 在△ABC和△DEF中,∠C=∠F=70°,AC=3.5cm,
BC=2.5 cm,DF=2.1 cm,EF=1.5 cm.求证:△DEF∽△ABC.
A
F
E
C
B
D
典例精析
证明:
∵AC=3.5cm,BC=2.5cm,DF=2.1cm,EF=1.5cm,
又∵∠C=∠F=70°,
∴ △DEF∽△ABC(两边成比例且夹角相等的两个三角形相似)
?如图,△ABC与△ADE都是等腰三角形,AD=AE,
AB=AC,∠DAB=∠CAE.求证:△ABC∽△ADE.
练一练
?如图,△ABC与△ADE都是等腰三角形,AD=AE,
AB=AC,∠DAB=∠CAE.求证:△ABC∽△ADE.
△ABC∽△ADE.
练一练
证明:
例2 如图,D,E分别是△ABC的边AC,AB上的点,
AE=1.5,AC=2,BC=3,且 ,求DE的长.
A
C
B
E
D
解:∵AE=1.5,AC=2,
∴
∵ ∴
又∵∠EAD=∠CAB,
∴△ADE∽△ABC
∴
∴DE=
例2 如图,D,E分别是△ABC的边AC,AB上的点,
AE=1.5,AC=2,BC=3,且 ,求DE的长.
A
C
B
E
D
例3 如图,在 △ABC 中,CD是边AB上的高,且 求证:∠ACB=90°.
A
B
C
D
例3 如图,在 △ABC 中,CD是边AB上的高,且 求证:∠ACB=90°.
A
B
C
D
证明: ∵ CD是边AB上的高,
∴ ∠ADC= ∠CDB=90°.
∴△ADC∽△CDB.
∴ ∠ACD= ∠B.
∴ ∠ACB= ∠ACD+ ∠BCD= ∠B+ ∠BCD= 90°.
如果两个三角形的两边成比例,但相等的角不是这两边的夹角,那么两个三角形是否相似呢?画一画,量一量.
A
B
C
D
E
F
不相似(类比三角形全等的判定)
探究归纳
归纳:
如果两个三角形两边对应成比例,但相等的角不是两条对应边的夹角,那么两个三角形不一定相似.
注意:相等的角一定要是两条对应边的夹角.
1.判断图中△AEB 和△FEC是否相似?
54
30
36
45
E
A
F
C
B
1
2
当堂练习
(
)
1.判断图中△AEB 和△FEC是否相似?
解:∵
∴△AEB∽△FEC.
∵∠1=∠2,
54
30
36
45
E
A
F
C
B
1
2
∴
当堂练习
(
)
2. 如图,D是△ABC一边BC上一点,连接AD,使 △ABC ∽ △DBA的条件是 ( )
A. AC:BC=AD:BD
B. AC:BC=AB:AD
C. AB2=CD·BC
D. AB2=BD·BC
2. 如图,D是△ABC一边BC上一点,连接AD,使 △ABC ∽ △DBA的条件是 ( )
A. AC:BC=AD:BD
B. AC:BC=AB:AD
C. AB2=CD·BC
D. AB2=BD·BC
D
(
3.如图,在四边形ABCD中,已知∠B=∠ACD,AB=6,BC=4,AC=5,CD= ,求AD的长.
A
B
C
D
△ABC∽△DCA
3.如图,在四边形ABCD中,已知∠B=∠ACD,AB=6,BC=4,AC=5,CD= ,求AD的长.
A
B
C
D
两边成比例且夹角相等的两个三角形相似
利用两边及夹角判定三角形相似
课堂小结
相似三角形的判定定理的运用
相似三角形的判定(三)
两个角分别相等的两个三角形相似
学习目标
1.探索两角分别相等的两个三角形相似的判定定理;
2.掌握利用两角来判定两个三角形相似的方法;(重点、难点)
3.掌握判定两个直角三角形相似的方法.
问题1 观察学生与老师的直角三角板(30°与60°),会相似吗?测量一下,得出你的猜想.
观察与思考
导入新课
问题2 两个人画出两个三角形 ,使三个角分别为60°,45°, 75° .
①分别量出两个三角形三边的长度;
②这两个三角形相似吗?
讲授新课
如图,△ABC与△A′B′C′中,∠A=∠A′, ∠B=∠B′,探究下列问题:
(1)请你借助刻度尺度量AB,BC,AC, A′B′, B′C′, A′C′的长,并计算出它们的比值.由此,你能得到什么?
C
A
A'
B
B'
C'
合作探究
两角分别相等的两个三角形相似
一
(2)试证明△ABC∽△A′B′C′.
证明:在△ABC的边 AB(或AB的延长线)上,截取AD=A′B′,过点 D 作DE//BC,交AC于点 E,则有△ADE∽△ABC,∠ADE=∠B.
∵∠B=∠B′,
∴∠ADE=∠B′.
又∵ AD=A′B′,∠A=∠A′,
∴△ADE≌△A′B′C′,
∴△A′B′C′∽△ABC.
C
A
A'
B
B'
C'
D
E
由此得到相似三角形的判定定理:
两角分别相等的两个三角形相似.
如图,△ABC中,DE∥BC,EF∥AB,
求证:△ADE∽△EFC.
A
E
F
B
C
D
练一练
如图,△ABC中,DE∥BC,EF∥AB,
求证:△ADE∽△EFC.
A
E
F
B
C
D
证明: ∵ DE∥BC,EF∥AB,
∴∠AED=∠C,
∠A=∠FEC.
∴ △ADE∽△EFC.
(两角分别相等的两个三角形相似)
练一练
典例精析
例1.如图,△ABC和△DEF中,∠A=40°,∠B=80°, ∠E=80 ° , ∠F=60 ° .求证:△ABC∽△DEF.
A
F
E
C
B
D
典例精析
例1.如图,△ABC和△DEF中,∠A=40°,∠B=80°, ∠E=80 ° , ∠F=60 ° .求证:△ABC∽△DEF.
A
F
E
C
B
D
证明:∵ 在△ ABC中,∠A=40 ° ,∠B=80 ° ,
∴ ∠C=180 °-∠A-∠B=60 °.
∵ 在△ DEF中,∠E=80 °,∠F=60 °.
∴ ∠B=∠E,∠C=∠F.
∴ △ABC∽△DEF(两角分别相等的
两个三角形相似).
例2 如图,弦AB和CD相交于⊙O内
一点P,求证:PA·PB=PC·PD.
证明:连接AC,DB.
∵∠A和∠D都是弧CB所对的圆周角
∴ ∠A= _______
同理 ∠C= _______
∴ △PAC ∽ △PDB
∴______ 即PA·PB=PC·PD
例2 如图,弦AB和CD相交于⊙O内
一点P,求证:PA·PB=PC·PD.
证明:连接AC,DB.
∵∠A和∠D都是弧CB所对的圆周角
∴ ∠A= _______
同理 ∠C= _______
∴ △PAC ∽ △PDB
∴______ 即PA·PB=PC·PD
∠D
∠B
如图, ∠ABD=∠C, AD=2,AC=8,求AB的长.
A
B
C
D
做一做
如图, ∠ABD=∠C, AD=2,AC=8,求AB的长.
A
B
C
D
解: ∵ ∠ A= ∠ A ,∠ABD=∠C,
∴ △ABD ∽ △ACB .
∴ AB : AC=AD : AB.
∴ AB2= AD · AC.
∵ AD=2,AC=8,
∴ AB =4.
做一做
判定两个直角三角形相似
二
如图,在Rt△ABC和Rt△A'B'C'中,∠C=∠C′=90°.
C
A
A'
B
B'
C'
探究归纳
根据前面的判定定理,不难得知当 或
时,Rt△ABC∽Rt△A'B'C'.
判定两个直角三角形相似
二
如图,在Rt△ABC和Rt△A'B'C'中,∠C=∠C′=90°.
C
A
A'
B
B'
C'
探究归纳
根据前面的判定定理,不难得知当 或
时,Rt△ABC∽Rt△A'B'C'.
∠A=∠A′
∠B=∠B′
由此得到一个判定直角三角形相似的方法:
有一个锐角相等的两个直角三角形相似.
思考:对于两个直角三角形,我们还可以用“HL”判定它们全等,那么,满足斜边和一直角边成比例的两个直角三角形相似吗?
如图,在Rt△ABC和Rt△A′B′C′中,∠C=90°,∠C′=90°,
.
求证: Rt△ABC∽Rt△A′B′C′.
C
A
A'
B
B'
C'
目标:
证明:设____________= k .
由 ,得
∴
∴________
∴Rt △ABC∽Rt △A′B′C′.
勾股定理
C
A
A'
B
B'
C'
由此得到另一个判定直角三角形相似的方法:
斜边和一直角边成比例的两个直角三角形相似.
当堂练习
1.如图,已知AB∥DE,∠AFC=∠E,则图中相似三角形共有( )
A.1对 B.2对
C.3对 D.4对
当堂练习
1.如图,已知AB∥DE,∠AFC=∠E,则图中相似三角形共有( )
A.1对 B.2对
C.3对 D.4对
C
2.如图,△ABC 的高AD、BE交于点F.
求证:
证明: ∵ △ABC 的高AD、BE交于点F,
∴ ∠FEA=∠FDB=90°,∠AFE =∠BFD(对顶角相等).
∴ △FEA ∽ △ FDB,
∴
2.如图,△ABC 的高AD、BE交于点F.
求证:
3.如图,在Rt△ABC中, ∠ABC=90°,BD⊥AC于D.
若 AB=6, AD=2, 则AC= .
BD= .
BC= .
18
D
B
C
A
3.如图,在Rt△ABC中, ∠ABC=90°,BD⊥AC于D.
若 AB=6, AD=2, 则AC= .
BD= .
BC= .
18
D
B
C
A
4.如图,∠1=∠2=∠3,
求证:△ABC∽△ADE.
4.如图,∠1=∠2=∠3,
求证:△ABC∽△ADE.
证明: ∵∠BAC= ∠1+ ∠DAC , ∠DAE= ∠3+ ∠DAC,
∵ ∠1=∠3,∴ ∠BAC=∠DAE.
∵ ∠C=180°-∠2-∠DOC ,∠E=180°-∠3-∠AOE.
又∵ ∠DOC =∠AOE(对顶角相等),
∴ ∠C= ∠E.
∴ △ABC∽△ADE
两角分别相等的两个三角形相似
利用两角判定三角形相似
课堂小结
直角三角形相似的判定
三边成比例的两个三角形相似
1.复习已经学过的三角形相似的判定定理;
2.掌握利用三边来判定两个三角形相似的方法.(重点、难点)
学习目标
导入新课
回顾与思考
问题 如图,DE∥BC,△ADE∽△ABC?
A
B
C
D
E
类似于判定三角形全等的SSS方法,我们能不能通过三边来判定两个三角形相似呢?
讲授新课
三边成比例的两个三角形相似
合作探究
问题:在下面两个三角形中,若 ,
△ABC∽△A′B′C′?.
A
B
C
C′
B′
A′
通过画图不难发现∠A=∠A',∠B=∠B',∠C=∠C'.
所以△ABC∽△A′B′C′.
试利用前面的定理证明该结论.
C′
B′
A′
B
C
A
证明:在△ABC的边AB(或延长线)上截取AD=A′B′,
过点D作DE∥BC交AC于点E.
∵A′B′:AB=B′C′:BC=C′A′:CA,
∵ DE∥BC ,∴△ADE∽△ABC.
又∵AD=A′B′,∴AD:AB=A′B′:AB.
∴DE:BC=B′C′:BC, EA:CA=C′A′:CA.
因此DE=B′C′, EA=C′A′.
∴△A′B′C′∽△ABC.
∴△ADE≌△A′B′C′,
D
E
归纳
由此得到三角形的判定定理:
三边成比例的两个三角形相似.
例1 判断图中的两个三角形是否相似,并说明理由.
A
B
C
D
F
E
3
1.8
3.5
2.1
4
2.4
典例精析
例1 判断图中的两个三角形是否相似,并说明理由.
A
B
C
D
F
E
解:在△ABC 中,AB>BC>CA,在△DEF中,DE>EF>FD.
∴ △ABC∽ △DEF.
3
1.8
3.5
2.1
4
2.4
典例精析
判定三角形相似的方法之一:如果题中给出了两个三角形的三边的长,分别算出三条对应边的比值,看是否相等,计算时最长边与最长边对应,最短边与最短边对应.
方法归纳
已知△ABC 和 △DEF,根据下列条件判断它们是否相似.
(3) AB=12, BC=15, AC=24.
DE=16, EF=20, DF=30.
(2)AB=4, BC=8, AC=10.
DE=20, EF=16, DF=8.
(1)AB=3, BC=4, AC=6.
DE=6, EF=8, DF=9.
练一练
已知△ABC 和 △DEF,根据下列条件判断它们是否相似.
(3) AB=12, BC=15, AC=24.
DE=16, EF=20, DF=30.
(2)AB=4, BC=8, AC=10.
DE=20, EF=16, DF=8.
(1)AB=3, BC=4, AC=6.
DE=6, EF=8, DF=9.
是
否
否
(注意:大对大,小对小,中对中.)
练一练
例2 如图,在 Rt△ABC 与 Rt△A′B′C′中,
∠C =∠C ′= 90°,且
求证:△ A′B′C′∽△ABC.
例2 如图,在 Rt△ABC 与 Rt△A′B′C′中,
∠C =∠C ′= 90°,且
求证:△ A′B′C′∽△ABC.
证明:由已知条件得AB=2A′B′,AC=2A′C′
从而
BC2 = AB2-AC2 =(2A′B′)2-(2A′C′)2
= 4A′B′2 – 4A′C′2 =4(A′B′2-A′C′2)
= 4B′C′2 =(2B′C′)2.
从而
由此得出,BC=2B′C′,
因此△ A′B′C′∽△ABC.
(三边对应成比例的两个三角形相似)
例3 如图,在△ABC和△ADE中,
∠BAD=20°,求∠CAE的度数.
A
B
C
D
E
例3 如图,在△ABC和△ADE中,
∠BAD=20°,求∠CAE的度数.
解:∵
∴△ABC∽△ADE(三边成比例的两个三角形相似).
∴∠BAC=∠DAE.
∴∠BAC - ∠DAC =∠DAE-∠DAC.
即 ∠BAD=∠CAE.
∵∠BAD=20°,
∴∠CAE=20°.
A
B
C
D
E
当堂练习
1.根据下列条件,判断△ABC与△A?B?C?是否相似:
AB=4cm ,BC =6cm ,AC =8cm,A?B?=12cm ,
B?C?=18cm ,A?C?=21cm.
当堂练习
1.根据下列条件,判断△ABC与△A?B?C?是否相似:
AB=4cm ,BC =6cm ,AC =8cm,A?B?=12cm ,
B?C?=18cm ,A?C?=21cm.
∴△ABC与△A?B?C?不相似.
2.如图, △ ABC与△ A′B′C′相似吗?你用什么方法来支持你的判断?
C
B
A
A′
B′
C′
2.如图, △ ABC与△ A′B′C′相似吗?你用什么方法来支持你的判断?
C
B
A
A′
B′
C′
解:这两个三角形相似.
设1个小方格的边长为1,则
3.如图,△ABC中,点D、E、F分别是AB、BC、CA的中点,求证:△ABC∽△EFD.
3.如图,△ABC中,点D、E、F分别是AB、BC、CA的中点,求证:△ABC∽△EFD.
∴△ABC∽△EFD.
证明:∵△ABC中,点D、E、F分别是AB、BC、CA的中点,
三边成比例的两个三角形相似
利用三边判定两个三角形相似
课堂小结
相似三角形的判定定理的运用
相似三角形的判定(二)
两边成比例且夹角相等的两个三角形相似
1.探索“两边成比例且夹角相等的两个角形相似”的判定定理;
2.会根据边和角的关系来判定两个三角形相似.(重点、难点)
学习目标
问题1 我们学习过哪些判定三角形全等的方法?
问题2 我们目前知道的两个三角形相似有哪些判定方法?
导入新课
回顾与思考
讲授新课
合作探究
①任意画△ABC;
②再画△A′B′C′,使∠A′=∠A,且
③量出B′C′及BC的长,计算 的值,并比较是否三边都对应成比例?
④量出∠B与∠B′的度数,∠B′=∠B吗?由此可推出∠C′=∠C吗?为什么?
⑤由上面的画图,你能发现△A′B′C′与△ABC有何关系?与你周围的同学交流.
两边成比例且夹角相等的两个三角形相似
我们来证明一下前面得出的结论:
如图,在△ABC与△A′B′C′中,已知∠A= ∠A′
在△A′B′C′的边A′B′上截取点D,使A′D=AB.过点D作DE∥B′C′,交A′C′于点E.
∵DE∥B′C′,
∴△A′DE∽△A′B′C′.
△A′B′C′∽△ABC.
B
A
C
D
E
B'
A'
C'
∵A′D=AB,
∴A′E=AC.
又∠A′=∠A.
∴△A′DE≌△ABC,
∴△A′B′C′∽△ABC.
B
A
C
D
E
B'
A'
C'
由此得到三角形的判定定理:
两边成比例且夹角相等的两个三角形相似.
例1 在△ABC和△DEF中,∠C=∠F=70°,AC=3.5cm,
BC=2.5 cm,DF=2.1 cm,EF=1.5 cm.求证:△DEF∽△ABC.
A
F
E
C
B
D
典例精析
例1 在△ABC和△DEF中,∠C=∠F=70°,AC=3.5cm,
BC=2.5 cm,DF=2.1 cm,EF=1.5 cm.求证:△DEF∽△ABC.
A
F
E
C
B
D
典例精析
证明:
∵AC=3.5cm,BC=2.5cm,DF=2.1cm,EF=1.5cm,
又∵∠C=∠F=70°,
∴ △DEF∽△ABC(两边成比例且夹角相等的两个三角形相似)
?如图,△ABC与△ADE都是等腰三角形,AD=AE,
AB=AC,∠DAB=∠CAE.求证:△ABC∽△ADE.
练一练
?如图,△ABC与△ADE都是等腰三角形,AD=AE,
AB=AC,∠DAB=∠CAE.求证:△ABC∽△ADE.
△ABC∽△ADE.
练一练
证明:
例2 如图,D,E分别是△ABC的边AC,AB上的点,
AE=1.5,AC=2,BC=3,且 ,求DE的长.
A
C
B
E
D
解:∵AE=1.5,AC=2,
∴
∵ ∴
又∵∠EAD=∠CAB,
∴△ADE∽△ABC
∴
∴DE=
例2 如图,D,E分别是△ABC的边AC,AB上的点,
AE=1.5,AC=2,BC=3,且 ,求DE的长.
A
C
B
E
D
例3 如图,在 △ABC 中,CD是边AB上的高,且 求证:∠ACB=90°.
A
B
C
D
例3 如图,在 △ABC 中,CD是边AB上的高,且 求证:∠ACB=90°.
A
B
C
D
证明: ∵ CD是边AB上的高,
∴ ∠ADC= ∠CDB=90°.
∴△ADC∽△CDB.
∴ ∠ACD= ∠B.
∴ ∠ACB= ∠ACD+ ∠BCD= ∠B+ ∠BCD= 90°.
如果两个三角形的两边成比例,但相等的角不是这两边的夹角,那么两个三角形是否相似呢?画一画,量一量.
A
B
C
D
E
F
不相似(类比三角形全等的判定)
探究归纳
归纳:
如果两个三角形两边对应成比例,但相等的角不是两条对应边的夹角,那么两个三角形不一定相似.
注意:相等的角一定要是两条对应边的夹角.
1.判断图中△AEB 和△FEC是否相似?
54
30
36
45
E
A
F
C
B
1
2
当堂练习
(
)
1.判断图中△AEB 和△FEC是否相似?
解:∵
∴△AEB∽△FEC.
∵∠1=∠2,
54
30
36
45
E
A
F
C
B
1
2
∴
当堂练习
(
)
2. 如图,D是△ABC一边BC上一点,连接AD,使 △ABC ∽ △DBA的条件是 ( )
A. AC:BC=AD:BD
B. AC:BC=AB:AD
C. AB2=CD·BC
D. AB2=BD·BC
2. 如图,D是△ABC一边BC上一点,连接AD,使 △ABC ∽ △DBA的条件是 ( )
A. AC:BC=AD:BD
B. AC:BC=AB:AD
C. AB2=CD·BC
D. AB2=BD·BC
D
(
3.如图,在四边形ABCD中,已知∠B=∠ACD,AB=6,BC=4,AC=5,CD= ,求AD的长.
A
B
C
D
△ABC∽△DCA
3.如图,在四边形ABCD中,已知∠B=∠ACD,AB=6,BC=4,AC=5,CD= ,求AD的长.
A
B
C
D
两边成比例且夹角相等的两个三角形相似
利用两边及夹角判定三角形相似
课堂小结
相似三角形的判定定理的运用
相似三角形的判定(三)
两个角分别相等的两个三角形相似
学习目标
1.探索两角分别相等的两个三角形相似的判定定理;
2.掌握利用两角来判定两个三角形相似的方法;(重点、难点)
3.掌握判定两个直角三角形相似的方法.
问题1 观察学生与老师的直角三角板(30°与60°),会相似吗?测量一下,得出你的猜想.
观察与思考
导入新课
问题2 两个人画出两个三角形 ,使三个角分别为60°,45°, 75° .
①分别量出两个三角形三边的长度;
②这两个三角形相似吗?
讲授新课
如图,△ABC与△A′B′C′中,∠A=∠A′, ∠B=∠B′,探究下列问题:
(1)请你借助刻度尺度量AB,BC,AC, A′B′, B′C′, A′C′的长,并计算出它们的比值.由此,你能得到什么?
C
A
A'
B
B'
C'
合作探究
两角分别相等的两个三角形相似
一
(2)试证明△ABC∽△A′B′C′.
证明:在△ABC的边 AB(或AB的延长线)上,截取AD=A′B′,过点 D 作DE//BC,交AC于点 E,则有△ADE∽△ABC,∠ADE=∠B.
∵∠B=∠B′,
∴∠ADE=∠B′.
又∵ AD=A′B′,∠A=∠A′,
∴△ADE≌△A′B′C′,
∴△A′B′C′∽△ABC.
C
A
A'
B
B'
C'
D
E
由此得到相似三角形的判定定理:
两角分别相等的两个三角形相似.
如图,△ABC中,DE∥BC,EF∥AB,
求证:△ADE∽△EFC.
A
E
F
B
C
D
练一练
如图,△ABC中,DE∥BC,EF∥AB,
求证:△ADE∽△EFC.
A
E
F
B
C
D
证明: ∵ DE∥BC,EF∥AB,
∴∠AED=∠C,
∠A=∠FEC.
∴ △ADE∽△EFC.
(两角分别相等的两个三角形相似)
练一练
典例精析
例1.如图,△ABC和△DEF中,∠A=40°,∠B=80°, ∠E=80 ° , ∠F=60 ° .求证:△ABC∽△DEF.
A
F
E
C
B
D
典例精析
例1.如图,△ABC和△DEF中,∠A=40°,∠B=80°, ∠E=80 ° , ∠F=60 ° .求证:△ABC∽△DEF.
A
F
E
C
B
D
证明:∵ 在△ ABC中,∠A=40 ° ,∠B=80 ° ,
∴ ∠C=180 °-∠A-∠B=60 °.
∵ 在△ DEF中,∠E=80 °,∠F=60 °.
∴ ∠B=∠E,∠C=∠F.
∴ △ABC∽△DEF(两角分别相等的
两个三角形相似).
例2 如图,弦AB和CD相交于⊙O内
一点P,求证:PA·PB=PC·PD.
证明:连接AC,DB.
∵∠A和∠D都是弧CB所对的圆周角
∴ ∠A= _______
同理 ∠C= _______
∴ △PAC ∽ △PDB
∴______ 即PA·PB=PC·PD
例2 如图,弦AB和CD相交于⊙O内
一点P,求证:PA·PB=PC·PD.
证明:连接AC,DB.
∵∠A和∠D都是弧CB所对的圆周角
∴ ∠A= _______
同理 ∠C= _______
∴ △PAC ∽ △PDB
∴______ 即PA·PB=PC·PD
∠D
∠B
如图, ∠ABD=∠C, AD=2,AC=8,求AB的长.
A
B
C
D
做一做
如图, ∠ABD=∠C, AD=2,AC=8,求AB的长.
A
B
C
D
解: ∵ ∠ A= ∠ A ,∠ABD=∠C,
∴ △ABD ∽ △ACB .
∴ AB : AC=AD : AB.
∴ AB2= AD · AC.
∵ AD=2,AC=8,
∴ AB =4.
做一做
判定两个直角三角形相似
二
如图,在Rt△ABC和Rt△A'B'C'中,∠C=∠C′=90°.
C
A
A'
B
B'
C'
探究归纳
根据前面的判定定理,不难得知当 或
时,Rt△ABC∽Rt△A'B'C'.
判定两个直角三角形相似
二
如图,在Rt△ABC和Rt△A'B'C'中,∠C=∠C′=90°.
C
A
A'
B
B'
C'
探究归纳
根据前面的判定定理,不难得知当 或
时,Rt△ABC∽Rt△A'B'C'.
∠A=∠A′
∠B=∠B′
由此得到一个判定直角三角形相似的方法:
有一个锐角相等的两个直角三角形相似.
思考:对于两个直角三角形,我们还可以用“HL”判定它们全等,那么,满足斜边和一直角边成比例的两个直角三角形相似吗?
如图,在Rt△ABC和Rt△A′B′C′中,∠C=90°,∠C′=90°,
.
求证: Rt△ABC∽Rt△A′B′C′.
C
A
A'
B
B'
C'
目标:
证明:设____________= k .
由 ,得
∴
∴________
∴Rt △ABC∽Rt △A′B′C′.
勾股定理
C
A
A'
B
B'
C'
由此得到另一个判定直角三角形相似的方法:
斜边和一直角边成比例的两个直角三角形相似.
当堂练习
1.如图,已知AB∥DE,∠AFC=∠E,则图中相似三角形共有( )
A.1对 B.2对
C.3对 D.4对
当堂练习
1.如图,已知AB∥DE,∠AFC=∠E,则图中相似三角形共有( )
A.1对 B.2对
C.3对 D.4对
C
2.如图,△ABC 的高AD、BE交于点F.
求证:
证明: ∵ △ABC 的高AD、BE交于点F,
∴ ∠FEA=∠FDB=90°,∠AFE =∠BFD(对顶角相等).
∴ △FEA ∽ △ FDB,
∴
2.如图,△ABC 的高AD、BE交于点F.
求证:
3.如图,在Rt△ABC中, ∠ABC=90°,BD⊥AC于D.
若 AB=6, AD=2, 则AC= .
BD= .
BC= .
18
D
B
C
A
3.如图,在Rt△ABC中, ∠ABC=90°,BD⊥AC于D.
若 AB=6, AD=2, 则AC= .
BD= .
BC= .
18
D
B
C
A
4.如图,∠1=∠2=∠3,
求证:△ABC∽△ADE.
4.如图,∠1=∠2=∠3,
求证:△ABC∽△ADE.
证明: ∵∠BAC= ∠1+ ∠DAC , ∠DAE= ∠3+ ∠DAC,
∵ ∠1=∠3,∴ ∠BAC=∠DAE.
∵ ∠C=180°-∠2-∠DOC ,∠E=180°-∠3-∠AOE.
又∵ ∠DOC =∠AOE(对顶角相等),
∴ ∠C= ∠E.
∴ △ABC∽△ADE
两角分别相等的两个三角形相似
利用两角判定三角形相似
课堂小结
直角三角形相似的判定
