2020-2021学年人教版数学七年级下册第五章 相交线与平行线复习课件(23张)
文档属性
| 名称 | 2020-2021学年人教版数学七年级下册第五章 相交线与平行线复习课件(23张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 191.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-12 00:00:00 | ||
图片预览







文档简介
相交线与平行线的复习课
人教版七年级数学第五章相交线与平行线
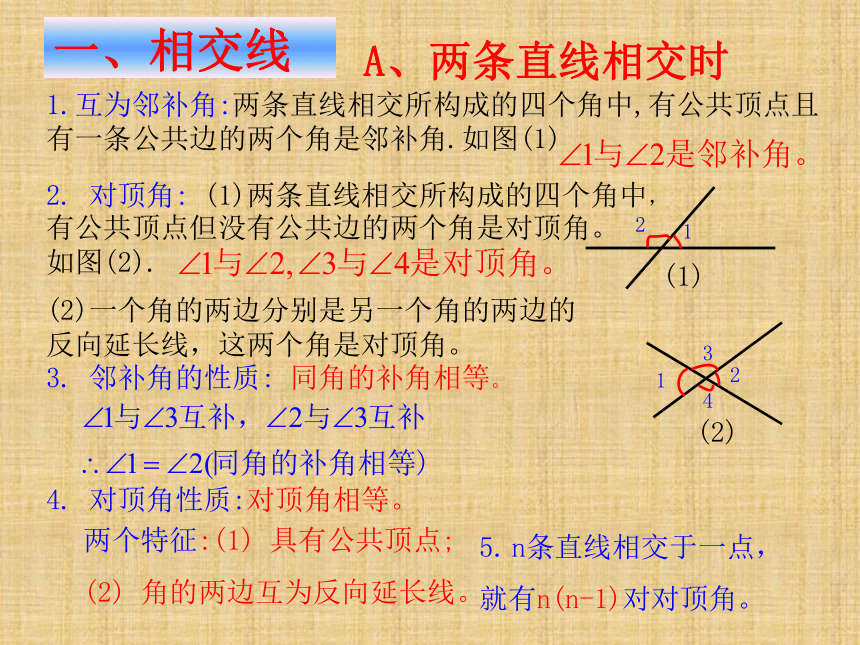
2. 对顶角: (1)两条直线相交所构成的四个角中,
有公共顶点但没有公共边的两个角是对顶角。
如图(2).
(2)一个角的两边分别是另一个角的两边的反向延长线,这两个角是对顶角。
3. 邻补角的性质: 同角的补角相等。
4. 对顶角性质:对顶角相等。
两个特征:(1) 具有公共顶点;
(2) 角的两边互为反向延长线。
n条直线相交于一点,
就有n(n-1)对对顶角。
1
2
(1)
(2)
1
2
3
4
A、两条直线相交时
1.互为邻补角:两条直线相交所构成的四个角中,有公共顶点且有一条公共边的两个角是邻补角.如图(1)
一、相交线
A
B
C
D
O
在解决与角的计算有关的问题时,经常用到代数方法。
解:设∠AOC=2x°,则∠AOD=3x°
所以2x°+3x°=180°
因为∠AOC+∠AOD=180°
解得x=36°
所以∠AOC=2x=72°
∠BOD=∠AOC=72°
答: ∠BOD的度数是72°
例题讲解:
O
A
B
C
D
E
F
1.已知直线AB、CD、EF相交于点O,
解:因为直线AB与EF相交与点O
所以∠AOE+∠BOE=180°
因为∠AOE=36°
所以∠BOE=180°-∠AOE
=180°-36°=144°
因为∠DOE=90°
所以∠AOD=∠AOE+∠DOE=126°
又因为∠BOC与∠AOD是对顶角
所以∠BOC=∠AOD=126°
随堂练习:
1、同位角的位置特征是:
2、内错角的位置特征是:
3、同旁内角的位置特征是:
(1)在截线的同旁,
(2)在被截两直线的同方向。
(1)在截线的两旁,
(2)在被截两直线之间。
(1)在截线的同旁,
(2)在被截两直线之间。
F
1
3
7
5
2
8
6
D
C
A
B
E
4
被截线
截线
三线八角
B、一条直线和两条直线相交时
同位角、内错角、同旁内角,指的是一条直线分别与两条直线相交构成的八个角中,不共顶点的角之间的特殊位置关系。它们与对顶角、邻补角一样,总是成对存在着的。
A
C
B
D
E
1
2
答:∠ EAC
答:∠ DAB
答:∠ BAC,∠BAE , ∠2
∠1与哪个角是同旁内角?
∠2与哪个角是内错角?
1、 ∠1与哪个角是内错角?
随堂练习:
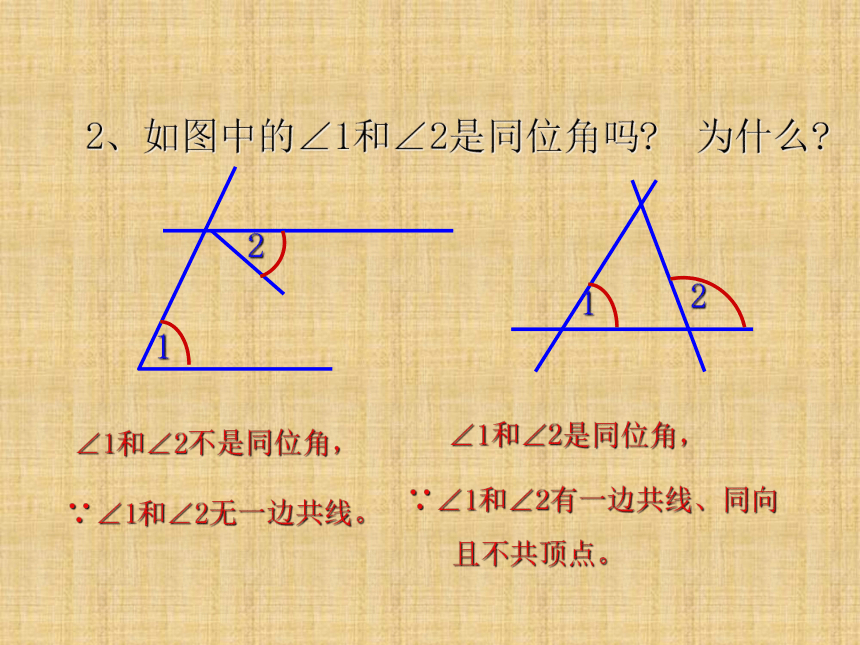
∠1和∠2不是同位角,
2、如图中的∠1和∠2是同位角吗? 为什么?
1
2
1
2
∵∠1和∠2无一边共线。
∠1和∠2是同位角,
∵∠1和∠2有一边共线、同向
且不共顶点。
1.垂线的定义: 两条直线相交,所构成的四个角中,有一个角是90°时,就说这两条直线互相垂直。其中一条直线叫做另一条直线的垂线。它们的交点叫垂足。
2. 垂线的性质: (1)过一点有且只有一条直线与已知直线垂直。(2): 直线外一点与直线上各点连结的所有线段中,垂线段最短。简称:垂线段最短。
3.点到直线的距离: 从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
4.如遇到线段与线段,线段与射线,射线与射线,线段或射线与直线垂直时,特指它们所在的直线互相垂直。
5.垂线是直线,垂线段特指一条线段是图形,点到直线距离是指垂线段的长度,是指一个数量,是有单位的。
二、垂 线
6.垂线的画法:
问题:
这样画l的垂线可以画几条?
1放、
2靠、
3画线、
l
O
如图,已知直线 l,作l的垂线。
工具:直尺、三角板
A
无数条
┓
A
B
C
D
O
E
此题需要正确地
应用、对顶角、
邻补角、垂直的
概念和性质。
例题讲解:
O
A
D
C
B
由垂直先找到90°的角,再根据角之间的关系求解。
(1)定义法;在同一平面内不相交的两条直线是平行线。
(2)传递法;两条直线都和第三条直线平行,这两条直线也平行。
(4)三种角判定
在这六种方法中,定义一般不常用。
同位角相等,两直线平行。
内错角相等,两直线平行。
同旁内角互补,两直线平行。
(3)因为a⊥c, a⊥b;
所以b//c(例题)
a
b
C
F
A
B
C
D
E
1
2
3
4
判定两直线平行的方法有:
三、平行线的判定和性质
两直线平行
条件
结论
同位角相等
内错角相等
同旁内角互补
平
行
线
的
性
质
还有别的性质吗?
证明:由:∠1+∠2=180°(已知)
4
1
2
3
A
B
C
E
F
D
(同旁内角互补,两直线平行)
∠1=∠3(对顶角相等)
∠2=∠4(对顶角相等)
所以∠3+∠4=180°
(等量代换)
AB//CD .
例1. 如图 已知:∠1+∠2=180°,求证:AB∥CD。
例题讲解:
证明: ∵由AC∥DE (已知)
A
D
B
E
1
2
C
∴ ∠ACD= ∠2
(两直线平行,内错角相等)
∵ ∠1=∠2(已知)
∴ ∠1=∠ACD (等量代换)
∴AB ∥ CD
(内错角相等,两直线平行)
1. 如图,已知:AC∥DE,∠1=∠2,试证明AB∥CD。
随堂练习:
1. 命题的概念: 判断一件事情的句子,叫做命题。
命题必须是一个完整的句子; 这个句子必须对某件事情做出肯定或者否定的判断。两者缺一不可。
2. 命题的组成: 每个命题是由题设、结论两部分组成。
题设是已知事项;结论是由已知事项推出的事项。
命题常写成“如果……,那么……”的形式。或 “若……,则……”等形式。
真命题和假命题: 命题是一个判断,这个判断可能是正确的,也可以是错误的。由此可以把命题分成真命题和假命题。
真命题就是: 如果题设成立,那么结论一定成立的命题。
假命题就是: 如果题设成立时,不能保证结论总是成立的命题。
四、命 题
画线段AB=2cm
直角都相等;
两条直线相交,有几个交点?
如果两个角不相等,那么这两个角不是对顶角。
相等的角都是直角;
分析: 因为(1)、(3)不是对某一件事作出判断的句子,所以(1)、(3)不是命题。
解. (1)、(3)不是命题; (2)、(4)、(5)是命题; (2)、(4)都是真命,(5)是假命题。
1. 判断下列语句,是不是命题,如果是命题,是真命题,还是假命题?
随堂练习:
1. 平移变换的定义: 把一个图形整体沿某一方向移动,会得到
一个新图形,这样的图形运动,叫做平移变换,简称平移。
平移的特征: (1)平移不改变图形的形状和大小。
(2)新图形中的每一点,都是由原图形中的某一点移动后得到
的,这两个点是对应点,对应点连结而成的线段平行且相等。
决定平移的因素是平移的方向和距离。
经过平移,图形上的每一点都沿同一方向移动相同的距离。
经过平移,对应角相等;对应线段平行且相等;
对应点所连的线段平行且相等。
五、平 移
站在运动着的电梯上的人
左右推动的推拉窗扇
小李荡秋千运动
躺在火车上睡觉的旅客
分析: A、B、D属平移,在一个位置取两点连成一条线,在另一个位置再观察这条线段,发现是平行的,而C同样取两点连成一条线段,运动到另一位置时,可能已不平行
解: 选C
例1. 在以下生活现象中,不是平移现象的是
例题讲解:
C
∟
理由:垂线段最短
1.如图,要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?请画出图来,并说明理由。
六、巩固提升
证明: ∵ ∠DAC= ∠ACB (已知)
A
B
C
D
E
F
∴ AD// BC
(内错角相等,两直线平行)
∵ ∠D+∠DFE=180°(已知)
∴ AD// EF
(同旁内角互补,两直线平行)
∴ EF// BC
(平行于同一条直线的两条直线互相平行)
2.已知∠DAC= ∠ACB, ∠D+∠DFE=1800,求证:EF//BC
∵ EF⊥AB,CD⊥AB (已知)
∴ EF//CD
(垂直于同一条直线的两条直线互相平行)
∴ ∠EFB= ∠DCB
(两直线平行,同位角相等)
∵ ∠EFB=∠GDC (已知)
∴ ∠DCB=∠GDC (等量代换)
∴ DG∥BC
(内错角相等,两直线平行)
∴ ∠AGD=∠ACB
(两直线平行,同位角相等)
证明:
3.已知EF⊥AB,CD⊥AB,∠EFB=∠GDC,求证:∠AGD=∠ACB。
4.如图所示,△ABC平移到△A′B′C′的位置,则点A的
对应点是____,点B的对应点是____,点C的对应点是____。
线段AB的对应线段是___________,线段BC的对应线段是
______,线段AC的对应线段是_______。∠BAC的对应
角是________,∠ABC的对应角是_________,∠ACB的
对应角是_________。△ABC的平移方向是_____________
___________________________,平移距离是_____________
________________________________。
A
B
C
A′
B′
C′
A′
B′
C′
沿着射线AA′
(或BB′,或CC′)的方向
线段AA′的长
(或线段BB′的长或线段CC′的长
人教版七年级数学第五章相交线与平行线
2. 对顶角: (1)两条直线相交所构成的四个角中,
有公共顶点但没有公共边的两个角是对顶角。
如图(2).
(2)一个角的两边分别是另一个角的两边的反向延长线,这两个角是对顶角。
3. 邻补角的性质: 同角的补角相等。
4. 对顶角性质:对顶角相等。
两个特征:(1) 具有公共顶点;
(2) 角的两边互为反向延长线。
n条直线相交于一点,
就有n(n-1)对对顶角。
1
2
(1)
(2)
1
2
3
4
A、两条直线相交时
1.互为邻补角:两条直线相交所构成的四个角中,有公共顶点且有一条公共边的两个角是邻补角.如图(1)
一、相交线
A
B
C
D
O
在解决与角的计算有关的问题时,经常用到代数方法。
解:设∠AOC=2x°,则∠AOD=3x°
所以2x°+3x°=180°
因为∠AOC+∠AOD=180°
解得x=36°
所以∠AOC=2x=72°
∠BOD=∠AOC=72°
答: ∠BOD的度数是72°
例题讲解:
O
A
B
C
D
E
F
1.已知直线AB、CD、EF相交于点O,
解:因为直线AB与EF相交与点O
所以∠AOE+∠BOE=180°
因为∠AOE=36°
所以∠BOE=180°-∠AOE
=180°-36°=144°
因为∠DOE=90°
所以∠AOD=∠AOE+∠DOE=126°
又因为∠BOC与∠AOD是对顶角
所以∠BOC=∠AOD=126°
随堂练习:
1、同位角的位置特征是:
2、内错角的位置特征是:
3、同旁内角的位置特征是:
(1)在截线的同旁,
(2)在被截两直线的同方向。
(1)在截线的两旁,
(2)在被截两直线之间。
(1)在截线的同旁,
(2)在被截两直线之间。
F
1
3
7
5
2
8
6
D
C
A
B
E
4
被截线
截线
三线八角
B、一条直线和两条直线相交时
同位角、内错角、同旁内角,指的是一条直线分别与两条直线相交构成的八个角中,不共顶点的角之间的特殊位置关系。它们与对顶角、邻补角一样,总是成对存在着的。
A
C
B
D
E
1
2
答:∠ EAC
答:∠ DAB
答:∠ BAC,∠BAE , ∠2
∠1与哪个角是同旁内角?
∠2与哪个角是内错角?
1、 ∠1与哪个角是内错角?
随堂练习:
∠1和∠2不是同位角,
2、如图中的∠1和∠2是同位角吗? 为什么?
1
2
1
2
∵∠1和∠2无一边共线。
∠1和∠2是同位角,
∵∠1和∠2有一边共线、同向
且不共顶点。
1.垂线的定义: 两条直线相交,所构成的四个角中,有一个角是90°时,就说这两条直线互相垂直。其中一条直线叫做另一条直线的垂线。它们的交点叫垂足。
2. 垂线的性质: (1)过一点有且只有一条直线与已知直线垂直。(2): 直线外一点与直线上各点连结的所有线段中,垂线段最短。简称:垂线段最短。
3.点到直线的距离: 从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
4.如遇到线段与线段,线段与射线,射线与射线,线段或射线与直线垂直时,特指它们所在的直线互相垂直。
5.垂线是直线,垂线段特指一条线段是图形,点到直线距离是指垂线段的长度,是指一个数量,是有单位的。
二、垂 线
6.垂线的画法:
问题:
这样画l的垂线可以画几条?
1放、
2靠、
3画线、
l
O
如图,已知直线 l,作l的垂线。
工具:直尺、三角板
A
无数条
┓
A
B
C
D
O
E
此题需要正确地
应用、对顶角、
邻补角、垂直的
概念和性质。
例题讲解:
O
A
D
C
B
由垂直先找到90°的角,再根据角之间的关系求解。
(1)定义法;在同一平面内不相交的两条直线是平行线。
(2)传递法;两条直线都和第三条直线平行,这两条直线也平行。
(4)三种角判定
在这六种方法中,定义一般不常用。
同位角相等,两直线平行。
内错角相等,两直线平行。
同旁内角互补,两直线平行。
(3)因为a⊥c, a⊥b;
所以b//c(例题)
a
b
C
F
A
B
C
D
E
1
2
3
4
判定两直线平行的方法有:
三、平行线的判定和性质
两直线平行
条件
结论
同位角相等
内错角相等
同旁内角互补
平
行
线
的
性
质
还有别的性质吗?
证明:由:∠1+∠2=180°(已知)
4
1
2
3
A
B
C
E
F
D
(同旁内角互补,两直线平行)
∠1=∠3(对顶角相等)
∠2=∠4(对顶角相等)
所以∠3+∠4=180°
(等量代换)
AB//CD .
例1. 如图 已知:∠1+∠2=180°,求证:AB∥CD。
例题讲解:
证明: ∵由AC∥DE (已知)
A
D
B
E
1
2
C
∴ ∠ACD= ∠2
(两直线平行,内错角相等)
∵ ∠1=∠2(已知)
∴ ∠1=∠ACD (等量代换)
∴AB ∥ CD
(内错角相等,两直线平行)
1. 如图,已知:AC∥DE,∠1=∠2,试证明AB∥CD。
随堂练习:
1. 命题的概念: 判断一件事情的句子,叫做命题。
命题必须是一个完整的句子; 这个句子必须对某件事情做出肯定或者否定的判断。两者缺一不可。
2. 命题的组成: 每个命题是由题设、结论两部分组成。
题设是已知事项;结论是由已知事项推出的事项。
命题常写成“如果……,那么……”的形式。或 “若……,则……”等形式。
真命题和假命题: 命题是一个判断,这个判断可能是正确的,也可以是错误的。由此可以把命题分成真命题和假命题。
真命题就是: 如果题设成立,那么结论一定成立的命题。
假命题就是: 如果题设成立时,不能保证结论总是成立的命题。
四、命 题
画线段AB=2cm
直角都相等;
两条直线相交,有几个交点?
如果两个角不相等,那么这两个角不是对顶角。
相等的角都是直角;
分析: 因为(1)、(3)不是对某一件事作出判断的句子,所以(1)、(3)不是命题。
解. (1)、(3)不是命题; (2)、(4)、(5)是命题; (2)、(4)都是真命,(5)是假命题。
1. 判断下列语句,是不是命题,如果是命题,是真命题,还是假命题?
随堂练习:
1. 平移变换的定义: 把一个图形整体沿某一方向移动,会得到
一个新图形,这样的图形运动,叫做平移变换,简称平移。
平移的特征: (1)平移不改变图形的形状和大小。
(2)新图形中的每一点,都是由原图形中的某一点移动后得到
的,这两个点是对应点,对应点连结而成的线段平行且相等。
决定平移的因素是平移的方向和距离。
经过平移,图形上的每一点都沿同一方向移动相同的距离。
经过平移,对应角相等;对应线段平行且相等;
对应点所连的线段平行且相等。
五、平 移
站在运动着的电梯上的人
左右推动的推拉窗扇
小李荡秋千运动
躺在火车上睡觉的旅客
分析: A、B、D属平移,在一个位置取两点连成一条线,在另一个位置再观察这条线段,发现是平行的,而C同样取两点连成一条线段,运动到另一位置时,可能已不平行
解: 选C
例1. 在以下生活现象中,不是平移现象的是
例题讲解:
C
∟
理由:垂线段最短
1.如图,要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?请画出图来,并说明理由。
六、巩固提升
证明: ∵ ∠DAC= ∠ACB (已知)
A
B
C
D
E
F
∴ AD// BC
(内错角相等,两直线平行)
∵ ∠D+∠DFE=180°(已知)
∴ AD// EF
(同旁内角互补,两直线平行)
∴ EF// BC
(平行于同一条直线的两条直线互相平行)
2.已知∠DAC= ∠ACB, ∠D+∠DFE=1800,求证:EF//BC
∵ EF⊥AB,CD⊥AB (已知)
∴ EF//CD
(垂直于同一条直线的两条直线互相平行)
∴ ∠EFB= ∠DCB
(两直线平行,同位角相等)
∵ ∠EFB=∠GDC (已知)
∴ ∠DCB=∠GDC (等量代换)
∴ DG∥BC
(内错角相等,两直线平行)
∴ ∠AGD=∠ACB
(两直线平行,同位角相等)
证明:
3.已知EF⊥AB,CD⊥AB,∠EFB=∠GDC,求证:∠AGD=∠ACB。
4.如图所示,△ABC平移到△A′B′C′的位置,则点A的
对应点是____,点B的对应点是____,点C的对应点是____。
线段AB的对应线段是___________,线段BC的对应线段是
______,线段AC的对应线段是_______。∠BAC的对应
角是________,∠ABC的对应角是_________,∠ACB的
对应角是_________。△ABC的平移方向是_____________
___________________________,平移距离是_____________
________________________________。
A
B
C
A′
B′
C′
A′
B′
C′
沿着射线AA′
(或BB′,或CC′)的方向
线段AA′的长
(或线段BB′的长或线段CC′的长
