鲁教版2020-2021学年七年级数学下册第7章二元一次方程组单元培优训练卷(Word版 含解析)
文档属性
| 名称 | 鲁教版2020-2021学年七年级数学下册第7章二元一次方程组单元培优训练卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 207.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-12 10:44:57 | ||
图片预览




文档简介
第7章二元一次方程组单元培优训练卷
一、选择题
1.不考虑优惠,买1本笔记本和3支水笔共需14元,买4本笔记本和6支水笔共需38元,则购买1本笔记本和1支水笔共需( )
A.3元 B.5元 C.8元 D.13元
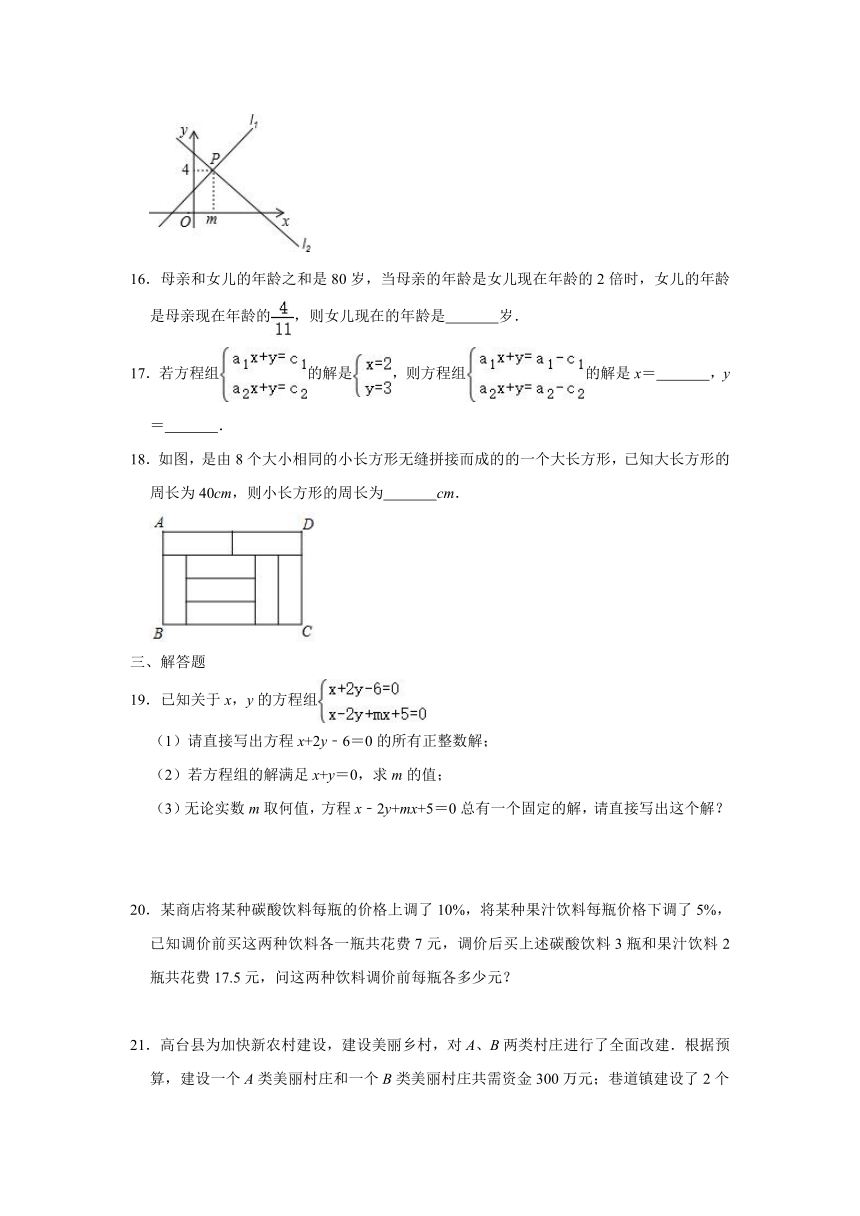
2.已知函数y=ax﹣3和y=kx的图象交于点P(2,﹣1),则关于x,y的二元一次方程组的解是( )
A. B. C. D.
3.若方程组的解x与y的和为2,则m的值为( )
A.﹣2 B.2 C.﹣1 D.1
4.小明要用40元钱买A、B两种型号的口罩,两种型号的口罩必须都买,40元钱全部用尽,A型每个6元,B型口罩每个4元,则小明的购买方案有( ).
A.2种 B.3种 C.4种 D.5种
5.在解方程组由于粗心,甲看错了方程组中的a,得到的解为,乙看错了方程组中的b,得解,则原方程组中的正确的解为( )
A. B. C. D.
6.如图,长方形ABCD被分成3个正方形和2个长方形后仍是中心对称图形,设长方形ABCD的周长为l,若图中3个正方形和2个长方形的周长和为l,则标号为①的正方形的边长为( )
A.l B.l C.l D.l
7.商家常将单价不同的A、B两种糖混合成“什锦糖”出售,记“什锦糖”的单价为:A、B两种糖的总价与A、B两种糖的总质量的比.现有两种“什锦糖”:一种是由相同千克数的A种糖和B种糖混合而成的“什锦糖甲,另一种是由相同金额数的A种糖和B种糖混合而成的“什锦糖乙.若B种糖比A种糖的单价贵40元/千克,“什锦糖”甲比“什锦糖”乙的单价贵5元/千克,则A种糖的单价为( )
A.50元/千克 B.60元/千克 C.70元/千克 D.80元/千克
8.普通火车从绵阳至成都历时大约2小时,成绵城际快车开通后,时间大大缩短至几十分钟,现假定普通火车与城际快车两列对开的火车于同一时刻发车,其中普通火车由成都至绵阳,城际快车由绵阳至成都,这两车在途中相遇之后,各自用了80分钟和20分钟到达自己的终点绵阳、成都,则城际快车的平均速度是普通火车平均速度的( )倍.
A.2 B.2.5 C.3 D.4
二、填空题
9.有甲,乙,丙三种笔,已知买甲种笔2支和乙种1支,丙种3支共12.5元,买甲种1支,乙4支,丙种5支,共18.5元,那么买甲种1支,乙种2支,丙种3支,共需 元.
10.若x=时,关于x,y的二元一次方程组的解x,y互为倒数,则a﹣2b= .
11.如果1台大收割机和1台小收割机每小时各收割小麦x公顷和y公顷,那么2台大收割机和5台小收割机1小时收割小麦 公顷,3台大收割机和2台小收割机1小时收割小麦 公顷.
12.寒假期间,爱学习的小明决定将部分压岁钱用于购买A、B两种文具,2月10日,A文具的单价比B文具的单价少2元,小明购进A、B两种文具共3件;2月20日,A文具的单价翻倍,B文具的单价不变,小明购进A、B两种文具共4件.若A、B文具的单价和数量均为正整数且小明第二次购买文具比第一次购买文具多花费5元,则小明两次购买文具共花费 元.
13.一次考试共需做20个小题,做对一个得8分,做错一个减5分,不做的得0分.某学生共得13分.那么这个学生没有做的题目有 个.
14.小龙和小刚两人玩“打弹珠”游戏,小龙对小刚说:“把你珠子的一半给我,我就有10颗珠子”.小刚却说:“只要把你珠子的给我,我就有10颗”,那么小刚的弹珠颗数是 颗.
15.如图,直线l1:y=x+2与直线l2:y=kx+b相交于点P(m,4),则方程组的解是 .
16.母亲和女儿的年龄之和是80岁,当母亲的年龄是女儿现在年龄的2倍时,女儿的年龄是母亲现在年龄的,则女儿现在的年龄是 岁.
17.若方程组的解是,则方程组的解是x= ,y= .
18.如图,是由8个大小相同的小长方形无缝拼接而成的的一个大长方形,已知大长方形的周长为40cm,则小长方形的周长为 cm.
三、解答题
19.已知关于x,y的方程组
(1)请直接写出方程x+2y﹣6=0的所有正整数解;
(2)若方程组的解满足x+y=0,求m的值;
(3)无论实数m取何值,方程x﹣2y+mx+5=0总有一个固定的解,请直接写出这个解?
20.某商店将某种碳酸饮料每瓶的价格上调了10%,将某种果汁饮料每瓶价格下调了5%,已知调价前买这两种饮料各一瓶共花费7元,调价后买上述碳酸饮料3瓶和果汁饮料2瓶共花费17.5元,问这两种饮料调价前每瓶各多少元?
21.高台县为加快新农村建设,建设美丽乡村,对A、B两类村庄进行了全面改建.根据预算,建设一个A类美丽村庄和一个B类美丽村庄共需资金300万元;巷道镇建设了2个A类村庄和5个B类村庄共投入资金1140万元.
(1)建设一个A类美丽村庄和一个B类美丽村庄所需的资金分别是多少万元?
(2)骆驼城镇改建3个A类美丽村庄和6个B类美丽村庄共需资金多少万元?
22.已知关于x,y的二元一次方程组的解满足方程x﹣2y+1=0,求m的值.
23.面对资源紧缺与环境保护问题,发展电动汽车成为汽车工业发展的主流趋势.我国某著名汽车制造厂开发了一款新式电动汽车,计划一年生产安装240辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人:他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车.
(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?
(2)如果工厂招聘m(0<m<10)名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
(3)在(2)的条件下,工厂给安装电动汽车的每名熟练工每月发8000元的工资,给每名新工人每月发4800元的工资,那么工厂应招聘多少名新工人,使新工人的数量多于熟练工,同时工厂每月支出的工资总额W(元)尽可能的少?
24.已知方程组,甲由于看错了方程①中的a,得到方程组的解为;乙由于看错了方程②中的b,得到方程组的解为;若按正确的a、b计算,求原方程组的解.
参考答案
1.解:设笔记本的单价为x元,水笔的单价为y元,
依题意,得:,
解得:,
∴x+y=8,
即购买1本笔记本和1支水笔共需8元,
故选:C.
2.解:函数y=ax﹣3和y=kx的图象交于点P(2,﹣1),
则关于x,y的二元一次方程组的解是,
故选:B.
3.解:解方程组,得
,
因为x+y=2,
所以m+1+=2,
解得m=1.
则m的值为1.
故选:D.
4.解:设A型x个,B型口罩y个,
可得:6x+4y=40,
因为x,y取正整数,
解得:,,,
所以小明的购买方案有三种,
故选:B.
5.解:将代入x+by=7,将代入ax+y=10,
得 ,
∴,
∴原方程组为
解得,
故选:C.
6.解:长方形ABCD被分成3个正方形和2个长方形后仍是中心对称图形,
∴两个大正方形相同、2个长方形相同.
设两个大正方形边长为y,小正方形的边长为x,
∴小长方形的边长分别为(y﹣x)、(x+y),大长方形边长为(2y﹣x)、(2y+x),
∵大长方形周长=l,即:2[(2y﹣x)+(2y+x)]=l,
∴8y=l,
∴y=
∵3个正方形和2个长方形的周长和为l,
即:,
∴16y+4x=,
∴x=,
则标号为①的正方形的边长,
故选:B.
7.解:设A种糖的单价为x元/千克,则B种糖的单价为(x+40)元/千克,
“什锦糖”甲的单价为(x+x+40)元/千克,
“什锦糖”乙的单价为2÷(+)元/千克,
根据题意,得
(x+x+40)﹣2÷(+)=5,
解得x=60,
经检验x=60是分式方程的解,也符合题意,
所以A种糖的单价为60元/千克.
故选:B.
8.解:设普通火车速度为vm/min,城际快车速度为nvm/min,
已知普通火车从绵阳至成都历时大约2h=120min,由v=可得两地距离:
s=v×120,
普通火车与城际快车两列对开,途中相遇之后,各自用了80分钟和20分钟到达自己的终点绵阳、成都,
即:s普+s城=s,
所以:v×80+nv×20=s,
所以:v×80+nv×20=v×120,
解得:n=2.
故选:A.
9.解:设买1支甲,乙,丙三种笔各a,b,c元.
由题意得,
由②×2﹣①得:b+c=3.5 ③,
由③代入①得:a+c=4.5 ④,
由④+2×③得:a+2b+3c=11.5.
故答案为:11.5.
10.解:由于x、y互为倒数,x=,则y=2,
代入二元一次方程组,
得,
解得a=10,b=﹣,
则a﹣2b=11.
故本题答案为:11.
11.解:由于1台大收割机和1台小收割机1小时各收割小麦x公顷和y公顷.
根据题意得么2台大收割机和5台小收割机1小时收割小麦 (2x+5y)公顷,3台大收割机和2台小收割机1小时收割小麦(3x+2y)公顷.
故答案为(2x+5y),(3x+2y).
12.解:设B文具的单价为x元/件,第一次购买文具共花费y元,
依题意,得:
①当第一次买A文具1个,第二次买A文具1个,
,
解得:,不合题意舍去.
②当第一次买A文具1个,第二次买A文具2个,
,
解得:,不合题意舍去.
③当第一次买A文具1个,第二次买A文具3个
,
解得:,不合题意舍去.
④当第一次买A文具2个,第二次买A文具1个
,
解得:,不合题意舍去.
⑤当第一次买A文具2个,第二次买A文具2个
,
解得:,符合题意.
⑥当第一次买A文具2个,第二次买A文具3个
,
解得,不合题意舍去.
∴x=3,y=5,
∴y+y+5=15.
故答案为:15.
13.解:设该生做对x个题,做错y个题,没做的是z个题.
根据题意列方程组
由①×5+②得 13x+5z=113 ③
根据③式可知,5z的个位数必是0、5,
∴13x的个位数必是3、8,且1≤x≤8
①当x=1时,z=20,不合题意舍去;
②当x=2时,不合题意舍去;
③当x=3时,不合题意舍去;
④当x=4时,不合题意舍去;
⑤当x=5时,不合题意舍去;
⑥当x=6时,z=7,y=7;
⑦当x=7时,不合题意舍去;
⑧当x=8时,不合题意舍去.
故答案为7.
14.解:设小刚的弹珠数是x个,小龙的是y个.
则,
解得,
那么小刚的弹珠颗数是8.
15.解:∵y=x=2经过P(m,4),
∴4=m+2,
∴m=2,
∴直线l1:y=x+2与直线l2:y=kx+b相交于点P(2,4),
∴,
故答案为
16.解:设女儿现在年龄是x岁,母亲现在的年龄是y岁,
根据题意得:,
解得:,
即女儿现在的年龄是25岁,
故答案为:25.
17.解:把代入方程组得,
,
所以c1﹣c2=2(a1﹣a2),c1﹣2a1=3,
方程组,①﹣②得,(a1﹣a2)x=a1﹣a2﹣(c1﹣c2),
所以(a1﹣a2)x=﹣(a1﹣a2),
因此x=﹣1,
把x=﹣1代入方程组中的方程①得,﹣a1+y=a1﹣c1,所以y=2a1﹣c1=﹣(c1﹣2a1)=﹣3,
故答案为:﹣1,﹣3.
18.解:设小长方形的长为xcm,宽为ycm,
由题意知,.
解得,
所以小长方形的周长为:2(6+2)=16(cm).
故答案是:16.
19.解:(1)∵x+2y﹣6=0,∴y=3﹣x
又因为x,y为正整数,
∴3﹣x>0,
即:x只能取2或4;
∴方程x+2y﹣6=0的所有正整数解:,;
(2)由题意得:,解得
把代入x﹣2y+mx+5=0,解得m=﹣;
(3)∵方程x﹣2y+mx+5=0总有一个固定的解,
∴x=0,y=2.5.
∴.
20.解:设碳酸饮料在调价前每瓶的价格为x元,果汁饮料调价前每瓶的价格为y元,
根据题意得:,
解得:.
答:调价前碳酸饮料每瓶的价格为3元,果汁饮料每瓶的价格为4元.
21.解:(1)设建设一个A类美丽村庄所需的资金为x万元,建设一个B类美丽村庄所需的资金为y万元,
,
解得,,
答:建设一个A类美丽村庄和一个B类美丽村庄所需的资金分别是120万元、180万元;
(2)由题意可得,
3×120+6×180=1440(万元),
答:骆驼城镇改建3个A类美丽村庄和6个B类美丽村庄共需资金1440万元.
22.解:,
①+②×2得13x=13m,解得x=m,
把x=m代入①得m+2y=5m,解得y=2m,
把x=m,y=2m代入x﹣2y+1=0得m﹣4m+1=0,
解得m=.
23.解:(1)设每名熟练工和新工人每月分别可以安装x、y辆电动汽车.
根据题意,得:,
解得:.
答:每名熟练工和新工人每月分别可以安装4、2辆电动汽车.
(2)设工厂有a名熟练工.
根据题意,得12(4a+2m)=240,
2a+m=10,
m=10﹣2a,
又a,m都是正整数,0<m<10,
所以m=8,6,4,2.
即工厂有4种新工人的招聘方案.
①m=8,a=1,即新工人8人,熟练工1人;
②m=6,a=2,即新工人6人,熟练工2人;
③m=4,a=3,即新工人4人,熟练工3人;
④m=2,a=4,即新工人2人,熟练工4人.
(3)结合(2)知:要使新工人的数量多于熟练工,则m=8,a=1;或m=6,a=2;或m=4,a=3;
根据题意,得
W=8000a+4800m=8000a+4800(10﹣2a)=48000﹣1600a.
要使工厂每月支出的工资总额W(元)尽可能地少,则a应最大.
显然当m=4,a=3时,工厂每月支出的工资总额W(元)尽可能地少.
24.解:将代入②得,﹣12+b=﹣2,b=10;
将代入①得,5a+20=15,a=﹣1.
故原方程组为,
解得
一、选择题
1.不考虑优惠,买1本笔记本和3支水笔共需14元,买4本笔记本和6支水笔共需38元,则购买1本笔记本和1支水笔共需( )
A.3元 B.5元 C.8元 D.13元
2.已知函数y=ax﹣3和y=kx的图象交于点P(2,﹣1),则关于x,y的二元一次方程组的解是( )
A. B. C. D.
3.若方程组的解x与y的和为2,则m的值为( )
A.﹣2 B.2 C.﹣1 D.1
4.小明要用40元钱买A、B两种型号的口罩,两种型号的口罩必须都买,40元钱全部用尽,A型每个6元,B型口罩每个4元,则小明的购买方案有( ).
A.2种 B.3种 C.4种 D.5种
5.在解方程组由于粗心,甲看错了方程组中的a,得到的解为,乙看错了方程组中的b,得解,则原方程组中的正确的解为( )
A. B. C. D.
6.如图,长方形ABCD被分成3个正方形和2个长方形后仍是中心对称图形,设长方形ABCD的周长为l,若图中3个正方形和2个长方形的周长和为l,则标号为①的正方形的边长为( )
A.l B.l C.l D.l
7.商家常将单价不同的A、B两种糖混合成“什锦糖”出售,记“什锦糖”的单价为:A、B两种糖的总价与A、B两种糖的总质量的比.现有两种“什锦糖”:一种是由相同千克数的A种糖和B种糖混合而成的“什锦糖甲,另一种是由相同金额数的A种糖和B种糖混合而成的“什锦糖乙.若B种糖比A种糖的单价贵40元/千克,“什锦糖”甲比“什锦糖”乙的单价贵5元/千克,则A种糖的单价为( )
A.50元/千克 B.60元/千克 C.70元/千克 D.80元/千克
8.普通火车从绵阳至成都历时大约2小时,成绵城际快车开通后,时间大大缩短至几十分钟,现假定普通火车与城际快车两列对开的火车于同一时刻发车,其中普通火车由成都至绵阳,城际快车由绵阳至成都,这两车在途中相遇之后,各自用了80分钟和20分钟到达自己的终点绵阳、成都,则城际快车的平均速度是普通火车平均速度的( )倍.
A.2 B.2.5 C.3 D.4
二、填空题
9.有甲,乙,丙三种笔,已知买甲种笔2支和乙种1支,丙种3支共12.5元,买甲种1支,乙4支,丙种5支,共18.5元,那么买甲种1支,乙种2支,丙种3支,共需 元.
10.若x=时,关于x,y的二元一次方程组的解x,y互为倒数,则a﹣2b= .
11.如果1台大收割机和1台小收割机每小时各收割小麦x公顷和y公顷,那么2台大收割机和5台小收割机1小时收割小麦 公顷,3台大收割机和2台小收割机1小时收割小麦 公顷.
12.寒假期间,爱学习的小明决定将部分压岁钱用于购买A、B两种文具,2月10日,A文具的单价比B文具的单价少2元,小明购进A、B两种文具共3件;2月20日,A文具的单价翻倍,B文具的单价不变,小明购进A、B两种文具共4件.若A、B文具的单价和数量均为正整数且小明第二次购买文具比第一次购买文具多花费5元,则小明两次购买文具共花费 元.
13.一次考试共需做20个小题,做对一个得8分,做错一个减5分,不做的得0分.某学生共得13分.那么这个学生没有做的题目有 个.
14.小龙和小刚两人玩“打弹珠”游戏,小龙对小刚说:“把你珠子的一半给我,我就有10颗珠子”.小刚却说:“只要把你珠子的给我,我就有10颗”,那么小刚的弹珠颗数是 颗.
15.如图,直线l1:y=x+2与直线l2:y=kx+b相交于点P(m,4),则方程组的解是 .
16.母亲和女儿的年龄之和是80岁,当母亲的年龄是女儿现在年龄的2倍时,女儿的年龄是母亲现在年龄的,则女儿现在的年龄是 岁.
17.若方程组的解是,则方程组的解是x= ,y= .
18.如图,是由8个大小相同的小长方形无缝拼接而成的的一个大长方形,已知大长方形的周长为40cm,则小长方形的周长为 cm.
三、解答题
19.已知关于x,y的方程组
(1)请直接写出方程x+2y﹣6=0的所有正整数解;
(2)若方程组的解满足x+y=0,求m的值;
(3)无论实数m取何值,方程x﹣2y+mx+5=0总有一个固定的解,请直接写出这个解?
20.某商店将某种碳酸饮料每瓶的价格上调了10%,将某种果汁饮料每瓶价格下调了5%,已知调价前买这两种饮料各一瓶共花费7元,调价后买上述碳酸饮料3瓶和果汁饮料2瓶共花费17.5元,问这两种饮料调价前每瓶各多少元?
21.高台县为加快新农村建设,建设美丽乡村,对A、B两类村庄进行了全面改建.根据预算,建设一个A类美丽村庄和一个B类美丽村庄共需资金300万元;巷道镇建设了2个A类村庄和5个B类村庄共投入资金1140万元.
(1)建设一个A类美丽村庄和一个B类美丽村庄所需的资金分别是多少万元?
(2)骆驼城镇改建3个A类美丽村庄和6个B类美丽村庄共需资金多少万元?
22.已知关于x,y的二元一次方程组的解满足方程x﹣2y+1=0,求m的值.
23.面对资源紧缺与环境保护问题,发展电动汽车成为汽车工业发展的主流趋势.我国某著名汽车制造厂开发了一款新式电动汽车,计划一年生产安装240辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人:他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车.
(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?
(2)如果工厂招聘m(0<m<10)名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
(3)在(2)的条件下,工厂给安装电动汽车的每名熟练工每月发8000元的工资,给每名新工人每月发4800元的工资,那么工厂应招聘多少名新工人,使新工人的数量多于熟练工,同时工厂每月支出的工资总额W(元)尽可能的少?
24.已知方程组,甲由于看错了方程①中的a,得到方程组的解为;乙由于看错了方程②中的b,得到方程组的解为;若按正确的a、b计算,求原方程组的解.
参考答案
1.解:设笔记本的单价为x元,水笔的单价为y元,
依题意,得:,
解得:,
∴x+y=8,
即购买1本笔记本和1支水笔共需8元,
故选:C.
2.解:函数y=ax﹣3和y=kx的图象交于点P(2,﹣1),
则关于x,y的二元一次方程组的解是,
故选:B.
3.解:解方程组,得
,
因为x+y=2,
所以m+1+=2,
解得m=1.
则m的值为1.
故选:D.
4.解:设A型x个,B型口罩y个,
可得:6x+4y=40,
因为x,y取正整数,
解得:,,,
所以小明的购买方案有三种,
故选:B.
5.解:将代入x+by=7,将代入ax+y=10,
得 ,
∴,
∴原方程组为
解得,
故选:C.
6.解:长方形ABCD被分成3个正方形和2个长方形后仍是中心对称图形,
∴两个大正方形相同、2个长方形相同.
设两个大正方形边长为y,小正方形的边长为x,
∴小长方形的边长分别为(y﹣x)、(x+y),大长方形边长为(2y﹣x)、(2y+x),
∵大长方形周长=l,即:2[(2y﹣x)+(2y+x)]=l,
∴8y=l,
∴y=
∵3个正方形和2个长方形的周长和为l,
即:,
∴16y+4x=,
∴x=,
则标号为①的正方形的边长,
故选:B.
7.解:设A种糖的单价为x元/千克,则B种糖的单价为(x+40)元/千克,
“什锦糖”甲的单价为(x+x+40)元/千克,
“什锦糖”乙的单价为2÷(+)元/千克,
根据题意,得
(x+x+40)﹣2÷(+)=5,
解得x=60,
经检验x=60是分式方程的解,也符合题意,
所以A种糖的单价为60元/千克.
故选:B.
8.解:设普通火车速度为vm/min,城际快车速度为nvm/min,
已知普通火车从绵阳至成都历时大约2h=120min,由v=可得两地距离:
s=v×120,
普通火车与城际快车两列对开,途中相遇之后,各自用了80分钟和20分钟到达自己的终点绵阳、成都,
即:s普+s城=s,
所以:v×80+nv×20=s,
所以:v×80+nv×20=v×120,
解得:n=2.
故选:A.
9.解:设买1支甲,乙,丙三种笔各a,b,c元.
由题意得,
由②×2﹣①得:b+c=3.5 ③,
由③代入①得:a+c=4.5 ④,
由④+2×③得:a+2b+3c=11.5.
故答案为:11.5.
10.解:由于x、y互为倒数,x=,则y=2,
代入二元一次方程组,
得,
解得a=10,b=﹣,
则a﹣2b=11.
故本题答案为:11.
11.解:由于1台大收割机和1台小收割机1小时各收割小麦x公顷和y公顷.
根据题意得么2台大收割机和5台小收割机1小时收割小麦 (2x+5y)公顷,3台大收割机和2台小收割机1小时收割小麦(3x+2y)公顷.
故答案为(2x+5y),(3x+2y).
12.解:设B文具的单价为x元/件,第一次购买文具共花费y元,
依题意,得:
①当第一次买A文具1个,第二次买A文具1个,
,
解得:,不合题意舍去.
②当第一次买A文具1个,第二次买A文具2个,
,
解得:,不合题意舍去.
③当第一次买A文具1个,第二次买A文具3个
,
解得:,不合题意舍去.
④当第一次买A文具2个,第二次买A文具1个
,
解得:,不合题意舍去.
⑤当第一次买A文具2个,第二次买A文具2个
,
解得:,符合题意.
⑥当第一次买A文具2个,第二次买A文具3个
,
解得,不合题意舍去.
∴x=3,y=5,
∴y+y+5=15.
故答案为:15.
13.解:设该生做对x个题,做错y个题,没做的是z个题.
根据题意列方程组
由①×5+②得 13x+5z=113 ③
根据③式可知,5z的个位数必是0、5,
∴13x的个位数必是3、8,且1≤x≤8
①当x=1时,z=20,不合题意舍去;
②当x=2时,不合题意舍去;
③当x=3时,不合题意舍去;
④当x=4时,不合题意舍去;
⑤当x=5时,不合题意舍去;
⑥当x=6时,z=7,y=7;
⑦当x=7时,不合题意舍去;
⑧当x=8时,不合题意舍去.
故答案为7.
14.解:设小刚的弹珠数是x个,小龙的是y个.
则,
解得,
那么小刚的弹珠颗数是8.
15.解:∵y=x=2经过P(m,4),
∴4=m+2,
∴m=2,
∴直线l1:y=x+2与直线l2:y=kx+b相交于点P(2,4),
∴,
故答案为
16.解:设女儿现在年龄是x岁,母亲现在的年龄是y岁,
根据题意得:,
解得:,
即女儿现在的年龄是25岁,
故答案为:25.
17.解:把代入方程组得,
,
所以c1﹣c2=2(a1﹣a2),c1﹣2a1=3,
方程组,①﹣②得,(a1﹣a2)x=a1﹣a2﹣(c1﹣c2),
所以(a1﹣a2)x=﹣(a1﹣a2),
因此x=﹣1,
把x=﹣1代入方程组中的方程①得,﹣a1+y=a1﹣c1,所以y=2a1﹣c1=﹣(c1﹣2a1)=﹣3,
故答案为:﹣1,﹣3.
18.解:设小长方形的长为xcm,宽为ycm,
由题意知,.
解得,
所以小长方形的周长为:2(6+2)=16(cm).
故答案是:16.
19.解:(1)∵x+2y﹣6=0,∴y=3﹣x
又因为x,y为正整数,
∴3﹣x>0,
即:x只能取2或4;
∴方程x+2y﹣6=0的所有正整数解:,;
(2)由题意得:,解得
把代入x﹣2y+mx+5=0,解得m=﹣;
(3)∵方程x﹣2y+mx+5=0总有一个固定的解,
∴x=0,y=2.5.
∴.
20.解:设碳酸饮料在调价前每瓶的价格为x元,果汁饮料调价前每瓶的价格为y元,
根据题意得:,
解得:.
答:调价前碳酸饮料每瓶的价格为3元,果汁饮料每瓶的价格为4元.
21.解:(1)设建设一个A类美丽村庄所需的资金为x万元,建设一个B类美丽村庄所需的资金为y万元,
,
解得,,
答:建设一个A类美丽村庄和一个B类美丽村庄所需的资金分别是120万元、180万元;
(2)由题意可得,
3×120+6×180=1440(万元),
答:骆驼城镇改建3个A类美丽村庄和6个B类美丽村庄共需资金1440万元.
22.解:,
①+②×2得13x=13m,解得x=m,
把x=m代入①得m+2y=5m,解得y=2m,
把x=m,y=2m代入x﹣2y+1=0得m﹣4m+1=0,
解得m=.
23.解:(1)设每名熟练工和新工人每月分别可以安装x、y辆电动汽车.
根据题意,得:,
解得:.
答:每名熟练工和新工人每月分别可以安装4、2辆电动汽车.
(2)设工厂有a名熟练工.
根据题意,得12(4a+2m)=240,
2a+m=10,
m=10﹣2a,
又a,m都是正整数,0<m<10,
所以m=8,6,4,2.
即工厂有4种新工人的招聘方案.
①m=8,a=1,即新工人8人,熟练工1人;
②m=6,a=2,即新工人6人,熟练工2人;
③m=4,a=3,即新工人4人,熟练工3人;
④m=2,a=4,即新工人2人,熟练工4人.
(3)结合(2)知:要使新工人的数量多于熟练工,则m=8,a=1;或m=6,a=2;或m=4,a=3;
根据题意,得
W=8000a+4800m=8000a+4800(10﹣2a)=48000﹣1600a.
要使工厂每月支出的工资总额W(元)尽可能地少,则a应最大.
显然当m=4,a=3时,工厂每月支出的工资总额W(元)尽可能地少.
24.解:将代入②得,﹣12+b=﹣2,b=10;
将代入①得,5a+20=15,a=﹣1.
故原方程组为,
解得
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
