7.1 两条直线的位置关系课件(共40张PPT)
文档属性
| 名称 | 7.1 两条直线的位置关系课件(共40张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-12 00:00:00 | ||
图片预览








文档简介
第七章 相交线与平行线
1 两条直线的位置关系
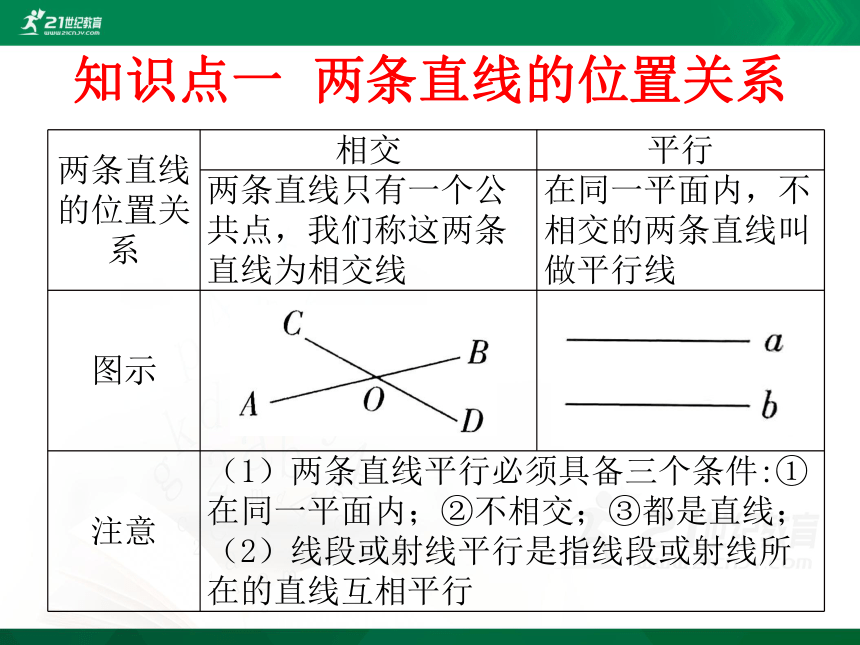
知识点一 两条直线的位置关系
两条直线的位置关系
相交
平行
图示
注意
知识点一 两条直线的位置关系
两条直线的位置关系
相交
平行
两条直线只有一个公共点,我们称这两条直线为相交线
在同一平面内,不相交的两条直线叫做平行线
图示
注意
(1)两条直线平行必须具备三个条件:①在同一平面内;②不相交;③都是直线;(2)线段或射线平行是指线段或射线所在的直线互相平行
例1 下列说法正确的是( )
A.同一平面内没有公共点的两条线段平行
B.两条不相交的直线是平行线
C.同一平面内没有公共点的两条直线平行
D.同一平面内没有公共点的两条射线平行
例1 下列说法正确的是( )
A.同一平面内没有公共点的两条线段平行
B.两条不相交的直线是平行线
C.同一平面内没有公共点的两条直线平行
D.同一平面内没有公共点的两条射线平行
解析 两条线段虽然没有交点,但它们所在的直线可能有交点,A错误.若两条不相交的直线在不同的平面内,则这两条直线也不是平行线,B错误.选项C符合两直线平行的三个条件:①是直线;②在同一平面内;③没有交点两条射线虽然没有交点,但它们所在的直线可能有交点,D错误.
例1 下列说法正确的是( )
A.同一平面内没有公共点的两条线段平行
B.两条不相交的直线是平行线
C.同一平面内没有公共点的两条直线平行
D.同一平面内没有公共点的两条射线平行
解析 两条线段虽然没有交点,但它们所在的直线可能有交点,A错误.若两条不相交的直线在不同的平面内,则这两条直线也不是平行线,B错误.选项C符合两直线平行的三个条件:①是直线;②在同一平面内;③没有交点两条射线虽然没有交点,但它们所在的直线可能有交点,D错误.
答案 C
知识点二 对顶角及其性质
定义
性质
图例
对顶角
拓展延伸
温馨提示
知识点二 对顶角及其性质
定义
性质
图例
对顶角
有一个公共顶点,并且一个角的两边分别是另一个角两边的反向延长线.具有这种位置关系的两个角互为对顶角
对顶角相等.如图,
∠1=∠3,∠2=∠4
拓展延伸
(1)两条直线相交形成两对对顶角.(2)判断两个角是不是对顶角,应抓住两点:一是两个角是否有公共顶点,二是两角的两边是否分别互为反向延长线
温馨提示
对顶角相等,但相等的角不一定是对顶角
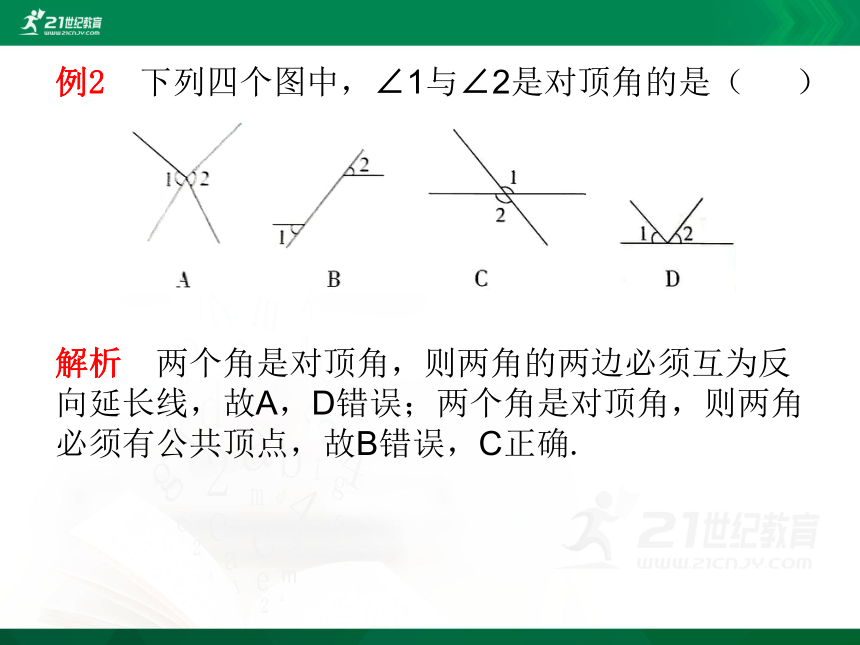
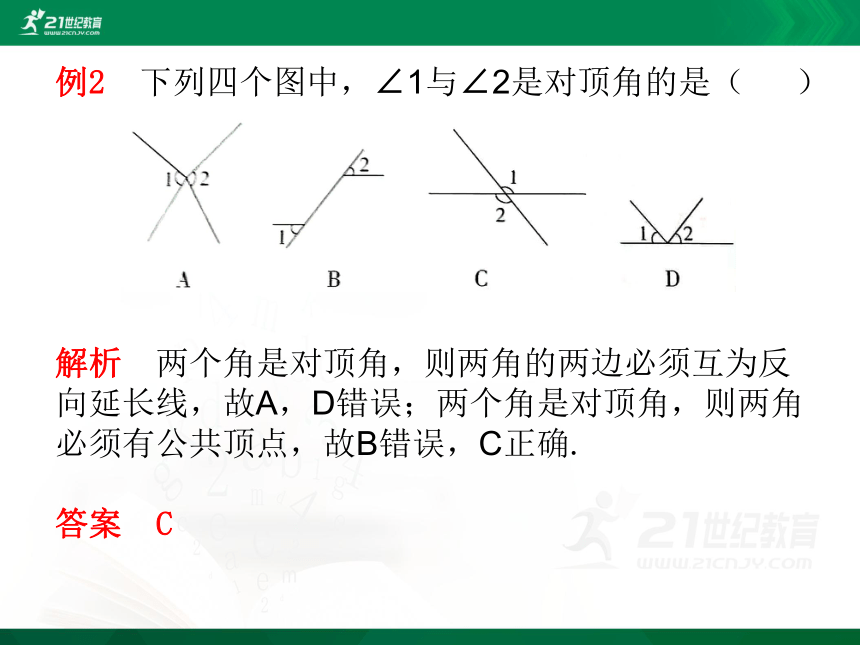
例2 下列四个图中,∠1与∠2是对顶角的是( )
例2 下列四个图中,∠1与∠2是对顶角的是( )
解析 两个角是对顶角,则两角的两边必须互为反向延长线,故A,D错误;两个角是对顶角,则两角必须有公共顶点,故B错误,C正确.
例2 下列四个图中,∠1与∠2是对顶角的是( )
解析 两个角是对顶角,则两角的两边必须互为反向延长线,故A,D错误;两个角是对顶角,则两角必须有公共顶点,故B错误,C正确.
答案 C
知识点三 互余、互补及其性质
互补
互余
定义
性质
注意
知识点三 互余、互补及其性质
互补
互余
定义
两个角的和是180°
两个角的和是90°
性质
同角或等角的补角相等
同角或等角的余角相等
注意
(1)互余、互补是指两个角之间的数量关系,与两个角的位置无关.
(2)互余的两个角都是锐角,而互补的两个角可能一个是锐角、一个是钝角,也可能都是直角
例3 如图所示,O是直线AB上一点,∠AOC=∠BOC=∠DOE=90°.
(1)图中互为余角的角有几对?各是哪些?
(2)∠1的余角是哪些?
(3)图中互为补角的角有几对?各是哪些?
(4)∠1的补角是哪个?
解析 (1)互为余角的角有4对,分别是∠1与∠2,∠3与∠4,∠2与∠3,∠1与∠4.
(2)由∠1+∠2=90°,∠1+∠4=90°得,∠1的余角是∠2和∠4.
(3)互为补角的角有7对,分别是∠1与∠BOD,∠AOC与∠BOC,∠4与∠AOE,∠3与∠BOD,∠2与∠AOE,∠DOE与∠AOC,∠DOE与∠BOC.
(4)由∠1+∠BOD=180°得,∠1的补角是∠BOD.
知识点四 垂直及垂线的画法
1.垂直的相关定义
定义
符号语言
图例
垂直
拓展延伸
知识点四 垂直及垂线的画法
1.垂直的相关定义
定义
符号语言
图例
垂直
两条直线相交所成的四个角中有一个角为90°时,这两条直线互相垂直其中一条直线是另一条直线的垂线,它们的交点叫垂足
如图,∠AOC=90°或∠BOC=90°或∠AOD=90°或∠BOD=90° AB⊥CD
拓展延伸
(1)垂直是两条直线相交的特殊情况,特殊在夹角为90°.(2)垂直的定义具有双重作用,即已知夹角为直角可以得到两直线垂直(判定);由两直线垂直可以得到夹角为90°(性质)
2.垂线的画法
画垂线
的方法
温馨提示
2.垂线的画法
画垂线的方法
用三角尺画垂线
“一靠、二过、三画”,即第一步:把三角尺的一条直角边靠在已知直线上;第二步:使三角尺的另一条直角边经过已知点;第三步:沿已知点所在的直角边画出直线
用直尺画垂线、用量角器画垂线、用折纸的方法折出垂线
温馨提示
(1)过一点画射线或线段的垂线,是指画它们所在直线的垂线,垂足可能在射线的反向延长线或线段的延长线上.(2)画垂线时是实线,如需延长线段或反向延长射线,则用虚线
例4 已知:如图所示,直线AB,CD相交于点O,OE⊥CD于点O,∠BOD=40°.求∠AOE的度数.
例4 已知:如图所示,直线AB,CD相交于点O,OE⊥CD于点O,∠BOD=40°.求∠AOE的度数.
解析 因为OE⊥CD,
所以∠DOE=90°,
因为∠BOD=40°,
所以∠AOE=180°-90°-40°=50°.
知识点五 垂线段及性质
1.垂线段
定义
图形
识记
垂
线
段
拓展延伸
知识点五 垂线段及性质
1.垂线段
定义
图形
识记
垂
线
段
连接直线 外一点A与直线 上各点的线段中,与直线 垂直的线段叫做点A到直线 的垂线段
线段AO是直线的垂线段.
线段AO的长度叫做点A到直线
的距离
拓展延伸
(1)垂线是直线,垂线段是线段
(2)斜线段有无数条,但垂线段只有一条
2.性质
性质一
性质二
内容
拓展延伸
2.性质
性质一
性质二
内容
在同一平面内,过一点有且只有一条直线与已知直线垂直
直线外一点与直线上各点连接的所有线段中,垂线段最短
拓展延伸
(1)有且只有“说明了垂线的存在性和唯一性.(2)“过一点”中的这一点,可以在已知直线上,也可以在已知直线外
(1)垂线段是一条线段,它是有长度的.(2)“一点”必须在直线外,若这点在直线上,就构不成垂线段,故这一点不能在直线上
例5 下列图形中,线段PQ的长表示点P到直线MN的距离的是( )
例5 下列图形中,线段PQ的长表示点P到直线MN的距离的是( )
解析 根据点到直线的距离的概念可知,线段PQ的长表示点P到直线MN的距离的是A.
例5 下列图形中,线段PQ的长表示点P到直线MN的距离的是( )
解析 根据点到直线的距离的概念可知,线段PQ的长表示点P到直线MN的距离的是A.
答案 A
经典例题
题型一 与对顶角有关的计算
例1 如图所示,三条直线 AB CDEF交于点O,已知∠3=3∠2、∠2=2∠1,求∠1、∠2、∠3的大小.
题型一 与对顶角有关的计算
例1 如图所示,三条直线 AB CDEF交于点O,已知∠3=3∠2、∠2=2∠1,求∠1、∠2、∠3的大小.
分析 根据∠2=∠FOD,∠1+∠FOD+∠3=180°,建立等量系求解.
题型一 与对顶角有关的计算
例1 如图所示,三条直线 AB CDEF交于点O,已知∠3=3∠2、∠2=2∠1,求∠1、∠2、∠3的大小.
分析 根据∠2=∠FOD,∠1+∠FOD+∠3=180°,建立等量系求解.
解析 设∠1=x°,则∠2=2∠1=2x°,∴∠3=3∠2=6x°,因为∠2=∠FOD,∠1+∠FOD+∠3=180°,所以x+2x+6x=180,解得x=20,∴∠1=20°,∠2=40°,∠3=120°.
题型一 与对顶角有关的计算
例1 如图所示,三条直线 AB CDEF交于点O,已知∠3=3∠2、∠2=2∠1,求∠1、∠2、∠3的大小.
分析 根据∠2=∠FOD,∠1+∠FOD+∠3=180°,建立等量系求解.
解析 设∠1=x°,则∠2=2∠1=2x°,∴∠3=3∠2=6x°,因为∠2=∠FOD,∠1+∠FOD+∠3=180°,所以x+2x+6x=180,解得x=20,∴∠1=20°,∠2=40°,∠3=120°.
点拨 本题的隐含条件是平角等于180度.当题目中没有角的具体度数,却需要求某些角的度数时,往往借助隐含条件解决问题.
题型二 与互余或互补有关的计算
例2 如图所示,∠AOB与∠BOD互为余角,OB是∠AOC的平分线,∠AOB=25°,求∠CODB的度数.
题型二 与互余或互补有关的计算
例2 如图所示,∠AOB与∠BOD互为余角,OB是∠AOC的平分线,∠AOB=25°,求∠CODB的度数.
解析 因为OB是∠AOC的平分线,∠AOB=25°,所以∠BOC=∠AOB=25°,因为∠AOB与∠BOD互为余角,所以∠BOD=90°-∠AOB=90°-25°=65°,所以∠COD=∠BOD-∠BOC=65°-25°=40°.
题型三 垂线段性质的运用
例3 如图所示,村庄A、村庄B分别要
从河流L引水入庄,各需修筑一条水渠,
请你画出修筑水渠的最短路线图.
题型三 垂线段性质的运用
例3 如图所示,村庄A、村庄B分别要
从河流L引水入庄,各需修筑一条水渠,
请你画出修筑水渠的最短路线图.
分析 根据垂线段最短,分别过点A、B作河流的垂线段即可.
题型三 垂线段性质的运用
例3 如图所示,村庄A、村庄B分别要
从河流L引水入庄,各需修筑一条水渠,
请你画出修筑水渠的最短路线图.
分析 根据垂线段最短,分别过点A、B作河流的垂线段即可.
解析 如图所示,线段AE、BF就是
所求作的村庄A、村庄B修筑水渠的
最短路线.
题型四 利用方程解决角的互余与互补问题
例4 一个角的余角比这个角小20°,则这个角的补角为多少度?
题型四 利用方程解决角的互余与互补问题
例4 一个角的余角比这个角小20°,则这个角的补角为多少度?
解析 设这个角的度数为x度,
则x-(90-x)=20,解得x=55,
即这个角的度数为55°,
所以这个角的补角为180°-55°=125°.
1 两条直线的位置关系
知识点一 两条直线的位置关系
两条直线的位置关系
相交
平行
图示
注意
知识点一 两条直线的位置关系
两条直线的位置关系
相交
平行
两条直线只有一个公共点,我们称这两条直线为相交线
在同一平面内,不相交的两条直线叫做平行线
图示
注意
(1)两条直线平行必须具备三个条件:①在同一平面内;②不相交;③都是直线;(2)线段或射线平行是指线段或射线所在的直线互相平行
例1 下列说法正确的是( )
A.同一平面内没有公共点的两条线段平行
B.两条不相交的直线是平行线
C.同一平面内没有公共点的两条直线平行
D.同一平面内没有公共点的两条射线平行
例1 下列说法正确的是( )
A.同一平面内没有公共点的两条线段平行
B.两条不相交的直线是平行线
C.同一平面内没有公共点的两条直线平行
D.同一平面内没有公共点的两条射线平行
解析 两条线段虽然没有交点,但它们所在的直线可能有交点,A错误.若两条不相交的直线在不同的平面内,则这两条直线也不是平行线,B错误.选项C符合两直线平行的三个条件:①是直线;②在同一平面内;③没有交点两条射线虽然没有交点,但它们所在的直线可能有交点,D错误.
例1 下列说法正确的是( )
A.同一平面内没有公共点的两条线段平行
B.两条不相交的直线是平行线
C.同一平面内没有公共点的两条直线平行
D.同一平面内没有公共点的两条射线平行
解析 两条线段虽然没有交点,但它们所在的直线可能有交点,A错误.若两条不相交的直线在不同的平面内,则这两条直线也不是平行线,B错误.选项C符合两直线平行的三个条件:①是直线;②在同一平面内;③没有交点两条射线虽然没有交点,但它们所在的直线可能有交点,D错误.
答案 C
知识点二 对顶角及其性质
定义
性质
图例
对顶角
拓展延伸
温馨提示
知识点二 对顶角及其性质
定义
性质
图例
对顶角
有一个公共顶点,并且一个角的两边分别是另一个角两边的反向延长线.具有这种位置关系的两个角互为对顶角
对顶角相等.如图,
∠1=∠3,∠2=∠4
拓展延伸
(1)两条直线相交形成两对对顶角.(2)判断两个角是不是对顶角,应抓住两点:一是两个角是否有公共顶点,二是两角的两边是否分别互为反向延长线
温馨提示
对顶角相等,但相等的角不一定是对顶角
例2 下列四个图中,∠1与∠2是对顶角的是( )
例2 下列四个图中,∠1与∠2是对顶角的是( )
解析 两个角是对顶角,则两角的两边必须互为反向延长线,故A,D错误;两个角是对顶角,则两角必须有公共顶点,故B错误,C正确.
例2 下列四个图中,∠1与∠2是对顶角的是( )
解析 两个角是对顶角,则两角的两边必须互为反向延长线,故A,D错误;两个角是对顶角,则两角必须有公共顶点,故B错误,C正确.
答案 C
知识点三 互余、互补及其性质
互补
互余
定义
性质
注意
知识点三 互余、互补及其性质
互补
互余
定义
两个角的和是180°
两个角的和是90°
性质
同角或等角的补角相等
同角或等角的余角相等
注意
(1)互余、互补是指两个角之间的数量关系,与两个角的位置无关.
(2)互余的两个角都是锐角,而互补的两个角可能一个是锐角、一个是钝角,也可能都是直角
例3 如图所示,O是直线AB上一点,∠AOC=∠BOC=∠DOE=90°.
(1)图中互为余角的角有几对?各是哪些?
(2)∠1的余角是哪些?
(3)图中互为补角的角有几对?各是哪些?
(4)∠1的补角是哪个?
解析 (1)互为余角的角有4对,分别是∠1与∠2,∠3与∠4,∠2与∠3,∠1与∠4.
(2)由∠1+∠2=90°,∠1+∠4=90°得,∠1的余角是∠2和∠4.
(3)互为补角的角有7对,分别是∠1与∠BOD,∠AOC与∠BOC,∠4与∠AOE,∠3与∠BOD,∠2与∠AOE,∠DOE与∠AOC,∠DOE与∠BOC.
(4)由∠1+∠BOD=180°得,∠1的补角是∠BOD.
知识点四 垂直及垂线的画法
1.垂直的相关定义
定义
符号语言
图例
垂直
拓展延伸
知识点四 垂直及垂线的画法
1.垂直的相关定义
定义
符号语言
图例
垂直
两条直线相交所成的四个角中有一个角为90°时,这两条直线互相垂直其中一条直线是另一条直线的垂线,它们的交点叫垂足
如图,∠AOC=90°或∠BOC=90°或∠AOD=90°或∠BOD=90° AB⊥CD
拓展延伸
(1)垂直是两条直线相交的特殊情况,特殊在夹角为90°.(2)垂直的定义具有双重作用,即已知夹角为直角可以得到两直线垂直(判定);由两直线垂直可以得到夹角为90°(性质)
2.垂线的画法
画垂线
的方法
温馨提示
2.垂线的画法
画垂线的方法
用三角尺画垂线
“一靠、二过、三画”,即第一步:把三角尺的一条直角边靠在已知直线上;第二步:使三角尺的另一条直角边经过已知点;第三步:沿已知点所在的直角边画出直线
用直尺画垂线、用量角器画垂线、用折纸的方法折出垂线
温馨提示
(1)过一点画射线或线段的垂线,是指画它们所在直线的垂线,垂足可能在射线的反向延长线或线段的延长线上.(2)画垂线时是实线,如需延长线段或反向延长射线,则用虚线
例4 已知:如图所示,直线AB,CD相交于点O,OE⊥CD于点O,∠BOD=40°.求∠AOE的度数.
例4 已知:如图所示,直线AB,CD相交于点O,OE⊥CD于点O,∠BOD=40°.求∠AOE的度数.
解析 因为OE⊥CD,
所以∠DOE=90°,
因为∠BOD=40°,
所以∠AOE=180°-90°-40°=50°.
知识点五 垂线段及性质
1.垂线段
定义
图形
识记
垂
线
段
拓展延伸
知识点五 垂线段及性质
1.垂线段
定义
图形
识记
垂
线
段
连接直线 外一点A与直线 上各点的线段中,与直线 垂直的线段叫做点A到直线 的垂线段
线段AO是直线的垂线段.
线段AO的长度叫做点A到直线
的距离
拓展延伸
(1)垂线是直线,垂线段是线段
(2)斜线段有无数条,但垂线段只有一条
2.性质
性质一
性质二
内容
拓展延伸
2.性质
性质一
性质二
内容
在同一平面内,过一点有且只有一条直线与已知直线垂直
直线外一点与直线上各点连接的所有线段中,垂线段最短
拓展延伸
(1)有且只有“说明了垂线的存在性和唯一性.(2)“过一点”中的这一点,可以在已知直线上,也可以在已知直线外
(1)垂线段是一条线段,它是有长度的.(2)“一点”必须在直线外,若这点在直线上,就构不成垂线段,故这一点不能在直线上
例5 下列图形中,线段PQ的长表示点P到直线MN的距离的是( )
例5 下列图形中,线段PQ的长表示点P到直线MN的距离的是( )
解析 根据点到直线的距离的概念可知,线段PQ的长表示点P到直线MN的距离的是A.
例5 下列图形中,线段PQ的长表示点P到直线MN的距离的是( )
解析 根据点到直线的距离的概念可知,线段PQ的长表示点P到直线MN的距离的是A.
答案 A
经典例题
题型一 与对顶角有关的计算
例1 如图所示,三条直线 AB CDEF交于点O,已知∠3=3∠2、∠2=2∠1,求∠1、∠2、∠3的大小.
题型一 与对顶角有关的计算
例1 如图所示,三条直线 AB CDEF交于点O,已知∠3=3∠2、∠2=2∠1,求∠1、∠2、∠3的大小.
分析 根据∠2=∠FOD,∠1+∠FOD+∠3=180°,建立等量系求解.
题型一 与对顶角有关的计算
例1 如图所示,三条直线 AB CDEF交于点O,已知∠3=3∠2、∠2=2∠1,求∠1、∠2、∠3的大小.
分析 根据∠2=∠FOD,∠1+∠FOD+∠3=180°,建立等量系求解.
解析 设∠1=x°,则∠2=2∠1=2x°,∴∠3=3∠2=6x°,因为∠2=∠FOD,∠1+∠FOD+∠3=180°,所以x+2x+6x=180,解得x=20,∴∠1=20°,∠2=40°,∠3=120°.
题型一 与对顶角有关的计算
例1 如图所示,三条直线 AB CDEF交于点O,已知∠3=3∠2、∠2=2∠1,求∠1、∠2、∠3的大小.
分析 根据∠2=∠FOD,∠1+∠FOD+∠3=180°,建立等量系求解.
解析 设∠1=x°,则∠2=2∠1=2x°,∴∠3=3∠2=6x°,因为∠2=∠FOD,∠1+∠FOD+∠3=180°,所以x+2x+6x=180,解得x=20,∴∠1=20°,∠2=40°,∠3=120°.
点拨 本题的隐含条件是平角等于180度.当题目中没有角的具体度数,却需要求某些角的度数时,往往借助隐含条件解决问题.
题型二 与互余或互补有关的计算
例2 如图所示,∠AOB与∠BOD互为余角,OB是∠AOC的平分线,∠AOB=25°,求∠CODB的度数.
题型二 与互余或互补有关的计算
例2 如图所示,∠AOB与∠BOD互为余角,OB是∠AOC的平分线,∠AOB=25°,求∠CODB的度数.
解析 因为OB是∠AOC的平分线,∠AOB=25°,所以∠BOC=∠AOB=25°,因为∠AOB与∠BOD互为余角,所以∠BOD=90°-∠AOB=90°-25°=65°,所以∠COD=∠BOD-∠BOC=65°-25°=40°.
题型三 垂线段性质的运用
例3 如图所示,村庄A、村庄B分别要
从河流L引水入庄,各需修筑一条水渠,
请你画出修筑水渠的最短路线图.
题型三 垂线段性质的运用
例3 如图所示,村庄A、村庄B分别要
从河流L引水入庄,各需修筑一条水渠,
请你画出修筑水渠的最短路线图.
分析 根据垂线段最短,分别过点A、B作河流的垂线段即可.
题型三 垂线段性质的运用
例3 如图所示,村庄A、村庄B分别要
从河流L引水入庄,各需修筑一条水渠,
请你画出修筑水渠的最短路线图.
分析 根据垂线段最短,分别过点A、B作河流的垂线段即可.
解析 如图所示,线段AE、BF就是
所求作的村庄A、村庄B修筑水渠的
最短路线.
题型四 利用方程解决角的互余与互补问题
例4 一个角的余角比这个角小20°,则这个角的补角为多少度?
题型四 利用方程解决角的互余与互补问题
例4 一个角的余角比这个角小20°,则这个角的补角为多少度?
解析 设这个角的度数为x度,
则x-(90-x)=20,解得x=55,
即这个角的度数为55°,
所以这个角的补角为180°-55°=125°.
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
