2020-2021学年七年级数学北师大版下册《2.3平行线的性质》同步训练(word版含答案)
文档属性
| 名称 | 2020-2021学年七年级数学北师大版下册《2.3平行线的性质》同步训练(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 239.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-12 00:00:00 | ||
图片预览

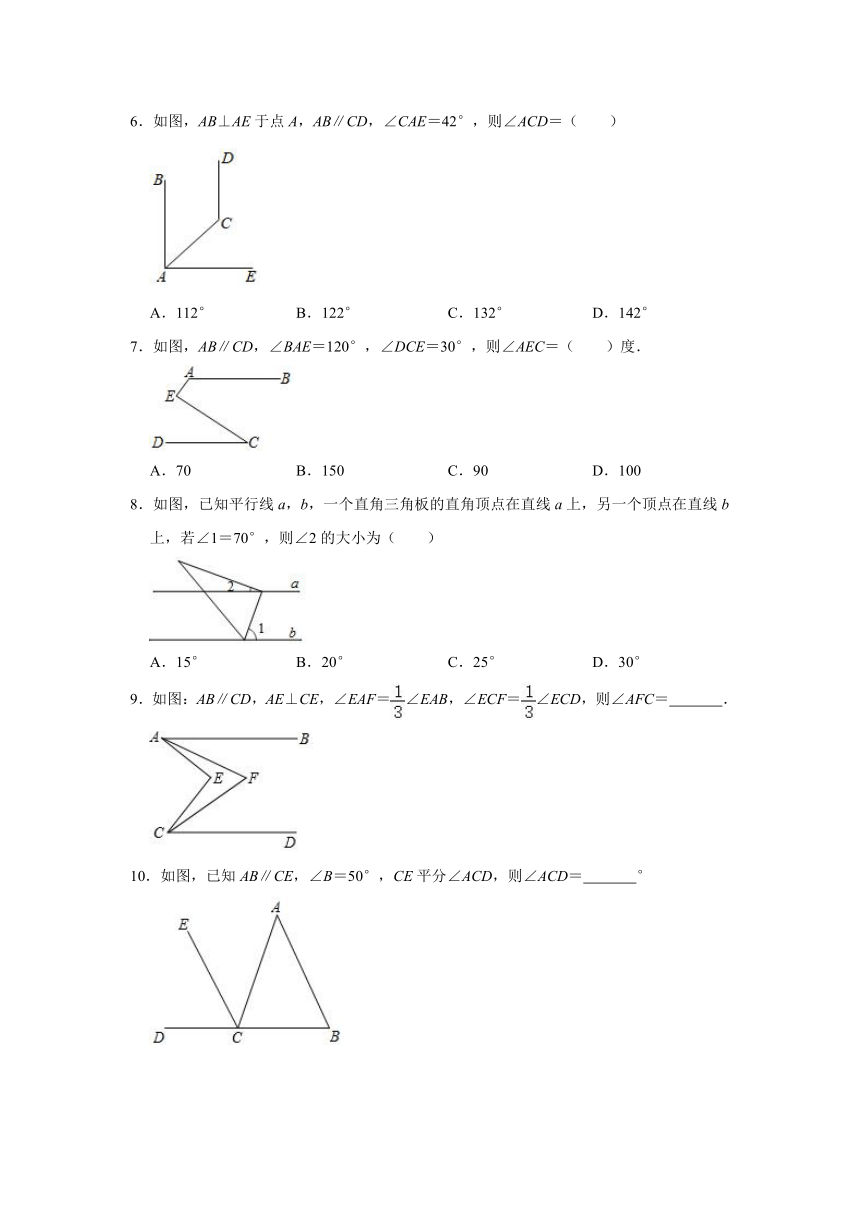


文档简介
2020-2021年度北师大版七年级数学下册《2.3平行线的性质》同步训练(附答案)
1.“折叠”是数学上常见构造新图形的重要方法如图,长方形ABCD中,点E在边AB上,将长方形形ABCD沿图中标示的DE折叠,点A恰好落在边BC的点G处,若∠CDG=52°,则∠DEG的度数为( )
A.73° B.71° C.68° D.52°
2.如图,直线AB∥CD,∠B=50°,∠D=20°,则∠E的度数是( )
A.20° B.30° C.50° D.70°
3.如图,AB∥EF,∠C=90°,则α、β、γ的关系为( )
A.β=α+γ B.α+β﹣γ=90° C.α+β+γ=180° D.β+γ﹣α=90°
4.如图,直线AB∥CD,AE⊥CE,∠1=125°,则∠C等于( )
A.35° B.45° C.50° D.55°
5.如图,直线AB∥CD∥EF,点O在直线EF上,下列结论正确的是( )
A.∠α+∠β﹣∠γ=90° B.∠α+∠γ﹣∠β=180°
C.∠γ+∠β﹣∠α=180° D.∠α+∠β+∠γ=180°
6.如图,AB⊥AE于点A,AB∥CD,∠CAE=42°,则∠ACD=( )
A.112° B.122° C.132° D.142°
7.如图,AB∥CD,∠BAE=120°,∠DCE=30°,则∠AEC=( )度.
A.70 B.150 C.90 D.100
8.如图,已知平行线a,b,一个直角三角板的直角顶点在直线a上,另一个顶点在直线b上,若∠1=70°,则∠2的大小为( )
A.15° B.20° C.25° D.30°
9.如图:AB∥CD,AE⊥CE,∠EAF=∠EAB,∠ECF=∠ECD,则∠AFC= .
10.如图,已知AB∥CE,∠B=50°,CE平分∠ACD,则∠ACD= °
11.如图①是长方形纸带,∠DEF=α,将纸带沿EF折叠成图②,再沿BF折叠成图③,则图③中的∠CFE的度数是 .
12.如图,AB∥CD,点M为CD上一点,MF平分∠CME.若∠1=57°,则∠EMD的大小为 度.
13.如图,已知AB∥CD,AD平分∠BAC,∠1=70°,则∠ADC的度数是 .
14.在同一平面内,∠A与∠B的两边分别平行,若∠A=50°,则∠B的度数为 °.
15.∠AOB=40°,BC∥OA,过点C作直线OA的垂线,点D为垂足,若∠OCD=2∠OCB,则∠COB为 度.
16.如图,已知AE∥BD,∠1=130°,∠2=30°,则∠C= .
17.如图,已知直线AB∥CD,∠GEB的平分线EF交CD于点F,∠1=40°,则∠2等于 .
18.将一副直角三角板按如图所示的方式放置在两平行线(l1∥l2)之间,则图中的∠1= .
19.将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°).
(1)如图1,①若∠DCE=40°,求∠ACB的度数;
②若∠ACB=150°,直接写出∠DCE的度数是 度.
(2)由(1)猜想∠ACB与∠DCE满足的数量关系是 .
(3)若固定△ACD,将△BCE绕点C旋转,
①当旋转至BE∥AC(如图2)时,直接写出∠ACE的度数是 度.
②继续旋转至BC∥DA(如图3)时,求∠ACE的度数.
20.如图①,直线l1∥l2,直线EF和直线l1、l2分别交于C、D两点,点A、B分别在直线l1、l2上,点P在直线EF上,连结PA、PB.
猜想:如图①,若点P在线段CD上,∠PAC=15°,∠PBD=40°,则∠APB的大小为 度.
探究:如图①,若点P在线段CD上,直接写出∠PAC、∠APB、∠PBD之间的数量关系.
拓展:如图②,若点P在射线CE上或在射线DF上时,直接写出∠PAC、∠APB、∠PBD之间的数量关系.
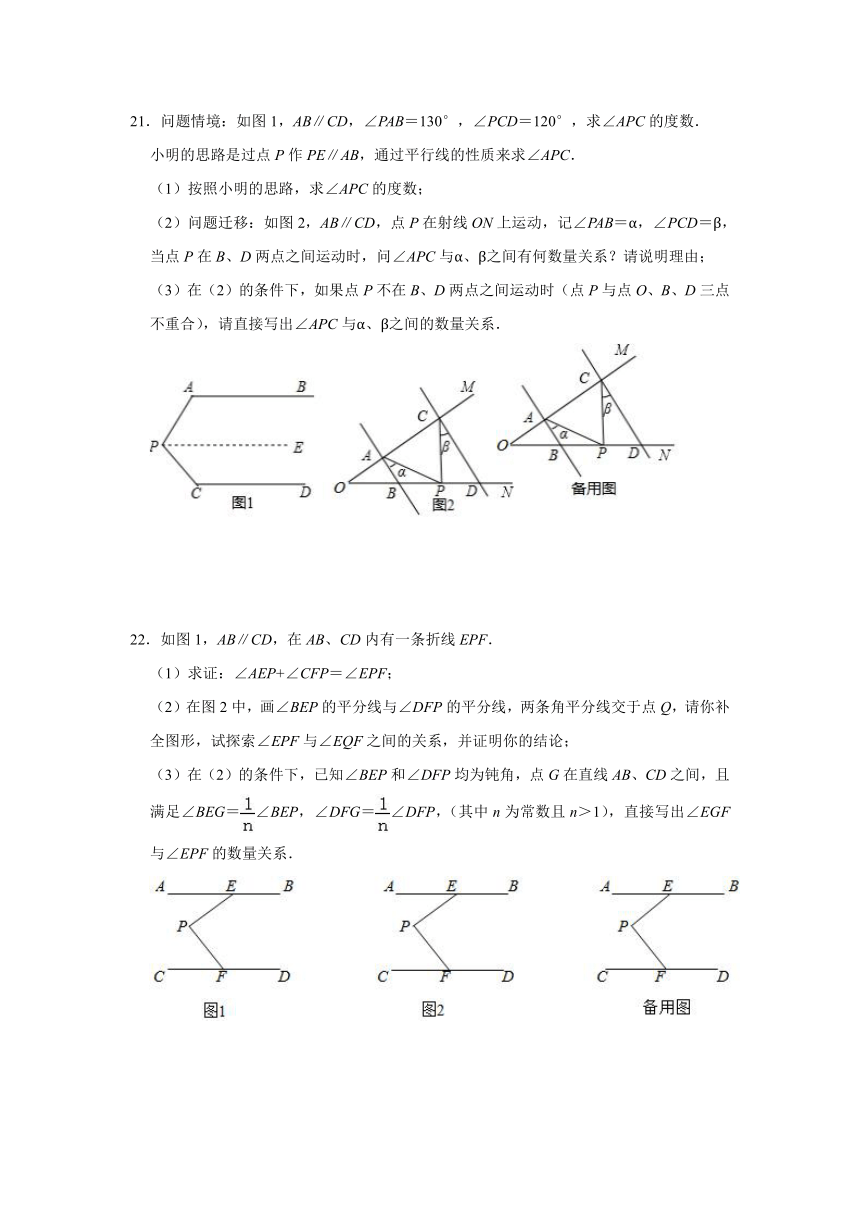
21.问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是过点P作PE∥AB,通过平行线的性质来求∠APC.
(1)按照小明的思路,求∠APC的度数;
(2)问题迁移:如图2,AB∥CD,点P在射线ON上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点P不在B、D两点之间运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.
22.如图1,AB∥CD,在AB、CD内有一条折线EPF.
(1)求证:∠AEP+∠CFP=∠EPF;
(2)在图2中,画∠BEP的平分线与∠DFP的平分线,两条角平分线交于点Q,请你补全图形,试探索∠EPF与∠EQF之间的关系,并证明你的结论;
(3)在(2)的条件下,已知∠BEP和∠DFP均为钝角,点G在直线AB、CD之间,且满足∠BEG=∠BEP,∠DFG=∠DFP,(其中n为常数且n>1),直接写出∠EGF与∠EPF的数量关系.
23.已知,直线AB∥CD,∠EFG=90°.
(1)如图1,点F在AB上,FG与CD交于点N,若∠EFB=65°,则∠FNC= °;
(2)如图2,点F在AB与CD之间,EF与AB交于点M,FG与CD交于点N.∠AMF的平分线MH与∠CNF的平分线NH交于点H.
①若∠EMB=α,求∠FNC(用含α的式子表示);
②求∠MHN的度数.
参考答案
1.解:∵∠CDG=52°,
∴∠ADG=90°﹣∠CDG=90°﹣52°=38°,
又∵∠ADE=∠GDE===19°,∠DAE=∠DGE=90°,
∴∠DEG=90°﹣∠GDE=90°﹣19°=71°.
故选:B.
2.解:∵AB∥CD,
∴∠BMD=∠B=50°,
又∵∠BMD是△CDE的外角,
∴∠E=∠BMD﹣∠D=50°﹣20°=30°.
故选:B.
3.解:延长DC交AB与G,延长CD交EF于H.
直角△BGC中,∠1=90°﹣α;
△EHD中,∠2=β﹣γ,
∵AB∥EF,
∴∠1=∠2,
∴90°﹣α=β﹣γ,
即α+β﹣γ=90°.
故选:B.
4.解:过点E作EF∥AB,则EF∥CD,如图所示.
∵EF∥AB,
∴∠BAE=∠AEF.
∵EF∥CD,
∴∠C=∠CEF.
∵AE⊥CE,
∴∠AEC=90°,即∠AEF+∠CEF=90°,
∴∠BAE+∠C=90°.
∵∠1=125°,∠1+∠BAE=180°,
∴∠BAE=180°﹣125°=55°,
∴∠C=90°﹣55°=35°.
故选:A.
5.解:∵AB∥EF,
∴∠α=∠BOF,
∵CD∥EF,
∴∠γ+∠COF=180°,
∵∠BOF=∠COF+∠β,
∴∠γ+∠α﹣∠β=180°,
故选:B.
6.解:∵AB⊥AE,∠CAE=42°,
∴∠BAC=90°﹣42°=48°,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠ACD=132°.
故选:C.
7.解:如图,延长AE交CD于点F,
∵AB∥CD,
∴∠BAE+∠EFC=180°,
又∵∠BAE=120°,
∴∠EFC=180°﹣∠BAE=180°﹣120°=60°,
又∵∠DCE=30°,
∴∠AEC=∠DCE+∠EFC=30°+60°=90°.
故选:C.
8.解:∵a∥b,∠1=70°
∴∠3=70°,
∵直角三角板的直角顶点在直线a上,
∴∠2=90°﹣∠3=20°,
故选:B.
9.解:连接AC,设∠EAF=x,∠ECF=y,∠EAB=3x,∠ECD=3y,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠CAE+3x+∠ACE+3y=180°,
∴∠CAE+∠ACE=180°﹣(3x+3y),∠FAC+∠FCA=180°﹣(2x+2y)
∴∠AEC=180°﹣(∠CAE+∠ACE)
=180°﹣[180°﹣(3x+3y)]=3x+3y=3(x+y),
∠AFC=180°﹣(∠FAC+∠FCA)
=180°﹣[180°﹣(2x+2y)]=2x+2y=2(x+y),
∵AE⊥CE,
∴∠AEC=90°,
∴∠AFC=∠AEC=×90°=60°.
故答案为:60°.
10.解:∵AB∥CE,∠B=50°,
∴∠ECD=∠B=50°,
∵CE平分∠ACD,
∴∠ACD=2∠ECD=2×50°=100°,
故答案为:100.
11.解:∵AD∥BC,
∴∠BFE=∠DEF=α,∠CFE=180°﹣∠DEF=180°﹣α,
∴∠CFG=∠CFE﹣∠BFE=180°﹣α﹣α=180°﹣2α,
∴∠CFE=∠CFG﹣∠BFE=180°﹣2α﹣α=180°﹣3α.
故答案为:180°﹣3α.
12.解:∵AB∥CD,
∴∠CMF=∠1=57°,
∵MF平分∠CME,
∴∠CME=2∠CMF=114°.
又∵∠CME+∠EMD=180°,
∴∠EMD=180°﹣∠CME=180°﹣114°=66°.
故答案为:66.
13.解:∵AB∥CD,
∴∠1+∠BAC=180°,
∴∠BAC=180°﹣∠1=180°﹣70°=110°.
∵AD平分∠BAC,
∴∠BAD=∠BAC=×110°=55°.
∵AB∥CD,
∴∠ADC=∠BAD=55°.
故答案为:55°.
14.解:∵∠A与∠B的两边分别平行,
∴∠A=∠B或∠A+∠B=180°,
∵∠A=50°,
∴∠B=50°,或∠B=180°﹣∠A=180°﹣50°=130°.
故答案为:50或130.
15.解:如图所示,当点D在AO上时,
∵BC∥OA,CD⊥AO,
∴∠BCD=90°,
又∵∠OCD=2∠OCB,
∴∠BCO=30°=∠AOC,
又∵∠AOB=40°,
∴∠COB=40°﹣30°=10°;
如图所示,当点D在AO的延长线上时,
∵BC∥OA,CD⊥AO,
∴∠BCD=90°,
又∵∠OCD=2∠OCB,
∴∠BCO=30°=∠DOC,
又∵∠AOB=40°,
∴∠COB=180°﹣40°﹣30°=110°;
故答案为:10或110.
16.解:∵AE∥BD,∠1=130°,∠2=30°,
∴∠CBD=∠1=130°.
∵∠BDC=∠2,
∴∠BDC=30°.
在△BCD中,∠CBD=130°,∠BDC=30°,
∴∠C=180°﹣130°﹣30°=20°.
故答案为:20°.
17.解:∵AB∥CD,
∴∠BEG=∠1=40°,
∵EF是∠GEB的平分线,
∴∠BEF=∠BEG=×40°=20°,
∵AB∥CD,
∴∠2=180°﹣∠BEF=180°﹣20°=160°.
故答案为:160°.
18.解:延长BC交直线l1于A,
∵l1∥l2,且∠ABE=60°,
∴∠BAD=180°﹣60°=120°,
∵∠BCE=90°,∠DCE=45°,
∴∠ACD=180°﹣90°﹣45°=45°,
∴∠1=180°﹣∠BAD﹣∠ACD=180°﹣45°﹣120°=15°.
故答案为:15°.
19.解:(1)
①∵∠DCE=40°,
∴∠ACE=∠ACD﹣∠DCE=50°,
∴∠ACB=∠ACE+∠ECB=50°+90°=140°;
②∵∠ACB=150°,∠ACD=90°,
∴∠ACE=150°﹣90°=60°,
∴∠DCE=∠ACD﹣∠ACE=90°﹣60°=30°,
故答案为:30;
(2)∵∠ACB=∠ACD+∠BCE﹣∠DCE=90°+90°﹣∠DCE,
∴∠ACB+∠DCE=180°,
故答案为:∠ACB+∠DCE=180°;
(3)①∵BE∥AC,
∴∠ACE=∠E=45°,
故答案为:45°;
②∵BC∥DA,
∴∠A+∠ACB=180°,
又∵∠A=60°,
∴∠ACB=180°﹣60°=120°,
∵∠BCE=90°,
∴∠BCD=∠ACB﹣∠ECB=120°﹣90°=30°.
20.解:猜想:如图①,过点P作PG∥l1,
∵l1∥l2,
∴l1∥l2∥PG,
∴∠APG=∠PAC=15°,∠BPG=∠PBD=40°,
∴∠APB=∠APG+∠BPG=∠PAC+∠PBD=15°+40°=55°,
∴∠APB的大小为55度,
故答案为:55;
探究:如图①,∠PAC=∠APB﹣∠PBD,理由如下:
∵l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠APB=∠APG+∠BPG=∠PAC+∠PBD,
∴∠PAC=∠APB﹣∠PBD;
拓展:∠PAC=∠PBD﹣∠APB或∠PAC=∠APB+∠PBD,理由如下:
如图,当点P在射线CE上时,
过点P作PG∥l1,
∴l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠PAC=∠APG=∠BPG﹣∠APB,
∴∠PAC=∠PBD﹣∠APB;
当点P在射线DF上时,
过点P作PG∥l1,
∴l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠PAC=∠APG=∠APB+∠BPG,
∴∠PAC=∠APB+∠PBD,
综上所述:当点P在射线CE上或在射线DF上时,∠PAC=∠PBD﹣∠APB或∠PAC=∠APB+∠PBD.
21.(1)解:过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°,
∴∠APC=∠APE+∠CPE=110°.
(2)∠APC=∠α+∠β,
理由:如图2,过P作PE∥AB交AC于E,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠α=∠APE,∠β=∠CPE,
∴∠APC=∠APE+∠CPE=∠α+∠β;
(3)如图所示,当P在BD延长线上时,
∠CPA=∠α﹣∠β;
如图所示,当P在DB延长线上时,
∠CPA=∠β﹣∠α.
22.证明:(1)如图1,过点P作PG∥AB,
,
∵AB∥CD,
∴PG∥CD,
∴∠AEP=∠1,∠CFP=∠2,
又∵∠1+∠2=∠EPF,
∴∠AEP+∠CFP=∠EPF;
(2)如图2,
,
由(1)可得:∠EPF=∠AEP+CFP,∠EQF=∠BEQ+∠DFQ,
∵∠BEP的平分线与∠DFP的平分线相交于点Q,
∴∠EQF=∠BEQ+∠DFQ=(∠BEP+∠DFP)=[360°﹣(∠AEP+∠CFP)]=(360﹣∠EPF),
∴∠EPF+2∠EQF=360°;
(3)由(1)可得:
∠EGF=∠AEG+∠CFG,∠EPF=∠BEP+∠DFP,
∵∠BEP=∠BEG,∠DFP=∠DFG,
∴∠EPF=∠BEP+∠DFP=(∠BEG+∠DFG)=[360°﹣(∠AEG+∠CFG)]=×(360°﹣∠EGF),
∴∠EGF+n∠EPF=360°.
23.解:(1)∵∠EFG=90°,∠EFB=65°,
∴∠BFD=90°﹣65°=25°,
∵AB∥CD,
∴∠FNC=∠BFD=25°,
故答案为:25;
(2)①如图1,过F作FP∥AB,连接EG,
∵AB∥CD,
∴AB∥CD∥FP,
∴∠MFP=∠EMB=α,
又∵∠EFG=90°,
∴∠PFN=90°﹣α,
∵FP∥CD,
∴∠FNC=∠PFN=90°﹣α;
②如图2,过F作FQ∥AB,
∵AB∥CD,
∴AB∥CD∥FQ,
∴∠MFQ=∠AMF,∠QFN=∠CNF,
∴∠AMF+∠CNF=∠MFQ+∠QFN=∠EFG=90°,
过H作HR∥AB,
∵AB∥CD,
∴AB∥CD∥HR,
∴∠AMH=∠MHR,∠HNC=∠NHR,
又∵MH平分∠AMF,NH平分∠CNF,
∴∠AMH=∠AMF,∠HNC=∠CNF,
∴∠MHN=∠MHR+∠NHR=∠AMH+∠HNC=(∠AMF+∠CNF)=×90°=45°
1.“折叠”是数学上常见构造新图形的重要方法如图,长方形ABCD中,点E在边AB上,将长方形形ABCD沿图中标示的DE折叠,点A恰好落在边BC的点G处,若∠CDG=52°,则∠DEG的度数为( )
A.73° B.71° C.68° D.52°
2.如图,直线AB∥CD,∠B=50°,∠D=20°,则∠E的度数是( )
A.20° B.30° C.50° D.70°
3.如图,AB∥EF,∠C=90°,则α、β、γ的关系为( )
A.β=α+γ B.α+β﹣γ=90° C.α+β+γ=180° D.β+γ﹣α=90°
4.如图,直线AB∥CD,AE⊥CE,∠1=125°,则∠C等于( )
A.35° B.45° C.50° D.55°
5.如图,直线AB∥CD∥EF,点O在直线EF上,下列结论正确的是( )
A.∠α+∠β﹣∠γ=90° B.∠α+∠γ﹣∠β=180°
C.∠γ+∠β﹣∠α=180° D.∠α+∠β+∠γ=180°
6.如图,AB⊥AE于点A,AB∥CD,∠CAE=42°,则∠ACD=( )
A.112° B.122° C.132° D.142°
7.如图,AB∥CD,∠BAE=120°,∠DCE=30°,则∠AEC=( )度.
A.70 B.150 C.90 D.100
8.如图,已知平行线a,b,一个直角三角板的直角顶点在直线a上,另一个顶点在直线b上,若∠1=70°,则∠2的大小为( )
A.15° B.20° C.25° D.30°
9.如图:AB∥CD,AE⊥CE,∠EAF=∠EAB,∠ECF=∠ECD,则∠AFC= .
10.如图,已知AB∥CE,∠B=50°,CE平分∠ACD,则∠ACD= °
11.如图①是长方形纸带,∠DEF=α,将纸带沿EF折叠成图②,再沿BF折叠成图③,则图③中的∠CFE的度数是 .
12.如图,AB∥CD,点M为CD上一点,MF平分∠CME.若∠1=57°,则∠EMD的大小为 度.
13.如图,已知AB∥CD,AD平分∠BAC,∠1=70°,则∠ADC的度数是 .
14.在同一平面内,∠A与∠B的两边分别平行,若∠A=50°,则∠B的度数为 °.
15.∠AOB=40°,BC∥OA,过点C作直线OA的垂线,点D为垂足,若∠OCD=2∠OCB,则∠COB为 度.
16.如图,已知AE∥BD,∠1=130°,∠2=30°,则∠C= .
17.如图,已知直线AB∥CD,∠GEB的平分线EF交CD于点F,∠1=40°,则∠2等于 .
18.将一副直角三角板按如图所示的方式放置在两平行线(l1∥l2)之间,则图中的∠1= .
19.将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°).
(1)如图1,①若∠DCE=40°,求∠ACB的度数;
②若∠ACB=150°,直接写出∠DCE的度数是 度.
(2)由(1)猜想∠ACB与∠DCE满足的数量关系是 .
(3)若固定△ACD,将△BCE绕点C旋转,
①当旋转至BE∥AC(如图2)时,直接写出∠ACE的度数是 度.
②继续旋转至BC∥DA(如图3)时,求∠ACE的度数.
20.如图①,直线l1∥l2,直线EF和直线l1、l2分别交于C、D两点,点A、B分别在直线l1、l2上,点P在直线EF上,连结PA、PB.
猜想:如图①,若点P在线段CD上,∠PAC=15°,∠PBD=40°,则∠APB的大小为 度.
探究:如图①,若点P在线段CD上,直接写出∠PAC、∠APB、∠PBD之间的数量关系.
拓展:如图②,若点P在射线CE上或在射线DF上时,直接写出∠PAC、∠APB、∠PBD之间的数量关系.
21.问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是过点P作PE∥AB,通过平行线的性质来求∠APC.
(1)按照小明的思路,求∠APC的度数;
(2)问题迁移:如图2,AB∥CD,点P在射线ON上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点P不在B、D两点之间运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.
22.如图1,AB∥CD,在AB、CD内有一条折线EPF.
(1)求证:∠AEP+∠CFP=∠EPF;
(2)在图2中,画∠BEP的平分线与∠DFP的平分线,两条角平分线交于点Q,请你补全图形,试探索∠EPF与∠EQF之间的关系,并证明你的结论;
(3)在(2)的条件下,已知∠BEP和∠DFP均为钝角,点G在直线AB、CD之间,且满足∠BEG=∠BEP,∠DFG=∠DFP,(其中n为常数且n>1),直接写出∠EGF与∠EPF的数量关系.
23.已知,直线AB∥CD,∠EFG=90°.
(1)如图1,点F在AB上,FG与CD交于点N,若∠EFB=65°,则∠FNC= °;
(2)如图2,点F在AB与CD之间,EF与AB交于点M,FG与CD交于点N.∠AMF的平分线MH与∠CNF的平分线NH交于点H.
①若∠EMB=α,求∠FNC(用含α的式子表示);
②求∠MHN的度数.
参考答案
1.解:∵∠CDG=52°,
∴∠ADG=90°﹣∠CDG=90°﹣52°=38°,
又∵∠ADE=∠GDE===19°,∠DAE=∠DGE=90°,
∴∠DEG=90°﹣∠GDE=90°﹣19°=71°.
故选:B.
2.解:∵AB∥CD,
∴∠BMD=∠B=50°,
又∵∠BMD是△CDE的外角,
∴∠E=∠BMD﹣∠D=50°﹣20°=30°.
故选:B.
3.解:延长DC交AB与G,延长CD交EF于H.
直角△BGC中,∠1=90°﹣α;
△EHD中,∠2=β﹣γ,
∵AB∥EF,
∴∠1=∠2,
∴90°﹣α=β﹣γ,
即α+β﹣γ=90°.
故选:B.
4.解:过点E作EF∥AB,则EF∥CD,如图所示.
∵EF∥AB,
∴∠BAE=∠AEF.
∵EF∥CD,
∴∠C=∠CEF.
∵AE⊥CE,
∴∠AEC=90°,即∠AEF+∠CEF=90°,
∴∠BAE+∠C=90°.
∵∠1=125°,∠1+∠BAE=180°,
∴∠BAE=180°﹣125°=55°,
∴∠C=90°﹣55°=35°.
故选:A.
5.解:∵AB∥EF,
∴∠α=∠BOF,
∵CD∥EF,
∴∠γ+∠COF=180°,
∵∠BOF=∠COF+∠β,
∴∠γ+∠α﹣∠β=180°,
故选:B.
6.解:∵AB⊥AE,∠CAE=42°,
∴∠BAC=90°﹣42°=48°,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠ACD=132°.
故选:C.
7.解:如图,延长AE交CD于点F,
∵AB∥CD,
∴∠BAE+∠EFC=180°,
又∵∠BAE=120°,
∴∠EFC=180°﹣∠BAE=180°﹣120°=60°,
又∵∠DCE=30°,
∴∠AEC=∠DCE+∠EFC=30°+60°=90°.
故选:C.
8.解:∵a∥b,∠1=70°
∴∠3=70°,
∵直角三角板的直角顶点在直线a上,
∴∠2=90°﹣∠3=20°,
故选:B.
9.解:连接AC,设∠EAF=x,∠ECF=y,∠EAB=3x,∠ECD=3y,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠CAE+3x+∠ACE+3y=180°,
∴∠CAE+∠ACE=180°﹣(3x+3y),∠FAC+∠FCA=180°﹣(2x+2y)
∴∠AEC=180°﹣(∠CAE+∠ACE)
=180°﹣[180°﹣(3x+3y)]=3x+3y=3(x+y),
∠AFC=180°﹣(∠FAC+∠FCA)
=180°﹣[180°﹣(2x+2y)]=2x+2y=2(x+y),
∵AE⊥CE,
∴∠AEC=90°,
∴∠AFC=∠AEC=×90°=60°.
故答案为:60°.
10.解:∵AB∥CE,∠B=50°,
∴∠ECD=∠B=50°,
∵CE平分∠ACD,
∴∠ACD=2∠ECD=2×50°=100°,
故答案为:100.
11.解:∵AD∥BC,
∴∠BFE=∠DEF=α,∠CFE=180°﹣∠DEF=180°﹣α,
∴∠CFG=∠CFE﹣∠BFE=180°﹣α﹣α=180°﹣2α,
∴∠CFE=∠CFG﹣∠BFE=180°﹣2α﹣α=180°﹣3α.
故答案为:180°﹣3α.
12.解:∵AB∥CD,
∴∠CMF=∠1=57°,
∵MF平分∠CME,
∴∠CME=2∠CMF=114°.
又∵∠CME+∠EMD=180°,
∴∠EMD=180°﹣∠CME=180°﹣114°=66°.
故答案为:66.
13.解:∵AB∥CD,
∴∠1+∠BAC=180°,
∴∠BAC=180°﹣∠1=180°﹣70°=110°.
∵AD平分∠BAC,
∴∠BAD=∠BAC=×110°=55°.
∵AB∥CD,
∴∠ADC=∠BAD=55°.
故答案为:55°.
14.解:∵∠A与∠B的两边分别平行,
∴∠A=∠B或∠A+∠B=180°,
∵∠A=50°,
∴∠B=50°,或∠B=180°﹣∠A=180°﹣50°=130°.
故答案为:50或130.
15.解:如图所示,当点D在AO上时,
∵BC∥OA,CD⊥AO,
∴∠BCD=90°,
又∵∠OCD=2∠OCB,
∴∠BCO=30°=∠AOC,
又∵∠AOB=40°,
∴∠COB=40°﹣30°=10°;
如图所示,当点D在AO的延长线上时,
∵BC∥OA,CD⊥AO,
∴∠BCD=90°,
又∵∠OCD=2∠OCB,
∴∠BCO=30°=∠DOC,
又∵∠AOB=40°,
∴∠COB=180°﹣40°﹣30°=110°;
故答案为:10或110.
16.解:∵AE∥BD,∠1=130°,∠2=30°,
∴∠CBD=∠1=130°.
∵∠BDC=∠2,
∴∠BDC=30°.
在△BCD中,∠CBD=130°,∠BDC=30°,
∴∠C=180°﹣130°﹣30°=20°.
故答案为:20°.
17.解:∵AB∥CD,
∴∠BEG=∠1=40°,
∵EF是∠GEB的平分线,
∴∠BEF=∠BEG=×40°=20°,
∵AB∥CD,
∴∠2=180°﹣∠BEF=180°﹣20°=160°.
故答案为:160°.
18.解:延长BC交直线l1于A,
∵l1∥l2,且∠ABE=60°,
∴∠BAD=180°﹣60°=120°,
∵∠BCE=90°,∠DCE=45°,
∴∠ACD=180°﹣90°﹣45°=45°,
∴∠1=180°﹣∠BAD﹣∠ACD=180°﹣45°﹣120°=15°.
故答案为:15°.
19.解:(1)
①∵∠DCE=40°,
∴∠ACE=∠ACD﹣∠DCE=50°,
∴∠ACB=∠ACE+∠ECB=50°+90°=140°;
②∵∠ACB=150°,∠ACD=90°,
∴∠ACE=150°﹣90°=60°,
∴∠DCE=∠ACD﹣∠ACE=90°﹣60°=30°,
故答案为:30;
(2)∵∠ACB=∠ACD+∠BCE﹣∠DCE=90°+90°﹣∠DCE,
∴∠ACB+∠DCE=180°,
故答案为:∠ACB+∠DCE=180°;
(3)①∵BE∥AC,
∴∠ACE=∠E=45°,
故答案为:45°;
②∵BC∥DA,
∴∠A+∠ACB=180°,
又∵∠A=60°,
∴∠ACB=180°﹣60°=120°,
∵∠BCE=90°,
∴∠BCD=∠ACB﹣∠ECB=120°﹣90°=30°.
20.解:猜想:如图①,过点P作PG∥l1,
∵l1∥l2,
∴l1∥l2∥PG,
∴∠APG=∠PAC=15°,∠BPG=∠PBD=40°,
∴∠APB=∠APG+∠BPG=∠PAC+∠PBD=15°+40°=55°,
∴∠APB的大小为55度,
故答案为:55;
探究:如图①,∠PAC=∠APB﹣∠PBD,理由如下:
∵l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠APB=∠APG+∠BPG=∠PAC+∠PBD,
∴∠PAC=∠APB﹣∠PBD;
拓展:∠PAC=∠PBD﹣∠APB或∠PAC=∠APB+∠PBD,理由如下:
如图,当点P在射线CE上时,
过点P作PG∥l1,
∴l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠PAC=∠APG=∠BPG﹣∠APB,
∴∠PAC=∠PBD﹣∠APB;
当点P在射线DF上时,
过点P作PG∥l1,
∴l1∥l2∥PG,
∴∠APG=∠PAC,∠BPG=∠PBD,
∴∠PAC=∠APG=∠APB+∠BPG,
∴∠PAC=∠APB+∠PBD,
综上所述:当点P在射线CE上或在射线DF上时,∠PAC=∠PBD﹣∠APB或∠PAC=∠APB+∠PBD.
21.(1)解:过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°,
∴∠APC=∠APE+∠CPE=110°.
(2)∠APC=∠α+∠β,
理由:如图2,过P作PE∥AB交AC于E,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠α=∠APE,∠β=∠CPE,
∴∠APC=∠APE+∠CPE=∠α+∠β;
(3)如图所示,当P在BD延长线上时,
∠CPA=∠α﹣∠β;
如图所示,当P在DB延长线上时,
∠CPA=∠β﹣∠α.
22.证明:(1)如图1,过点P作PG∥AB,
,
∵AB∥CD,
∴PG∥CD,
∴∠AEP=∠1,∠CFP=∠2,
又∵∠1+∠2=∠EPF,
∴∠AEP+∠CFP=∠EPF;
(2)如图2,
,
由(1)可得:∠EPF=∠AEP+CFP,∠EQF=∠BEQ+∠DFQ,
∵∠BEP的平分线与∠DFP的平分线相交于点Q,
∴∠EQF=∠BEQ+∠DFQ=(∠BEP+∠DFP)=[360°﹣(∠AEP+∠CFP)]=(360﹣∠EPF),
∴∠EPF+2∠EQF=360°;
(3)由(1)可得:
∠EGF=∠AEG+∠CFG,∠EPF=∠BEP+∠DFP,
∵∠BEP=∠BEG,∠DFP=∠DFG,
∴∠EPF=∠BEP+∠DFP=(∠BEG+∠DFG)=[360°﹣(∠AEG+∠CFG)]=×(360°﹣∠EGF),
∴∠EGF+n∠EPF=360°.
23.解:(1)∵∠EFG=90°,∠EFB=65°,
∴∠BFD=90°﹣65°=25°,
∵AB∥CD,
∴∠FNC=∠BFD=25°,
故答案为:25;
(2)①如图1,过F作FP∥AB,连接EG,
∵AB∥CD,
∴AB∥CD∥FP,
∴∠MFP=∠EMB=α,
又∵∠EFG=90°,
∴∠PFN=90°﹣α,
∵FP∥CD,
∴∠FNC=∠PFN=90°﹣α;
②如图2,过F作FQ∥AB,
∵AB∥CD,
∴AB∥CD∥FQ,
∴∠MFQ=∠AMF,∠QFN=∠CNF,
∴∠AMF+∠CNF=∠MFQ+∠QFN=∠EFG=90°,
过H作HR∥AB,
∵AB∥CD,
∴AB∥CD∥HR,
∴∠AMH=∠MHR,∠HNC=∠NHR,
又∵MH平分∠AMF,NH平分∠CNF,
∴∠AMH=∠AMF,∠HNC=∠CNF,
∴∠MHN=∠MHR+∠NHR=∠AMH+∠HNC=(∠AMF+∠CNF)=×90°=45°
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
