2020-2021学年人教版数学八年级下册第十七章 17.2.1 勾股定理的逆定理(共56张)
文档属性
| 名称 | 2020-2021学年人教版数学八年级下册第十七章 17.2.1 勾股定理的逆定理(共56张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-12 00:00:00 | ||
图片预览











文档简介
第十七章
17.2.1 勾股定理的逆定理
人教版数学八年级下册
学习目标
1.能利用勾股定理的逆定理判定一个三角形是否为直角三角形.
2.灵活运用勾股定理及其逆定理解决问题.
3.理解原命题、逆命题、逆定理的概念及关系.
导入新知
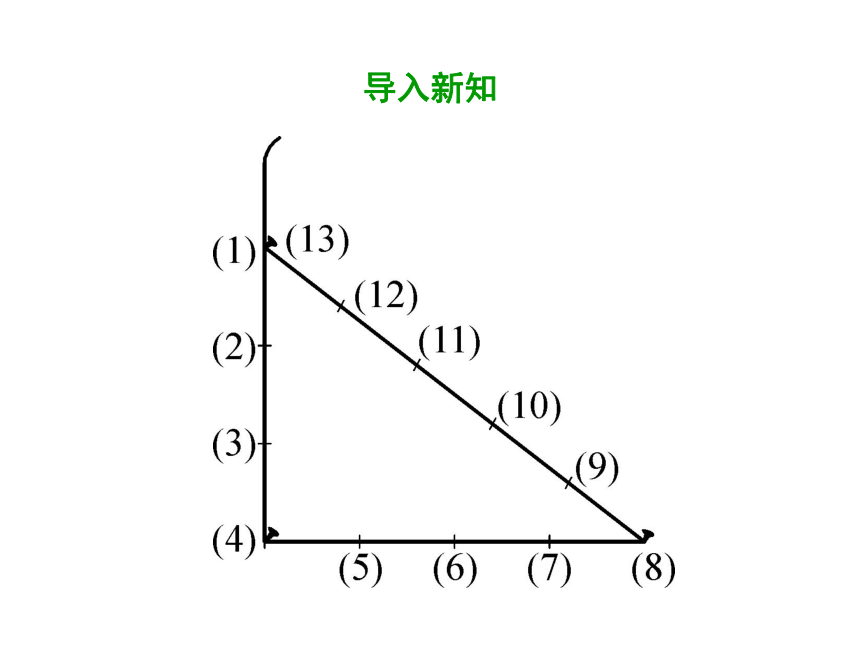
同学们,古埃及人曾经用下面的方法画直角:将一根长绳打上等距离的13个结,然后用桩钉成一个三角形(如图),他们认为其中一个角便是直角.你知道这是什么道理吗?
勾股定理的逆定理
1
知识点
逆命题、逆定理
如果两个命题的题设、结论正好相反,那么这
两个命题称为互逆命题,如果把其中一个叫做
原命题,那么另一个叫做它的逆命题.
合作探究
2.如果一个定理的逆命题经过证明是正确的,那
么它也是一个定理,称其为原定理的逆定理,
这两个定理称为互逆定理.
导引:根据题目要求,先判断原命题的真假,再将原命题
的题设和结论互换,写出原命题的逆命题,最后判
断逆命题的真假.
例1 判断下列命题的真假,写出逆命题,并判断逆命题
的真假:
(1)如果两条直线相交,那么它们只有一个交点;
(2)如果a>b,那么a2>b2;
(3)如果两个数互为相反数,那么它们的和为零;
(4)如果ab<0,那么a>0,b<0.
解:(1)原命题是真命题.逆命题为:如果两条直线只有
一个交点,那么它们相交.逆命题是真命题.
(2)原命题是假命题.逆命题为:如果a2>b2,那么a
>b.逆命题是假命题.
(3)原命题是真命题.逆命题为:如果两个数的和为
零,那么它们互为相反数.逆命题是真命题.
(4)原命题是假命题.逆命题为:如果a>0,b<0,
那么ab<0.逆命题是真命题.
写出逆命题的关键是分清楚原命题的题设和结论,
然后将它的题设和结论交换位置就得到这个命题的逆
命题.判断一个命题是真命题需要进行逻辑推理,判
断一个命题是假命题只需要举出一个反例就可以了.
新知小结
1 说出下列命题的逆命题.这些逆命题成立吗?
(1)两条直线平行,内错角相等;
(2)如果两个实数相等,那么它们的绝对值相等;
(3)全等三角形的对应角相等;
(4)在角的内部,到角的两边距离相等的点在角
的平分线上.
巩固新知
(1)逆命题:内错角相等,两条直线平行.逆命题
成立.
(2)逆命题:如果两个实数的绝对值相等,那么这
两个实数相等.逆命题不成立.
(3)逆命题:三个角对应相等的两个三角形全等.
逆命题不成立.
(4)逆命题:角的平分线上的点到角两边的距离相
等.逆命题成立.
解:
已知下列命题:①若a>b,则ac>bc;②若a=1,则 =a;③内错角相等.其中原命题与逆命题均为真命题的个数是( )
A.0 B.1
C.2 D.3
2
A
下列定理中,没有逆定理的是( )
A.直角三角形的两锐角互余
B.若三角形三边长a,b,c (其中a<c,b<c)
满足a2+b2=c2,则该三角形是直角三角形
C.全等三角形的对应角相等
D.互为相反数的两数之和为0
3
C
2
知识点
勾股定理的逆定理
勾股定理的逆定理
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
勾股定理
如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形.
a2 + b2 = c2
互逆定理
合作探究
例2 判断由线段a,b,c组成的三角形是不是直角三角形:
(1)a=15,b=8,c=17;
(2)a=13,b=14,c =15.
分析:根据勾股定理及其逆定理,判断一个三角形是不是直
角三角形,只要看两条较小边长的平方和是否等于最
大边长的平方.
解:(1)因为 152+82=225+64=289,172 = 289,所以152 +82 =172 ,
根据勾股定理的逆定理,这个三角形是直角三角形.
(2)因为132+142=169+196=365,152=225,所以132+142≠
152,根据勾股定理,这个三角形不是直角三角形.
判断一个三角形是不是直角三角形有两种方法:
(1)利用定义,即如果已知条件与角度有关,可借助三角
形的内角和定理判断;
(2)利用直角三角形的判定条件,即若已知条件与边有关,
一般通过计算得出三边的数量关系(即a2+b2=c2)来判
断,看是否符合较短两边的平方和等于最长边的平方.
新知小结
例3 如图,某港口P位于东西方向的海岸线上.“远航”
号、“海天”号轮船同时离开港口,各自沿一固
定方向航行,“远航”号每小时航行 16 n mile,
“海天”号每小时航行12 n mile.它们离开港口一个
半小时后分别位于点Q,R处,且相距30 n mile.如
果知道“远航”号沿东北方
向航行,能知道“海天”号
沿哪个方向航行吗?
合作探究
分析:在图中可以看到,由于“远航”号的航向已知,
如果求出两艘轮船的航向所成的角,就能知道
“海天”号的航向了.
解:根据题意,PQ =16×1.5 = 24,PR=12×1.5 = 18,
QR=30.
因为 242+182=302,即 PQ2+PR2=QR2,
所以∠QPR= 90°.
由“远航”号沿东北方向航行可知,∠1=45°.
因此∠2=45°,即“海天”号沿西北方向航行.
用数学几何知识解决生活实际问题的关键是:建模
思想,即将实际问题转化为数学问题;这里要特别注意
弄清实际语言与数学语言间的关系;如本例中:“点与
点之间的最短路线”就是“连接这两点的线段”,“点
与直线的最短距离”就是“点到直线的垂线段的长”.
新知小结
1 如果三条线段长a,b,c满足a2=c2–b2,这三
条线段组成的三角形是不是直角三角形?为
什么?
这三条线段组成的三角形是直角三角形,因为三条线段长a,b,c满足a2=c2-b2,即a2+b2=c2,根据勾股定理的逆定理可知,三角形是直角三角形.
解:
巩固新知
2 在△ABC中,∠A,∠B,∠C的对边分别为a,b,
c,且(a+b)(a-b)=c2,则( )
A.∠A为直角 B.∠B为直角
C.∠C为直角 D.△ABC不是直角三角形
A
3 五根小木棒,其长度(单位:cm)分别为7,15,
20,24,25,现将它们摆成两个直角三角形,
其中正确的是( )
C
如图,△ABC的顶点在正方形网格的格点,若小方格的边长为1,则△ABC是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.以上都不对
4
B
△ABC的三边长分别为a,b,c,下列条件:
①∠A=∠B-∠C;
②∠A:∠B:∠C=3:4:5;
③a2=(b+c)(b-c);
④a:b:c=5:12:13.
其中能判定△ABC是直角三角形的有( )
A.1个 B.2个 C.3个 D.4个
5
C
3
知识点
勾 股 数
勾股数:能够成为直角三角形三条边长的三个
正整数.
常见的勾股数有:3,4,5;5,12,13;
8,15,17;7,24,25;9,40,41;….
合作探究
2.判断勾股数的方法:
(1)确定是否是三个正整数;
(2)确定最大数;
(3)计算:看较小两数的平方和是否等于最大数的
平方.
导引:根据勾股数的定义:满足a2+b2=c2的三个正整数
a,b,c称为勾股数.A.62+72≠82,不能构成勾
股数,故错误;B.52+82≠132,不能构成勾股数,
故错误;C.1.5和2.5不是整数,所以不能构成勾股
数,故错误;D.212+282=352,能构成勾股数,故
正确.故选D.
例4 下面四组数中是勾股数的一组是( )
A.6,7,8 B.5,8,13
C.1.5,2,2.5 D.21,28,35
D
确定勾股数的方法:首先看这三个数是否是正整
数;然后看较小两个数的平方和是否等于最大数的平
方,记住常见的勾股数(3,4,5;5,12,13;8,15,
17;7,24,25)可以提高解题速度.
新知小结
1 下面几组数中,为勾股数的一组是( )
A.4,5,6 B.12,16,20
C.-10,24,26 D.2.4,4.5,5.1
B
巩固新知
给出下列命题:
①如果a,b,c为一组勾股数,那么4a,4b,4c仍是一组勾股数;
②如果直角三角形的两边长分别是3和4,那么另一边长的平方必为25;
③如果一个三角形的三边长分别是12,25,21,那么此三角形必是直角三角形;
④一个等腰直角三角形的三边长分别是a,b,c,其中a是斜边长,那么a2∶b2∶c2=2∶1∶1.
其中正确的是( )
A.①② B.①③ C.①④ D.②④
2
C
逆定理
三角形两直角边分
别为a,b,斜边为
c,那么a2+b2=c2
定理
直角三角形!
1
知识小结
归纳新知
下列各组数能构成勾股数的是________.(填序号)
① 6,8,10; ② 7,8,10; ③
①
2
易错小结
易错点:忽视勾股数是正整数这一条件.
首先要注意到勾股数必须是一组正整数,其次要满足两个较小数的平方和等于最大数的平方.本题易误认为③也是勾股数.
易错总结:
互逆命题
逆命题
课后练习
逆定理
B
A
直角三角形
③
不能确定a2-b2是否为0
△ABC为等腰三角形或直角三角形
C
B
C
勾股数
①
D
解:∠A+∠B<∠C.
证明:如图,过点B作MN∥AC,
则∠MBA=∠A,∠NBC=∠C(两直线平行,内错角相等).
∵∠MBA+∠ABC+∠NBC=180°(平角的定义),
∴∠A+∠ABC+∠C=180°(等量代换),
即△ABC的内角和等于180°.
再 见
17.2.1 勾股定理的逆定理
人教版数学八年级下册
学习目标
1.能利用勾股定理的逆定理判定一个三角形是否为直角三角形.
2.灵活运用勾股定理及其逆定理解决问题.
3.理解原命题、逆命题、逆定理的概念及关系.
导入新知
同学们,古埃及人曾经用下面的方法画直角:将一根长绳打上等距离的13个结,然后用桩钉成一个三角形(如图),他们认为其中一个角便是直角.你知道这是什么道理吗?
勾股定理的逆定理
1
知识点
逆命题、逆定理
如果两个命题的题设、结论正好相反,那么这
两个命题称为互逆命题,如果把其中一个叫做
原命题,那么另一个叫做它的逆命题.
合作探究
2.如果一个定理的逆命题经过证明是正确的,那
么它也是一个定理,称其为原定理的逆定理,
这两个定理称为互逆定理.
导引:根据题目要求,先判断原命题的真假,再将原命题
的题设和结论互换,写出原命题的逆命题,最后判
断逆命题的真假.
例1 判断下列命题的真假,写出逆命题,并判断逆命题
的真假:
(1)如果两条直线相交,那么它们只有一个交点;
(2)如果a>b,那么a2>b2;
(3)如果两个数互为相反数,那么它们的和为零;
(4)如果ab<0,那么a>0,b<0.
解:(1)原命题是真命题.逆命题为:如果两条直线只有
一个交点,那么它们相交.逆命题是真命题.
(2)原命题是假命题.逆命题为:如果a2>b2,那么a
>b.逆命题是假命题.
(3)原命题是真命题.逆命题为:如果两个数的和为
零,那么它们互为相反数.逆命题是真命题.
(4)原命题是假命题.逆命题为:如果a>0,b<0,
那么ab<0.逆命题是真命题.
写出逆命题的关键是分清楚原命题的题设和结论,
然后将它的题设和结论交换位置就得到这个命题的逆
命题.判断一个命题是真命题需要进行逻辑推理,判
断一个命题是假命题只需要举出一个反例就可以了.
新知小结
1 说出下列命题的逆命题.这些逆命题成立吗?
(1)两条直线平行,内错角相等;
(2)如果两个实数相等,那么它们的绝对值相等;
(3)全等三角形的对应角相等;
(4)在角的内部,到角的两边距离相等的点在角
的平分线上.
巩固新知
(1)逆命题:内错角相等,两条直线平行.逆命题
成立.
(2)逆命题:如果两个实数的绝对值相等,那么这
两个实数相等.逆命题不成立.
(3)逆命题:三个角对应相等的两个三角形全等.
逆命题不成立.
(4)逆命题:角的平分线上的点到角两边的距离相
等.逆命题成立.
解:
已知下列命题:①若a>b,则ac>bc;②若a=1,则 =a;③内错角相等.其中原命题与逆命题均为真命题的个数是( )
A.0 B.1
C.2 D.3
2
A
下列定理中,没有逆定理的是( )
A.直角三角形的两锐角互余
B.若三角形三边长a,b,c (其中a<c,b<c)
满足a2+b2=c2,则该三角形是直角三角形
C.全等三角形的对应角相等
D.互为相反数的两数之和为0
3
C
2
知识点
勾股定理的逆定理
勾股定理的逆定理
如果直角三角形两直角边分别为a,b,斜边为c,那么
a2 + b2 = c2
勾股定理
如果三角形的三边长a、b、c满足
那么这个三角形是直角三角形.
a2 + b2 = c2
互逆定理
合作探究
例2 判断由线段a,b,c组成的三角形是不是直角三角形:
(1)a=15,b=8,c=17;
(2)a=13,b=14,c =15.
分析:根据勾股定理及其逆定理,判断一个三角形是不是直
角三角形,只要看两条较小边长的平方和是否等于最
大边长的平方.
解:(1)因为 152+82=225+64=289,172 = 289,所以152 +82 =172 ,
根据勾股定理的逆定理,这个三角形是直角三角形.
(2)因为132+142=169+196=365,152=225,所以132+142≠
152,根据勾股定理,这个三角形不是直角三角形.
判断一个三角形是不是直角三角形有两种方法:
(1)利用定义,即如果已知条件与角度有关,可借助三角
形的内角和定理判断;
(2)利用直角三角形的判定条件,即若已知条件与边有关,
一般通过计算得出三边的数量关系(即a2+b2=c2)来判
断,看是否符合较短两边的平方和等于最长边的平方.
新知小结
例3 如图,某港口P位于东西方向的海岸线上.“远航”
号、“海天”号轮船同时离开港口,各自沿一固
定方向航行,“远航”号每小时航行 16 n mile,
“海天”号每小时航行12 n mile.它们离开港口一个
半小时后分别位于点Q,R处,且相距30 n mile.如
果知道“远航”号沿东北方
向航行,能知道“海天”号
沿哪个方向航行吗?
合作探究
分析:在图中可以看到,由于“远航”号的航向已知,
如果求出两艘轮船的航向所成的角,就能知道
“海天”号的航向了.
解:根据题意,PQ =16×1.5 = 24,PR=12×1.5 = 18,
QR=30.
因为 242+182=302,即 PQ2+PR2=QR2,
所以∠QPR= 90°.
由“远航”号沿东北方向航行可知,∠1=45°.
因此∠2=45°,即“海天”号沿西北方向航行.
用数学几何知识解决生活实际问题的关键是:建模
思想,即将实际问题转化为数学问题;这里要特别注意
弄清实际语言与数学语言间的关系;如本例中:“点与
点之间的最短路线”就是“连接这两点的线段”,“点
与直线的最短距离”就是“点到直线的垂线段的长”.
新知小结
1 如果三条线段长a,b,c满足a2=c2–b2,这三
条线段组成的三角形是不是直角三角形?为
什么?
这三条线段组成的三角形是直角三角形,因为三条线段长a,b,c满足a2=c2-b2,即a2+b2=c2,根据勾股定理的逆定理可知,三角形是直角三角形.
解:
巩固新知
2 在△ABC中,∠A,∠B,∠C的对边分别为a,b,
c,且(a+b)(a-b)=c2,则( )
A.∠A为直角 B.∠B为直角
C.∠C为直角 D.△ABC不是直角三角形
A
3 五根小木棒,其长度(单位:cm)分别为7,15,
20,24,25,现将它们摆成两个直角三角形,
其中正确的是( )
C
如图,△ABC的顶点在正方形网格的格点,若小方格的边长为1,则△ABC是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.以上都不对
4
B
△ABC的三边长分别为a,b,c,下列条件:
①∠A=∠B-∠C;
②∠A:∠B:∠C=3:4:5;
③a2=(b+c)(b-c);
④a:b:c=5:12:13.
其中能判定△ABC是直角三角形的有( )
A.1个 B.2个 C.3个 D.4个
5
C
3
知识点
勾 股 数
勾股数:能够成为直角三角形三条边长的三个
正整数.
常见的勾股数有:3,4,5;5,12,13;
8,15,17;7,24,25;9,40,41;….
合作探究
2.判断勾股数的方法:
(1)确定是否是三个正整数;
(2)确定最大数;
(3)计算:看较小两数的平方和是否等于最大数的
平方.
导引:根据勾股数的定义:满足a2+b2=c2的三个正整数
a,b,c称为勾股数.A.62+72≠82,不能构成勾
股数,故错误;B.52+82≠132,不能构成勾股数,
故错误;C.1.5和2.5不是整数,所以不能构成勾股
数,故错误;D.212+282=352,能构成勾股数,故
正确.故选D.
例4 下面四组数中是勾股数的一组是( )
A.6,7,8 B.5,8,13
C.1.5,2,2.5 D.21,28,35
D
确定勾股数的方法:首先看这三个数是否是正整
数;然后看较小两个数的平方和是否等于最大数的平
方,记住常见的勾股数(3,4,5;5,12,13;8,15,
17;7,24,25)可以提高解题速度.
新知小结
1 下面几组数中,为勾股数的一组是( )
A.4,5,6 B.12,16,20
C.-10,24,26 D.2.4,4.5,5.1
B
巩固新知
给出下列命题:
①如果a,b,c为一组勾股数,那么4a,4b,4c仍是一组勾股数;
②如果直角三角形的两边长分别是3和4,那么另一边长的平方必为25;
③如果一个三角形的三边长分别是12,25,21,那么此三角形必是直角三角形;
④一个等腰直角三角形的三边长分别是a,b,c,其中a是斜边长,那么a2∶b2∶c2=2∶1∶1.
其中正确的是( )
A.①② B.①③ C.①④ D.②④
2
C
逆定理
三角形两直角边分
别为a,b,斜边为
c,那么a2+b2=c2
定理
直角三角形!
1
知识小结
归纳新知
下列各组数能构成勾股数的是________.(填序号)
① 6,8,10; ② 7,8,10; ③
①
2
易错小结
易错点:忽视勾股数是正整数这一条件.
首先要注意到勾股数必须是一组正整数,其次要满足两个较小数的平方和等于最大数的平方.本题易误认为③也是勾股数.
易错总结:
互逆命题
逆命题
课后练习
逆定理
B
A
直角三角形
③
不能确定a2-b2是否为0
△ABC为等腰三角形或直角三角形
C
B
C
勾股数
①
D
解:∠A+∠B<∠C.
证明:如图,过点B作MN∥AC,
则∠MBA=∠A,∠NBC=∠C(两直线平行,内错角相等).
∵∠MBA+∠ABC+∠NBC=180°(平角的定义),
∴∠A+∠ABC+∠C=180°(等量代换),
即△ABC的内角和等于180°.
再 见
