7.2 探索直线平行的条件 同步练习(含答案)
文档属性
| 名称 | 7.2 探索直线平行的条件 同步练习(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-12 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第七章 相交线与平行线
2 探索直线平行的条件
知识能力全练
知识点一 同位角
1.下列图形中,∠1与∠2是同位角的是( )
2.如图所示,∠B的同位角是( )
知识点二 利用同位角判定两直线平行
3.我们学过用直尺和三角尺画平行线的方法,如图所示,直线a∥b的根据是___________
______________________________.
4.如图所示,直线EF分别与直线AB、CD交于M,N两点,∠1=55°,∠2=125°,求证:AB∥CD(要求写出最后一步的理论依据).
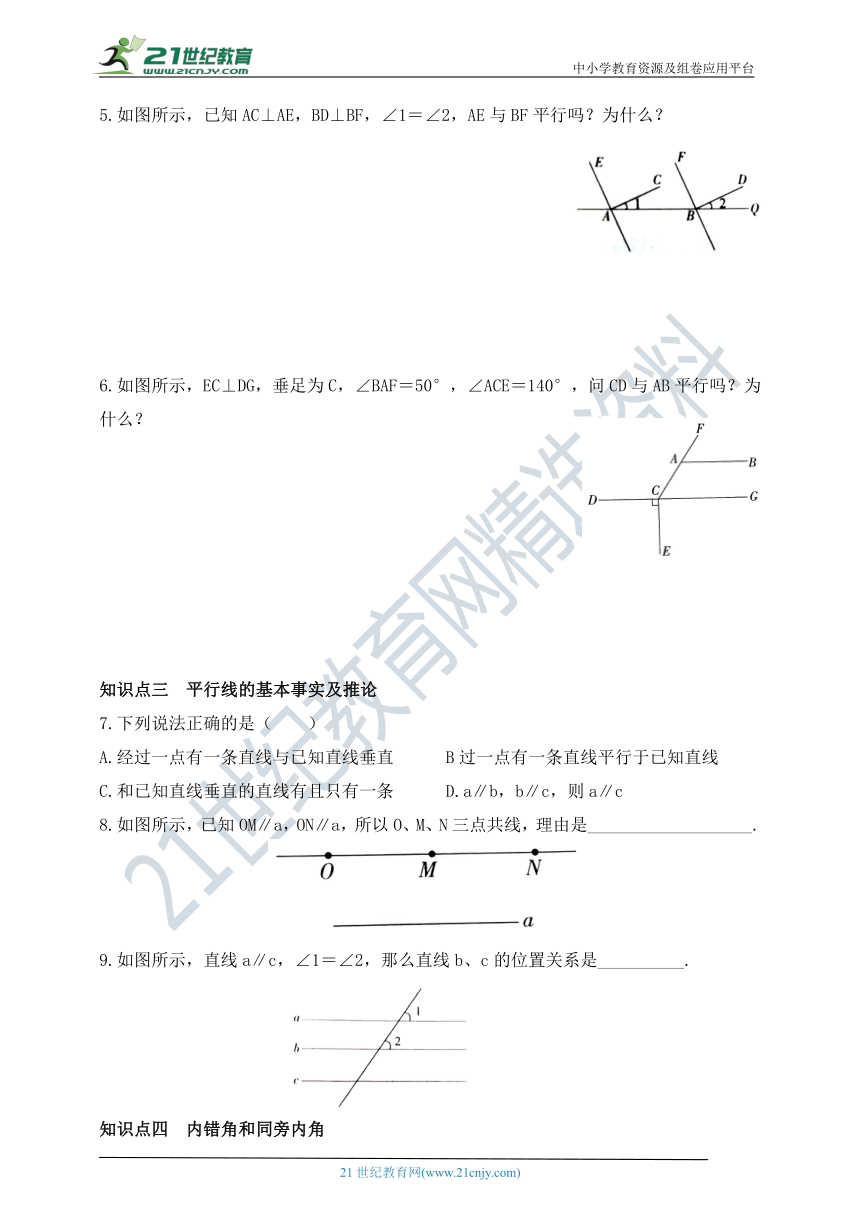
5.如图所示,已知AC⊥AE,BD⊥BF,∠1=∠2,AE与BF平行吗?为什么?
6.如图所示,EC⊥DG,垂足为C,∠BAF=50°,∠ACE=140°,问CD与AB平行吗?为什么?
知识点三 平行线的基本事实及推论
7.下列说法正确的是( )
A.经过一点有一条直线与已知直线垂直 B过一点有一条直线平行于已知直线
C.和已知直线垂直的直线有且只有一条 D.a∥b,b∥c,则a∥c
8.如图所示,已知OM∥a,ON∥a,所以O、M、N三点共线,理由是___________________.
9.如图所示,直线a∥c,∠1=∠2,那么直线b、c的位置关系是__________.
知识点四 内错角和同旁内角
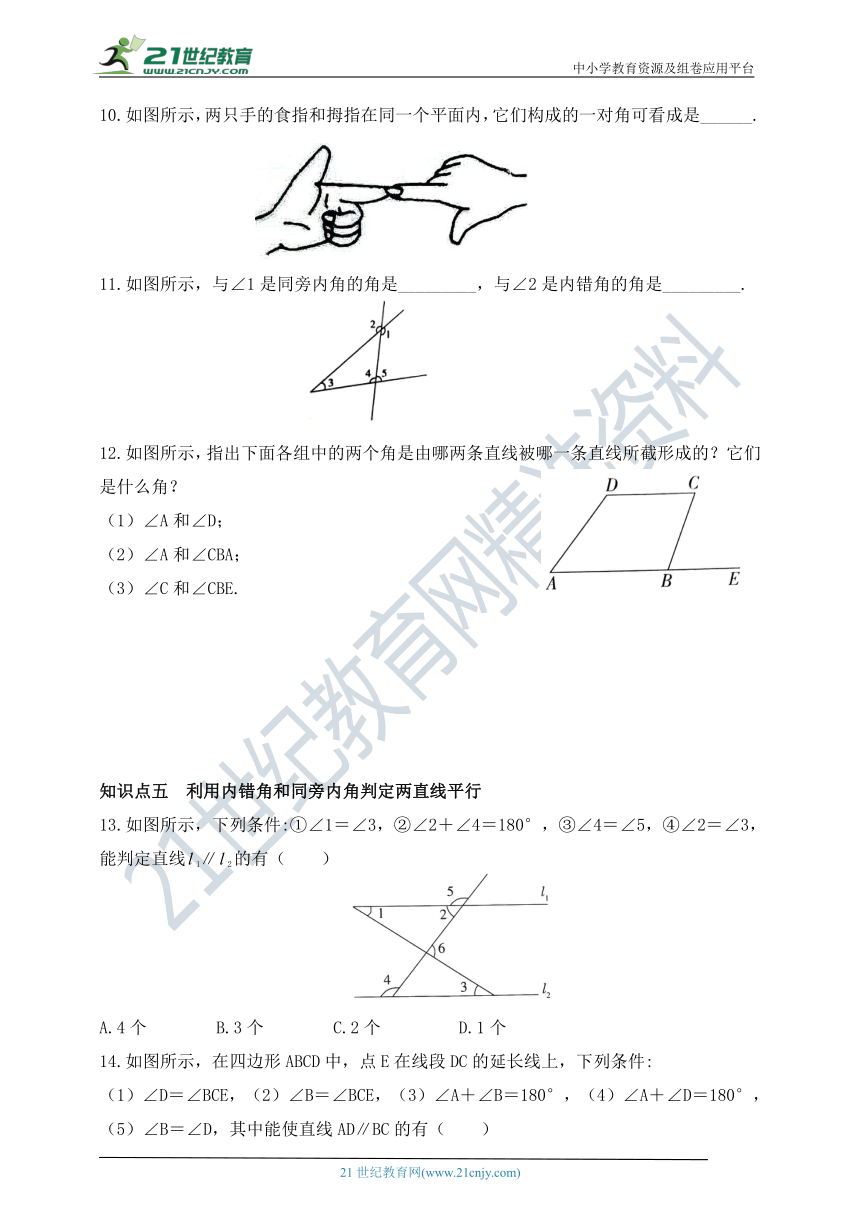
10.如图所示,两只手的食指和拇指在同一个平面内,它们构成的一对角可看成是______.
11.如图所示,与∠1是同旁内角的角是_________,与∠2是内错角的角是_________.
12.如图所示,指出下面各组中的两个角是由哪两条直线被哪一条直线所截形成的?它们是什么角?
(1)∠A和∠D;
(2)∠A和∠CBA;
(3)∠C和∠CBE.
知识点五 利用内错角和同旁内角判定两直线平行
13.如图所示,下列条件:①∠1=∠3,②∠2+∠4=180°,③∠4=∠5,④∠2=∠3,能判定直线1∥2的有( )
A.4个 B.3个 C.2个 D.1个
14.如图所示,在四边形ABCD中,点E在线段DC的延长线上,下列条件:
(1)∠D=∠BCE,(2)∠B=∠BCE,(3)∠A+∠B=180°,(4)∠A+∠D=180°,(5)∠B=∠D,其中能使直线AD∥BC的有( )
A.1个 B.2个 C.3个 D.4个
15.如图所示,A、B之间是一座山,一条铁路要过A、B两县,在A地测得铁路走向是北偏东64°,那么B地按南偏西_________的方向施工,才能使铁路在山腰中准确接通.
16.请将下列证明过程补充完整:
已知:如图所示,AE平分∠BAC,CE平分∠ACD且∠a+∠β=90°.
求证:AB∥CD.
证明:因为CE平分∠ACD(已知),
所以∠ACD=2∠a(___________).
因为AE平分∠BAC(已知),
所以∠BAC=__________(角平分线的定义).
所以∠ACD+∠BAC=2∠a+2∠β(等式的性质),即∠ACD+∠BAC=2(∠a+∠β).
因为∠a+∠β=90°(已知),
所以∠ACD+∠BAC=_______________(等量代换).
所以AB∥CD(______________________).
17.如图所示,已知∠COF+∠C=180°,∠C=∠B.求证:AB∥EF.
18.如图所示,已知∠ABC=∠D,∠ABC+∠FCB=180°,∠FMN=∠FCE.求证:MN∥DG.
巩固提高全练
19.如图所示,下列关于∠1,∠2,∠3,∠4,∠5的说法不正确的是( )
A.同旁内角有2对 B.内错角有1对 C.同位角有1对 D.对顶角有1对
20.如图所示,下列条件能判定EB∥AC的是( )
A.∠C=∠ABE B.∠BAC=∠EBD C.∠ABC=∠BAE D.∠BAC=∠ABE
21.如图所示,DE平分∠ADC,CE平分∠BCD,且∠1+∠2=90°试判断AD与BC的位置关系,并说明理由.
22.如图所示,直线a,b被直线c,d所截.下列条件能判定a∥b的是( )
A.∠1=∠3 B.∠2+∠4=180° C.∠4=∠5 D.∠1=∠2
23.如图所示,不能判定AB∥CD的是( )
A.∠B=∠DCE B.∠A=∠ACD C.∠B+∠BCD=180° D.∠A=∠DCE
24.如图所示,请填写一个条件,使结论成立:因为____________________,所以a∥b.
25.如图所示,用符号语言表达定理“同旁内角互补,两直线平行”的推理形式:因为,所以a∥b.
26.如图所示,∠BEC=95°,∠ABE=120°,∠DCE=35°,则AB与CD平行吗?请说明理由.
27.我们常把复杂的数学问题分解为基本问题来研究,化繁为简,这是一种常见的数
学解题思想.
(1)如图①,直线1,2被直线3所截,在这个基本图形中,形成了_____对同旁内角;
(2)如图②,平面内三条直线1,2,3两两相交,交点分别为A、B、C,图中一共有_______对同旁内角;
(3)平面内四条直线两两相交,最多可以形成________对同旁内角;
(4)平面内n条直线两两相交,最多可以形成________对同旁内角.
参考答案
1.C
2.答案 ∠FEC,∠AFD,∠AFE
3.答案 同位角相等,两直线平行
4.证明 因为∠1=55°,所以∠CNF=125°,
因为∠2=125°,所以∠CNF=∠2,
所以AB∥CD(同位角相等,两直线平行)
5.解析 平行
理由:因为AC⊥AE,BD⊥BF,所以∠EAC=∠FBD=90°,
因为∠1=∠2,所以∠EAC+∠1=∠FBD+∠2,即∠EAB=∠FBQ,
所以AE∥BF(同位角相等,两直线平行)
6.解析 AB∥CD.
理由:因为EC⊥DG,所以∠ECG=90°,
因为∠ACE=140°,所以∠ACG=140°-90°=50°,
因为∠BAF=50°,所以∠BAF=∠ACG,所以AB∥CD.
7.D 8.答案 经过直线外一点,有且只有一条直线与这条直线平行
9.答案 b∥c 10.答案 内错角 11.答案 ∠5;∠3
12.解析(1)∠A和∠D是由直线AE、CD被直线AD所截形成的,它们是同旁内角.
(2)∠A和∠CBA是由直线AD、BC被直线AE所截形成的,它们是同旁内角.
(3)∠C和∠CBE是由直线CD、AE被直线BC所截形成的,它们是内错角.
13.B 14.B 15.答案 64°
16.答案 角平分线的定义2∠B;180°;同旁内角互补,两直线平行
17.证明 因为∠COF+∠C=180°,所以EF∥CD,
因为∠C=∠B,所以AB∥CD,所以AB∥EF.
18.证明 因为∠ABC=∠D,∠ABC+∠FCB=180(已知),
所以∠D+∠FCB=180°(等量代换)
因为∠ECD=∠FCB(对顶角相等),所以∠D+∠ECD=180°(等量代换),
所以BE∥DG(同旁内角互补,两直线平行).
因为∠FMN=∠FCE(已知),所以MN∥BE(同位角相等,两直线平行),
所以MN∥DG(平行于同一条直线的两直线平行).
19.C 20.D
21.解析 AD∥BC理由如下:
∵DE平分∠ADC,CE平分∠BCD,∴∠ADC=2∠1,∠BCD=2∠2,
∵∠1+∠2=90°,∴∠ADC+∠BCD=180°,∴AD∥BC.
22.D 23.D
24.答案 ∠1=∠4或∠2=∠4或∠3+∠4=180°(写一个即可)
25.答案 ∠1+∠3=180°
26.解析 AB∥CD理由:如图,作∠FEC=35°因为∠DCE=35°,所以∠FEC=∠DCE,所以EF∥CD.因为∠BEC=95°,所以∠BEF=60°因为∠ABE=120°,所以∠BEF+∠ABE=180°,所以AB∥EF.根据“平行于同一直线的两直线平行”,可得AB∥CD.
27.解析 (1)2. (2)6. (3)24. (4)n(n-1)(n-2).
_21?????????è?????(www.21cnjy.com)_
第七章 相交线与平行线
2 探索直线平行的条件
知识能力全练
知识点一 同位角
1.下列图形中,∠1与∠2是同位角的是( )
2.如图所示,∠B的同位角是( )
知识点二 利用同位角判定两直线平行
3.我们学过用直尺和三角尺画平行线的方法,如图所示,直线a∥b的根据是___________
______________________________.
4.如图所示,直线EF分别与直线AB、CD交于M,N两点,∠1=55°,∠2=125°,求证:AB∥CD(要求写出最后一步的理论依据).
5.如图所示,已知AC⊥AE,BD⊥BF,∠1=∠2,AE与BF平行吗?为什么?
6.如图所示,EC⊥DG,垂足为C,∠BAF=50°,∠ACE=140°,问CD与AB平行吗?为什么?
知识点三 平行线的基本事实及推论
7.下列说法正确的是( )
A.经过一点有一条直线与已知直线垂直 B过一点有一条直线平行于已知直线
C.和已知直线垂直的直线有且只有一条 D.a∥b,b∥c,则a∥c
8.如图所示,已知OM∥a,ON∥a,所以O、M、N三点共线,理由是___________________.
9.如图所示,直线a∥c,∠1=∠2,那么直线b、c的位置关系是__________.
知识点四 内错角和同旁内角
10.如图所示,两只手的食指和拇指在同一个平面内,它们构成的一对角可看成是______.
11.如图所示,与∠1是同旁内角的角是_________,与∠2是内错角的角是_________.
12.如图所示,指出下面各组中的两个角是由哪两条直线被哪一条直线所截形成的?它们是什么角?
(1)∠A和∠D;
(2)∠A和∠CBA;
(3)∠C和∠CBE.
知识点五 利用内错角和同旁内角判定两直线平行
13.如图所示,下列条件:①∠1=∠3,②∠2+∠4=180°,③∠4=∠5,④∠2=∠3,能判定直线1∥2的有( )
A.4个 B.3个 C.2个 D.1个
14.如图所示,在四边形ABCD中,点E在线段DC的延长线上,下列条件:
(1)∠D=∠BCE,(2)∠B=∠BCE,(3)∠A+∠B=180°,(4)∠A+∠D=180°,(5)∠B=∠D,其中能使直线AD∥BC的有( )
A.1个 B.2个 C.3个 D.4个
15.如图所示,A、B之间是一座山,一条铁路要过A、B两县,在A地测得铁路走向是北偏东64°,那么B地按南偏西_________的方向施工,才能使铁路在山腰中准确接通.
16.请将下列证明过程补充完整:
已知:如图所示,AE平分∠BAC,CE平分∠ACD且∠a+∠β=90°.
求证:AB∥CD.
证明:因为CE平分∠ACD(已知),
所以∠ACD=2∠a(___________).
因为AE平分∠BAC(已知),
所以∠BAC=__________(角平分线的定义).
所以∠ACD+∠BAC=2∠a+2∠β(等式的性质),即∠ACD+∠BAC=2(∠a+∠β).
因为∠a+∠β=90°(已知),
所以∠ACD+∠BAC=_______________(等量代换).
所以AB∥CD(______________________).
17.如图所示,已知∠COF+∠C=180°,∠C=∠B.求证:AB∥EF.
18.如图所示,已知∠ABC=∠D,∠ABC+∠FCB=180°,∠FMN=∠FCE.求证:MN∥DG.
巩固提高全练
19.如图所示,下列关于∠1,∠2,∠3,∠4,∠5的说法不正确的是( )
A.同旁内角有2对 B.内错角有1对 C.同位角有1对 D.对顶角有1对
20.如图所示,下列条件能判定EB∥AC的是( )
A.∠C=∠ABE B.∠BAC=∠EBD C.∠ABC=∠BAE D.∠BAC=∠ABE
21.如图所示,DE平分∠ADC,CE平分∠BCD,且∠1+∠2=90°试判断AD与BC的位置关系,并说明理由.
22.如图所示,直线a,b被直线c,d所截.下列条件能判定a∥b的是( )
A.∠1=∠3 B.∠2+∠4=180° C.∠4=∠5 D.∠1=∠2
23.如图所示,不能判定AB∥CD的是( )
A.∠B=∠DCE B.∠A=∠ACD C.∠B+∠BCD=180° D.∠A=∠DCE
24.如图所示,请填写一个条件,使结论成立:因为____________________,所以a∥b.
25.如图所示,用符号语言表达定理“同旁内角互补,两直线平行”的推理形式:因为,所以a∥b.
26.如图所示,∠BEC=95°,∠ABE=120°,∠DCE=35°,则AB与CD平行吗?请说明理由.
27.我们常把复杂的数学问题分解为基本问题来研究,化繁为简,这是一种常见的数
学解题思想.
(1)如图①,直线1,2被直线3所截,在这个基本图形中,形成了_____对同旁内角;
(2)如图②,平面内三条直线1,2,3两两相交,交点分别为A、B、C,图中一共有_______对同旁内角;
(3)平面内四条直线两两相交,最多可以形成________对同旁内角;
(4)平面内n条直线两两相交,最多可以形成________对同旁内角.
参考答案
1.C
2.答案 ∠FEC,∠AFD,∠AFE
3.答案 同位角相等,两直线平行
4.证明 因为∠1=55°,所以∠CNF=125°,
因为∠2=125°,所以∠CNF=∠2,
所以AB∥CD(同位角相等,两直线平行)
5.解析 平行
理由:因为AC⊥AE,BD⊥BF,所以∠EAC=∠FBD=90°,
因为∠1=∠2,所以∠EAC+∠1=∠FBD+∠2,即∠EAB=∠FBQ,
所以AE∥BF(同位角相等,两直线平行)
6.解析 AB∥CD.
理由:因为EC⊥DG,所以∠ECG=90°,
因为∠ACE=140°,所以∠ACG=140°-90°=50°,
因为∠BAF=50°,所以∠BAF=∠ACG,所以AB∥CD.
7.D 8.答案 经过直线外一点,有且只有一条直线与这条直线平行
9.答案 b∥c 10.答案 内错角 11.答案 ∠5;∠3
12.解析(1)∠A和∠D是由直线AE、CD被直线AD所截形成的,它们是同旁内角.
(2)∠A和∠CBA是由直线AD、BC被直线AE所截形成的,它们是同旁内角.
(3)∠C和∠CBE是由直线CD、AE被直线BC所截形成的,它们是内错角.
13.B 14.B 15.答案 64°
16.答案 角平分线的定义2∠B;180°;同旁内角互补,两直线平行
17.证明 因为∠COF+∠C=180°,所以EF∥CD,
因为∠C=∠B,所以AB∥CD,所以AB∥EF.
18.证明 因为∠ABC=∠D,∠ABC+∠FCB=180(已知),
所以∠D+∠FCB=180°(等量代换)
因为∠ECD=∠FCB(对顶角相等),所以∠D+∠ECD=180°(等量代换),
所以BE∥DG(同旁内角互补,两直线平行).
因为∠FMN=∠FCE(已知),所以MN∥BE(同位角相等,两直线平行),
所以MN∥DG(平行于同一条直线的两直线平行).
19.C 20.D
21.解析 AD∥BC理由如下:
∵DE平分∠ADC,CE平分∠BCD,∴∠ADC=2∠1,∠BCD=2∠2,
∵∠1+∠2=90°,∴∠ADC+∠BCD=180°,∴AD∥BC.
22.D 23.D
24.答案 ∠1=∠4或∠2=∠4或∠3+∠4=180°(写一个即可)
25.答案 ∠1+∠3=180°
26.解析 AB∥CD理由:如图,作∠FEC=35°因为∠DCE=35°,所以∠FEC=∠DCE,所以EF∥CD.因为∠BEC=95°,所以∠BEF=60°因为∠ABE=120°,所以∠BEF+∠ABE=180°,所以AB∥EF.根据“平行于同一直线的两直线平行”,可得AB∥CD.
27.解析 (1)2. (2)6. (3)24. (4)n(n-1)(n-2).
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
