2020-2021学年七年级数学苏科版下册第7章 平面图形的认识(二)周末培优卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年七年级数学苏科版下册第7章 平面图形的认识(二)周末培优卷(Word版 含解析) | 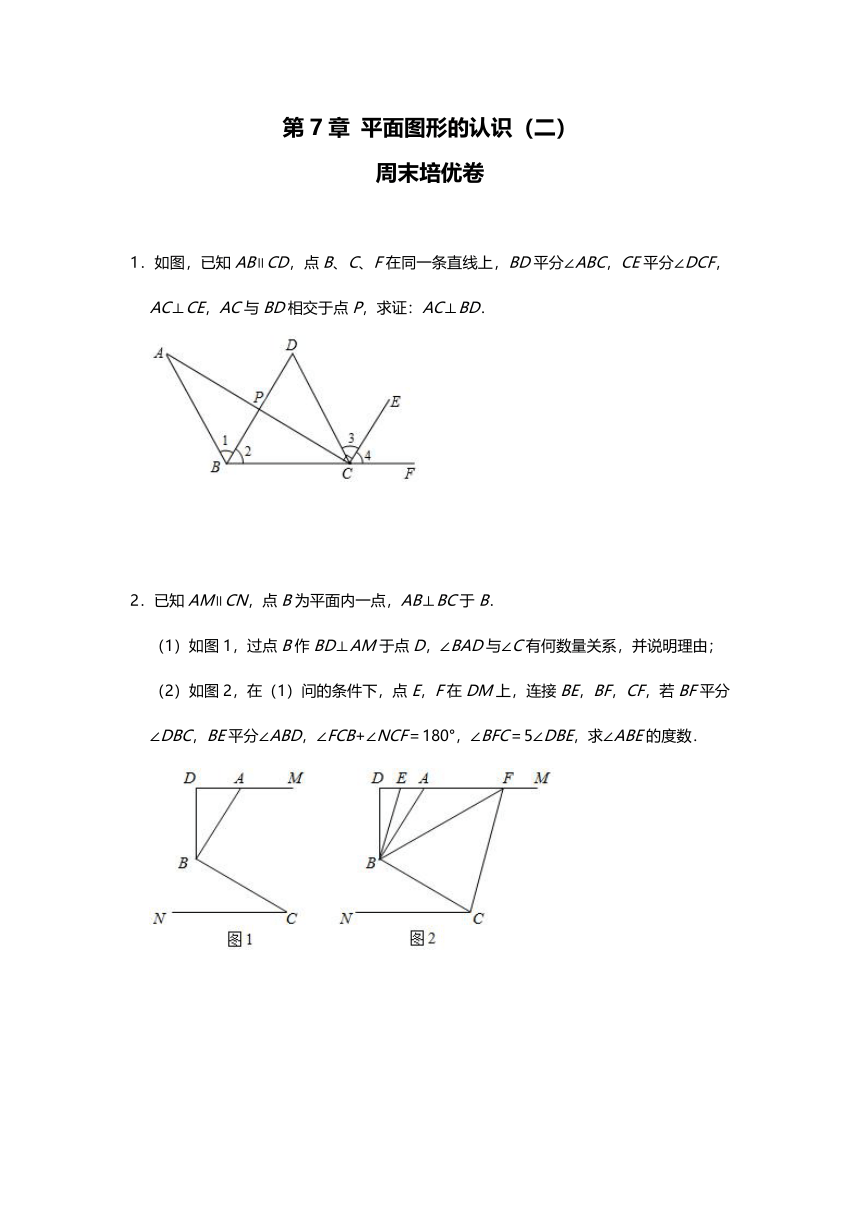 | |
| 格式 | doc | ||
| 文件大小 | 366.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-12 13:45:07 | ||
图片预览




文档简介
第7章 平面图形的认识(二)
周末培优卷
1.如图,已知AB∥CD,点B、C、F在同一条直线上,BD平分∠ABC,CE平分∠DCF,AC⊥CE,AC与BD相交于点P,求证:AC⊥BD.
2.已知AM∥CN,点B为平面内一点,AB⊥BC于B.
(1)如图1,过点B作BD⊥AM于点D,∠BAD与∠C有何数量关系,并说明理由;
(2)如图2,在(1)问的条件下,点E,F在DM上,连接BE,BF,CF,若BF平分∠DBC,BE平分∠ABD,∠FCB+∠NCF=180°,∠BFC=5∠DBE,求∠ABE的度数.
3.已知如图,直线EF与AB、CD分别相交于点E、F.
(1)如图1,若∠1=120°,∠2=60°,求证AB∥CD;
(2)在(1)的情况下,若点P是平面内的一个动点,连结PE、PF,探索∠EPF、∠PEB、∠PFD三个角之间的关系;
①当点P在图2的位置时,可得∠EPF=∠PEB+∠PFD;
请阅读下面的解答过程,并填空(理由或数学式)
解:如图2,过点P作MN∥AB,
则∠EPM=∠PEB .
∵AB∥CD(已知),MN∥AB(作图)
∴MN∥CD .
∴∠MPF=∠PFD
∴∠ +∠ =∠PEB+∠PFD(等式的性质)
即∠EPF=∠PEB+∠PFD
②当点P在图3的位置时,∠EPF、∠PEB、∠PFD三个角之间有何关系并证明.
③当点P在图4的位置时,请直接写出∠EPF、∠PEB、∠PFD三个角之间的关系: .
4.根据下面解答过程,完成下面填空:
如图,已知AB∥CD∥EF,∠A=105°,∠ACE=51°,求∠E的度数.
5.推理填空
已知:如图所示,点B,C,E在同一条直线上,AB∥CD,∠1=∠2,∠3=∠4,求证:AD∥BE
证明:∵AB∥CD(已知)
∴∠4=∠ ( )
∵∠3=∠4(已知)∴∠3=∠ ( )
∴∠1=∠2(已知)∴∠1+∠CAF=∠2+∠CAF(等式的性质)
即∠BAF=∠DAC
∴∠3=∠ (等量代换)
∴AD∥BE( )
6.如果一个角的两边与另一个角的两边分别平行,某同学为了探究这两个角之间的关系,画出了以下两个不同的图形,请你根据图形完成以下问题:
(1)如图①,如果AB∥CD,BE∥DF,那么∠1与∠2的关系是 ;
如图②,如果AB∥CD,BE∥DF,那么∠1与∠2的关系是 .
(2)根据(1)的探究过程,我们可得出结论:如果一个角的两边与另一个角的两边分别平行,那么这两个角 ;
(3)利用结论解决问题:如果有两个角的两边分别平行,且一个角比另一个角的3倍少60°,则这两个角分别是多少度?
7.完成下面证明
已知,如图,AB∥EF,∠1=∠2,∠3=∠4,AF与BE平行吗?为什么?
解:AF∥BE
理由:
∵AB∥EF(已知)
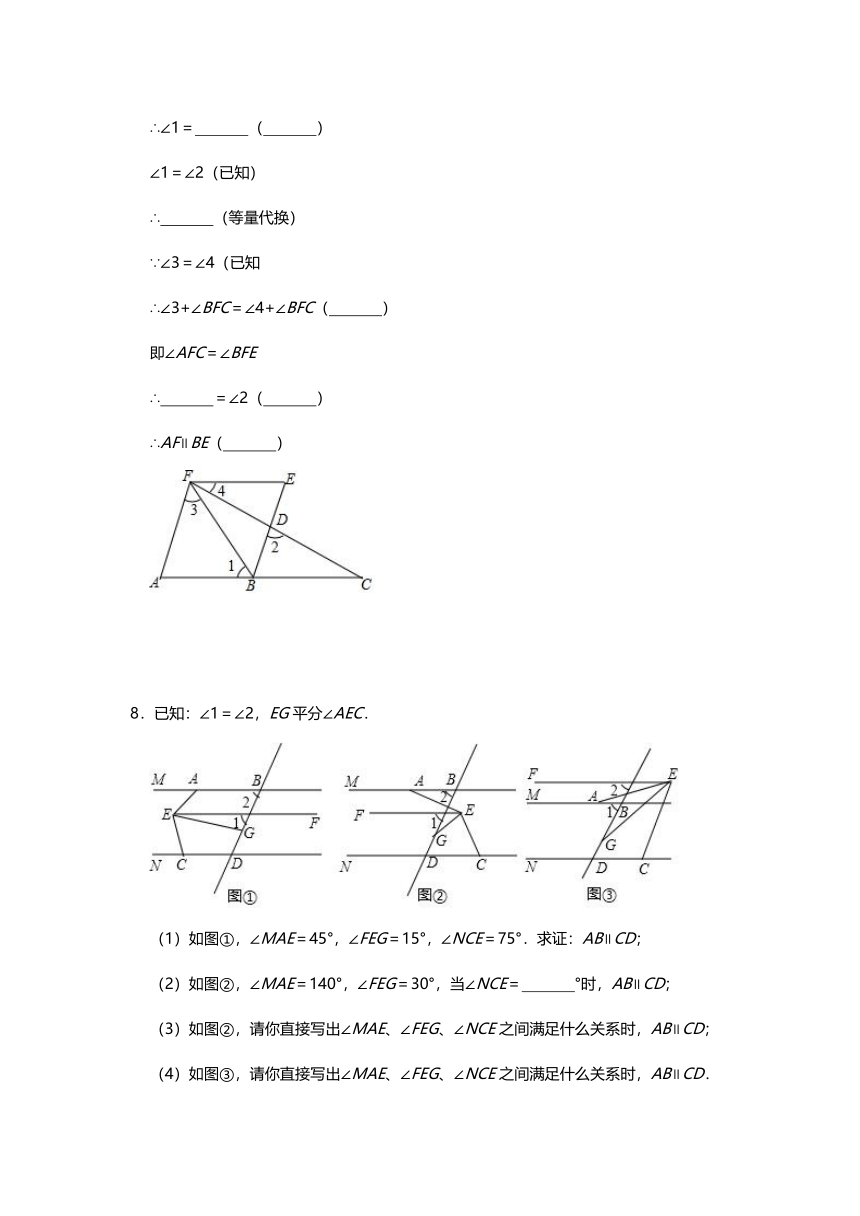
∴∠1= ( )
∠1=∠2(已知)
∴ (等量代换)
∵∠3=∠4(已知
∴∠3+∠BFC=∠4+∠BFC( )
即∠AFC=∠BFE
∴ =∠2( )
∴AF∥BE( )
8.已知:∠1=∠2,EG平分∠AEC.
(1)如图①,∠MAE=45°,∠FEG=15°,∠NCE=75°.求证:AB∥CD;
(2)如图②,∠MAE=140°,∠FEG=30°,当∠NCE= °时,AB∥CD;
(3)如图②,请你直接写出∠MAE、∠FEG、∠NCE之间满足什么关系时,AB∥CD;
(4)如图③,请你直接写出∠MAE、∠FEG、∠NCE之间满足什么关系时,AB∥CD.
9.有两个∠AOB与∠EDC,∠EDC保持不动,且∠EDC的一边CD∥AO,另一边DE与直线OB相交于点F.
(1)若∠AOB=40°,∠EDC=55°,解答下列问题:
①如图,当点E、O、D在同一条直线上,即点O与点F重合,则∠BOE= ;
②当点E、O、D不在同一条直线上,画出图形并求∠BFE的度数;
(2)在(1)②的前提下,若∠AOB=α,∠EDC=β,且α<β,请直接写出∠BFE的度数(用含α、β的式子表示).
10.如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并证明你的结论.
解:∠C与∠AED相等,理由如下:
∵∠1+∠2=180°(已知)
∠1+ =180°(邻补角定义)
∴∠2= ( )
∴AB∥ (内错角相等,两直线平行)
∴∠3= (两直线平行,内错角相等)
又∵∠3=∠B(已知)
∴∠B= (等量代换)
∴DE∥ (同位角相等,两直线平行)
∴∠C= (两直线平行,同位角相等)
11.如图1,已知∠A+∠E+∠F+∠C=540°.
(1)试判断直线AB与CD的位置关系,并说明理由
(2)如图2,∠PAB=3∠PAQ,∠PCD=3∠PCQ,试判断∠APC与∠AQC的数量关系,并说明理由.
12.如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E.∠ADC=70°.
(1)求∠EDC的度数;
(2)若∠ABC=n°,求∠BED的度数(用含n的式子表示);
(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示),不改变,请说明理由.
13.如图1,直线AB∥CD,点P在两平行线之间,点E在AB上,点F在CD上,连结PE,PF.
(1)若∠PEB=60°,∠PFD=50°,请求出∠EPF.(请写出必要的步骤说明理由)
(2)如图2,若点P、Q在直线AB与CD之间时,∠1=30°,∠2=40°,∠3=70°,请求出∠P4= .(不需说明理由,请直接写出答案)
(3)如图3,作P1E平分∠PEB,P1F平分∠PFD,若设∠PEB=x°,∠PFD=y°则∠EP1F= (用x、y的代数式表示),若P2E平分∠P1EB,P2F平分∠P1FD,可得∠EP2F;P3E平分∠P2EB,P3F平分∠P2FD,可得∠EP3F,依次平分下去,则∠EPnF= .
(4)在一次综合实践活动课上,张开同学制作了一个图5的“回旋镖“,经测量发现∠PAC=38°,∠PBC=22°,请你找出∠APB与∠C的数量关系并说明理由
14.如图,已知直线l1∥l2,点A、B分别在l1与l2上.直线l3和直线l1、l2交于点C和D,在直线CD上有一点P.
(1)如果P点在C、D之间运动时,问∠PAC,∠APB,∠PBD有怎样的数量关系?请说明理由.
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?
15.探究与发现:有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C.请写出∠BDC与∠A+∠ABD+∠ACD之间的数量关系,并说明理由.
应用:某零件如图所示,图纸要求∠A=90°,∠B=32°,∠C=21°,当检验员量得∠BDC=145°,就断定这个零件不合格,你能说出其中的道理吗?
参考答案
1.证明:∵AB∥CD,
∴∠ABC=∠DCF,
∵BD平分∠ABC,CE平分∠DCF,
∴∠1=∠2=∠3=∠4,
∵AC⊥CE,
∴∠4+∠PCB=90°,
∴∠2+∠PCB=90°,
∴∠BPC=90°,
∴AC⊥BD.
2.解:(1)如图1,过点B作BG∥DM,
∵BD⊥AM,
∴∠ABD+∠BAD=90°,DB⊥BG,即∠ABD+∠ABG=90°,
又∵AB⊥BC,
∴∠CBG+∠ABG=90°,
∴∠ABD=∠CBG,
∵AM∥CN,BG∥AM,
∴CN∥BG,
∴∠C=∠CBG,
∴∠ABD=∠C,
∴∠C+∠BAD=90°;
(2)如图2,过点B作BG∥DM,
∵BF平分∠DBC,BE平分∠ABD,
∴∠DBF=∠CBF,∠DBE=∠ABE,
由(1)可得∠ABD=∠CBG,
∴∠ABF=∠GBF,
设∠DBE=α,∠ABF=β,则
∠ABE=α,∠ABD=2α=∠CBG,∠GBF=β=∠AFB,∠BFC=5∠DBE=5α,
∴∠AFC=5α+β,
∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,
∴∠FCB=∠AFC=5α+β,
△BCF中,由∠CBF+∠BFC+∠BCF=180°,可得
(2α+β)+5α+(5α+β)=180°,①
由AB⊥BC,可得
β+β+2α=90°,②
由①②联立方程组,解得α=9°,
∴∠ABE=9°.
3.解:(1)∵∠1=120°,
∴∠BEF=120°,
又∵∠2=60°,
∴∠2+∠BEF=180°,
∴AB∥CD;
(2)①如图2,过点P作MN∥AB,则∠EPM=∠PEB(两直线平行,内错角相等).
∵AB∥CD(已知),MN∥AB(作图),
∴MN∥CD(平行于同一条直线的两条直线互相平行).
∴∠MPF=∠PFD,
∴∠EPM+∠FPM=∠PEB+∠PFD(等式的性质),
即∠EPF=∠PEB+∠PFD,
故答案为:两直线平行,内错角相等;平行于同一条直线的两条直线互相平行;∠EPM,∠MPF;
②∠EPF+∠PEB+∠PFD=360°;
证明:如图3,过作PM∥AB,
∵AB∥CD,MP∥AB,
∴MP∥CD,
∴∠BEP+∠EPM=180°,∠DFP+∠FPM=180°,
∴∠BEP+∠EPM+∠FPM+∠PFD=360°,
即∠EPF+∠PEB+∠PFD=360°;
③∠EPF+∠PFD=∠PEB.
理由:如图4,过作PM∥AB,
∵AB∥CD,MP∥AB,
∴MP∥CD,
∴∠PEB=∠MPE,∠PFD=∠MPF,
∵∠EPF+∠FPM=∠MPE,
∴∠EPF+∠PFD=∠PEB.
4.解:∵AB∥CD(已知).
∴∠A+∠ACD=180°(同旁内角已互补,两直线平行).
∵∠A=105°.
∴∠ACD=75°.
∵∠DCE=∠ACD﹣∠ACE,∠ACE=51°.
∴∠DCE=24°.
∵CD∥EF(已知).
∴∠E=∠DCE(两直线平行、内错角相等).
∴∠E=24°.
5.解:AD∥BE,理由如下:
∵AB∥CD(已知),
∴∠4=∠BAE(两直线平行,同位角相等);
∵∠3=∠4(已知),
∴∠3=∠BAE(等量代换);
∵∠1=∠2(已知),
∴∠1+∠CAF=∠2+∠CAF(等式的性质),
即∠BAF=∠DAC,
∴∠3=∠DAC(等量代换),
∴AD∥BE(内错角相等,两直线平行).
故答案为:BAE;两直线平行,同位角相等;BAE;等量代换;DAC;内错角相等,两直线平行.
6.解:(1)在图1中,∵AB∥CD,
∴∠1=∠3,
∵BE∥DF,
∴∠3=∠2,
则∠1=∠2;
在图2中,∵AB∥CD,
∴∠1=∠3,
∵BE∥DF,
∴∠2+∠3=180°,
∴∠1+∠2=180°;
故答案为:∠1=∠2、∠1+∠2=180°.
(2)根据(1)的探究过程,我们可得出结论:如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补,
故答案为:相等或互补;
(3)设一个角为x°,则另一个角为(3x﹣60)°,
分两种情况:
①x=3x﹣60,解得:x=30,
则3x﹣60=30;
②x+3x﹣60=180,解得:x=60,
则3x﹣60=120;
答:这两个角分别是30°、30°或60°、120°.
7.解:AF∥BE,
理由:
∵AB∥EF(已知)
∴∠1=∠BFE(两直线平行,内错角相等)
∵∠1=∠2(已知)
∴∠2=∠BFE(等量代换)
∵∠3=∠4(已知)
∴∠3+∠BFC=∠4+∠BFC(等式性质)
即∠AFC=∠BFE,
∴∠AFC=∠2(等量代换)
∴AF∥BE(同位角相等,两直线平行),
故答案为:∠BFE;两直线平行,内错角相等;∠2=∠BFE;等式性质;∠AFC;等量代换;同位角相等,两直线平行.
8.证明(1)∵∠1=∠2
∴AB∥EF
∴∠MAE=∠AEF=45°,且∠FEG=15°
∴∠AEG=60°
∵EG平分∠AEC
∴∠AEG=∠CEG=60°
∴∠CEF=75°
∵∠ECN=75°
∴∠FEC=∠ECN
∴EF∥CD且AB∥EF
∴AB∥CD
(2)∵∠1=∠2
∴AB∥EF
∴∠MAE+∠FEA=180°且∠MAE=140°
∴∠AEF=40°
∵∠FEG=30°
∴∠AEG=70°
∵EG平分∠AEC
∴∠GEC=∠AEG=70°
∴∠FEC=100°
∵AB∥CD,AB∥EF
∴EF∥CD
∴∠NCE+∠FEC=180°
∴∠NCE=80°
∴当∠NCE=80°时,AB∥CD
(3)∵∠1=∠2
∴AB∥EF
∴∠MAE+∠FEA=180°
∴∠FEA=180°﹣∠MAE,
∴∠AEG=∠FEA+∠FEG=180°﹣∠MAE+∠FEG
∵EG平分∠AEC
∴∠GEC=∠AEG
∴∠FEC=∠GEC+∠FEG=180°﹣∠MAE+∠FEG+∠FEG=180°﹣∠MAE+2∠FEG
∵AB∥CD,AB∥EF
∴EF∥CD
∴∠FEC+∠NCE=180°
∴180°﹣∠MAE+2∠FEG+∠NCE=180°
∴2∠FEG+∠NCE=∠MAE
∴当2∠FEG+∠NCE=∠MAE时AB∥CD
(4)∠1=∠2
∴AB∥EF
∴∠MAE+∠FEA=180°
∴∠FEA=180°﹣∠MAE,
∴∠AEG=∠FEG﹣∠FEA=∠FEG﹣180°+∠MAE
∵EG平分∠AEC
∴∠GEC=∠AEG
∴∠FEC=∠FEA+2∠AEG=180°﹣∠MAE+2∠FEG﹣360°+2∠MAE=∠MAE+2∠FEG﹣180°
∵AB∥CD,AB∥EF
∴EF∥CD
∴∠FEC+∠NCE=180°
∴∠MAE+2∠FEG﹣180°+∠NCE=180°
∴∠MAE+2∠FEG+∠NCE=360°
∴当∠MAE+2∠FEG+∠NCE=360°时,AB∥CD
9.解:(1)①∵CD∥AO,
∴∠AOE=∠D=55°,
又∵∠AOB=40°,
∴∠BOE=∠AOE﹣∠AOB=55°﹣40°=15°,
故答案为:15°;
②如图,当点E、O、D不在同一条直线上时,过F作GF∥AO,
∵CD∥AO,
∴GF∥CD,
∴∠GFE=∠D=55°,∠GFB=∠AOB=40°,
∴∠BFE=∠GFE﹣∠BFG=55°﹣40°=15°;
如图,当点E、O、D不在同一条直线上时,过F作GF∥AO,
∵CD∥AO,
∴GF∥CD,
∴∠GFE=∠D=55°,∠GFB=∠AOB=40°,
∴∠BFE=∠GFE+∠BFG=55°+40°=95°;
(2)由(1)②可得,若∠BOA=α,∠EDC=β,则∠BFE=β﹣α或β+α.
10.解:∠C与∠AED相等,理由如下:
∵∠1+∠2=180°(已知),
∠1+∠EFD=180°(邻补角定义),
∴∠2=∠EFD(等量代换),
∴AB∥EF(内错角相等,两直线平行),
∴∠3=∠ADE(两直线平行,内错角相等),
又∵∠3=∠B(已知),
∴∠B=∠ADE(等量代换),
∴DE∥BC(同位角相等,两直线平行),
∴∠C=∠AED(两直线平行,同位角相等),
故答案为:∠EFD,∠EFD,等量代换,EF,∠ADE,∠ADE,BC,∠AED.
11.解:(1)AB∥CD,
理由是:
分别过点E、F作EM∥AB,FN∥AB,
∵EM∥AB,FN∥AB,
∴EM∥FN∥AB,
∴∠1+∠A=180°,∠3+∠4=180°,
∵∠A+∠E+∠F+∠C=540°,
∴∠2+∠C=540°﹣180°﹣180°=180°,
∴FN∥CD,
∵FN∥AB,
∴AB∥CD;
(2)
设∠PAQ=x,∠PCD=y,
∵∠PAB=3∠PAQ,∠PCD=3∠PCQ,
∴∠PAB=3x,∠BAQ=2x,
∠PCD=3y,∠QCD=2y,
过P作PG∥AB,过Q作QH∥AB,
∵AB∥CD,
∴AB∥CD∥PG∥GH,
∴∠AQH=∠BAQ=2x,∠QCD=∠CQH=2y,
∴∠AQC=2x+2y=2(x+y),
同理可得:∠APC=3x+3y=3(x+y),
∴=,
即∠AQC=∠APC.
12.解:(1)∵DE平分∠ADC,∠ADC=70°,
∴∠EDC=∠ADC=×70°=35°;
(2)过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠ABE=∠BEF,∠CDE=∠DEF,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°,
∴∠ABE=∠ABC=n°,∠CDE=∠ADC=35°,
∴∠BED=∠BEF+∠DEF=n°+35°;
(3)分三种情况:
如图所示,过点E作EF∥AB,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°,
∴∠ABE=∠ABC=n°,∠CDG=∠ADC=35°,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BEF=∠ABE=n°,∠CDG=∠DEF=35°,
∴∠BED=∠BEF﹣∠DEF=n°﹣35°.
如图所示,过点E作EF∥AB,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°,
∴∠ABE=∠ABC=n°,∠CDE=∠ADC=35°,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BEF=180°﹣∠ABE=180°﹣n°,∠CDE=∠DEF=35°,
∴∠BED=∠BEF+∠DEF=180°﹣n°+35°=215°﹣n°.
如图所示,过点E作EF∥AB,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°,
∴∠ABG=∠ABC=n°,∠CDE=∠ADC=35°,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BEF=∠ABG=n°,∠CDE=∠DEF=35°,
∴∠BED=∠BEF﹣∠DEF=n°﹣35°.
综上所述,∠BED的度数为n°﹣35°或215°﹣n°.
13.解:(1)如图1,
过点P作PH∥AB∥CD
∴∠1=∠EPH,∠2=∠FPH
而∠EPF=∠EPH+∠FPH
∴∠EPF=∠1+∠2=110°;
(2)∵∠1+∠4=∠2+∠3,∠1=30°,∠2=40°,∠3=70°,
∴∠4=80°,
故答案为80°
(3)∠P1=(x+y)°(用x,y的代数式表示)
∠Pn=()n(x+y)°.
故答案为(x+y)°,()n(x+y)°.
(4)∠APB=∠C+60°.理由如下:
过A、B分别作直线AE、BF,使AE∥BF.如图,
由(1)规律可知∠C=∠1+∠2.
∠APB=∠PAE+∠PBF
=(∠PAC+∠1)+(∠PBC+∠2)
=∠PAC+∠PBC+(∠1+∠2)
=∠C+60°.
14.解:(1)如图,当P点在C、D之间运动时,则有∠APB=∠PAC+∠PBD.理由如下:
过点P作PE∥l1,
∵l1∥l2,
∴PE∥l2∥l1,
∴∠PAC=∠1,∠PBD=∠2,
∴∠APB=∠1+∠2=∠PAC+∠PBD;
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),
则有两种情形:①如图,
当点P在在l2下方时,有结论:∠APB=∠PAC﹣∠PBD.
理由是:过点P作PE∥l1,则∠APE=∠PAC,
又∵l1∥l2,
∴PE∥l2,
∴∠BPE=∠PBD,
∵∠APE=∠APB+∠BPE,
∴∠PAC=∠APB+∠PBD,
∴∠APB=∠PAC﹣∠PBD;
②如图,
当点P在l1上方时,有结论:∠APB=∠PBD﹣∠PAC.
理由是:过点P作PE∥l2,则∠BPE=∠PBD,
又∵l1∥l2,
∴PE∥l1,
∴∠APE=∠PAC,
∵∠BPE=∠APE+∠APB,
∴∠PBD=∠PAC+∠APB,
∴∠APB=∠PBD﹣∠PAC.
15.解:探究与发现:∠BDC=∠A+∠ABD+∠ACD,
理由如下:∵∠BDC+∠DBC+∠DCB=180°,
∠A+∠ABC+∠ACB=∠A+∠ABD+∠ACD+∠DBC+∠DCB=180°,
∴∠BDC=∠A+∠ABD+∠ACD,
应用:连接BC,
∵由上述结论得∠BDC=∠A+∠ABD+∠ACD=143°,
又∵由检验员量得∠BDC=145°≠143°,
∴这个零件不合格.
周末培优卷
1.如图,已知AB∥CD,点B、C、F在同一条直线上,BD平分∠ABC,CE平分∠DCF,AC⊥CE,AC与BD相交于点P,求证:AC⊥BD.
2.已知AM∥CN,点B为平面内一点,AB⊥BC于B.
(1)如图1,过点B作BD⊥AM于点D,∠BAD与∠C有何数量关系,并说明理由;
(2)如图2,在(1)问的条件下,点E,F在DM上,连接BE,BF,CF,若BF平分∠DBC,BE平分∠ABD,∠FCB+∠NCF=180°,∠BFC=5∠DBE,求∠ABE的度数.
3.已知如图,直线EF与AB、CD分别相交于点E、F.
(1)如图1,若∠1=120°,∠2=60°,求证AB∥CD;
(2)在(1)的情况下,若点P是平面内的一个动点,连结PE、PF,探索∠EPF、∠PEB、∠PFD三个角之间的关系;
①当点P在图2的位置时,可得∠EPF=∠PEB+∠PFD;
请阅读下面的解答过程,并填空(理由或数学式)
解:如图2,过点P作MN∥AB,
则∠EPM=∠PEB .
∵AB∥CD(已知),MN∥AB(作图)
∴MN∥CD .
∴∠MPF=∠PFD
∴∠ +∠ =∠PEB+∠PFD(等式的性质)
即∠EPF=∠PEB+∠PFD
②当点P在图3的位置时,∠EPF、∠PEB、∠PFD三个角之间有何关系并证明.
③当点P在图4的位置时,请直接写出∠EPF、∠PEB、∠PFD三个角之间的关系: .
4.根据下面解答过程,完成下面填空:
如图,已知AB∥CD∥EF,∠A=105°,∠ACE=51°,求∠E的度数.
5.推理填空
已知:如图所示,点B,C,E在同一条直线上,AB∥CD,∠1=∠2,∠3=∠4,求证:AD∥BE
证明:∵AB∥CD(已知)
∴∠4=∠ ( )
∵∠3=∠4(已知)∴∠3=∠ ( )
∴∠1=∠2(已知)∴∠1+∠CAF=∠2+∠CAF(等式的性质)
即∠BAF=∠DAC
∴∠3=∠ (等量代换)
∴AD∥BE( )
6.如果一个角的两边与另一个角的两边分别平行,某同学为了探究这两个角之间的关系,画出了以下两个不同的图形,请你根据图形完成以下问题:
(1)如图①,如果AB∥CD,BE∥DF,那么∠1与∠2的关系是 ;
如图②,如果AB∥CD,BE∥DF,那么∠1与∠2的关系是 .
(2)根据(1)的探究过程,我们可得出结论:如果一个角的两边与另一个角的两边分别平行,那么这两个角 ;
(3)利用结论解决问题:如果有两个角的两边分别平行,且一个角比另一个角的3倍少60°,则这两个角分别是多少度?
7.完成下面证明
已知,如图,AB∥EF,∠1=∠2,∠3=∠4,AF与BE平行吗?为什么?
解:AF∥BE
理由:
∵AB∥EF(已知)
∴∠1= ( )
∠1=∠2(已知)
∴ (等量代换)
∵∠3=∠4(已知
∴∠3+∠BFC=∠4+∠BFC( )
即∠AFC=∠BFE
∴ =∠2( )
∴AF∥BE( )
8.已知:∠1=∠2,EG平分∠AEC.
(1)如图①,∠MAE=45°,∠FEG=15°,∠NCE=75°.求证:AB∥CD;
(2)如图②,∠MAE=140°,∠FEG=30°,当∠NCE= °时,AB∥CD;
(3)如图②,请你直接写出∠MAE、∠FEG、∠NCE之间满足什么关系时,AB∥CD;
(4)如图③,请你直接写出∠MAE、∠FEG、∠NCE之间满足什么关系时,AB∥CD.
9.有两个∠AOB与∠EDC,∠EDC保持不动,且∠EDC的一边CD∥AO,另一边DE与直线OB相交于点F.
(1)若∠AOB=40°,∠EDC=55°,解答下列问题:
①如图,当点E、O、D在同一条直线上,即点O与点F重合,则∠BOE= ;
②当点E、O、D不在同一条直线上,画出图形并求∠BFE的度数;
(2)在(1)②的前提下,若∠AOB=α,∠EDC=β,且α<β,请直接写出∠BFE的度数(用含α、β的式子表示).
10.如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并证明你的结论.
解:∠C与∠AED相等,理由如下:
∵∠1+∠2=180°(已知)
∠1+ =180°(邻补角定义)
∴∠2= ( )
∴AB∥ (内错角相等,两直线平行)
∴∠3= (两直线平行,内错角相等)
又∵∠3=∠B(已知)
∴∠B= (等量代换)
∴DE∥ (同位角相等,两直线平行)
∴∠C= (两直线平行,同位角相等)
11.如图1,已知∠A+∠E+∠F+∠C=540°.
(1)试判断直线AB与CD的位置关系,并说明理由
(2)如图2,∠PAB=3∠PAQ,∠PCD=3∠PCQ,试判断∠APC与∠AQC的数量关系,并说明理由.
12.如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E.∠ADC=70°.
(1)求∠EDC的度数;
(2)若∠ABC=n°,求∠BED的度数(用含n的式子表示);
(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示),不改变,请说明理由.
13.如图1,直线AB∥CD,点P在两平行线之间,点E在AB上,点F在CD上,连结PE,PF.
(1)若∠PEB=60°,∠PFD=50°,请求出∠EPF.(请写出必要的步骤说明理由)
(2)如图2,若点P、Q在直线AB与CD之间时,∠1=30°,∠2=40°,∠3=70°,请求出∠P4= .(不需说明理由,请直接写出答案)
(3)如图3,作P1E平分∠PEB,P1F平分∠PFD,若设∠PEB=x°,∠PFD=y°则∠EP1F= (用x、y的代数式表示),若P2E平分∠P1EB,P2F平分∠P1FD,可得∠EP2F;P3E平分∠P2EB,P3F平分∠P2FD,可得∠EP3F,依次平分下去,则∠EPnF= .
(4)在一次综合实践活动课上,张开同学制作了一个图5的“回旋镖“,经测量发现∠PAC=38°,∠PBC=22°,请你找出∠APB与∠C的数量关系并说明理由
14.如图,已知直线l1∥l2,点A、B分别在l1与l2上.直线l3和直线l1、l2交于点C和D,在直线CD上有一点P.
(1)如果P点在C、D之间运动时,问∠PAC,∠APB,∠PBD有怎样的数量关系?请说明理由.
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?
15.探究与发现:有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C.请写出∠BDC与∠A+∠ABD+∠ACD之间的数量关系,并说明理由.
应用:某零件如图所示,图纸要求∠A=90°,∠B=32°,∠C=21°,当检验员量得∠BDC=145°,就断定这个零件不合格,你能说出其中的道理吗?
参考答案
1.证明:∵AB∥CD,
∴∠ABC=∠DCF,
∵BD平分∠ABC,CE平分∠DCF,
∴∠1=∠2=∠3=∠4,
∵AC⊥CE,
∴∠4+∠PCB=90°,
∴∠2+∠PCB=90°,
∴∠BPC=90°,
∴AC⊥BD.
2.解:(1)如图1,过点B作BG∥DM,
∵BD⊥AM,
∴∠ABD+∠BAD=90°,DB⊥BG,即∠ABD+∠ABG=90°,
又∵AB⊥BC,
∴∠CBG+∠ABG=90°,
∴∠ABD=∠CBG,
∵AM∥CN,BG∥AM,
∴CN∥BG,
∴∠C=∠CBG,
∴∠ABD=∠C,
∴∠C+∠BAD=90°;
(2)如图2,过点B作BG∥DM,
∵BF平分∠DBC,BE平分∠ABD,
∴∠DBF=∠CBF,∠DBE=∠ABE,
由(1)可得∠ABD=∠CBG,
∴∠ABF=∠GBF,
设∠DBE=α,∠ABF=β,则
∠ABE=α,∠ABD=2α=∠CBG,∠GBF=β=∠AFB,∠BFC=5∠DBE=5α,
∴∠AFC=5α+β,
∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,
∴∠FCB=∠AFC=5α+β,
△BCF中,由∠CBF+∠BFC+∠BCF=180°,可得
(2α+β)+5α+(5α+β)=180°,①
由AB⊥BC,可得
β+β+2α=90°,②
由①②联立方程组,解得α=9°,
∴∠ABE=9°.
3.解:(1)∵∠1=120°,
∴∠BEF=120°,
又∵∠2=60°,
∴∠2+∠BEF=180°,
∴AB∥CD;
(2)①如图2,过点P作MN∥AB,则∠EPM=∠PEB(两直线平行,内错角相等).
∵AB∥CD(已知),MN∥AB(作图),
∴MN∥CD(平行于同一条直线的两条直线互相平行).
∴∠MPF=∠PFD,
∴∠EPM+∠FPM=∠PEB+∠PFD(等式的性质),
即∠EPF=∠PEB+∠PFD,
故答案为:两直线平行,内错角相等;平行于同一条直线的两条直线互相平行;∠EPM,∠MPF;
②∠EPF+∠PEB+∠PFD=360°;
证明:如图3,过作PM∥AB,
∵AB∥CD,MP∥AB,
∴MP∥CD,
∴∠BEP+∠EPM=180°,∠DFP+∠FPM=180°,
∴∠BEP+∠EPM+∠FPM+∠PFD=360°,
即∠EPF+∠PEB+∠PFD=360°;
③∠EPF+∠PFD=∠PEB.
理由:如图4,过作PM∥AB,
∵AB∥CD,MP∥AB,
∴MP∥CD,
∴∠PEB=∠MPE,∠PFD=∠MPF,
∵∠EPF+∠FPM=∠MPE,
∴∠EPF+∠PFD=∠PEB.
4.解:∵AB∥CD(已知).
∴∠A+∠ACD=180°(同旁内角已互补,两直线平行).
∵∠A=105°.
∴∠ACD=75°.
∵∠DCE=∠ACD﹣∠ACE,∠ACE=51°.
∴∠DCE=24°.
∵CD∥EF(已知).
∴∠E=∠DCE(两直线平行、内错角相等).
∴∠E=24°.
5.解:AD∥BE,理由如下:
∵AB∥CD(已知),
∴∠4=∠BAE(两直线平行,同位角相等);
∵∠3=∠4(已知),
∴∠3=∠BAE(等量代换);
∵∠1=∠2(已知),
∴∠1+∠CAF=∠2+∠CAF(等式的性质),
即∠BAF=∠DAC,
∴∠3=∠DAC(等量代换),
∴AD∥BE(内错角相等,两直线平行).
故答案为:BAE;两直线平行,同位角相等;BAE;等量代换;DAC;内错角相等,两直线平行.
6.解:(1)在图1中,∵AB∥CD,
∴∠1=∠3,
∵BE∥DF,
∴∠3=∠2,
则∠1=∠2;
在图2中,∵AB∥CD,
∴∠1=∠3,
∵BE∥DF,
∴∠2+∠3=180°,
∴∠1+∠2=180°;
故答案为:∠1=∠2、∠1+∠2=180°.
(2)根据(1)的探究过程,我们可得出结论:如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补,
故答案为:相等或互补;
(3)设一个角为x°,则另一个角为(3x﹣60)°,
分两种情况:
①x=3x﹣60,解得:x=30,
则3x﹣60=30;
②x+3x﹣60=180,解得:x=60,
则3x﹣60=120;
答:这两个角分别是30°、30°或60°、120°.
7.解:AF∥BE,
理由:
∵AB∥EF(已知)
∴∠1=∠BFE(两直线平行,内错角相等)
∵∠1=∠2(已知)
∴∠2=∠BFE(等量代换)
∵∠3=∠4(已知)
∴∠3+∠BFC=∠4+∠BFC(等式性质)
即∠AFC=∠BFE,
∴∠AFC=∠2(等量代换)
∴AF∥BE(同位角相等,两直线平行),
故答案为:∠BFE;两直线平行,内错角相等;∠2=∠BFE;等式性质;∠AFC;等量代换;同位角相等,两直线平行.
8.证明(1)∵∠1=∠2
∴AB∥EF
∴∠MAE=∠AEF=45°,且∠FEG=15°
∴∠AEG=60°
∵EG平分∠AEC
∴∠AEG=∠CEG=60°
∴∠CEF=75°
∵∠ECN=75°
∴∠FEC=∠ECN
∴EF∥CD且AB∥EF
∴AB∥CD
(2)∵∠1=∠2
∴AB∥EF
∴∠MAE+∠FEA=180°且∠MAE=140°
∴∠AEF=40°
∵∠FEG=30°
∴∠AEG=70°
∵EG平分∠AEC
∴∠GEC=∠AEG=70°
∴∠FEC=100°
∵AB∥CD,AB∥EF
∴EF∥CD
∴∠NCE+∠FEC=180°
∴∠NCE=80°
∴当∠NCE=80°时,AB∥CD
(3)∵∠1=∠2
∴AB∥EF
∴∠MAE+∠FEA=180°
∴∠FEA=180°﹣∠MAE,
∴∠AEG=∠FEA+∠FEG=180°﹣∠MAE+∠FEG
∵EG平分∠AEC
∴∠GEC=∠AEG
∴∠FEC=∠GEC+∠FEG=180°﹣∠MAE+∠FEG+∠FEG=180°﹣∠MAE+2∠FEG
∵AB∥CD,AB∥EF
∴EF∥CD
∴∠FEC+∠NCE=180°
∴180°﹣∠MAE+2∠FEG+∠NCE=180°
∴2∠FEG+∠NCE=∠MAE
∴当2∠FEG+∠NCE=∠MAE时AB∥CD
(4)∠1=∠2
∴AB∥EF
∴∠MAE+∠FEA=180°
∴∠FEA=180°﹣∠MAE,
∴∠AEG=∠FEG﹣∠FEA=∠FEG﹣180°+∠MAE
∵EG平分∠AEC
∴∠GEC=∠AEG
∴∠FEC=∠FEA+2∠AEG=180°﹣∠MAE+2∠FEG﹣360°+2∠MAE=∠MAE+2∠FEG﹣180°
∵AB∥CD,AB∥EF
∴EF∥CD
∴∠FEC+∠NCE=180°
∴∠MAE+2∠FEG﹣180°+∠NCE=180°
∴∠MAE+2∠FEG+∠NCE=360°
∴当∠MAE+2∠FEG+∠NCE=360°时,AB∥CD
9.解:(1)①∵CD∥AO,
∴∠AOE=∠D=55°,
又∵∠AOB=40°,
∴∠BOE=∠AOE﹣∠AOB=55°﹣40°=15°,
故答案为:15°;
②如图,当点E、O、D不在同一条直线上时,过F作GF∥AO,
∵CD∥AO,
∴GF∥CD,
∴∠GFE=∠D=55°,∠GFB=∠AOB=40°,
∴∠BFE=∠GFE﹣∠BFG=55°﹣40°=15°;
如图,当点E、O、D不在同一条直线上时,过F作GF∥AO,
∵CD∥AO,
∴GF∥CD,
∴∠GFE=∠D=55°,∠GFB=∠AOB=40°,
∴∠BFE=∠GFE+∠BFG=55°+40°=95°;
(2)由(1)②可得,若∠BOA=α,∠EDC=β,则∠BFE=β﹣α或β+α.
10.解:∠C与∠AED相等,理由如下:
∵∠1+∠2=180°(已知),
∠1+∠EFD=180°(邻补角定义),
∴∠2=∠EFD(等量代换),
∴AB∥EF(内错角相等,两直线平行),
∴∠3=∠ADE(两直线平行,内错角相等),
又∵∠3=∠B(已知),
∴∠B=∠ADE(等量代换),
∴DE∥BC(同位角相等,两直线平行),
∴∠C=∠AED(两直线平行,同位角相等),
故答案为:∠EFD,∠EFD,等量代换,EF,∠ADE,∠ADE,BC,∠AED.
11.解:(1)AB∥CD,
理由是:
分别过点E、F作EM∥AB,FN∥AB,
∵EM∥AB,FN∥AB,
∴EM∥FN∥AB,
∴∠1+∠A=180°,∠3+∠4=180°,
∵∠A+∠E+∠F+∠C=540°,
∴∠2+∠C=540°﹣180°﹣180°=180°,
∴FN∥CD,
∵FN∥AB,
∴AB∥CD;
(2)
设∠PAQ=x,∠PCD=y,
∵∠PAB=3∠PAQ,∠PCD=3∠PCQ,
∴∠PAB=3x,∠BAQ=2x,
∠PCD=3y,∠QCD=2y,
过P作PG∥AB,过Q作QH∥AB,
∵AB∥CD,
∴AB∥CD∥PG∥GH,
∴∠AQH=∠BAQ=2x,∠QCD=∠CQH=2y,
∴∠AQC=2x+2y=2(x+y),
同理可得:∠APC=3x+3y=3(x+y),
∴=,
即∠AQC=∠APC.
12.解:(1)∵DE平分∠ADC,∠ADC=70°,
∴∠EDC=∠ADC=×70°=35°;
(2)过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠ABE=∠BEF,∠CDE=∠DEF,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°,
∴∠ABE=∠ABC=n°,∠CDE=∠ADC=35°,
∴∠BED=∠BEF+∠DEF=n°+35°;
(3)分三种情况:
如图所示,过点E作EF∥AB,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°,
∴∠ABE=∠ABC=n°,∠CDG=∠ADC=35°,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BEF=∠ABE=n°,∠CDG=∠DEF=35°,
∴∠BED=∠BEF﹣∠DEF=n°﹣35°.
如图所示,过点E作EF∥AB,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°,
∴∠ABE=∠ABC=n°,∠CDE=∠ADC=35°,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BEF=180°﹣∠ABE=180°﹣n°,∠CDE=∠DEF=35°,
∴∠BED=∠BEF+∠DEF=180°﹣n°+35°=215°﹣n°.
如图所示,过点E作EF∥AB,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°,
∴∠ABG=∠ABC=n°,∠CDE=∠ADC=35°,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BEF=∠ABG=n°,∠CDE=∠DEF=35°,
∴∠BED=∠BEF﹣∠DEF=n°﹣35°.
综上所述,∠BED的度数为n°﹣35°或215°﹣n°.
13.解:(1)如图1,
过点P作PH∥AB∥CD
∴∠1=∠EPH,∠2=∠FPH
而∠EPF=∠EPH+∠FPH
∴∠EPF=∠1+∠2=110°;
(2)∵∠1+∠4=∠2+∠3,∠1=30°,∠2=40°,∠3=70°,
∴∠4=80°,
故答案为80°
(3)∠P1=(x+y)°(用x,y的代数式表示)
∠Pn=()n(x+y)°.
故答案为(x+y)°,()n(x+y)°.
(4)∠APB=∠C+60°.理由如下:
过A、B分别作直线AE、BF,使AE∥BF.如图,
由(1)规律可知∠C=∠1+∠2.
∠APB=∠PAE+∠PBF
=(∠PAC+∠1)+(∠PBC+∠2)
=∠PAC+∠PBC+(∠1+∠2)
=∠C+60°.
14.解:(1)如图,当P点在C、D之间运动时,则有∠APB=∠PAC+∠PBD.理由如下:
过点P作PE∥l1,
∵l1∥l2,
∴PE∥l2∥l1,
∴∠PAC=∠1,∠PBD=∠2,
∴∠APB=∠1+∠2=∠PAC+∠PBD;
(2)若点P在C、D两点的外侧运动时(P点与点C、D不重合),
则有两种情形:①如图,
当点P在在l2下方时,有结论:∠APB=∠PAC﹣∠PBD.
理由是:过点P作PE∥l1,则∠APE=∠PAC,
又∵l1∥l2,
∴PE∥l2,
∴∠BPE=∠PBD,
∵∠APE=∠APB+∠BPE,
∴∠PAC=∠APB+∠PBD,
∴∠APB=∠PAC﹣∠PBD;
②如图,
当点P在l1上方时,有结论:∠APB=∠PBD﹣∠PAC.
理由是:过点P作PE∥l2,则∠BPE=∠PBD,
又∵l1∥l2,
∴PE∥l1,
∴∠APE=∠PAC,
∵∠BPE=∠APE+∠APB,
∴∠PBD=∠PAC+∠APB,
∴∠APB=∠PBD﹣∠PAC.
15.解:探究与发现:∠BDC=∠A+∠ABD+∠ACD,
理由如下:∵∠BDC+∠DBC+∠DCB=180°,
∠A+∠ABC+∠ACB=∠A+∠ABD+∠ACD+∠DBC+∠DCB=180°,
∴∠BDC=∠A+∠ABD+∠ACD,
应用:连接BC,
∵由上述结论得∠BDC=∠A+∠ABD+∠ACD=143°,
又∵由检验员量得∠BDC=145°≠143°,
∴这个零件不合格.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
