《分类计数原理与分步计数原理》课件
文档属性
| 名称 | 《分类计数原理与分步计数原理》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 257.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-13 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
第十章 排列、组合 和二项式定理
贵阳市民族中学 杜旭林
32
支
球
队
4支球队
4支球队
4支球队
4支球队
4支球队
4支球队
4支球队
4支球队
4支球队
4支球队
4支球队
4支球队
4支球队
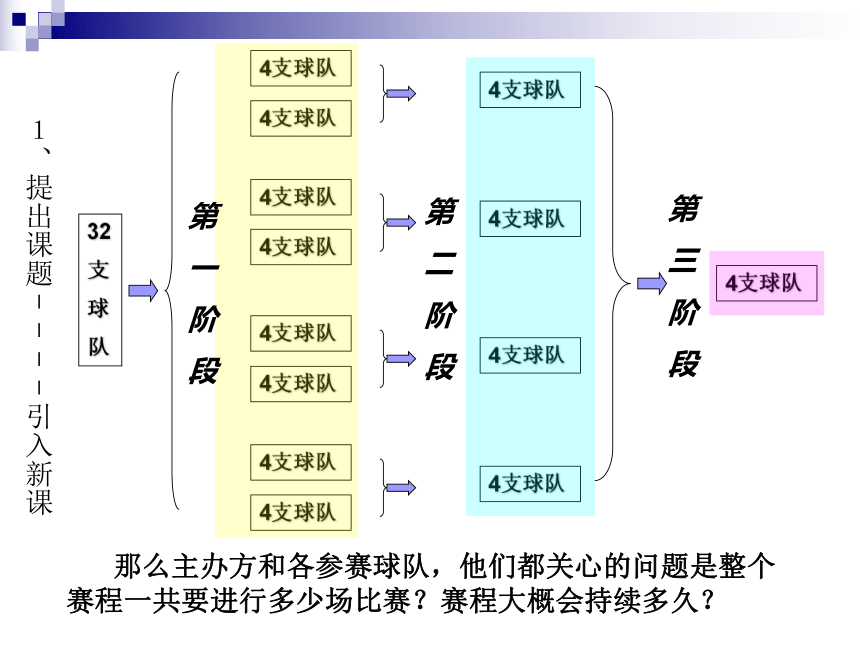
那么主办方和各参赛球队,他们都关心的问题是整个赛程一共要进行多少场比赛?赛程大概会持续多久?
第
一
阶
段
第
二
阶
段
第
三
阶
段
1、提出课题----引入新课
10.1 分类计数原理与分步计数原理
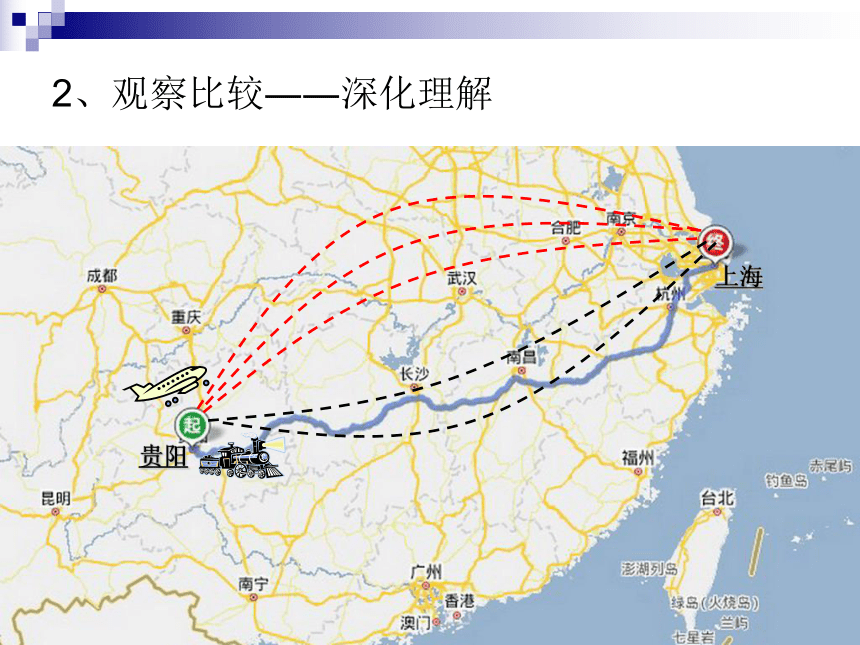
2、观察比较――深化理解
探究问题1:
我校要派出部分老师到上海参观、培训,可以乘飞机,也可以乘火车。一天中,飞机有3班,火车有2班。那么一天中,乘坐这些交通工具从贵阳到上海共有多少种不同的走法?
贵阳
上海
2、观察比较――深化理解
2、观察比较――深化理解
分类计数原理:
完成一件事,有n类办法,在第1类办法中有m1种不同的方法,在第2类办法中有m2种不同的方法……在第n类办法中有mn种不同的方法,那么完成这件事共有:
N=m1+m2+ +mn
种不同的方法。
2、观察比较――深化理解
探究问题2:
我校要派出部分老师到上海参观、培训,要从贵阳先乘飞机到长沙,再于次日从长沙乘火车到上海.一天中,飞机有3班,火车有2班.那么两天中,从贵阳到上海共有多少种不同的走法?
贵阳
上海
长沙
2、观察比较――深化理解
飞机3——火车1
飞机3——火车2
飞机2——火车1
飞机2——火车2
飞机1——火车1
飞机1——火车2
所有走法:
2、观察比较――深化理解
分步计数原理:
完成一件事,需要分成n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法……做第n步有mn种不同的方法,那么完成这件事共有:
N=m1×m2 × × mn
种不同的方法.
能否独立完成一件事,是判断分类或分步的依据.
特别说明
每一步不能独立完成这件事,只有各个步骤都完成才算完成这件事.
每一类办法都能独立完成这件事.
分类法:
分步法:
区 别
回答的都是有关做一件事的不同方法的种数的问题.
相 同 点
请大家思考:两个原理之间的有什么联系与区别?
2、观察比较――深化理解
3、学以致用----培养能力
例1.书架的第一层放有4本不同的计算书,
第二层放有3本不同的文艺书,第3层放有
2本不同的体育书.
(1)从书架上任取1本书,有多
少种不同的取法?
(2)从书架的第1、2、3层各取
1本书,有多少种不同的取法?
3、学以致用----培养能力
例2.一种号码锁有4个拨号盘,每个拨号盘上有从0到9共10个数字,这4个拨号盘可以组成多少个四位数字的号码
解:由于号码锁的每个拨号盘有从0到9这10个数字,每个拨号盘上的数字有10种取法.根据分步计数原理,4个拨号盘上各取一个数字组成的四位数字号码的个数是
N=10×10×10×10=10000.
答:可以组成10000个四位数字号码.
3、学以致用----培养能力
例3.如图,从甲地到乙地有2条路,从乙地到丁地有3条路;从甲地到丙地有4条路,从丙地到丁地有2条路.从甲地到丁地共有多少种不同的走法?
解:从甲地到丁地,有两类走法:第一类走法(甲经乙到丁)有:2×3=6种走法;第二类走法(甲经丙到丁)有:4×2=8种走法;
所以从甲地到丁地共有:6+8=14种走法。
4、任务后延----自主探究
(1)填空:
①一件工作可以用2种方法完成,有5人会第一种方法完成,另有4人会用第2种方法完成,从中选出1人来完成这件工作,不同的选法的种数是 _____.
9
6
②从A村去B村的道路有3条,从B村去C村的道路有2条,从A村经B村去C村,不同走法的种数是_____
4、任务后延----自主探究
(2)现有高中一年级的学生3名,高中二年级的学生5名,高中三年级的学生4名.
①从中选1人参加接待外宾的活动,有多少种不同的选法?
②从3个年级的学生中各选1人参加接待外宾的活动,有多少种不同的选法?
③从3个年级的学生中选出2人参加接待外宾的活动,要求这2人来自不同年级, 有多少种不同的选法?
5、总结反思----提高认识
本节课学习了以下内容
(1)学习了两个原理:
分类计数原理与分步计数原理;
(2)理解了两个原理的联系与区别;
(3)分析了用两个原理解题的步骤,体会了
解决实际问题的两种思想.
6、布置作业----知识拓展
P97 习题 10.1
1, 3 题
再见
第十章 排列、组合 和二项式定理
贵阳市民族中学 杜旭林
32
支
球
队
4支球队
4支球队
4支球队
4支球队
4支球队
4支球队
4支球队
4支球队
4支球队
4支球队
4支球队
4支球队
4支球队
那么主办方和各参赛球队,他们都关心的问题是整个赛程一共要进行多少场比赛?赛程大概会持续多久?
第
一
阶
段
第
二
阶
段
第
三
阶
段
1、提出课题----引入新课
10.1 分类计数原理与分步计数原理
2、观察比较――深化理解
探究问题1:
我校要派出部分老师到上海参观、培训,可以乘飞机,也可以乘火车。一天中,飞机有3班,火车有2班。那么一天中,乘坐这些交通工具从贵阳到上海共有多少种不同的走法?
贵阳
上海
2、观察比较――深化理解
2、观察比较――深化理解
分类计数原理:
完成一件事,有n类办法,在第1类办法中有m1种不同的方法,在第2类办法中有m2种不同的方法……在第n类办法中有mn种不同的方法,那么完成这件事共有:
N=m1+m2+ +mn
种不同的方法。
2、观察比较――深化理解
探究问题2:
我校要派出部分老师到上海参观、培训,要从贵阳先乘飞机到长沙,再于次日从长沙乘火车到上海.一天中,飞机有3班,火车有2班.那么两天中,从贵阳到上海共有多少种不同的走法?
贵阳
上海
长沙
2、观察比较――深化理解
飞机3——火车1
飞机3——火车2
飞机2——火车1
飞机2——火车2
飞机1——火车1
飞机1——火车2
所有走法:
2、观察比较――深化理解
分步计数原理:
完成一件事,需要分成n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法……做第n步有mn种不同的方法,那么完成这件事共有:
N=m1×m2 × × mn
种不同的方法.
能否独立完成一件事,是判断分类或分步的依据.
特别说明
每一步不能独立完成这件事,只有各个步骤都完成才算完成这件事.
每一类办法都能独立完成这件事.
分类法:
分步法:
区 别
回答的都是有关做一件事的不同方法的种数的问题.
相 同 点
请大家思考:两个原理之间的有什么联系与区别?
2、观察比较――深化理解
3、学以致用----培养能力
例1.书架的第一层放有4本不同的计算书,
第二层放有3本不同的文艺书,第3层放有
2本不同的体育书.
(1)从书架上任取1本书,有多
少种不同的取法?
(2)从书架的第1、2、3层各取
1本书,有多少种不同的取法?
3、学以致用----培养能力
例2.一种号码锁有4个拨号盘,每个拨号盘上有从0到9共10个数字,这4个拨号盘可以组成多少个四位数字的号码
解:由于号码锁的每个拨号盘有从0到9这10个数字,每个拨号盘上的数字有10种取法.根据分步计数原理,4个拨号盘上各取一个数字组成的四位数字号码的个数是
N=10×10×10×10=10000.
答:可以组成10000个四位数字号码.
3、学以致用----培养能力
例3.如图,从甲地到乙地有2条路,从乙地到丁地有3条路;从甲地到丙地有4条路,从丙地到丁地有2条路.从甲地到丁地共有多少种不同的走法?
解:从甲地到丁地,有两类走法:第一类走法(甲经乙到丁)有:2×3=6种走法;第二类走法(甲经丙到丁)有:4×2=8种走法;
所以从甲地到丁地共有:6+8=14种走法。
4、任务后延----自主探究
(1)填空:
①一件工作可以用2种方法完成,有5人会第一种方法完成,另有4人会用第2种方法完成,从中选出1人来完成这件工作,不同的选法的种数是 _____.
9
6
②从A村去B村的道路有3条,从B村去C村的道路有2条,从A村经B村去C村,不同走法的种数是_____
4、任务后延----自主探究
(2)现有高中一年级的学生3名,高中二年级的学生5名,高中三年级的学生4名.
①从中选1人参加接待外宾的活动,有多少种不同的选法?
②从3个年级的学生中各选1人参加接待外宾的活动,有多少种不同的选法?
③从3个年级的学生中选出2人参加接待外宾的活动,要求这2人来自不同年级, 有多少种不同的选法?
5、总结反思----提高认识
本节课学习了以下内容
(1)学习了两个原理:
分类计数原理与分步计数原理;
(2)理解了两个原理的联系与区别;
(3)分析了用两个原理解题的步骤,体会了
解决实际问题的两种思想.
6、布置作业----知识拓展
P97 习题 10.1
1, 3 题
再见
