高中数学人教A必修一课件-1.1.4集合复习课(19张PPT)
文档属性
| 名称 | 高中数学人教A必修一课件-1.1.4集合复习课(19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-13 12:29:40 | ||
图片预览






文档简介
集合复习课
要点·疑点·考点
二、元素与集合、集合与集合之间的关系
一、集合的基本概念及表示方法
三、集合之间的运算性质
四、有限集合的子集个数
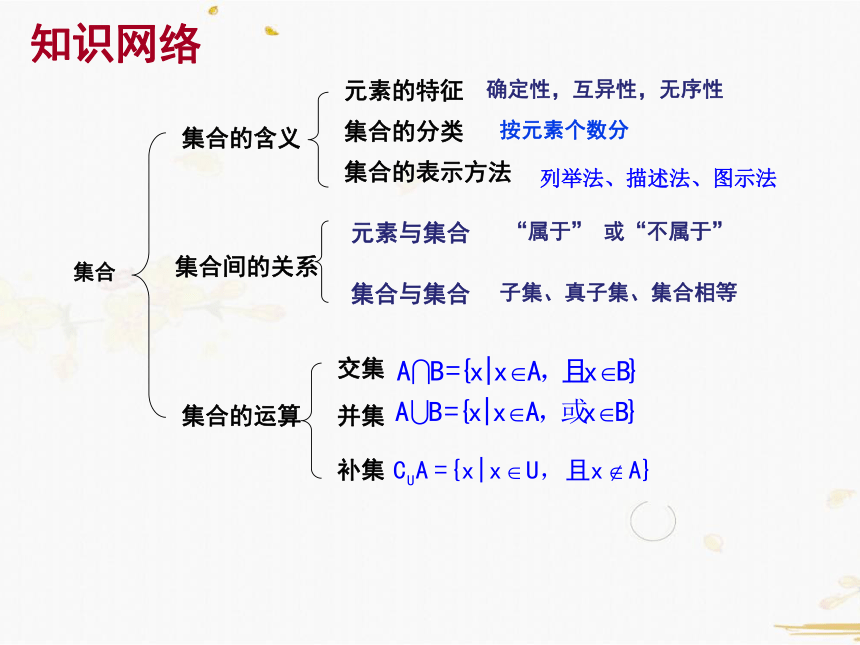
知识网络
集合
集合的含义
元素的特征
集合的分类
集合的表示方法
集合间的关系
元素与集合
集合与集合
集合的运算
交集
并集
补集
确定性,互异性,无序性
列举法、描述法、图示法
“属于” 或“不属于”
子集、真子集、集合相等
按元素个数分
集合之间的运算性质
1.交集的运算性质
A∩B=B∩A,A∩B A,A∩B B,A∩A=A,A∩Φ=Φ,A B?A∩B=A
2.并集的运算性质
A∪B=B∪A,A∪B A,A∪B B,A∪A=A,A∪Φ=A,A B?A∪B=B
3.补集的运算的性质
Cu(CuA)=A,CuΦ=u,A∩CuA=Φ,A∪CuA=S
Cu (A∩B)=(CuA)∪(CuB),Cu (A∪B)=(CuA)∩(CuB)
1. 设有限集合A中有n个元素,其中真子集的个数为2n-1个,非空子集个数为2n-1个,非空真子集个数为2n-2个
2. 对任意两个有限集合A、B有
card(A∪B)=card(A)+card(B)-card(A∩B)
有限集合的子集个数公式
A
题型1:
集合概念的理解及元素的特性
B
特别提示:解答集合问题,必须准确理解集合的有关
概念,对于用描述法给出的集合 ,
要紧紧抓住竖线前面的代表x以及它所具有
的 性质P,例如:
特别提示:解答集合问题,必须准确理解集合的有关
概念,对于用描述法给出的集合 ,
要紧紧抓住竖线前面的代表x以及它所具有
的 性质P,例如:
A
关键:验证求出的集合是否满足“互异性”
练习2:
集合 A = { x│ax2 +2x+1=0}中有且只有一个元素,求 a 的值 .
题型2:
子集与真子集的概念
A
B
特别提示:
(1)空集是任何集合的子集;是任何非空集合的真子集
(2)任何集合都是它本身的子集
等价转化思想
分类讨论
引申:
题型3
集合的运算
C
数形结合的思想
数轴法
1.已知集合 集合
则M∩N是( )
(A) (B) { 1 }
(C) {1,4} (D) Φ
B
练习:
2.集合S,M,N,P如图所示,则图中阴影部分所
表示的集合是( )
(A) M∩(N∪P)
(B) M∩CS(N∩P)
(C) M∪CS(N∩P)
(D) M∩CS(N∪P)
D
空集优先原则
题型4
集合实际应用
例4:高一某班的学生中,参加语文课外小组的有20人,参加数学课外小组的有22人,既参加语文又参加数学小组的有10人,既未参加语文又未参加数学小组的有15人,问该班共有学生多少人?
分析:
画出韦恩图,形象地表示出各数量关系的联系
语文
数学
方法归纳:
解决这一类问题一般借用数形结合,借助于Venn 图,把抽象的数学语言与直观的图形结合起来
小结:
(1)基本概念的理解与掌握
(2)体会分类讨论,等价转化,
数形结合思想
要点·疑点·考点
二、元素与集合、集合与集合之间的关系
一、集合的基本概念及表示方法
三、集合之间的运算性质
四、有限集合的子集个数
知识网络
集合
集合的含义
元素的特征
集合的分类
集合的表示方法
集合间的关系
元素与集合
集合与集合
集合的运算
交集
并集
补集
确定性,互异性,无序性
列举法、描述法、图示法
“属于” 或“不属于”
子集、真子集、集合相等
按元素个数分
集合之间的运算性质
1.交集的运算性质
A∩B=B∩A,A∩B A,A∩B B,A∩A=A,A∩Φ=Φ,A B?A∩B=A
2.并集的运算性质
A∪B=B∪A,A∪B A,A∪B B,A∪A=A,A∪Φ=A,A B?A∪B=B
3.补集的运算的性质
Cu(CuA)=A,CuΦ=u,A∩CuA=Φ,A∪CuA=S
Cu (A∩B)=(CuA)∪(CuB),Cu (A∪B)=(CuA)∩(CuB)
1. 设有限集合A中有n个元素,其中真子集的个数为2n-1个,非空子集个数为2n-1个,非空真子集个数为2n-2个
2. 对任意两个有限集合A、B有
card(A∪B)=card(A)+card(B)-card(A∩B)
有限集合的子集个数公式
A
题型1:
集合概念的理解及元素的特性
B
特别提示:解答集合问题,必须准确理解集合的有关
概念,对于用描述法给出的集合 ,
要紧紧抓住竖线前面的代表x以及它所具有
的 性质P,例如:
特别提示:解答集合问题,必须准确理解集合的有关
概念,对于用描述法给出的集合 ,
要紧紧抓住竖线前面的代表x以及它所具有
的 性质P,例如:
A
关键:验证求出的集合是否满足“互异性”
练习2:
集合 A = { x│ax2 +2x+1=0}中有且只有一个元素,求 a 的值 .
题型2:
子集与真子集的概念
A
B
特别提示:
(1)空集是任何集合的子集;是任何非空集合的真子集
(2)任何集合都是它本身的子集
等价转化思想
分类讨论
引申:
题型3
集合的运算
C
数形结合的思想
数轴法
1.已知集合 集合
则M∩N是( )
(A) (B) { 1 }
(C) {1,4} (D) Φ
B
练习:
2.集合S,M,N,P如图所示,则图中阴影部分所
表示的集合是( )
(A) M∩(N∪P)
(B) M∩CS(N∩P)
(C) M∪CS(N∩P)
(D) M∩CS(N∪P)
D
空集优先原则
题型4
集合实际应用
例4:高一某班的学生中,参加语文课外小组的有20人,参加数学课外小组的有22人,既参加语文又参加数学小组的有10人,既未参加语文又未参加数学小组的有15人,问该班共有学生多少人?
分析:
画出韦恩图,形象地表示出各数量关系的联系
语文
数学
方法归纳:
解决这一类问题一般借用数形结合,借助于Venn 图,把抽象的数学语言与直观的图形结合起来
小结:
(1)基本概念的理解与掌握
(2)体会分类讨论,等价转化,
数形结合思想
