高中数学人教A必修一课件-3.2函数模型及其应用(19张PPT)
文档属性
| 名称 | 高中数学人教A必修一课件-3.2函数模型及其应用(19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 710.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-13 12:42:00 | ||
图片预览






文档简介
3.2函数模型及其应用
函数是描述客观世界变化规律的基本数学模型,不同的变化规律需要不同的函数模型来描述的,我们学过的函数模型有哪些呢?
一次函数 二次函数 指数函数 对数函数 幂函数 等等
对于实际问题,我们如何选择一个恰当的函数模型来刻画它呢?找出模型后又是如何去研究它的性质呢?
例1 、 假设你有一笔资金用于投资,现在有三种投资方案供你选择,这三种方案的回报如下:
方案一、每天回报40元;
方案二、第一天回报10元,以后每天比前一天多回报10元;
方案三、第一天回报0.4元,以后每天的回报比前一天翻一番。
请问,你会选择哪种投资方案?
我们可以先建立三种投资方案所对应的函数模型,再通过比较它们的增长情况,为选择投资方案提供依据。
解:设第x天所得回报为y元,则
方案一:每天回报40元; y=40 (x∈N*)
方案二:第一天回报10元,以后每天比前一天多回 报10元; y=10x (x∈N*)
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番。
y=0.4×2x-1 (x∈N*)
投资方案选择原则:
投入资金相同,回报量多者为优
(1)比较三种方案每天回报量
(2)比较三种方案一段时间内的总回报量
哪个方案在某段时间内的总回报量最多,我们就在那段时间选择该方案。
(3)三个函数模型的增减性如何?
(4)要对三个方案作出选择,就要对它们的增长情况进行分析,如何分析?
x/天
方案一
方案二
方案三
y/元
增长量/元
y/元
增长量/元
y/元
增长量/元
1
40
10
0.4
2
40
0
20
10
0.8
0.4
3
40
0
30
10
1.6
0.8
4
40
0
40
10
3.2
1.6
5
40
0
50
10
6.4
3.2
6
40
0
60
10
12.8
6.4
7
40
0
70
10
25.6
12.8
8
40
0
80
10
51.2
25.6
9
40
0
90
10
102.4
51.2
…
…
…
…
…
…
…
30
40
0
300
10
214748364.8
107374182.4
我们来计算三种方案所得回报的增长情况:
从表格中获取信息,体会三种函数的增长差异。
图-1
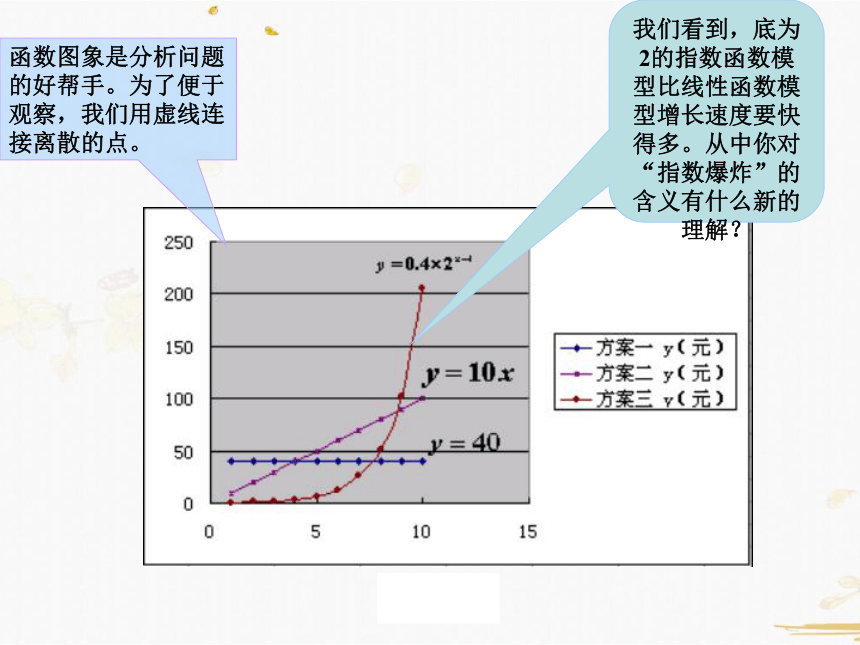
我们看到,底为2的指数函数模型比线性函数模型增长速度要快得多。从中你对“指数爆炸”的含义有什么新的理解?
函数图象是分析问题的好帮手。为了便于观察,我们用虚线连接离散的点。
图112-1
从每天的回报量来看: 第1~4天,方案一最多; 每5~8天,方案二最多; 第9天以后,方案三最多.
有人认为投资1~4天选择方案一;5~8天选择方案二;9天以后选择方案三?
下面再看累计的回报数:
结论:投资1~6天,应选择方案一;投资7天,应选择方案一或方案二;投资8 ~ 10天,应选择方案二;投资11天(含11天)以上,应选择方案三。
天数
回报/元
方案
一
二
三
40
1 2 3 4 5 6 7 8 9 10 11
80 120 160 200 240 280 320 360 400 440
10 30 60 100 150 210 280 360 450 550 660
0.4 1.2 2.8 6 12.4 25.2 50.8 102 204.4 409.2 818.8
解决实际问题的步骤:
实际问题
读懂问题
抽象概括
数学问题
演算
推理
数学问题的解
还原说明
实际问题的解
例2:在同一坐标系中y=log2x,y=2x,y=x?这三个函数图象的相对位置关系如何?请画出其大致图象.
x
y
o
1
1
2
4
y=2x
y=x2
y=log2x
y=log2x
结论.三个函数增长情况比较:
在区间(0, ,+∞)上,尽管函数y=logax(a>1),y=ax(a>1)与y=xn(n>0)都是增函数,但它们的增长速度不同,而且不在同一个“档次”上。随着x的增大,y=ax(a>1)的增长速度越来越快,会超过并远远大于y=xn(n>0)的增长速度,而y=logax(a>1)的增长速度则会越来越慢. 因此总存在一个x0,当x> x0时,就会有 logaxx
y
o
1
1
2
4
y=2x
y=x2
y=log2x
y=log2x
90
80
70
60
50
40
30
20
10
v
t
1
2
3
4
5
例3:一辆汽车在某段路程的行驶速度与时间关系如图所示:(1)求图中阴影部分的面积,并说明所求面积的实际含义;(2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004 km,试建立汽车行驶这段路程时汽车里程表读数s km与时间t h的函数解析式,并作出相应的图象
2000
2100
2200
2300
2400
0
1
2
3
4
5
t
s
(2)解:
1. 读题,找关键点;
2. 抽象成数学模型;
3. 求出数学模型的解;
4. 做答.
解题方法:
归 纳
例5:某桶装水销售部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元,销售单价与日均销售量的关系如表所示:
请根据以上数据作出分析,这个经营部怎样定价才能获得最大利润?
销售单价(元)
6
7
8
9
10
11
12
日均销量(桶)
480
440
400
360
320
280
240
解:设每桶水定价为x元时,日销售利润为y元,
则日均销售量为 桶
而
有最大值
只需将销售单价定为11.5元,就可获得最大的利润
解应用题的策略
一般思路可表示如下:
实际问题
数学问题
实际问题结论
数学问题结论
问题解决
数学解答
(转化为数学问题)
数学化
(回到实际问题)
符合实际
还原说明
抽象概括
推
理
演
算
课堂小结
本节我们通过分析一些实际问题背景,尝试运用所学函数模型去解决问题,初步认识并体会了函数应用的基本方法和步骤。我们要在逐步应用的过程中掌握这一问题的解题策略。常见的函数模型有:一次函数、二次函数、分段函数及简单的指对函数。
函数是描述客观世界变化规律的基本数学模型,不同的变化规律需要不同的函数模型来描述的,我们学过的函数模型有哪些呢?
一次函数 二次函数 指数函数 对数函数 幂函数 等等
对于实际问题,我们如何选择一个恰当的函数模型来刻画它呢?找出模型后又是如何去研究它的性质呢?
例1 、 假设你有一笔资金用于投资,现在有三种投资方案供你选择,这三种方案的回报如下:
方案一、每天回报40元;
方案二、第一天回报10元,以后每天比前一天多回报10元;
方案三、第一天回报0.4元,以后每天的回报比前一天翻一番。
请问,你会选择哪种投资方案?
我们可以先建立三种投资方案所对应的函数模型,再通过比较它们的增长情况,为选择投资方案提供依据。
解:设第x天所得回报为y元,则
方案一:每天回报40元; y=40 (x∈N*)
方案二:第一天回报10元,以后每天比前一天多回 报10元; y=10x (x∈N*)
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番。
y=0.4×2x-1 (x∈N*)
投资方案选择原则:
投入资金相同,回报量多者为优
(1)比较三种方案每天回报量
(2)比较三种方案一段时间内的总回报量
哪个方案在某段时间内的总回报量最多,我们就在那段时间选择该方案。
(3)三个函数模型的增减性如何?
(4)要对三个方案作出选择,就要对它们的增长情况进行分析,如何分析?
x/天
方案一
方案二
方案三
y/元
增长量/元
y/元
增长量/元
y/元
增长量/元
1
40
10
0.4
2
40
0
20
10
0.8
0.4
3
40
0
30
10
1.6
0.8
4
40
0
40
10
3.2
1.6
5
40
0
50
10
6.4
3.2
6
40
0
60
10
12.8
6.4
7
40
0
70
10
25.6
12.8
8
40
0
80
10
51.2
25.6
9
40
0
90
10
102.4
51.2
…
…
…
…
…
…
…
30
40
0
300
10
214748364.8
107374182.4
我们来计算三种方案所得回报的增长情况:
从表格中获取信息,体会三种函数的增长差异。
图-1
我们看到,底为2的指数函数模型比线性函数模型增长速度要快得多。从中你对“指数爆炸”的含义有什么新的理解?
函数图象是分析问题的好帮手。为了便于观察,我们用虚线连接离散的点。
图112-1
从每天的回报量来看: 第1~4天,方案一最多; 每5~8天,方案二最多; 第9天以后,方案三最多.
有人认为投资1~4天选择方案一;5~8天选择方案二;9天以后选择方案三?
下面再看累计的回报数:
结论:投资1~6天,应选择方案一;投资7天,应选择方案一或方案二;投资8 ~ 10天,应选择方案二;投资11天(含11天)以上,应选择方案三。
天数
回报/元
方案
一
二
三
40
1 2 3 4 5 6 7 8 9 10 11
80 120 160 200 240 280 320 360 400 440
10 30 60 100 150 210 280 360 450 550 660
0.4 1.2 2.8 6 12.4 25.2 50.8 102 204.4 409.2 818.8
解决实际问题的步骤:
实际问题
读懂问题
抽象概括
数学问题
演算
推理
数学问题的解
还原说明
实际问题的解
例2:在同一坐标系中y=log2x,y=2x,y=x?这三个函数图象的相对位置关系如何?请画出其大致图象.
x
y
o
1
1
2
4
y=2x
y=x2
y=log2x
y=log2x
结论.三个函数增长情况比较:
在区间(0, ,+∞)上,尽管函数y=logax(a>1),y=ax(a>1)与y=xn(n>0)都是增函数,但它们的增长速度不同,而且不在同一个“档次”上。随着x的增大,y=ax(a>1)的增长速度越来越快,会超过并远远大于y=xn(n>0)的增长速度,而y=logax(a>1)的增长速度则会越来越慢. 因此总存在一个x0,当x> x0时,就会有 logax
y
o
1
1
2
4
y=2x
y=x2
y=log2x
y=log2x
90
80
70
60
50
40
30
20
10
v
t
1
2
3
4
5
例3:一辆汽车在某段路程的行驶速度与时间关系如图所示:(1)求图中阴影部分的面积,并说明所求面积的实际含义;(2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004 km,试建立汽车行驶这段路程时汽车里程表读数s km与时间t h的函数解析式,并作出相应的图象
2000
2100
2200
2300
2400
0
1
2
3
4
5
t
s
(2)解:
1. 读题,找关键点;
2. 抽象成数学模型;
3. 求出数学模型的解;
4. 做答.
解题方法:
归 纳
例5:某桶装水销售部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元,销售单价与日均销售量的关系如表所示:
请根据以上数据作出分析,这个经营部怎样定价才能获得最大利润?
销售单价(元)
6
7
8
9
10
11
12
日均销量(桶)
480
440
400
360
320
280
240
解:设每桶水定价为x元时,日销售利润为y元,
则日均销售量为 桶
而
有最大值
只需将销售单价定为11.5元,就可获得最大的利润
解应用题的策略
一般思路可表示如下:
实际问题
数学问题
实际问题结论
数学问题结论
问题解决
数学解答
(转化为数学问题)
数学化
(回到实际问题)
符合实际
还原说明
抽象概括
推
理
演
算
课堂小结
本节我们通过分析一些实际问题背景,尝试运用所学函数模型去解决问题,初步认识并体会了函数应用的基本方法和步骤。我们要在逐步应用的过程中掌握这一问题的解题策略。常见的函数模型有:一次函数、二次函数、分段函数及简单的指对函数。
