高中数学人教A必修一课件-1.1.2集合间的基本关系(17张ppt)
文档属性
| 名称 | 高中数学人教A必修一课件-1.1.2集合间的基本关系(17张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 431.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-13 12:51:15 | ||
图片预览





文档简介
复习
1.集合、元素的概念
2.集合的分类:有限集、无限集、空集
3.集合元素的特性:确定性、互异性,无序性
4.集合的主要表示方法:列举法、描述法
5.常用数集:
补充几点:
课本第5页练习2(3):
试选择适当的方法表示下列集合:一次函数y=x+3与y=-2x+6的图像的交点组成的集合。
解:可采用列举法表示。先求出一次函数y=x+3与y=-2x+6的图像的交点。因 y=x+3 的解
y=-2x+6
为x=1,y=4 。所以用列举法表示该集合为:
{(1,4)}。
思考:能不能用描述法表示该集合呢?
1.1.2
集合间的基本关系
观察以下几组集合,并指出它们元
素间的关系:
① A={1,2,3}, B={1,2,3,4,5};
② A={x| x是江苏人}, B={x | x是中国人};
③ A={x | x是两边相等的三角形},
B={x| x是等腰三角形} .
子集的定义
一般地,对于两个集合A与B, 如果集合A中的任何一个元素都是 集合B的元素,我们就说这两个集合有包含关系,称集合A为集合B的子集(subset)
记作 A B(或B A)
读作“A含于B”,或“B包含A”.
B
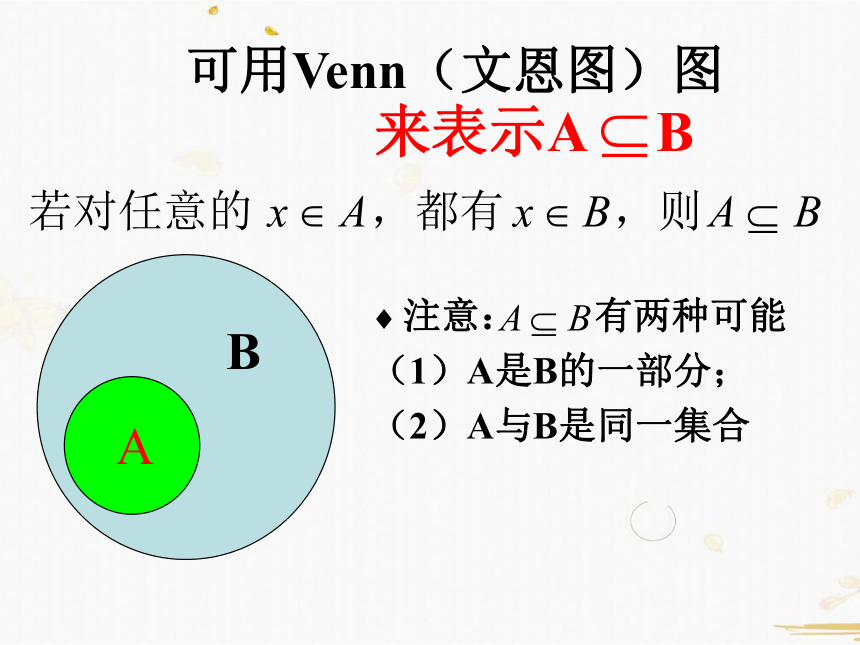
来表示A B
A
可用Venn(文恩图)图
注意: 有两种可能
(1)A是B的一部分;
(2)A与B是同一集合
B
A
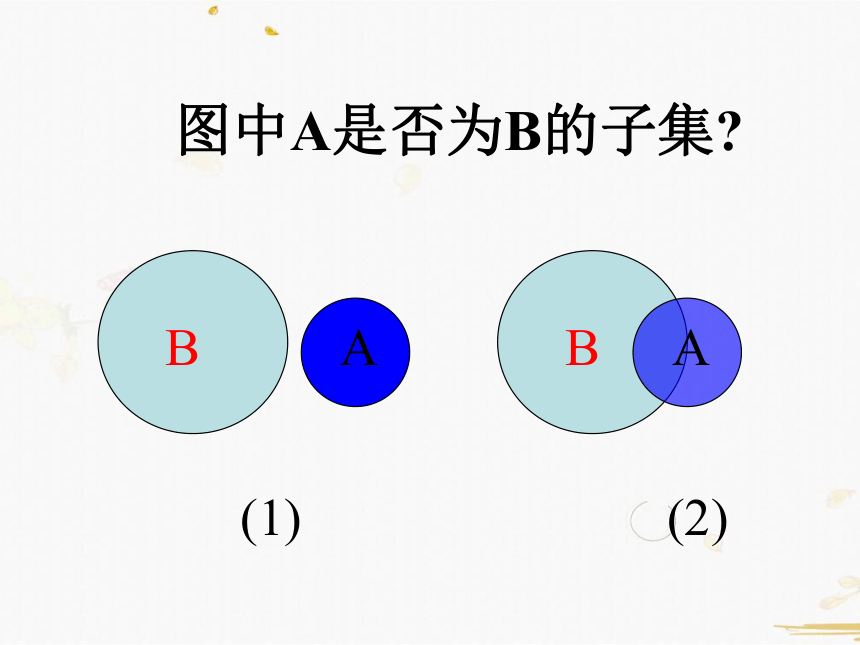
图中A是否为B的子集?
(1)
B
A
(2)
判断集合A是否为集合B的子集,若是则在( )打√,若不是则在( )打×:
①A={1,3,5}, B={1,2,3,4,5,6} ( )
②A={1,3,5}, B={1,3,6,9} ( )
③A={0}, B={x x2+2=0} ( )
④A={a,b,c,d}, B={d,b,c,a} ( )
×
×
√
√
一般地,对于两个集合A与B, 如果集合A中的任何一个元素都是 集合B的元素,同时集合B中的任何一个元素都是集合A的元素,则称集合A等于集合B,记作
A=B
集合相等的定义
若A B且B A,
则A=B;
反之,亦然.
真子集的定义
Venn图为
A
B
对于两个集合A与B,如果A B,但存在元素 ,则称集合A是集合B的真子集(proper subset).记作A B
空集的定义
我们把不含任何元素的集合叫做空集,记为Φ或 { }。并规定空集是任何集合的子集。
例如,A={x|x2+2=0}= Φ
注意的是{φ}不是空集,而是一个单元素集合,它的元素是“φ”。
几个结论
①空集是任何集合的子集 Φ A
②空集是任何非空集合的真子集
Φ A (A ≠ Φ)
③任何一个集合是它本身的子集,即 A A
④对于集合A,B,C,如果 A B,
且B C,则A C
重要结论
含有n个元素的集合,它的所有子集个数是2n个;所有真子集的个数是2n-1个;所有非空真子集数为2n-2个。
课堂练习
课本第7页1—3题。
扩展练习
1、已知A={a-2,2a?+5a,10},且
-3∈A,求a。
2、设A={x,x2,xy}, B={1,x,y},且A=B, 求实数x,y的值.
3、已知
课堂小结
1.子集,真子集的概念与性质;
3.空集的概念及性质
2. 集合相等的概念;
作业布置
1、教材P.7第1题
2、教材P.12 A组 第5 题
1.集合、元素的概念
2.集合的分类:有限集、无限集、空集
3.集合元素的特性:确定性、互异性,无序性
4.集合的主要表示方法:列举法、描述法
5.常用数集:
补充几点:
课本第5页练习2(3):
试选择适当的方法表示下列集合:一次函数y=x+3与y=-2x+6的图像的交点组成的集合。
解:可采用列举法表示。先求出一次函数y=x+3与y=-2x+6的图像的交点。因 y=x+3 的解
y=-2x+6
为x=1,y=4 。所以用列举法表示该集合为:
{(1,4)}。
思考:能不能用描述法表示该集合呢?
1.1.2
集合间的基本关系
观察以下几组集合,并指出它们元
素间的关系:
① A={1,2,3}, B={1,2,3,4,5};
② A={x| x是江苏人}, B={x | x是中国人};
③ A={x | x是两边相等的三角形},
B={x| x是等腰三角形} .
子集的定义
一般地,对于两个集合A与B, 如果集合A中的任何一个元素都是 集合B的元素,我们就说这两个集合有包含关系,称集合A为集合B的子集(subset)
记作 A B(或B A)
读作“A含于B”,或“B包含A”.
B
来表示A B
A
可用Venn(文恩图)图
注意: 有两种可能
(1)A是B的一部分;
(2)A与B是同一集合
B
A
图中A是否为B的子集?
(1)
B
A
(2)
判断集合A是否为集合B的子集,若是则在( )打√,若不是则在( )打×:
①A={1,3,5}, B={1,2,3,4,5,6} ( )
②A={1,3,5}, B={1,3,6,9} ( )
③A={0}, B={x x2+2=0} ( )
④A={a,b,c,d}, B={d,b,c,a} ( )
×
×
√
√
一般地,对于两个集合A与B, 如果集合A中的任何一个元素都是 集合B的元素,同时集合B中的任何一个元素都是集合A的元素,则称集合A等于集合B,记作
A=B
集合相等的定义
若A B且B A,
则A=B;
反之,亦然.
真子集的定义
Venn图为
A
B
对于两个集合A与B,如果A B,但存在元素 ,则称集合A是集合B的真子集(proper subset).记作A B
空集的定义
我们把不含任何元素的集合叫做空集,记为Φ或 { }。并规定空集是任何集合的子集。
例如,A={x|x2+2=0}= Φ
注意的是{φ}不是空集,而是一个单元素集合,它的元素是“φ”。
几个结论
①空集是任何集合的子集 Φ A
②空集是任何非空集合的真子集
Φ A (A ≠ Φ)
③任何一个集合是它本身的子集,即 A A
④对于集合A,B,C,如果 A B,
且B C,则A C
重要结论
含有n个元素的集合,它的所有子集个数是2n个;所有真子集的个数是2n-1个;所有非空真子集数为2n-2个。
课堂练习
课本第7页1—3题。
扩展练习
1、已知A={a-2,2a?+5a,10},且
-3∈A,求a。
2、设A={x,x2,xy}, B={1,x,y},且A=B, 求实数x,y的值.
3、已知
课堂小结
1.子集,真子集的概念与性质;
3.空集的概念及性质
2. 集合相等的概念;
作业布置
1、教材P.7第1题
2、教材P.12 A组 第5 题
