27.2 与圆有关的位置关系 同步练习(含解析)
文档属性
| 名称 | 27.2 与圆有关的位置关系 同步练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-12 15:53:15 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
初中数学华师大版九年级下学期 第27章 27.2 与圆有关的位置关系
一、单选题
1.已知⊙O的半径为4cm.若点P到圆心O的距离为3cm,则点P( )
A.?在⊙O内???????????????????B.?在⊙O上???????????????????C.?在⊙O外???????????????????D.?与⊙O的位置关系无法确定
2.如图,四边形 中, .若 .则 外心与 外心的距离是(? )
A.?5??????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
3.已知 的半径是 ,圆心 到同一平面内直线 的距离为 ,则直线 与 的位置关系是(?? ) 21世纪教育网版权所有
A.?相交??????????????????????????????????B.?相切??????????????????????????????????C.?相离??????????????????????????????????D.?无法判断
4.如图,以点P为圆心作圆,所得的圆与直线l相切的是(??? )
A.?以PA为半径的圆????????????B.?以PB为半径的圆????????????C.?以PC为半径的圆????????????D.?以PD为半径的圆
5.如图所示,∠APB=30°,O为PA上一点,且PO=6,以点O为圆心,半径为3 的圆与PB的位置关系是(?? ) 21·cn·jy·com
A.?相离??????????????????????????????B.?相切??????????????????????????????C.?相交??????????????????????????????D.?相切、相离或相交
6.已知⊙O的半径r=3,设圆心O到一条直线的距离为d,圆上到这条直线的距离为2的点的个数为m,给出下列命题:www-2-1-cnjy-com
①若d>5,则m=0;②若d=5,则m=1;③若1<d<5,则m=3;④若d=1,则m=2;⑤若d<1,则m=4.
其中正确命题的个数是(??? )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?5
7.如图,P为圆O外一点, 分别切圆O于 两点,若 ,则 (?? ).
A.?2???????????????????????????????????????????B.?3???????????????????????????????????????????C.?4???????????????????????????????????????????D.?5
8.如图, 、 、 与圆O相切, ,则 (??? )
A.?50°???????????????????????????????????????B.?60°???????????????????????????????????????C.?70°???????????????????????????????????????D.?80°
二、填空题
9.若圆 的半径是 ,圆心的坐标是 ,点 的坐标是 ,则点 与 的位置关系是________(选填“在圆上”、“在圆外”或“在圆内”) 2-1-c-n-j-y
10.如图, 、 、 分别切 于点 、 、 , 交 、 于点 、 ,已知 长 ,则 的周长为________. 21*cnjy*com
11.如图, , 是 的切线, , 为切点, 是 的直径, ,则 的度数为________. 【来源:21cnj*y.co*m】
三、解答题
12.如图,已知△ABC,请用尺规作△ABC的外接圆⊙O.(保留作图痕迹,不写作法)
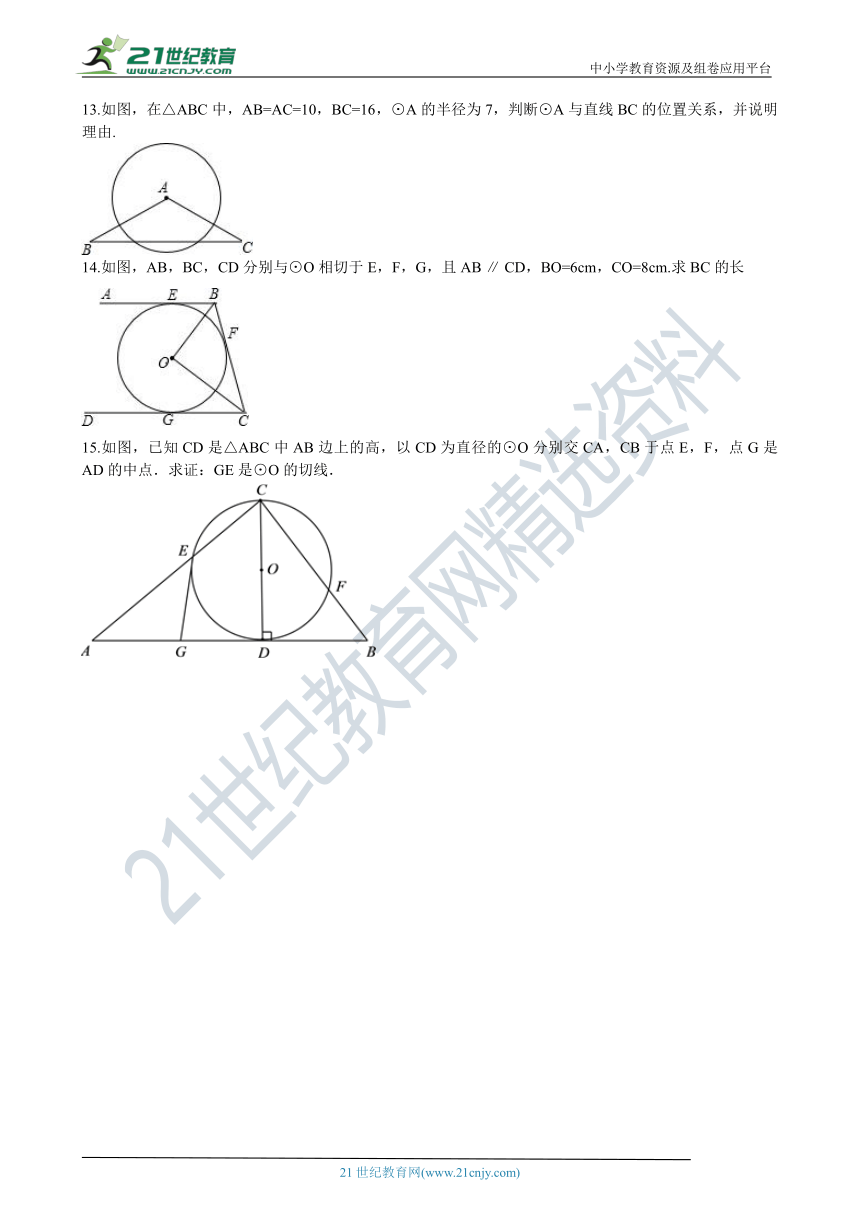
13.如图,在△ABC中,AB=AC=10,BC=16,⊙A的半径为7,判断⊙A与直线BC的位置关系,并说明理由. 【出处:21教育名师】
14.如图,AB,BC,CD分别与⊙O相切于E,F,G,且AB ∥ CD,BO=6cm,CO=8cm.求BC的长
15.如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O分别交CA,CB于点E,F,点G是AD的中点.求证:GE是⊙O的切线. 【版权所有:21教育】
答案解析部分
一、单选题
1.【答案】 A
解:∵_d=3,r=_4,
∴d ∴点P在⊙O内;
故答案为:A.
2.【答案】 A
解:如图,连接AC,作 于F,AC与BD、DF交于点E、G,
垂直平分BD,
,
是等边三角形, 是等腰直角三角形
是 的外心, 是 的外心,
在 中,
在 中,
?
故 外心与 外心的距离是5
故答案为:A.
3.【答案】 A
解:根据题意可知:4>3,
∴直线与圆相交;
故答案为:A.
4.【答案】 B
解:∵PB⊥l于B,
∴以点P为圆心,PB为半径的圆与直线l相切.
故答案为:B.
5.【答案】 C
解:过O作OC⊥PB于C,
∵∠APB=30°,OP=6,
∴OC= OP=3<3 ,
∴半径为3 的圆与PB的位置关系是相交,
故答案为:C.
6.【答案】 C
解:①若d>5时,∵d﹥r,∴直线与圆相离,又∵d-r﹥2,则m=0,故正确;
②若d=5时,∵d﹥r,∴直线与圆相离,又∵d-r=2,则m=1,故正确;
③若1<d<5,则m=2,故错误;
④若d=1时,直线与圆相交,则m=3,故错误;
⑤若d<1时,直线与圆相交,则m=4,故正确.
故答案为:C.
7.【答案】 D
解:∵P为圆O外一点,PA,PB分别切圆O于A,B两点,若PA=5,
∴PB=PA=5,
故答案为:D.
8.【答案】 B
解:设PA、PB、AB分别与⊙O相切于点C、D、E,然后连接OC、OD、OE,如图所示: 21·世纪*教育网
∵ 、 、 与圆O相切,
∴∠OCA=∠ODB=∠OEB=90°,OC=OD=OE,
∴OA、OB分别平分∠EOC、∠EOD,
∵∠P=60°,
∴∠COD=120°,
∴ ,
∴ ,
故答案为:B.
二、填空题
9.【答案】 在圆上
解:∵点P的坐标是(?4,3),
∴OP= =5,
∵OP等于圆O的半径,
∴点P在圆O上.
故填:点P在圆O上.
10.【答案】 cm
解:∵PA、PB、DE分别切⊙O于A、B、C,
∴PA=PB,DA=DC,EC=EB;
∴C△PDE=PD+DE+PE=PD+DA+EB+PE=PA+PB=8+8=16cm;
∴△PDE的周长为16cm.
故答案为16cm.
11.【答案】 70°
解:连接OB:
∵PA、PB是⊙O的两条切线,A、B是切点,AC是⊙O的直径,
∴∠OAP=∠OBP=90°,
∵∠BAC=35°,OA=OB,
∴∠BAC=∠OBA=35°,
∴∠PAB=∠PBA=55°,
∴∠P=180°?∠PAB?∠PBA=70°,
即∠P的度数是70°,
故答案为:70°.
三、解答题
12.【答案】 解:如图,⊙O即为所求作.
13.【答案】 解:⊙A与直线BC相交.
过A作AD⊥BC,垂足为点D.
∵AB=AC,BC=16,
∴BD= BC= ×16=8,
在Rt△ABC中,AB=10,BD=8,
∴AD= =6,
∵⊙O的半径为7,
∴AD<r,
⊙A与直线BC相交.
14.【答案】 解:∵AB,BC,CD分别与⊙O相切于E,F,G;
∴∠CBO= ∠ABC,∠BCO= ∠DCB,
∵AB∥CD,
∴∠ABC+∠DCB=180°,
∴∠CBO+∠BCO= ∠ABC+∠DCB= (∠ABC+∠DCB)=90°.
∴BC= cm.
15.【答案】 解:连接OE,DE,
∵CD是⊙O的直径,
∴∠AED=∠CED=90°,
∵G是AD的中点,
∴EG= AD=DG,
∴∠1=∠2;
∵OE=OD,
∴∠3=∠4,
∴∠1+∠3=∠2+∠4,
∴∠OEG=∠ODG=90°,
故GE是⊙O的切线.
_21?????????è?????(www.21cnjy.com)_
初中数学华师大版九年级下学期 第27章 27.2 与圆有关的位置关系
一、单选题
1.已知⊙O的半径为4cm.若点P到圆心O的距离为3cm,则点P( )
A.?在⊙O内???????????????????B.?在⊙O上???????????????????C.?在⊙O外???????????????????D.?与⊙O的位置关系无法确定
2.如图,四边形 中, .若 .则 外心与 外心的距离是(? )
A.?5??????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
3.已知 的半径是 ,圆心 到同一平面内直线 的距离为 ,则直线 与 的位置关系是(?? ) 21世纪教育网版权所有
A.?相交??????????????????????????????????B.?相切??????????????????????????????????C.?相离??????????????????????????????????D.?无法判断
4.如图,以点P为圆心作圆,所得的圆与直线l相切的是(??? )
A.?以PA为半径的圆????????????B.?以PB为半径的圆????????????C.?以PC为半径的圆????????????D.?以PD为半径的圆
5.如图所示,∠APB=30°,O为PA上一点,且PO=6,以点O为圆心,半径为3 的圆与PB的位置关系是(?? ) 21·cn·jy·com
A.?相离??????????????????????????????B.?相切??????????????????????????????C.?相交??????????????????????????????D.?相切、相离或相交
6.已知⊙O的半径r=3,设圆心O到一条直线的距离为d,圆上到这条直线的距离为2的点的个数为m,给出下列命题:www-2-1-cnjy-com
①若d>5,则m=0;②若d=5,则m=1;③若1<d<5,则m=3;④若d=1,则m=2;⑤若d<1,则m=4.
其中正确命题的个数是(??? )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?5
7.如图,P为圆O外一点, 分别切圆O于 两点,若 ,则 (?? ).
A.?2???????????????????????????????????????????B.?3???????????????????????????????????????????C.?4???????????????????????????????????????????D.?5
8.如图, 、 、 与圆O相切, ,则 (??? )
A.?50°???????????????????????????????????????B.?60°???????????????????????????????????????C.?70°???????????????????????????????????????D.?80°
二、填空题
9.若圆 的半径是 ,圆心的坐标是 ,点 的坐标是 ,则点 与 的位置关系是________(选填“在圆上”、“在圆外”或“在圆内”) 2-1-c-n-j-y
10.如图, 、 、 分别切 于点 、 、 , 交 、 于点 、 ,已知 长 ,则 的周长为________. 21*cnjy*com
11.如图, , 是 的切线, , 为切点, 是 的直径, ,则 的度数为________. 【来源:21cnj*y.co*m】
三、解答题
12.如图,已知△ABC,请用尺规作△ABC的外接圆⊙O.(保留作图痕迹,不写作法)
13.如图,在△ABC中,AB=AC=10,BC=16,⊙A的半径为7,判断⊙A与直线BC的位置关系,并说明理由. 【出处:21教育名师】
14.如图,AB,BC,CD分别与⊙O相切于E,F,G,且AB ∥ CD,BO=6cm,CO=8cm.求BC的长
15.如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O分别交CA,CB于点E,F,点G是AD的中点.求证:GE是⊙O的切线. 【版权所有:21教育】
答案解析部分
一、单选题
1.【答案】 A
解:∵_d=3,r=_4,
∴d
故答案为:A.
2.【答案】 A
解:如图,连接AC,作 于F,AC与BD、DF交于点E、G,
垂直平分BD,
,
是等边三角形, 是等腰直角三角形
是 的外心, 是 的外心,
在 中,
在 中,
?
故 外心与 外心的距离是5
故答案为:A.
3.【答案】 A
解:根据题意可知:4>3,
∴直线与圆相交;
故答案为:A.
4.【答案】 B
解:∵PB⊥l于B,
∴以点P为圆心,PB为半径的圆与直线l相切.
故答案为:B.
5.【答案】 C
解:过O作OC⊥PB于C,
∵∠APB=30°,OP=6,
∴OC= OP=3<3 ,
∴半径为3 的圆与PB的位置关系是相交,
故答案为:C.
6.【答案】 C
解:①若d>5时,∵d﹥r,∴直线与圆相离,又∵d-r﹥2,则m=0,故正确;
②若d=5时,∵d﹥r,∴直线与圆相离,又∵d-r=2,则m=1,故正确;
③若1<d<5,则m=2,故错误;
④若d=1时,直线与圆相交,则m=3,故错误;
⑤若d<1时,直线与圆相交,则m=4,故正确.
故答案为:C.
7.【答案】 D
解:∵P为圆O外一点,PA,PB分别切圆O于A,B两点,若PA=5,
∴PB=PA=5,
故答案为:D.
8.【答案】 B
解:设PA、PB、AB分别与⊙O相切于点C、D、E,然后连接OC、OD、OE,如图所示: 21·世纪*教育网
∵ 、 、 与圆O相切,
∴∠OCA=∠ODB=∠OEB=90°,OC=OD=OE,
∴OA、OB分别平分∠EOC、∠EOD,
∵∠P=60°,
∴∠COD=120°,
∴ ,
∴ ,
故答案为:B.
二、填空题
9.【答案】 在圆上
解:∵点P的坐标是(?4,3),
∴OP= =5,
∵OP等于圆O的半径,
∴点P在圆O上.
故填:点P在圆O上.
10.【答案】 cm
解:∵PA、PB、DE分别切⊙O于A、B、C,
∴PA=PB,DA=DC,EC=EB;
∴C△PDE=PD+DE+PE=PD+DA+EB+PE=PA+PB=8+8=16cm;
∴△PDE的周长为16cm.
故答案为16cm.
11.【答案】 70°
解:连接OB:
∵PA、PB是⊙O的两条切线,A、B是切点,AC是⊙O的直径,
∴∠OAP=∠OBP=90°,
∵∠BAC=35°,OA=OB,
∴∠BAC=∠OBA=35°,
∴∠PAB=∠PBA=55°,
∴∠P=180°?∠PAB?∠PBA=70°,
即∠P的度数是70°,
故答案为:70°.
三、解答题
12.【答案】 解:如图,⊙O即为所求作.
13.【答案】 解:⊙A与直线BC相交.
过A作AD⊥BC,垂足为点D.
∵AB=AC,BC=16,
∴BD= BC= ×16=8,
在Rt△ABC中,AB=10,BD=8,
∴AD= =6,
∵⊙O的半径为7,
∴AD<r,
⊙A与直线BC相交.
14.【答案】 解:∵AB,BC,CD分别与⊙O相切于E,F,G;
∴∠CBO= ∠ABC,∠BCO= ∠DCB,
∵AB∥CD,
∴∠ABC+∠DCB=180°,
∴∠CBO+∠BCO= ∠ABC+∠DCB= (∠ABC+∠DCB)=90°.
∴BC= cm.
15.【答案】 解:连接OE,DE,
∵CD是⊙O的直径,
∴∠AED=∠CED=90°,
∵G是AD的中点,
∴EG= AD=DG,
∴∠1=∠2;
∵OE=OD,
∴∠3=∠4,
∴∠1+∠3=∠2+∠4,
∴∠OEG=∠ODG=90°,
故GE是⊙O的切线.
_21?????????è?????(www.21cnjy.com)_
