27.4 正多边形和圆 同步练习(含解析)
文档属性
| 名称 | 27.4 正多边形和圆 同步练习(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-12 16:00:29 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
初中数学华师大版九年级下学期 第27章 27.4 正多边形和圆
一、单选题
1.正方形外接圆的半径为4,则其内切圆的半径为(?? )
A.?2 ???????????????????????????????????????B.????????????????????????????????????????C.?1???????????????????????????????????????D.?
2.半径为 的圆内接正三角形的面积是( ?)
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
3.将每一个内角都是108°的五边形按如图所示方式放置,若直线m∥n , 则下列结论中一定正确的是(? ???)
A.?∠1=∠2+36°???????????????????B.?∠1=∠2+72°???????????????????C.?∠1+∠2=90°???????????????????D.?2∠1+∠2=180°
4.如图,半径为1的⊙O与正五边形ABCDE相切于点A、C,则劣弧AC的长度为(?? )
A.?π?????????????????????????????????????B.?π?????????????????????????????????????C.?π?????????????????????????????????????D.?π
5.如图,将边长_???3?????????è??_形铁丝框ABCDEF(面积记为S1)变形为以点D为圆心,CD为半径的扇形(面积记为S2),则S1与S2的关系为(?? ) 2·1·c·n·j·y
A.?S1>S2?????????????????????????????B.?S1=S2?????????????????????????????C.?S1<S2?????????????????????????????D.?S1= S2
6.如图中有两张型号完全_?????·????????????_饭桌,将正方形桌面边上的四个弓形翻折起来后,就能形成一个圆形桌面(可以近似看作正方形的外接圆),正方形桌面与翻折成圆形桌面的面积之比最接近(? )
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
二、填空题
7.一个半径为4cm的圆内接正六边形的面积等于________cm2 .
8.如图,正六边形ABCDEF内接于 ,若 ,则 的半径为________.
9.如图,正六边形ABCDEF内接于 ,半径为4,则这个正六边形的边心距OM的长为________.
10.如图, 是正方形ABCD的内切圆,切点分别为E、F,G,H,ED与 相交于点M,则sin∠MFG的值为________. www.21-cn-jy.com
三、解答题
11.如图,已知圆O内接正六边形 的边长为 ,求这个正六边形的边心距n , 面积S .
12.正六边形的边长为8,则阴影部分的面积是多少?
答案解析部分
一、单选题
1.【答案】 A
解:如图所示,连接OA、OE,
∵AB是小圆的切线,
∴OE⊥AB,
∵四边形ABCD是正方形,
∴∠OAE=45°,
∴△AOE是等腰直角三角形,AE=OE,
∴OE= OA= ×4=2 ,
故答案为:A.
2.【答案】 D
解:如图所示,过O作OD⊥BC于D;
∵此三角形是正三角形,
∴∠BOC= =120°.
∵OB=OC,
∴∠BOD= ×120°=60°,
∴∠OBD=30°;
∵OB=R,
∴OD= ,BD=OB?cos30°= ,
∴BC=2BD=2× = ,
∴S△BOC= ×BC×OD= × = ,
∴S△ABC=3× .
故答案为:D.
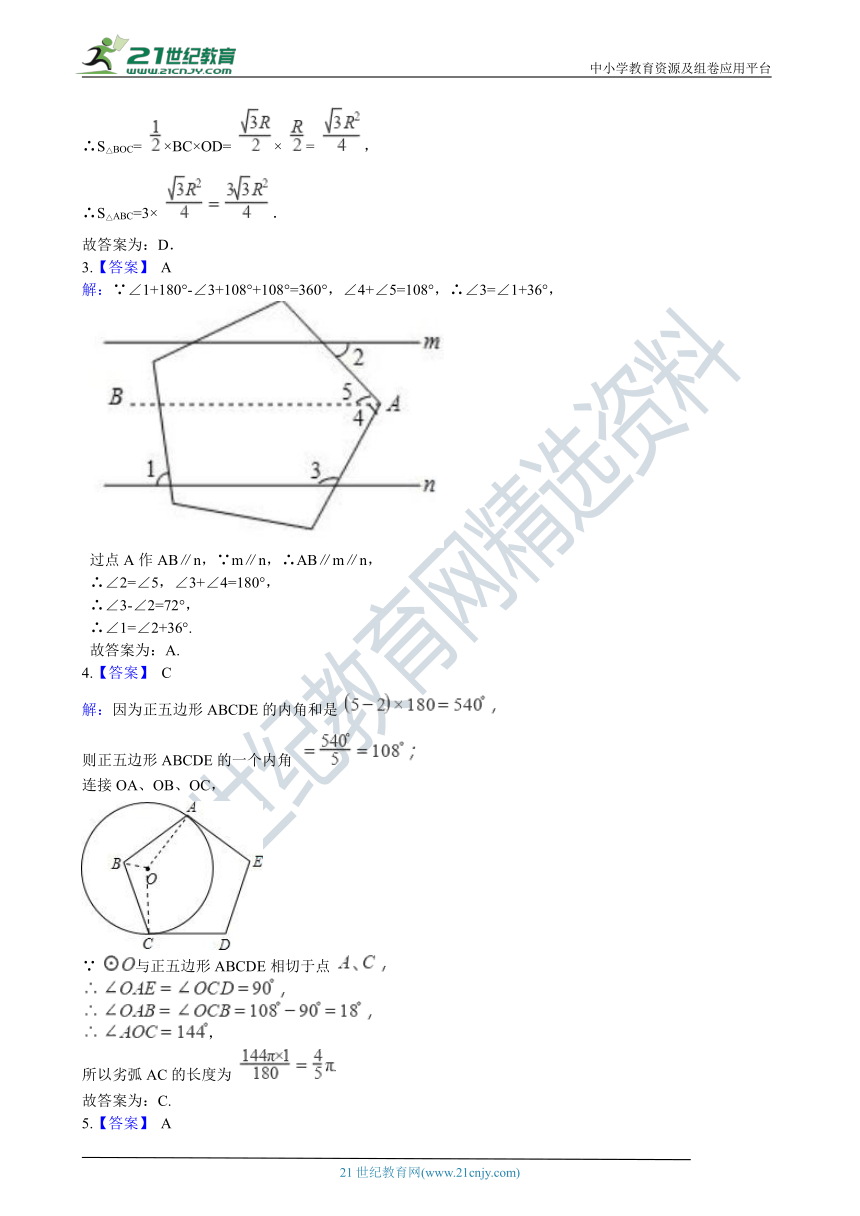
3.【答案】 A
解:∵∠1+180°-∠3+108°+108°=360°,∠4+∠5=108°,∴∠3=∠1+36°,
过点A作AB∥n,∵m∥n,∴AB∥m∥n,
∴∠2=∠5,∠3+∠4=180°,
∴∠3-∠2=72°,
∴∠1=∠2+36°.
故答案为:A.
4.【答案】 C
解:因为正五边形ABCDE的内角和是
则正五边形ABCDE的一个内角
连接OA、OB、OC,
∵ 与正五边形ABCDE相切于点
,
所以劣弧AC的长度为
故答案为:C.
5.【答案】 A
解:由题意: =12,
∴S2= ×12×3=18,
∵S1=6× ×32= ,
∴S1>S2 ,
故答案为:A.
6.【答案】 C
解:连接AC,
设正方形的边长为a,
∵四边形ABCD是正方形,
∴∠B=90°,
∴AC为圆的直径,
∴AC= AB= a,
则正方形桌面与翻折成的圆形桌面的面积之比为: ,
故答案为:C.
二、填空题
7.【答案】
解:一个圆的内接正六边形可以分成6个全等的等边三角形,
∵圆的半径是4cm,
∴等边三角形的边长是4cm,
如图,
边长是4cm的等边三角形,
根据等边三角形的性质, , ,
根据勾股定理, ,
,
∴内接正六边形的面积是 .
故答案是: .
8.【答案】 3cm
解:连接OA,OB,
∵ 正六边形ABCDEF内接于?,
∴∠AOB=60°,
∴△AOB为等边三角形,
∴AO=AB=3cm.
故答案为:3cm.
9.【答案】
解:如图,连结OC、OB,
∵正六边形ABCDEF内接于 ,
∴∠BOC=60?,
∵OC=OB,
∴△BOC为等边三角形,
∴∠OBM=60?,
∴OM=OM?sin∠OBM=4× ,
故答案为: .
10.【答案】
解:如图,连接EG、HF
由正方形内切圆的性质得:EG与HF的交点即为圆心O
四边形ABCD是正方形
由圆的切线的性质得:
四边形ADGE和四边形OHDG均为矩形
,
设正方形ABCD的边长为 ,则
的半径为
在 中,
由圆周角定理得:
则
故答案为: .
三、解答题
11.【答案】 解:连接OA、OB,过点O作OH⊥AB于点H,即边心距n=OH,如图所示:
∴AH=HB,∠AOH=BOH,
∵六边形ABCDEF是正六边形,
∴∠AOB=60°,AB=BC=CD=DE=EF=AF=6cm,
∵OA=OB,
∴△AOB是等边三角形,
∴AH=3cm,∠AOH=30°,OA=AB=6cm,
∴ ,
∴ ,
∴ .
12.【答案】 解:如图,连接OA、OB、OC;
由题意知:∠BOA=∠COA= =60°,
∵OA=OB=OC,
∴△OAB、△OAC均为等边三角形,
∴∠BAO=∠CAO=60°,
= ;
=32 ,
∴阴影部分的面积=3× =64π﹣96 .
_21?????????è?????(www.21cnjy.com)_
初中数学华师大版九年级下学期 第27章 27.4 正多边形和圆
一、单选题
1.正方形外接圆的半径为4,则其内切圆的半径为(?? )
A.?2 ???????????????????????????????????????B.????????????????????????????????????????C.?1???????????????????????????????????????D.?
2.半径为 的圆内接正三角形的面积是( ?)
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
3.将每一个内角都是108°的五边形按如图所示方式放置,若直线m∥n , 则下列结论中一定正确的是(? ???)
A.?∠1=∠2+36°???????????????????B.?∠1=∠2+72°???????????????????C.?∠1+∠2=90°???????????????????D.?2∠1+∠2=180°
4.如图,半径为1的⊙O与正五边形ABCDE相切于点A、C,则劣弧AC的长度为(?? )
A.?π?????????????????????????????????????B.?π?????????????????????????????????????C.?π?????????????????????????????????????D.?π
5.如图,将边长_???3?????????è??_形铁丝框ABCDEF(面积记为S1)变形为以点D为圆心,CD为半径的扇形(面积记为S2),则S1与S2的关系为(?? ) 2·1·c·n·j·y
A.?S1>S2?????????????????????????????B.?S1=S2?????????????????????????????C.?S1<S2?????????????????????????????D.?S1= S2
6.如图中有两张型号完全_?????·????????????_饭桌,将正方形桌面边上的四个弓形翻折起来后,就能形成一个圆形桌面(可以近似看作正方形的外接圆),正方形桌面与翻折成圆形桌面的面积之比最接近(? )
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
二、填空题
7.一个半径为4cm的圆内接正六边形的面积等于________cm2 .
8.如图,正六边形ABCDEF内接于 ,若 ,则 的半径为________.
9.如图,正六边形ABCDEF内接于 ,半径为4,则这个正六边形的边心距OM的长为________.
10.如图, 是正方形ABCD的内切圆,切点分别为E、F,G,H,ED与 相交于点M,则sin∠MFG的值为________. www.21-cn-jy.com
三、解答题
11.如图,已知圆O内接正六边形 的边长为 ,求这个正六边形的边心距n , 面积S .
12.正六边形的边长为8,则阴影部分的面积是多少?
答案解析部分
一、单选题
1.【答案】 A
解:如图所示,连接OA、OE,
∵AB是小圆的切线,
∴OE⊥AB,
∵四边形ABCD是正方形,
∴∠OAE=45°,
∴△AOE是等腰直角三角形,AE=OE,
∴OE= OA= ×4=2 ,
故答案为:A.
2.【答案】 D
解:如图所示,过O作OD⊥BC于D;
∵此三角形是正三角形,
∴∠BOC= =120°.
∵OB=OC,
∴∠BOD= ×120°=60°,
∴∠OBD=30°;
∵OB=R,
∴OD= ,BD=OB?cos30°= ,
∴BC=2BD=2× = ,
∴S△BOC= ×BC×OD= × = ,
∴S△ABC=3× .
故答案为:D.
3.【答案】 A
解:∵∠1+180°-∠3+108°+108°=360°,∠4+∠5=108°,∴∠3=∠1+36°,
过点A作AB∥n,∵m∥n,∴AB∥m∥n,
∴∠2=∠5,∠3+∠4=180°,
∴∠3-∠2=72°,
∴∠1=∠2+36°.
故答案为:A.
4.【答案】 C
解:因为正五边形ABCDE的内角和是
则正五边形ABCDE的一个内角
连接OA、OB、OC,
∵ 与正五边形ABCDE相切于点
,
所以劣弧AC的长度为
故答案为:C.
5.【答案】 A
解:由题意: =12,
∴S2= ×12×3=18,
∵S1=6× ×32= ,
∴S1>S2 ,
故答案为:A.
6.【答案】 C
解:连接AC,
设正方形的边长为a,
∵四边形ABCD是正方形,
∴∠B=90°,
∴AC为圆的直径,
∴AC= AB= a,
则正方形桌面与翻折成的圆形桌面的面积之比为: ,
故答案为:C.
二、填空题
7.【答案】
解:一个圆的内接正六边形可以分成6个全等的等边三角形,
∵圆的半径是4cm,
∴等边三角形的边长是4cm,
如图,
边长是4cm的等边三角形,
根据等边三角形的性质, , ,
根据勾股定理, ,
,
∴内接正六边形的面积是 .
故答案是: .
8.【答案】 3cm
解:连接OA,OB,
∵ 正六边形ABCDEF内接于?,
∴∠AOB=60°,
∴△AOB为等边三角形,
∴AO=AB=3cm.
故答案为:3cm.
9.【答案】
解:如图,连结OC、OB,
∵正六边形ABCDEF内接于 ,
∴∠BOC=60?,
∵OC=OB,
∴△BOC为等边三角形,
∴∠OBM=60?,
∴OM=OM?sin∠OBM=4× ,
故答案为: .
10.【答案】
解:如图,连接EG、HF
由正方形内切圆的性质得:EG与HF的交点即为圆心O
四边形ABCD是正方形
由圆的切线的性质得:
四边形ADGE和四边形OHDG均为矩形
,
设正方形ABCD的边长为 ,则
的半径为
在 中,
由圆周角定理得:
则
故答案为: .
三、解答题
11.【答案】 解:连接OA、OB,过点O作OH⊥AB于点H,即边心距n=OH,如图所示:
∴AH=HB,∠AOH=BOH,
∵六边形ABCDEF是正六边形,
∴∠AOB=60°,AB=BC=CD=DE=EF=AF=6cm,
∵OA=OB,
∴△AOB是等边三角形,
∴AH=3cm,∠AOH=30°,OA=AB=6cm,
∴ ,
∴ ,
∴ .
12.【答案】 解:如图,连接OA、OB、OC;
由题意知:∠BOA=∠COA= =60°,
∵OA=OB=OC,
∴△OAB、△OAC均为等边三角形,
∴∠BAO=∠CAO=60°,
= ;
=32 ,
∴阴影部分的面积=3× =64π﹣96 .
_21?????????è?????(www.21cnjy.com)_
