河南省卢氏一高2012届高三12月月考理科数学试题
文档属性
| 名称 | 河南省卢氏一高2012届高三12月月考理科数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 209.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-13 10:44:06 | ||
图片预览



文档简介
河南省卢氏一高2012届高三12月月考理科数学试题
第Ⅰ卷
一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.已知集合,集合,则、满足 ( )
A. B. C. D.且
2.已知单位向量满足,则夹角为 ( )
A. B. C. D.
3.已知,则的值为 ( )
A. B. C. D.
4.设是空间中两条不同的直线,α、β是两个不同的平面,则下列命题中正确的是( )
A.若, ,则
B.若, ,则
C.若,则
D.若,,则
5.“”是方程表示椭圆的 ( )
A.充分必要条件 B.充分但不必要条件
C.必要但不充分条件 D.既不充分也不必要条件
6.已知函数是定义域为的偶函数,且在上单调递增,则不等式
的解集为 ( )
A. B.
C. D.
7.由曲线围成的图形的面积等于 ( )
A. B. C. D.
8.已知函数为奇函数,该函数的部分图象如图所示,是边长为2的等边三角形,则的值为 ( )
A. B.
C. D.
9.过双曲线的焦点作渐近线的垂线,则直线与圆的位置关系是 ( )
A.相交 B.相离 C.相切 D.无法确定
10.若上是减函数,则实数b的取值范围是 ( )
A. B. C. D.
11.若x、y满足条件,且当x=y=3时,z =ax+y取最大值,则实数a的取值范围是( )
A.(-) B.(-∞,-)∪(,+∞)
C.() D.(-∞,-)∪(,+∞)
12.已知球O的半径为8,圆M和圆N为该球的两个小圆,AB为圆M与圆N的公共弦,若OM=ON=MN=6,则AB=( )
A.12 B.8 C.6 D.4
第Ⅱ卷
本卷包括必考题和选考题两部分。第13题~-第21题为必考题,每个试题考生都必须做答。第
22题~第24题为选考题,考生根据要求做答。
二、填空题:本大题共4小题,每小题5分。
13.在等比数列的值为 .
14.已知抛物线有相同的焦点F,点A是两曲线的交点,且AF轴,则双曲线的离心率为 .
15.不等式对恒成立,则x的取值范围是________________.
16.已知正方形ABCD边长为1,图形如示,点E为边BC的中点,
正方形内部一动点P满足:P到线段AD的距离等于P到点E
的距离,那么P点的轨迹与正方形的上、下底边及BC边
所围成平面图形的面积为_________.
三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)
设的内角的对边分别为,且,求:
(1)角的值;
(2)函数在区间上的最大值及对应的x值.
18.(本题满分12分)
已知数列,设,数列。
(1)求证:是等差数列;
(2)求数列的前n项和Sn.
19.(本小题满分12分)
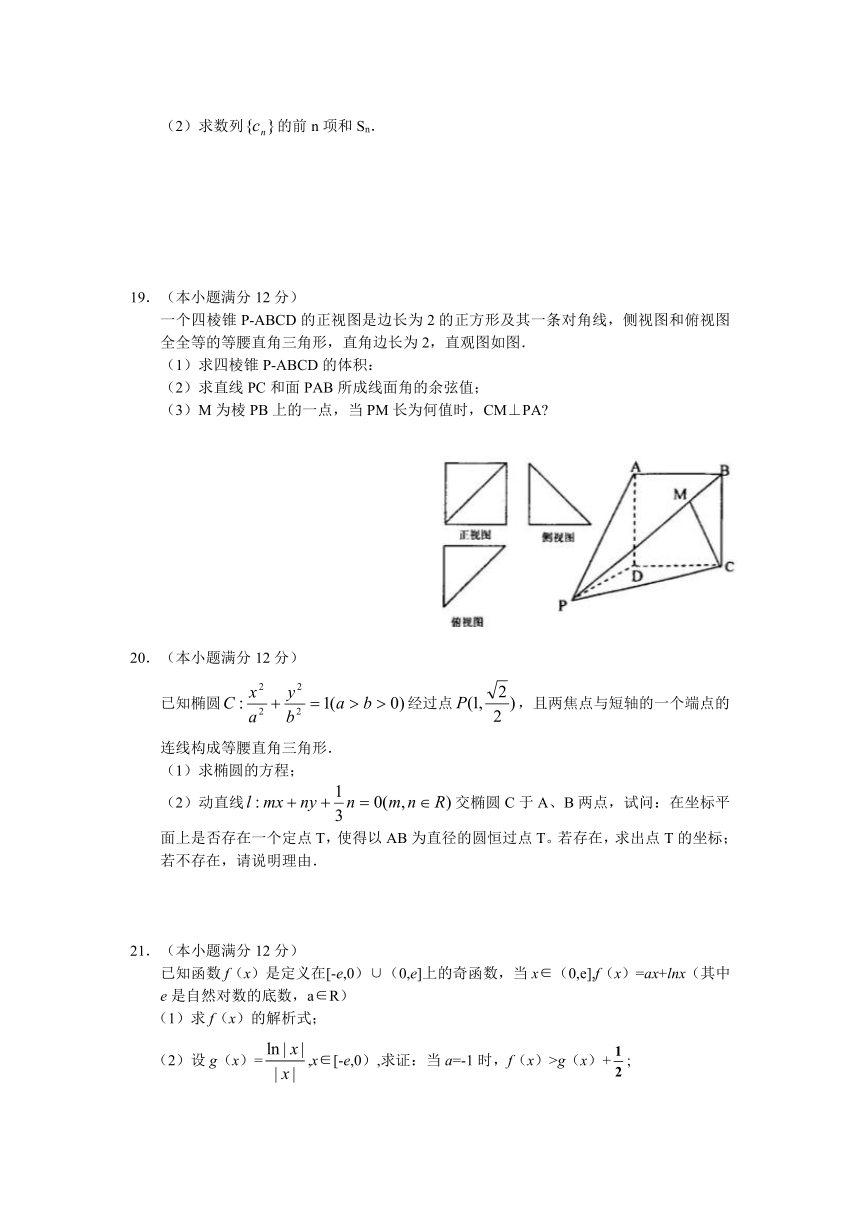
一个四棱锥P-ABCD的正视图是边长为2的正方形及其一条对角线,侧视图和俯视图全全等的等腰直角三角形,直角边长为2,直观图如图.
(1)求四棱锥P-ABCD的体积:
(2)求直线PC和面PAB所成线面角的余弦值;
(3)M为棱PB上的一点,当PM长为何值时,CM⊥PA
20.(本小题满分12分)
已知椭圆经过点,且两焦点与短轴的一个端点的连线构成等腰直角三角形.
(1)求椭圆的方程;
(2)动直线交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得以AB为直径的圆恒过点T。若存在,求出点T的坐标;若不存在,请说明理由.
21.(本小题满分12分)
已知函数f(x)是定义在[-e,0)∪(0,e]上的奇函数,当x∈(0,e],f(x)=ax+lnx(其中e是自然对数的底数,a∈R)
(1)求f(x)的解析式;
(2)设g(x)=,x∈[-e,0),求证:当a=-1时,f(x)>g(x)+;
(3)是否存在实数a,使得当x∈[-e,0)时f(x)的最小值是3 如果存在,求出实数a的值;如果不存在,请说明理由.
四、选考题(本小题满分10分)(请考生在22,23,24三题中任选一题做答,如果多做,则按所做的第一题记分.做答时用2B铅笔在答题卡把所选题目的题号涂黑)
22.选修4—1:几何证明选讲
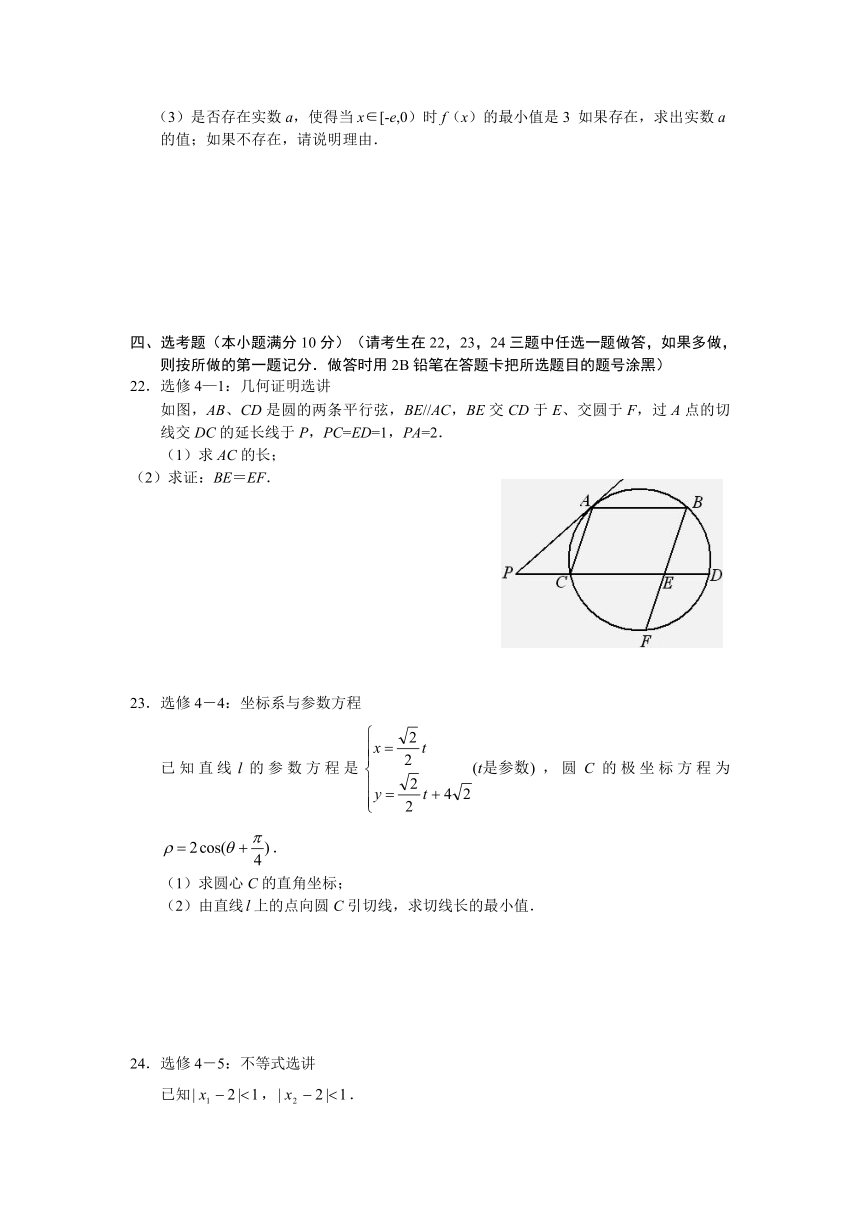
如图,AB、CD是圆的两条平行弦,BE//AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.
(1)求AC的长;
(2)求证:BE=EF.
23.选修4-4:坐标系与参数方程
已知直线的参数方程是,圆C的极坐标方程为.
(1)求圆心C的直角坐标;
(2)由直线上的点向圆C引切线,求切线长的最小值.
24.选修4-5:不等式选讲
已知,.
(1)求证:,;
(2)若,求证:.
参考答案
第Ⅰ卷(选择题,共60分)
一、选择题(本大题共12小题.每小题5分,共60分.在每小题给出的四个选项中。只有一项是符合题目要求的)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B C A D C D A D C C C B
二、填空题(本题共4个小题。每小题5分,共20分)
13.3 14. 15.x<-1或x> 16.
三、解答题(本题共6小题,总分70分.解答应写出文字说明,证明过程或演算步骤)
17.(1)sinA=2sinBcosC ∴sin(B-C)=0 ……………………(2分)
∴B=C ∵A= ∴B= ……………………(4分)
(2) ……………(6分)
∴ ……………(10分)
即时,f(x)达到最值值 ……………(12分)
18.(1)由已知 ∴bn=3n-2
∴bn-bn-1=3n-2-[3(n-1)-2]=3 (n≥2) ∴{bn}等差
(2)cn=anbn=
∴
19.(1)VP-ABCD=SABCD·PD=
(2)以D为坐标原点,建立 设为平面PAB的法向量
,PC与所成角,有
,PC与PAB所成角为
∴余弦值为
(3)由M在棱PB上,,得M()
即当|PM|=|PB|=时
CM⊥PA
20.(1)
(2)i)若n=0,
ii)若m=0,且过定点(0,1)
iii)m
设A(x1,y1),B(x2,y2),则以AB为直径的圆的方程为
(x-x1)(x-x2)+(y-y1)(y-y2)=0
∵
∴圆方程为:
将(0,1)代入显然成立,故存在T(0,1)符合题意。
21.
22.(本小题满分10分)
解:(I),, …………(2分)
又,
,, …………(4分)
, …………(5分)
(II),,而, …………(8分)
,. …………(10分)
23.(本小题满分10分)
解:(I),
, …………(2分)
, …………(3分)
即,.…………(5分)
(II)方法1:直线上的点向圆C 引切线长是
,
…………(8分)
∴直线上的点向圆C引的切线长的最小值是 …………(10分)
方法2:, …………(8分)
圆心C到距离是,
∴直线上的点向圆C引的切线长的最小值是 …………(10分)
24.(本小题满分10分)
证明:(I)∵,∴,即, …………(2分)
同理,∴, …………(4分)
∵,
∴; …………(5分)
(II),…………(8分)
∵,∴,
∴ …………(10分)
A
B
C
D
P
E
第Ⅰ卷
一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.已知集合,集合,则、满足 ( )
A. B. C. D.且
2.已知单位向量满足,则夹角为 ( )
A. B. C. D.
3.已知,则的值为 ( )
A. B. C. D.
4.设是空间中两条不同的直线,α、β是两个不同的平面,则下列命题中正确的是( )
A.若, ,则
B.若, ,则
C.若,则
D.若,,则
5.“”是方程表示椭圆的 ( )
A.充分必要条件 B.充分但不必要条件
C.必要但不充分条件 D.既不充分也不必要条件
6.已知函数是定义域为的偶函数,且在上单调递增,则不等式
的解集为 ( )
A. B.
C. D.
7.由曲线围成的图形的面积等于 ( )
A. B. C. D.
8.已知函数为奇函数,该函数的部分图象如图所示,是边长为2的等边三角形,则的值为 ( )
A. B.
C. D.
9.过双曲线的焦点作渐近线的垂线,则直线与圆的位置关系是 ( )
A.相交 B.相离 C.相切 D.无法确定
10.若上是减函数,则实数b的取值范围是 ( )
A. B. C. D.
11.若x、y满足条件,且当x=y=3时,z =ax+y取最大值,则实数a的取值范围是( )
A.(-) B.(-∞,-)∪(,+∞)
C.() D.(-∞,-)∪(,+∞)
12.已知球O的半径为8,圆M和圆N为该球的两个小圆,AB为圆M与圆N的公共弦,若OM=ON=MN=6,则AB=( )
A.12 B.8 C.6 D.4
第Ⅱ卷
本卷包括必考题和选考题两部分。第13题~-第21题为必考题,每个试题考生都必须做答。第
22题~第24题为选考题,考生根据要求做答。
二、填空题:本大题共4小题,每小题5分。
13.在等比数列的值为 .
14.已知抛物线有相同的焦点F,点A是两曲线的交点,且AF轴,则双曲线的离心率为 .
15.不等式对恒成立,则x的取值范围是________________.
16.已知正方形ABCD边长为1,图形如示,点E为边BC的中点,
正方形内部一动点P满足:P到线段AD的距离等于P到点E
的距离,那么P点的轨迹与正方形的上、下底边及BC边
所围成平面图形的面积为_________.
三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)
设的内角的对边分别为,且,求:
(1)角的值;
(2)函数在区间上的最大值及对应的x值.
18.(本题满分12分)
已知数列,设,数列。
(1)求证:是等差数列;
(2)求数列的前n项和Sn.
19.(本小题满分12分)
一个四棱锥P-ABCD的正视图是边长为2的正方形及其一条对角线,侧视图和俯视图全全等的等腰直角三角形,直角边长为2,直观图如图.
(1)求四棱锥P-ABCD的体积:
(2)求直线PC和面PAB所成线面角的余弦值;
(3)M为棱PB上的一点,当PM长为何值时,CM⊥PA
20.(本小题满分12分)
已知椭圆经过点,且两焦点与短轴的一个端点的连线构成等腰直角三角形.
(1)求椭圆的方程;
(2)动直线交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得以AB为直径的圆恒过点T。若存在,求出点T的坐标;若不存在,请说明理由.
21.(本小题满分12分)
已知函数f(x)是定义在[-e,0)∪(0,e]上的奇函数,当x∈(0,e],f(x)=ax+lnx(其中e是自然对数的底数,a∈R)
(1)求f(x)的解析式;
(2)设g(x)=,x∈[-e,0),求证:当a=-1时,f(x)>g(x)+;
(3)是否存在实数a,使得当x∈[-e,0)时f(x)的最小值是3 如果存在,求出实数a的值;如果不存在,请说明理由.
四、选考题(本小题满分10分)(请考生在22,23,24三题中任选一题做答,如果多做,则按所做的第一题记分.做答时用2B铅笔在答题卡把所选题目的题号涂黑)
22.选修4—1:几何证明选讲
如图,AB、CD是圆的两条平行弦,BE//AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.
(1)求AC的长;
(2)求证:BE=EF.
23.选修4-4:坐标系与参数方程
已知直线的参数方程是,圆C的极坐标方程为.
(1)求圆心C的直角坐标;
(2)由直线上的点向圆C引切线,求切线长的最小值.
24.选修4-5:不等式选讲
已知,.
(1)求证:,;
(2)若,求证:.
参考答案
第Ⅰ卷(选择题,共60分)
一、选择题(本大题共12小题.每小题5分,共60分.在每小题给出的四个选项中。只有一项是符合题目要求的)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B C A D C D A D C C C B
二、填空题(本题共4个小题。每小题5分,共20分)
13.3 14. 15.x<-1或x> 16.
三、解答题(本题共6小题,总分70分.解答应写出文字说明,证明过程或演算步骤)
17.(1)sinA=2sinBcosC ∴sin(B-C)=0 ……………………(2分)
∴B=C ∵A= ∴B= ……………………(4分)
(2) ……………(6分)
∴ ……………(10分)
即时,f(x)达到最值值 ……………(12分)
18.(1)由已知 ∴bn=3n-2
∴bn-bn-1=3n-2-[3(n-1)-2]=3 (n≥2) ∴{bn}等差
(2)cn=anbn=
∴
19.(1)VP-ABCD=SABCD·PD=
(2)以D为坐标原点,建立 设为平面PAB的法向量
,PC与所成角,有
,PC与PAB所成角为
∴余弦值为
(3)由M在棱PB上,,得M()
即当|PM|=|PB|=时
CM⊥PA
20.(1)
(2)i)若n=0,
ii)若m=0,且过定点(0,1)
iii)m
设A(x1,y1),B(x2,y2),则以AB为直径的圆的方程为
(x-x1)(x-x2)+(y-y1)(y-y2)=0
∵
∴圆方程为:
将(0,1)代入显然成立,故存在T(0,1)符合题意。
21.
22.(本小题满分10分)
解:(I),, …………(2分)
又,
,, …………(4分)
, …………(5分)
(II),,而, …………(8分)
,. …………(10分)
23.(本小题满分10分)
解:(I),
, …………(2分)
, …………(3分)
即,.…………(5分)
(II)方法1:直线上的点向圆C 引切线长是
,
…………(8分)
∴直线上的点向圆C引的切线长的最小值是 …………(10分)
方法2:, …………(8分)
圆心C到距离是,
∴直线上的点向圆C引的切线长的最小值是 …………(10分)
24.(本小题满分10分)
证明:(I)∵,∴,即, …………(2分)
同理,∴, …………(4分)
∵,
∴; …………(5分)
(II),…………(8分)
∵,∴,
∴ …………(10分)
A
B
C
D
P
E
同课章节目录
