7.2 探索直线平行的条件课件(共43张PPT)
文档属性
| 名称 | 7.2 探索直线平行的条件课件(共43张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-13 00:00:00 | ||
图片预览







文档简介
第七章 相交线与平行线
2 探索直线平行的条件
知识点一 同位角
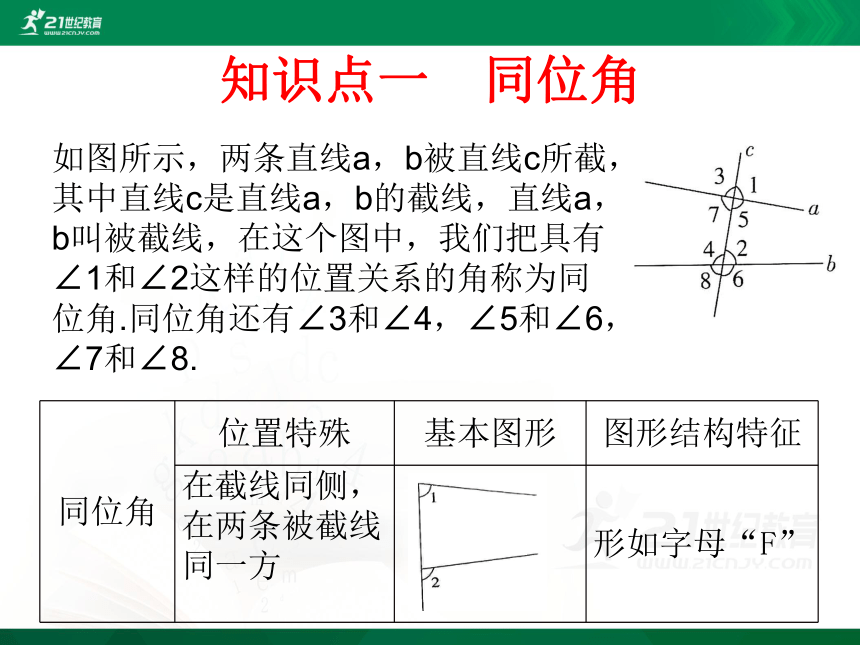
如图所示,两条直线a,b被直线c所截,
其中直线c是直线a,b的截线,直线a,
b叫被截线,在这个图中,我们把具有
∠1和∠2这样的位置关系的角称为同
位角.同位角还有∠3和∠4,∠5和∠6,
∠7和∠8.
同位角
位置特殊
基本图形
图形结构特征
在截线同侧,在两条被截线同一方
形如字母“F”
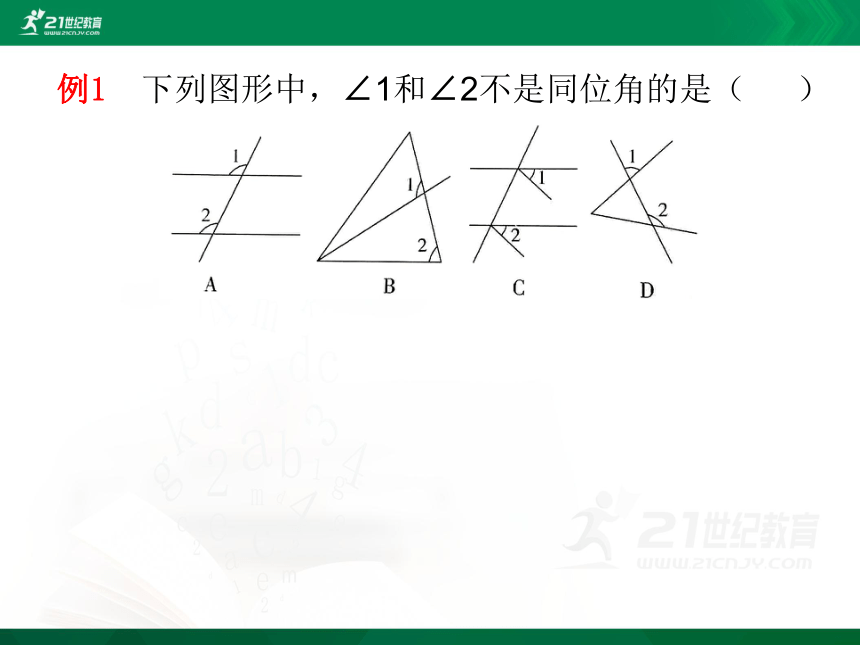
例1 下列图形中,∠1和∠2不是同位角的是( )
例1 下列图形中,∠1和∠2不是同位角的是( )
解析 根据同位角的概念可知,C选项中的∠1和∠2不是同位角.
例1 下列图形中,∠1和∠2不是同位角的是( )
解析 根据同位角的概念可知,C选项中的∠1和∠2不是同位角.
答案 C
知识点二 利用同位角判定两直线平行
文字语言
图形语言
符号语言
知识点二 利用同位角判定两直线平行
文字语言
图形语言
符号语言
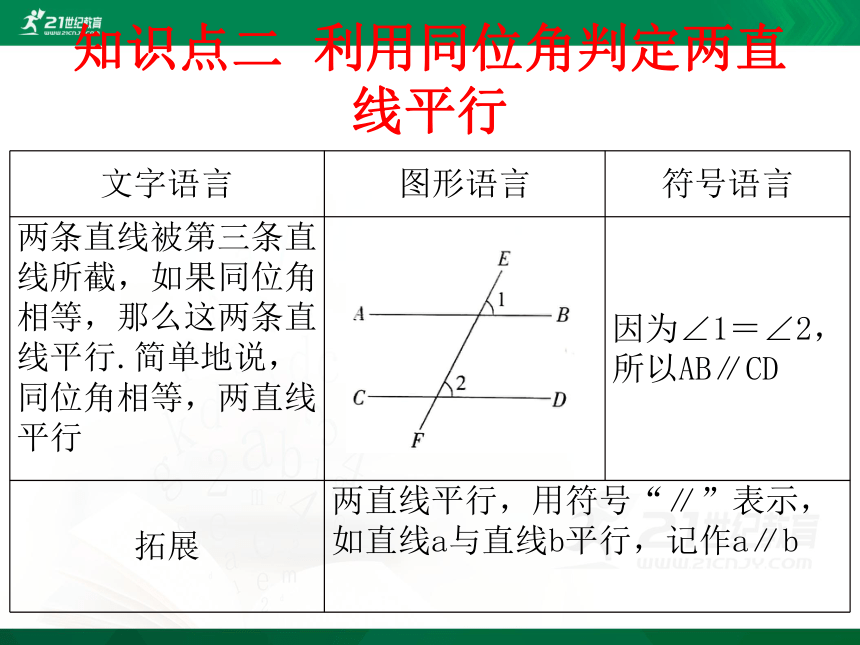
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单地说,同位角相等,两直线平行
因为∠1=∠2,所以AB∥CD
拓展
两直线平行,用符号“∥”表示,如直线a与直线b平行,记作a∥b
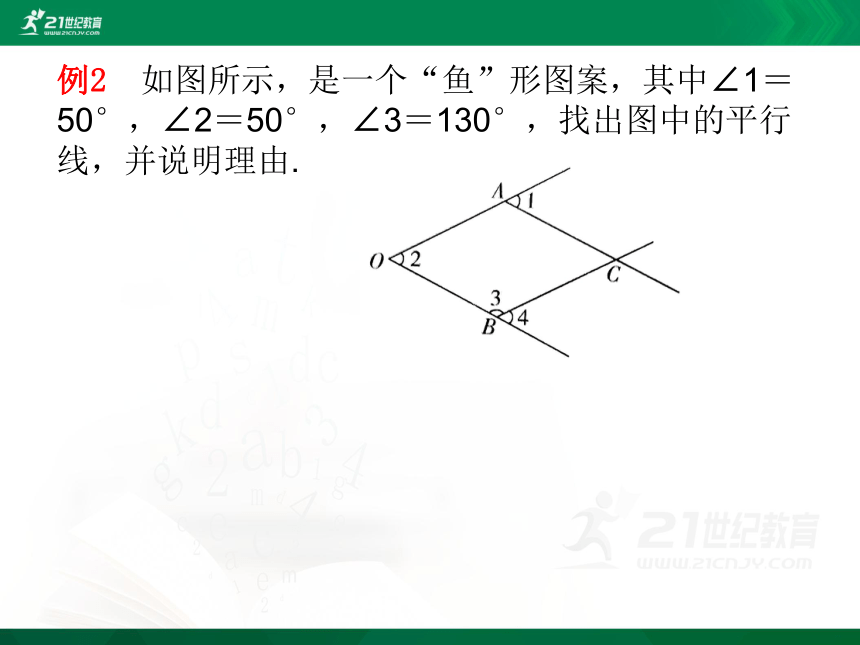
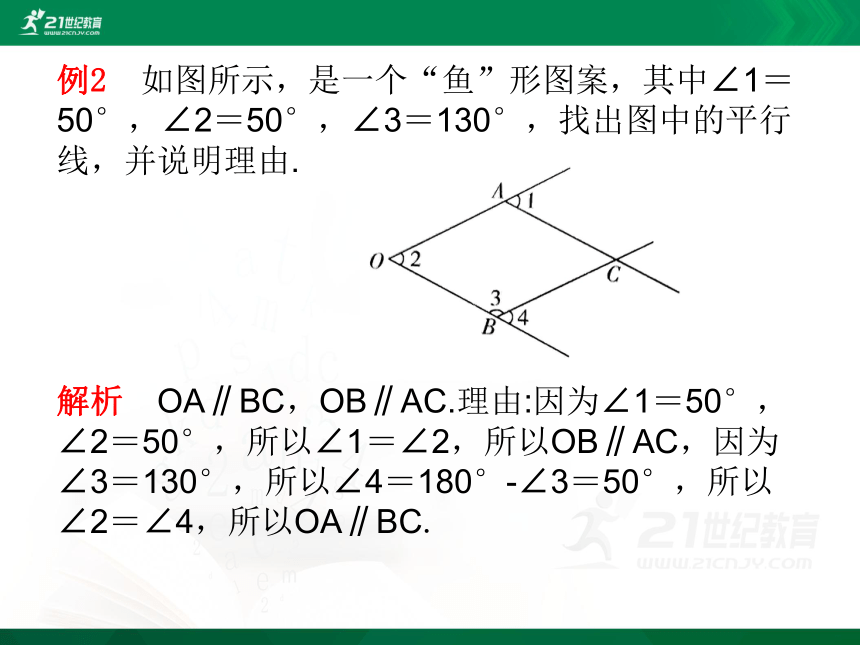
例2 如图所示,是一个“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.
例2 如图所示,是一个“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.
解析 OA∥BC,OB∥AC.理由:因为∠1=50°,∠2=50°,所以∠1=∠2,所以OB∥AC,因为∠3=130°,所以∠4=180°-∠3=50°,所以∠2=∠4,所以OA∥BC.
知识点 三平行线的基本事实及推论
平行线的基本事实
推论
内容
详解
知识点 三平行线的基本事实及推论
平行线的基本事实
推论
内容
经过直线外一点,有且只有一条直线与这条直线平行
平行于同一直线的两条直线平行
详解
(1)“有且只有”表示“存在”和“唯一”两重意思.(2)要强调“经过直线外一点”,若点在直线上,则不可能有平行线
如果b∥a,c∥a,那么b∥c
例3 下列说法中正确的有()
①一条直线的平行线只有一条;
②过一点与已知直线平行的直线只有一条;
③因为a∥b,c∥d,所以a∥d;
④经过直线外一点有且只有一条直线与已知直线平行.
A.1个 B.2个 C.3个 D.4个
例3 下列说法中正确的有()
①一条直线的平行线只有一条;
②过一点与已知直线平行的直线只有一条;
③因为a∥b,c∥d,所以a∥d;
④经过直线外一点有且只有一条直线与已知直线平行.
A.1个 B.2个 C.3个 D.4个
解析 一条直线的平行线有无数条,故①错误;②中的点的位置不明确,故②错误;③中b与c的位置关系不明确,故③错误;根据平行线的基本事实可知④正确.
例3 下列说法中正确的有()
①一条直线的平行线只有一条;
②过一点与已知直线平行的直线只有一条;
③因为a∥b,c∥d,所以a∥d;
④经过直线外一点有且只有一条直线与已知直线平行.
A.1个 B.2个 C.3个 D.4个
解析 一条直线的平行线有无数条,故①错误;②中的点的位置不明确,故②错误;③中b与c的位置关系不明确,故③错误;根据平行线的基本事实可知④正确.
答案 A
知识点四 内错角和同旁内角
内错角:
两个角都在两条被截线之间,并且在截线的两侧,具有这种位置关系的一组角叫做内错角.例如:图中的∠3与∠5,∠4与∠6.
同旁内角:
两个角都在两条被截线之间,并且在截线的同侧,具有这种位置关系的一组角叫做同旁内角.例如:图中的∠4与∠5,∠3与∠6.
知识点四 内错角和同旁内角
内错角和同旁内角的识别如下表:
角的名称
位置特征
基本图形
图形结构特征
内错角
同旁内角
知识点四 内错角和同旁内角
内错角和同旁内角的识别如下表:
角的名称
位置特征
基本图形
图形结构特征
内错角
在截线两侧,在
两条被截线之间
形如字母“Z”
同旁内角
在截线同侧,在
两条被截线之间
形如字母“U”
例4 指出图中的同位角、内错角、同旁内角.
例4 指出图中的同位角、内错角、同旁内角.
分析 为了便于确定哪两条直线被哪一条直线所截,应把组合图形分解成基本图形,即把复杂的图形用几个简单的图形表示出来.这样才能保证不重不漏地、准确地辨别同位角、内错角、同旁内角.可以将题图分解成如图所示的三个基本图形.
解析 原图形中共有两组同位角:∠DAE与∠C,∠BAE与∠C;共有两组内错角:∠BAD与∠B,∠B与∠BAE;共有四组同旁内角:∠CAD与∠C,∠B与∠C,∠B与∠BAC,∠C与∠BAC.
解析 原图形中共有两组同位角:∠DAE与∠C,∠BAE与∠C;共有两组内错角:∠BAD与∠B,∠B与∠BAE;共有四组同旁内角:∠CAD与∠C,∠B与∠C,∠B与∠BAC,∠C与∠BAC.
点拨 寻找一个角的同位角、内错角、同旁内角,首先,应该把这个角放在一个“三线八角”的基本图形中,其次,不管是同位角、内错角还是同旁内角,它们都具有一个共同特征:这两个角各有一边在同一直线上,这条共同的直线就是截线,而两个角剩下两边所在的直线就是两条被截线.
知识点五 利用内错角和同旁内角判定两直线平行
两条直线平行的判定
图例
符号语言
注意
知识点五 利用内错角和同旁内角判定两直线平行
两条直线平行的判定
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行,即内错角相等,两直线平行
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行,即同旁内角互补,两直线平行
图例
符号语言
如果∠1=∠2,
那么AB∥CD
如果∠3+∠4=180°,那么AB∥CD
注意
(1)准确识别三种角是判断两条直线平行的前提条件.
(2)确定两角的位置关系和数量关系
例5 如图所示,下列条件不能判定直线a∥b的是( )
A.∠1=∠2 B.∠1=∠3
C.∠1+∠4=180° D.∠2+∠4=180°
例5 如图所示,下列条件不能判定直线a∥b的是( )
A.∠1=∠2 B.∠1=∠3
C.∠1+∠4=180° D.∠2+∠4=180°
解析 A∵∠1=∠2,∴a∥b(内错角相等,两直线平行);B.∠1=∠3,∴a∥b(同位角相等,两直线平行);C.∠1+∠4=180°,与a,b的位置无关;D∵∠2+∠4=180°,∴a∥b(同旁内角互补,两直线平行).
例5 如图所示,下列条件不能判定直线a∥b的是( )
A.∠1=∠2 B.∠1=∠3
C.∠1+∠4=180° D.∠2+∠4=180°
解析 A∵∠1=∠2,∴a∥b(内错角相等,两直线平行);B.∠1=∠3,∴a∥b(同位角相等,两直线平行);C.∠1+∠4=180°,与a,b的位置无关;D∵∠2+∠4=180°,∴a∥b(同旁内角互补,两直线平行).
答案 C
经典例题
题型一 寻找图中的同位角、内错角和同旁内角
例1 根据下图填空:
(1)直线ED、BC被直线AB所截,∠1和_____是同位角;
(2)直线ED、BC被直线AF所截,∠3和_____是内错角;
(3)∠1和∠3是直线AB、AF被直线________所截形成的内错角;
(4)∠2和∠4是直线AB、_______被直线BC所截形成的______角.
题型一 寻找图中的同位角、内错角和同旁内角
解析(1)直线ED、BC被直线AB所截,∠1和∠2是同位角.(2)直线ED,BC被直线AF所截,∠3和∠4是内错角.(3)∠1和∠3是直线AB、AF被直线ED所截形成的内错角.(4)∠2和∠4是直线AB、AF被直线BC所截形成的同位角.
题型一 寻找图中的同位角、内错角和同旁内角
解析(1)直线ED、BC被直线AB所截,∠1和∠2是同位角.(2)直线ED,BC被直线AF所截,∠3和∠4是内错角.(3)∠1和∠3是直线AB、AF被直线ED所截形成的内错角.(4)∠2和∠4是直线AB、AF被直线BC所截形成的同位角.
答案(1)∠2(2)∠4(3)ED(4)AF;同位
题型一 寻找图中的同位角、内错角和同旁内角
解析(1)直线ED、BC被直线AB所截,∠1和∠2是同位角.(2)直线ED,BC被直线AF所截,∠3和∠4是内错角.(3)∠1和∠3是直线AB、AF被直线ED所截形成的内错角.(4)∠2和∠4是直线AB、AF被直线BC所截形成的同位角.
答案(1)∠2(2)∠4(3)ED(4)AF;同位
点拨 同位角、内错角和同旁内角可按下面的口诀来识别:一看三线,二找截线,三根据位置来分辨要结合图形,熟记同位角、内错角和同旁内角的位置特点,掌握它们的区别与联系.
题型二 平行线的判定及应用
例2 如图所示,有平面镜A与B,光线由水平方向射来,传播路线为a→b→c.已知a⊥b,b⊥c,∠1=∠3=45°,你知道平面镜A与B之间的位置关系吗?
题型二 平行线的判定及应用
例2 如图所示,有平面镜A与B,光线由水平方向射来,传播路线为a→b→c.已知a⊥b,b⊥c,∠1=∠3=45°,你知道平面镜A与B之间的位置关系吗?
分析 判断平面镜A与平面镜B是否平行,要看∠4和∠2是否相等,相等则平行,否则不平行.
解析 平面镜A与平面镜B互相平行.理由如下:如图所示,∵a⊥b,b⊥c,∴∠5=∠6=90°(垂直的定义)∴∠1+∠4=90°,∠2+∠3=90°(平角的定义)∵∠1=∠3=45°,∴∠4=∠2(等角的余角相等),∴平面镜A与平面镜B平行(内错角相等,两直线平行).
.
解析 平面镜A与平面镜B互相平行.理由如下:如图所示,∵a⊥b,b⊥c,∴∠5=∠6=90°(垂直的定义)∴∠1+∠4=90°,∠2+∠3=90°(平角的定义)∵∠1=∠3=45°,∴∠4=∠2(等角的余角相等),∴平面镜A与平面镜B平行(内错角相等,两直线平行).
点拨 对于实际问题,需先转化为数学问题,再根据已知条件解决问题.
题型三 在拐点处构造辅助线证明平行
例3 如图所示,平行线AB、CD被直线EF所截,过点B作BG⊥EF于点G,已知∠1=50°则∠B=( )
A.20° B.30° C.40° D.50°
解析 如图所示,过G点作GN∥CD,则∠2=∠1=50°.
因为BG⊥EF,所以∠BGF=90°,
所以∠3=∠BGF-∠2=90°-50°=40°,
因为AB∥CD,GN∥CD,所以AB∥GN,
所以∠B=∠3=40°.
解析 如图所示,过G点作GN∥CD,则∠2=∠1=50°.
因为BG⊥EF,所以∠BGF=90°,
所以∠3=∠BGF-∠2=90°-50°=40°,
因为AB∥CD,GN∥CD,所以AB∥GN,
所以∠B=∠3=40°.
答案 C
易错易混
易错点 由同位角、内错角、同旁内角反推“三线”时易错
例 如图所示,∠1与∠2,∠3与∠4是内错角,它们分别是由哪两条直线被
哪一条直线所截得到的?
错解 ∠1与∠2是由直线AD与BC被直线AC所截得到的,∠3与∠4是由直线AB与DC被直线BD所截得到的.
错解 ∠1与∠2是由直线AD与BC被直线AC所截得到的,∠3与∠4是由直线AB与DC被直线BD所截得到的.
正解 ∠1与∠2是由直线AB与DC被直线AC所截得到的,∠3与∠4是由直线AD与BC被直线BD所截得到的.
错解 ∠1与∠2是由直线AD与BC被直线AC所截得到的,∠3与∠4是由直线AB与DC被直线BD所截得到的.
正解 ∠1与∠2是由直线AB与DC被直线AC所截得到的,∠3与∠4是由直线AD与BC被直线BD所截得到的.
错因分析 错解中没有分清∠1与∠2,∠3与∠4分别是由哪两条直线被第三条直线所截得到的,从而导致答案错误.
2 探索直线平行的条件
知识点一 同位角
如图所示,两条直线a,b被直线c所截,
其中直线c是直线a,b的截线,直线a,
b叫被截线,在这个图中,我们把具有
∠1和∠2这样的位置关系的角称为同
位角.同位角还有∠3和∠4,∠5和∠6,
∠7和∠8.
同位角
位置特殊
基本图形
图形结构特征
在截线同侧,在两条被截线同一方
形如字母“F”
例1 下列图形中,∠1和∠2不是同位角的是( )
例1 下列图形中,∠1和∠2不是同位角的是( )
解析 根据同位角的概念可知,C选项中的∠1和∠2不是同位角.
例1 下列图形中,∠1和∠2不是同位角的是( )
解析 根据同位角的概念可知,C选项中的∠1和∠2不是同位角.
答案 C
知识点二 利用同位角判定两直线平行
文字语言
图形语言
符号语言
知识点二 利用同位角判定两直线平行
文字语言
图形语言
符号语言
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单地说,同位角相等,两直线平行
因为∠1=∠2,所以AB∥CD
拓展
两直线平行,用符号“∥”表示,如直线a与直线b平行,记作a∥b
例2 如图所示,是一个“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.
例2 如图所示,是一个“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.
解析 OA∥BC,OB∥AC.理由:因为∠1=50°,∠2=50°,所以∠1=∠2,所以OB∥AC,因为∠3=130°,所以∠4=180°-∠3=50°,所以∠2=∠4,所以OA∥BC.
知识点 三平行线的基本事实及推论
平行线的基本事实
推论
内容
详解
知识点 三平行线的基本事实及推论
平行线的基本事实
推论
内容
经过直线外一点,有且只有一条直线与这条直线平行
平行于同一直线的两条直线平行
详解
(1)“有且只有”表示“存在”和“唯一”两重意思.(2)要强调“经过直线外一点”,若点在直线上,则不可能有平行线
如果b∥a,c∥a,那么b∥c
例3 下列说法中正确的有()
①一条直线的平行线只有一条;
②过一点与已知直线平行的直线只有一条;
③因为a∥b,c∥d,所以a∥d;
④经过直线外一点有且只有一条直线与已知直线平行.
A.1个 B.2个 C.3个 D.4个
例3 下列说法中正确的有()
①一条直线的平行线只有一条;
②过一点与已知直线平行的直线只有一条;
③因为a∥b,c∥d,所以a∥d;
④经过直线外一点有且只有一条直线与已知直线平行.
A.1个 B.2个 C.3个 D.4个
解析 一条直线的平行线有无数条,故①错误;②中的点的位置不明确,故②错误;③中b与c的位置关系不明确,故③错误;根据平行线的基本事实可知④正确.
例3 下列说法中正确的有()
①一条直线的平行线只有一条;
②过一点与已知直线平行的直线只有一条;
③因为a∥b,c∥d,所以a∥d;
④经过直线外一点有且只有一条直线与已知直线平行.
A.1个 B.2个 C.3个 D.4个
解析 一条直线的平行线有无数条,故①错误;②中的点的位置不明确,故②错误;③中b与c的位置关系不明确,故③错误;根据平行线的基本事实可知④正确.
答案 A
知识点四 内错角和同旁内角
内错角:
两个角都在两条被截线之间,并且在截线的两侧,具有这种位置关系的一组角叫做内错角.例如:图中的∠3与∠5,∠4与∠6.
同旁内角:
两个角都在两条被截线之间,并且在截线的同侧,具有这种位置关系的一组角叫做同旁内角.例如:图中的∠4与∠5,∠3与∠6.
知识点四 内错角和同旁内角
内错角和同旁内角的识别如下表:
角的名称
位置特征
基本图形
图形结构特征
内错角
同旁内角
知识点四 内错角和同旁内角
内错角和同旁内角的识别如下表:
角的名称
位置特征
基本图形
图形结构特征
内错角
在截线两侧,在
两条被截线之间
形如字母“Z”
同旁内角
在截线同侧,在
两条被截线之间
形如字母“U”
例4 指出图中的同位角、内错角、同旁内角.
例4 指出图中的同位角、内错角、同旁内角.
分析 为了便于确定哪两条直线被哪一条直线所截,应把组合图形分解成基本图形,即把复杂的图形用几个简单的图形表示出来.这样才能保证不重不漏地、准确地辨别同位角、内错角、同旁内角.可以将题图分解成如图所示的三个基本图形.
解析 原图形中共有两组同位角:∠DAE与∠C,∠BAE与∠C;共有两组内错角:∠BAD与∠B,∠B与∠BAE;共有四组同旁内角:∠CAD与∠C,∠B与∠C,∠B与∠BAC,∠C与∠BAC.
解析 原图形中共有两组同位角:∠DAE与∠C,∠BAE与∠C;共有两组内错角:∠BAD与∠B,∠B与∠BAE;共有四组同旁内角:∠CAD与∠C,∠B与∠C,∠B与∠BAC,∠C与∠BAC.
点拨 寻找一个角的同位角、内错角、同旁内角,首先,应该把这个角放在一个“三线八角”的基本图形中,其次,不管是同位角、内错角还是同旁内角,它们都具有一个共同特征:这两个角各有一边在同一直线上,这条共同的直线就是截线,而两个角剩下两边所在的直线就是两条被截线.
知识点五 利用内错角和同旁内角判定两直线平行
两条直线平行的判定
图例
符号语言
注意
知识点五 利用内错角和同旁内角判定两直线平行
两条直线平行的判定
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行,即内错角相等,两直线平行
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行,即同旁内角互补,两直线平行
图例
符号语言
如果∠1=∠2,
那么AB∥CD
如果∠3+∠4=180°,那么AB∥CD
注意
(1)准确识别三种角是判断两条直线平行的前提条件.
(2)确定两角的位置关系和数量关系
例5 如图所示,下列条件不能判定直线a∥b的是( )
A.∠1=∠2 B.∠1=∠3
C.∠1+∠4=180° D.∠2+∠4=180°
例5 如图所示,下列条件不能判定直线a∥b的是( )
A.∠1=∠2 B.∠1=∠3
C.∠1+∠4=180° D.∠2+∠4=180°
解析 A∵∠1=∠2,∴a∥b(内错角相等,两直线平行);B.∠1=∠3,∴a∥b(同位角相等,两直线平行);C.∠1+∠4=180°,与a,b的位置无关;D∵∠2+∠4=180°,∴a∥b(同旁内角互补,两直线平行).
例5 如图所示,下列条件不能判定直线a∥b的是( )
A.∠1=∠2 B.∠1=∠3
C.∠1+∠4=180° D.∠2+∠4=180°
解析 A∵∠1=∠2,∴a∥b(内错角相等,两直线平行);B.∠1=∠3,∴a∥b(同位角相等,两直线平行);C.∠1+∠4=180°,与a,b的位置无关;D∵∠2+∠4=180°,∴a∥b(同旁内角互补,两直线平行).
答案 C
经典例题
题型一 寻找图中的同位角、内错角和同旁内角
例1 根据下图填空:
(1)直线ED、BC被直线AB所截,∠1和_____是同位角;
(2)直线ED、BC被直线AF所截,∠3和_____是内错角;
(3)∠1和∠3是直线AB、AF被直线________所截形成的内错角;
(4)∠2和∠4是直线AB、_______被直线BC所截形成的______角.
题型一 寻找图中的同位角、内错角和同旁内角
解析(1)直线ED、BC被直线AB所截,∠1和∠2是同位角.(2)直线ED,BC被直线AF所截,∠3和∠4是内错角.(3)∠1和∠3是直线AB、AF被直线ED所截形成的内错角.(4)∠2和∠4是直线AB、AF被直线BC所截形成的同位角.
题型一 寻找图中的同位角、内错角和同旁内角
解析(1)直线ED、BC被直线AB所截,∠1和∠2是同位角.(2)直线ED,BC被直线AF所截,∠3和∠4是内错角.(3)∠1和∠3是直线AB、AF被直线ED所截形成的内错角.(4)∠2和∠4是直线AB、AF被直线BC所截形成的同位角.
答案(1)∠2(2)∠4(3)ED(4)AF;同位
题型一 寻找图中的同位角、内错角和同旁内角
解析(1)直线ED、BC被直线AB所截,∠1和∠2是同位角.(2)直线ED,BC被直线AF所截,∠3和∠4是内错角.(3)∠1和∠3是直线AB、AF被直线ED所截形成的内错角.(4)∠2和∠4是直线AB、AF被直线BC所截形成的同位角.
答案(1)∠2(2)∠4(3)ED(4)AF;同位
点拨 同位角、内错角和同旁内角可按下面的口诀来识别:一看三线,二找截线,三根据位置来分辨要结合图形,熟记同位角、内错角和同旁内角的位置特点,掌握它们的区别与联系.
题型二 平行线的判定及应用
例2 如图所示,有平面镜A与B,光线由水平方向射来,传播路线为a→b→c.已知a⊥b,b⊥c,∠1=∠3=45°,你知道平面镜A与B之间的位置关系吗?
题型二 平行线的判定及应用
例2 如图所示,有平面镜A与B,光线由水平方向射来,传播路线为a→b→c.已知a⊥b,b⊥c,∠1=∠3=45°,你知道平面镜A与B之间的位置关系吗?
分析 判断平面镜A与平面镜B是否平行,要看∠4和∠2是否相等,相等则平行,否则不平行.
解析 平面镜A与平面镜B互相平行.理由如下:如图所示,∵a⊥b,b⊥c,∴∠5=∠6=90°(垂直的定义)∴∠1+∠4=90°,∠2+∠3=90°(平角的定义)∵∠1=∠3=45°,∴∠4=∠2(等角的余角相等),∴平面镜A与平面镜B平行(内错角相等,两直线平行).
.
解析 平面镜A与平面镜B互相平行.理由如下:如图所示,∵a⊥b,b⊥c,∴∠5=∠6=90°(垂直的定义)∴∠1+∠4=90°,∠2+∠3=90°(平角的定义)∵∠1=∠3=45°,∴∠4=∠2(等角的余角相等),∴平面镜A与平面镜B平行(内错角相等,两直线平行).
点拨 对于实际问题,需先转化为数学问题,再根据已知条件解决问题.
题型三 在拐点处构造辅助线证明平行
例3 如图所示,平行线AB、CD被直线EF所截,过点B作BG⊥EF于点G,已知∠1=50°则∠B=( )
A.20° B.30° C.40° D.50°
解析 如图所示,过G点作GN∥CD,则∠2=∠1=50°.
因为BG⊥EF,所以∠BGF=90°,
所以∠3=∠BGF-∠2=90°-50°=40°,
因为AB∥CD,GN∥CD,所以AB∥GN,
所以∠B=∠3=40°.
解析 如图所示,过G点作GN∥CD,则∠2=∠1=50°.
因为BG⊥EF,所以∠BGF=90°,
所以∠3=∠BGF-∠2=90°-50°=40°,
因为AB∥CD,GN∥CD,所以AB∥GN,
所以∠B=∠3=40°.
答案 C
易错易混
易错点 由同位角、内错角、同旁内角反推“三线”时易错
例 如图所示,∠1与∠2,∠3与∠4是内错角,它们分别是由哪两条直线被
哪一条直线所截得到的?
错解 ∠1与∠2是由直线AD与BC被直线AC所截得到的,∠3与∠4是由直线AB与DC被直线BD所截得到的.
错解 ∠1与∠2是由直线AD与BC被直线AC所截得到的,∠3与∠4是由直线AB与DC被直线BD所截得到的.
正解 ∠1与∠2是由直线AB与DC被直线AC所截得到的,∠3与∠4是由直线AD与BC被直线BD所截得到的.
错解 ∠1与∠2是由直线AD与BC被直线AC所截得到的,∠3与∠4是由直线AB与DC被直线BD所截得到的.
正解 ∠1与∠2是由直线AB与DC被直线AC所截得到的,∠3与∠4是由直线AD与BC被直线BD所截得到的.
错因分析 错解中没有分清∠1与∠2,∠3与∠4分别是由哪两条直线被第三条直线所截得到的,从而导致答案错误.
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
