第27章 圆 单元测试卷(含解析)
图片预览

文档简介
中小学教育资源及组卷应用平台
初中数学华师大版九年级下学期 第27章测试卷
一、单选题
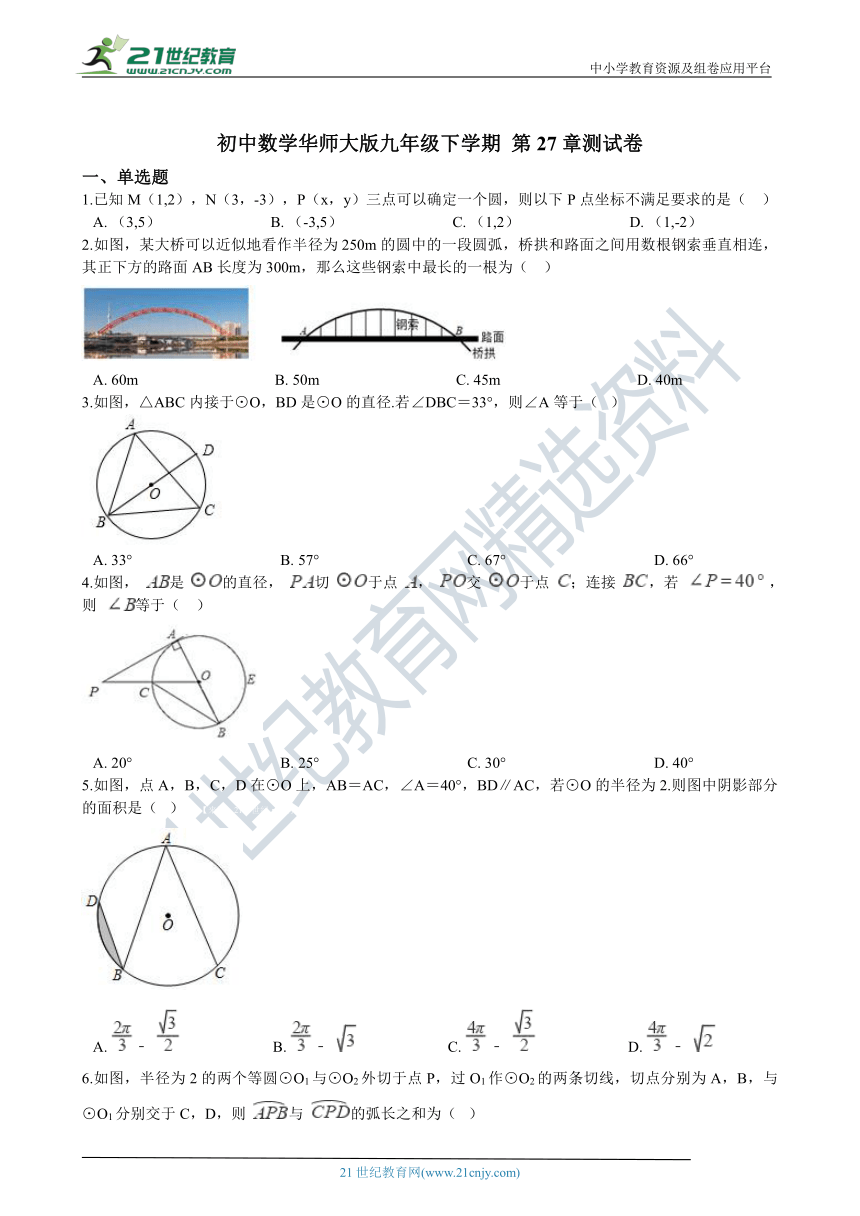
1.已知M(1,2),N(3,-3),P(x,y)三点可以确定一个圆,则以下P点坐标不满足要求的是(?? )
A.?(3,5)?????????????????????????????B.?(-3,5)?????????????????????????????C.?(1,2)?????????????????????????????D.?(1,-2)
2.如图,某大桥_??????è???????°???_作半径为250m的圆中的一段圆弧,桥拱和路面之间用数根钢索垂直相连,其正下方的路面AB长度为300m,那么这些钢索中最长的一根为(?? ) 21世纪教育网版权所有
A.?60m????????????????????????????????????B.?50m????????????????????????????????????C.?45m????????????????????????????????????D.?40m
3.如图,△ABC内接于⊙O,BD是⊙O的直径.若∠DBC=33°,则∠A等于(? )
A.?33°???????????????????????????????????????B.?57°???????????????????????????????????????C.?67°???????????????????????????????????????D.?66°
4.如图, 是 的直径, 切 于点 , 交 于点 ;连接 ,若 ,则 等于(?? ) 21·cn·jy·com
A.?20°???????????????????????????????????????B.?25°???????????????????????????????????????C.?30°???????????????????????????????????????D.?40°
5.如图,点A,B,C,D在⊙O上,AB=AC,∠A=40°,BD∥AC,若⊙O的半径为2.则图中阴影部分的面积是(? ) 【来源:21·世纪·教育·网】
A.?﹣ ????????????????????????B.?﹣ ????????????????????????C.?﹣ ????????????????????????D.?﹣
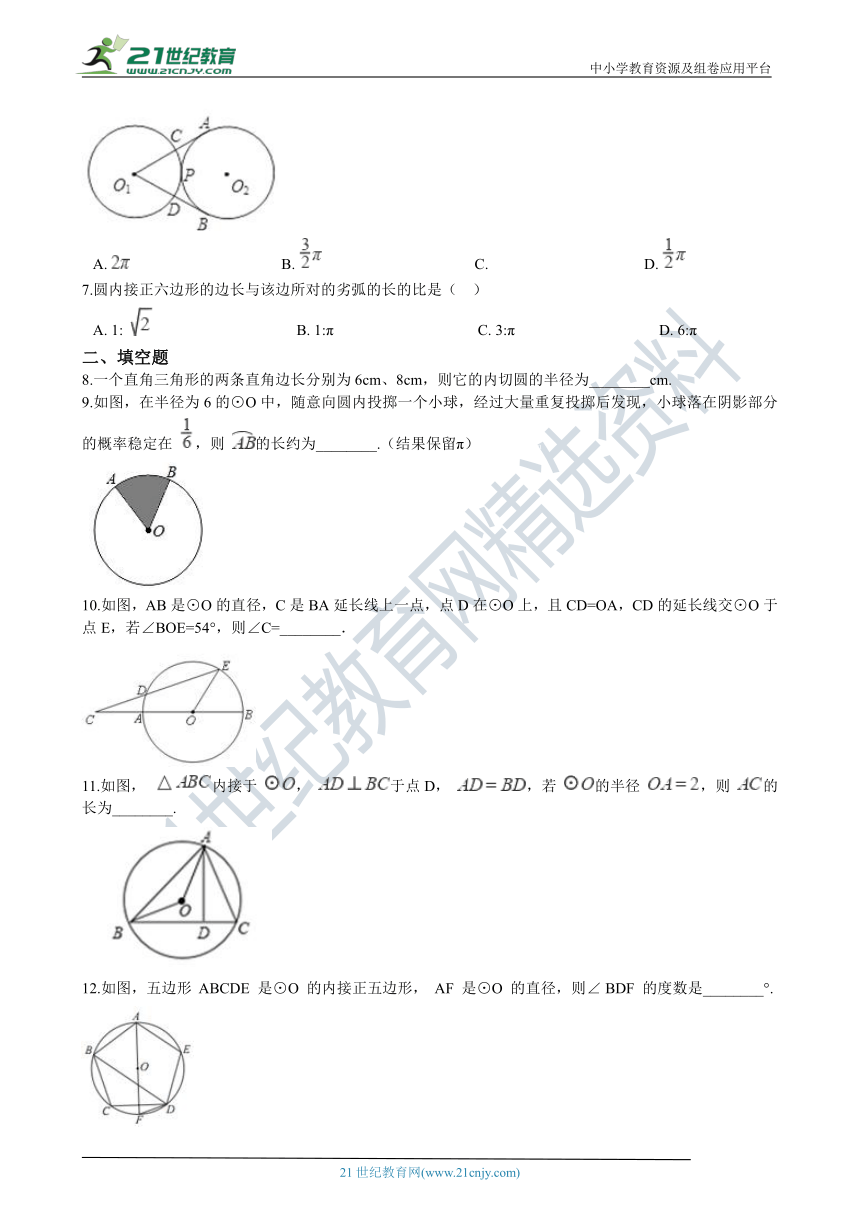
6.如图,半径为2的两个等圆⊙O1与⊙O2外切于点P,过O1作⊙O2的两条切线,切点分别为A,B,与⊙O1分别交于C,D,则 与 的弧长之和为(? ) 【出处:21教育名师】
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?
7.圆内接正六边形的边长与该边所对的劣弧的长的比是(?? )
A.?1: ??????????????????????????????????????B.?1:π??????????????????????????????????????C.?3:π??????????????????????????????????????D.?6:π
二、填空题
8.一个直角三角形的两条直角边长分别为6cm、8cm,则它的内切圆的半径为________cm.
9.如图,在半径为6的⊙O中,随意向圆内投掷一个小球,经过大量重复投掷后发现,小球落在阴影部分的概率稳定在 ,则 的长约为________.(结果保留π) 21*cnjy*com
10.如图,AB是⊙O的直径,_C???BA???é??_线上一点,点D在⊙O上,且CD=OA,CD的延长线交⊙O于点E,若∠BOE=54°,则∠C=________.
11.如图, 内接于 , 于点D, ,若 的半径 ,则 的长为________.
12.如图,五边形 ABCDE 是⊙O 的内接正五边形, AF 是⊙O 的直径,则∠ BDF 的度数是________°.
三、解答题
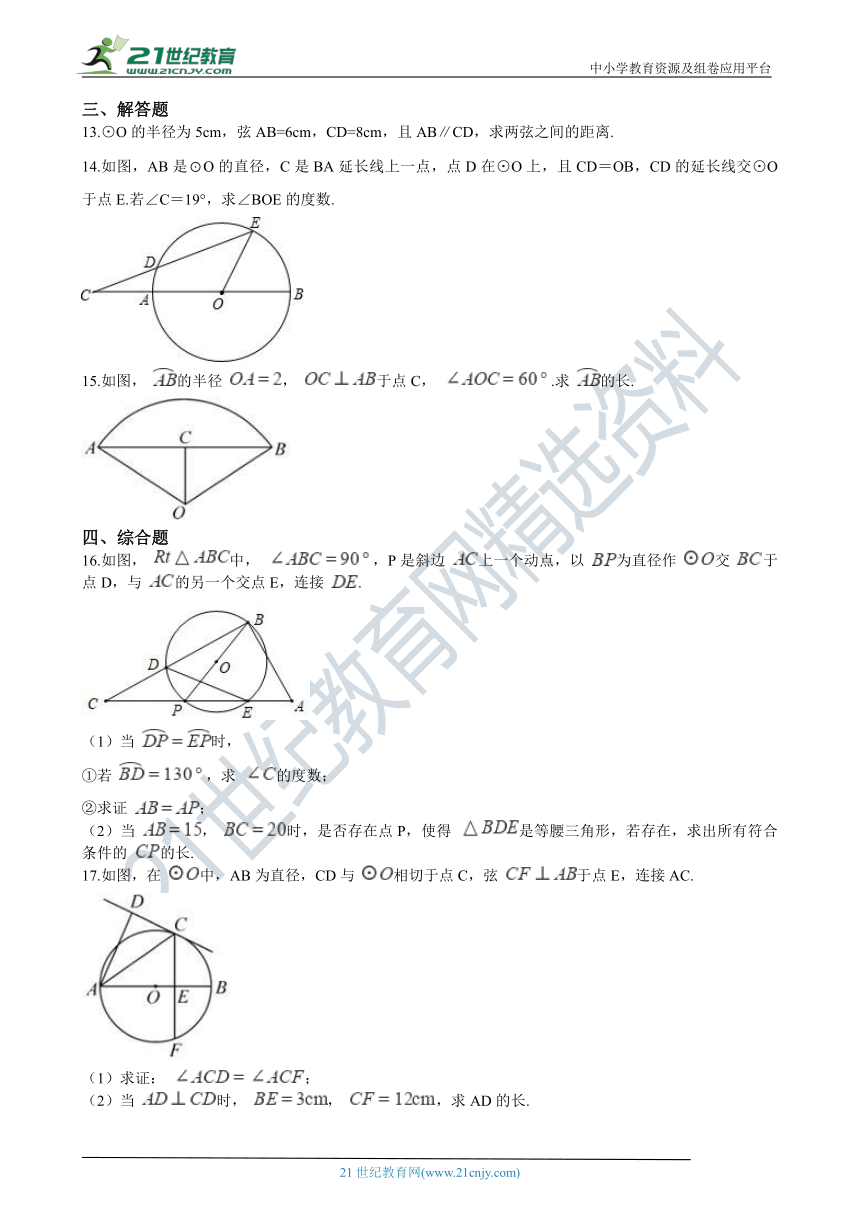
13.⊙O的半径为5cm,弦AB=6cm,CD=8cm,且AB∥CD,求两弦之间的距离.
14.如图,A_B??????O??????_径,C是BA延长线上一点,点D在⊙O上,且CD=OB,CD的延长线交⊙O于点E.若∠C=19°,求∠BOE的度数.???
15.如图, 的半径 , 于点C, .求 的长.
四、综合题
16.如图, 中, ,P是斜边 上一个动点,以 为直径作 交 于点D,与 的另一个交点E,连接 .
(1)当 时,
①若 ,求 的度数;
②求证 ;
(2)当 , 时,是否存在点P,使得 是等腰三角形,若存在,求出所有符合条件的 的长.
17.如图,在 中,AB为直径,CD与 相切于点C,弦 于点E,连接AC.
(1)求证: ;
(2)当 时, , ,求AD的长.
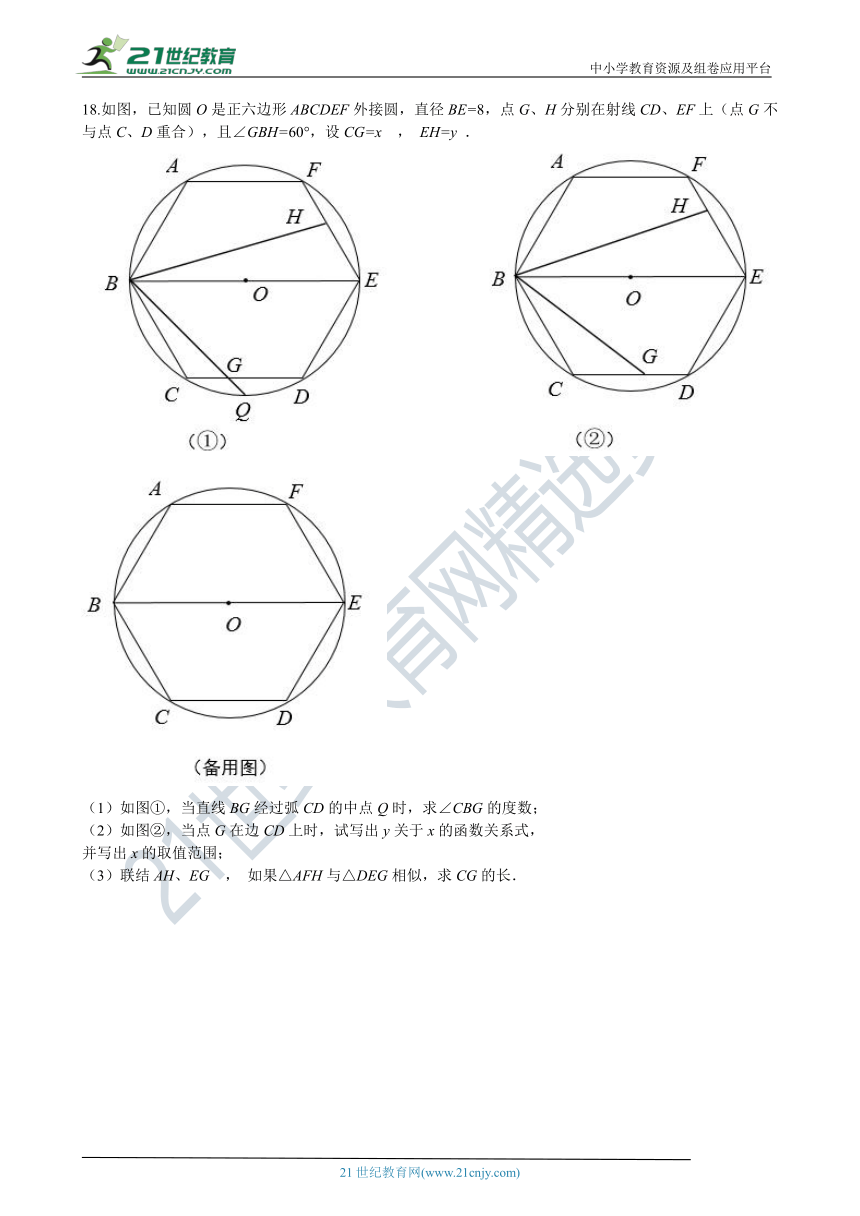
18.如图,已知圆O是正_???è?????ABC_DEF外接圆,直径BE=8,点G、H分别在射线CD、EF上(点G不与点C、D重合),且∠GBH=60°,设CG=x , EH=y . 21·世纪*教育网
(1)如图①,当直线BG经过弧CD的中点Q时,求∠CBG的度数;
(2)如图②,当点G在边CD上时,试写出y关于x的函数关系式,
并写出x的取值范围;
(3)联结AH、EG , 如果△AFH与△DEG相似,求CG的长.
答案解析部分
一、单选题
1.【答案】 C
解:设直线MN的解析式为y=kx+b,
∴,
解得,
∴y=-x+,
当x=3时,y=-3≠5;当x=-3时,y=12;当x=13时,y=2≠-2;
∴点C在直线MN上,该三点不能构成圆.
故答案为:C.
2.【答案】 B
解:设弧AB的圆心为点O,过点O作OC⊥AB于点D,交弧AB于点C,
∴AD=AB=×300=150,
∵OC=OA=250
在Rt△AOD中
;
∴这些钢索中_???é??????????????_CD=OC-DO=250-200=50.
故答案为:B.
3.【答案】 B
解:如图,连接DC,
∵BD是⊙O的直径,
∴∠BCD=90°,
∴∠D=180-∠BCD-∠DBC=180°-90°-33°=57°,
又∵∠A=∠D,
∴∠A=57°.
故答案为:B.
4.【答案】 B
解: 切 于点 ,
故答案为:B.
5.【答案】 B
解:如图所示,连接BC、OD、OB,
∵∠A=40°,AB=AC,
∴∠ACB=70°,
∵BD∥AC,
∴∠ABD=∠A=40°,
∴∠ACD=∠ABD=40°,
∴∠BCD=30°,
则∠BOD=2∠BCD=60°,
又OD=OB,
∴△BOD是等边三角形,
则图中阴影部分的面积是S扇形BOD﹣S△BOD
= ﹣ ×22
= π﹣ ,
故答案为:B.
6.【答案】 A
解:连接OA、OB
∵O1A和O1B与⊙O2相切
∴∠O1AO2=∠O1BO2=90°
∴∠AO1B+∠AO2B=360°-(∠O1AO2+∠O1BO2)=180°
∴ 与 的弧长之和为
=
=
=
故答案为:A.
7.【答案】 C
解:整理变形的中心角为 =60°,
设正六边形的半径为r,
则其边长为r,
边长所对的弧长为: ,
∴正六边形的边长和边长所对的弧长的比为:r: =3: .
故答案为:C.
二、填空题
8.【答案】 2
解:因为直角三角形两条直角边长分别为6cm,8cm,所以该直角三角形的斜边长为10cm,
则这个三角形的内切圆的半径= =2(cm).
故答案为:2.
9.【答案】 2π
解:∵圆的半径为6,
∴面积为36π,
∵大量重复投掷后发现,小球落在阴影部分的概率稳定在 ,
∴扇形的面积为 =6π,
设扇形的弧长为l,则 l×3=6π,
解得:l=2π,
∴ 的长约为2π,
故答案为:2π.
10.【答案】 18°
解:连接OD,
∵CD=OA=OD,
∴∠C=∠DOC,
∴∠ODE=∠C+∠DOC=2∠C,
∵OD=OE,
∴∠E=∠EDO=2∠C,
∴∠EOB=∠C+∠E=3∠C=54°,
∴∠C=18°,
故答案为:18°.
11.【答案】
解:延长AO交圆于E点,
∵△ADB为等腰直角三角形,
∴AB:AD=,
∵OA=2,∴AE=4,
∵AE为直径,
∴∠ABE=90°,
∴∠ABE=∠ADC,
∵∠E和∠C所对的弧都为AB弧,
∴∠E=∠C,
∴AE:AC=AB:AD,
∴4:AC=,
∴AC=2.
故答案为: .
12.【答案】 54
解:连接AD,
∵AF是⊙O的直径,
∴∠ADF=90°,
∵五边形ABCDE是⊙O的内接正五边形,
∴∠ABC=∠C=108°,
∴∠ABD=72°,
∴∠F=∠ABD=72°,
∴∠FAD=18°,
∴∠CDF=∠DAF=18°,
∴∠BDF=36°+18°=54°,
故答案为:54.
三、解答题
13.【答案】 解:如图:过点O作OE⊥AB于E,交CD于F,
∵AB∥CD,
∴OF⊥CD,
∵OE过圆心,OE⊥AB,
∴EB= AB=3cm,
∵OB=5cm,
∴EO=4cm,
同理,OF=3cm,
∴EF=4-3=1cm,
当AB、CD位于圆心两旁时EF=4+3=7cm,
∴EF=1cm或EF=7cm.
14.【答案】 解:连接OD,
∵CD=OB=OD,∠C=19°,∴∠ODE=2∠C=38°,∵OD=OE,
∴∠E=∠EDO=38°,∴∠EOB=∠C+∠E=19°+38°=57°
15.【答案】 解:∵OC⊥AB,∠AOC=60°,
∴∠AOB=120°.
∵OA=2,
∴ 的长为:=.
四、综合题
16.【答案】 (1)解:①如图,连接PD,
∵PB为直径,
∴∠PDB=90°,
∠BPD=65°,
∴∠PBD=90°-∠BPD=25°,
∵ ,
∴ ,
∴,
∴∠C=∠BPE-∠PBD=65°-25°=40°;
②?证明:∵,
∴∠CBP=∠EBP,
∵∠ABE+∠A=∠C+∠A=90°,
∴∠C=∠ABE,
∴∠ABP=∠ABE+∠EBP,∠APB=∠C+∠CBP,
∴∠ABP=∠APB,
∴AP=AB;
(2)解:存在,
如图,连接PD,
由AB=15,BC= 20,
由勾股定理得: AC===25,
∵AB.BC=AC.BE ,
即×15×20=×25×BE,
∴ BE=12,
∵BP是直径,
∴∠PDB =90° ,
∵∠ABC =90° ,
∴PD∥AB ,
∴△DCP∽△BCA ,
∴,
∴,
△BDE是等腰角形,分三种情况:
当BD= BE时,BD=BE=12,
∴CD=BC-BD=20-12=8,
∴ CP=CD=x8=10,
当BD= ED时,可知点D是Rt△CBE斜边的中线,
∴CD=BC=10,
∴CP=CD=×10=,
当DE=BE时,作EH⊥BC, 则H是BD中点,EH//AB, 如图,
AE===9,
:.CE=AC-AE=25-9=16, CH=BC-BH=20-BH ,
∵EH∥AB,
∴,
即,
解得: BH=,
∴BD=2BH=,
∴CD= BC-BD=20-=,
∴CP=CD=,
综上所述,△BDE 是等腰三角形,符合条件的CP的长为10或或7.
17.【答案】 (1)证明:连接OC,
∵CD切??于点C,
∴∠OCD=90°,
∴∠ACD+∠ACO=90°.
∵CF⊥AB,
∴∠AEC=90°,
∴∠ACF+∠CAE=90°.
∵OA=OC,
∴∠ACO=∠CAE,
∴∠ACD=∠ACF.
(2)解:由(1)可知,∠ACD=∠ACF.
∵CF⊥AB,CF=12,
∴CE=CF=6.
设?的半径为r,则OE=r-3.
在Rt△OEC中,OC2=OE2+CE2 , 即r2=(r-3)2+62 ,
解得r=,
∴AE=AB-BE=15-3=12.
∵∠ACD=∠ACF,AD⊥CD,CF⊥AB,
∴AD=AE=12(cm).
18.【答案】 (1)解:如图①,联结OQ.
∵正六边形ABCDEF,∴BC=DE,∠ABC=120°.
∴ ,∠EBC= ∠ABC=60°.
∵点Q是 的中点, ∴ ∴ , 即 . ∴∠BOQ=∠EOQ, 又∵∠BOQ+∠EOQ=180°,
∴∠BOQ=∠EOQ=90°.
又∵BO=OQ,∴∠OBQ=∠BQO=45°, ∴∠CBG=60° 45°=15°.
(2)解:如图②,在BE上截取EM=HE,联结HM.
∵正六边形ABCDEF,直径BE=8, ∴BO=OE=BC=4,∠C=∠FED=120°,
∴∠FEB= ∠FED=60°.
∵EM=HE,EH=y,
∴EM=HE=HM=y,∠HME=60°,
∴∠C=∠HMB=120°.
∵∠EBC=∠GBH=60°, ∴∠EBC ∠GBE=∠EBC ∠GBE, 即∠HBE=∠GBC. ∴△BCG∽△BMH,∴ .
又∵CG= x,BE=8,BC=4,∴ ,
∴y与x的函数关系式为 ( )
(3)解:如图③,当点G在边CD上时.
由于△AFH∽△EDG,且∠CDE=∠AFE=120°, ① 当 .∵AF=ED,∴FH=DG, 即: ,解分式方程得 . 经检验 是原方程的解,但不符合题意舍去. ② 当 .即: ,解分式方程得 . 经检验 是原方程的解,但不符合题意舍去. 2-1-c-n-j-y
如图④,当点G在CD的延长线上时.
由于△AFH∽△EDG,且∠EDG=∠AFH=60°,
① 当 .∵AF=ED,∴FH=DG, 即: ,解分式方程得 . 经检验 是原方程的解,但不符合题意舍去. ② 当 .即: ,解分式方程得 . 经检验 是原方程的解,且符合题意. 21cnjy.com
∴综上所述,如果△AFH与△DEG相似,那么CG的长为12.
_21?????????è?????(www.21cnjy.com)_
初中数学华师大版九年级下学期 第27章测试卷
一、单选题
1.已知M(1,2),N(3,-3),P(x,y)三点可以确定一个圆,则以下P点坐标不满足要求的是(?? )
A.?(3,5)?????????????????????????????B.?(-3,5)?????????????????????????????C.?(1,2)?????????????????????????????D.?(1,-2)
2.如图,某大桥_??????è???????°???_作半径为250m的圆中的一段圆弧,桥拱和路面之间用数根钢索垂直相连,其正下方的路面AB长度为300m,那么这些钢索中最长的一根为(?? ) 21世纪教育网版权所有
A.?60m????????????????????????????????????B.?50m????????????????????????????????????C.?45m????????????????????????????????????D.?40m
3.如图,△ABC内接于⊙O,BD是⊙O的直径.若∠DBC=33°,则∠A等于(? )
A.?33°???????????????????????????????????????B.?57°???????????????????????????????????????C.?67°???????????????????????????????????????D.?66°
4.如图, 是 的直径, 切 于点 , 交 于点 ;连接 ,若 ,则 等于(?? ) 21·cn·jy·com
A.?20°???????????????????????????????????????B.?25°???????????????????????????????????????C.?30°???????????????????????????????????????D.?40°
5.如图,点A,B,C,D在⊙O上,AB=AC,∠A=40°,BD∥AC,若⊙O的半径为2.则图中阴影部分的面积是(? ) 【来源:21·世纪·教育·网】
A.?﹣ ????????????????????????B.?﹣ ????????????????????????C.?﹣ ????????????????????????D.?﹣
6.如图,半径为2的两个等圆⊙O1与⊙O2外切于点P,过O1作⊙O2的两条切线,切点分别为A,B,与⊙O1分别交于C,D,则 与 的弧长之和为(? ) 【出处:21教育名师】
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?
7.圆内接正六边形的边长与该边所对的劣弧的长的比是(?? )
A.?1: ??????????????????????????????????????B.?1:π??????????????????????????????????????C.?3:π??????????????????????????????????????D.?6:π
二、填空题
8.一个直角三角形的两条直角边长分别为6cm、8cm,则它的内切圆的半径为________cm.
9.如图,在半径为6的⊙O中,随意向圆内投掷一个小球,经过大量重复投掷后发现,小球落在阴影部分的概率稳定在 ,则 的长约为________.(结果保留π) 21*cnjy*com
10.如图,AB是⊙O的直径,_C???BA???é??_线上一点,点D在⊙O上,且CD=OA,CD的延长线交⊙O于点E,若∠BOE=54°,则∠C=________.
11.如图, 内接于 , 于点D, ,若 的半径 ,则 的长为________.
12.如图,五边形 ABCDE 是⊙O 的内接正五边形, AF 是⊙O 的直径,则∠ BDF 的度数是________°.
三、解答题
13.⊙O的半径为5cm,弦AB=6cm,CD=8cm,且AB∥CD,求两弦之间的距离.
14.如图,A_B??????O??????_径,C是BA延长线上一点,点D在⊙O上,且CD=OB,CD的延长线交⊙O于点E.若∠C=19°,求∠BOE的度数.???
15.如图, 的半径 , 于点C, .求 的长.
四、综合题
16.如图, 中, ,P是斜边 上一个动点,以 为直径作 交 于点D,与 的另一个交点E,连接 .
(1)当 时,
①若 ,求 的度数;
②求证 ;
(2)当 , 时,是否存在点P,使得 是等腰三角形,若存在,求出所有符合条件的 的长.
17.如图,在 中,AB为直径,CD与 相切于点C,弦 于点E,连接AC.
(1)求证: ;
(2)当 时, , ,求AD的长.
18.如图,已知圆O是正_???è?????ABC_DEF外接圆,直径BE=8,点G、H分别在射线CD、EF上(点G不与点C、D重合),且∠GBH=60°,设CG=x , EH=y . 21·世纪*教育网
(1)如图①,当直线BG经过弧CD的中点Q时,求∠CBG的度数;
(2)如图②,当点G在边CD上时,试写出y关于x的函数关系式,
并写出x的取值范围;
(3)联结AH、EG , 如果△AFH与△DEG相似,求CG的长.
答案解析部分
一、单选题
1.【答案】 C
解:设直线MN的解析式为y=kx+b,
∴,
解得,
∴y=-x+,
当x=3时,y=-3≠5;当x=-3时,y=12;当x=13时,y=2≠-2;
∴点C在直线MN上,该三点不能构成圆.
故答案为:C.
2.【答案】 B
解:设弧AB的圆心为点O,过点O作OC⊥AB于点D,交弧AB于点C,
∴AD=AB=×300=150,
∵OC=OA=250
在Rt△AOD中
;
∴这些钢索中_???é??????????????_CD=OC-DO=250-200=50.
故答案为:B.
3.【答案】 B
解:如图,连接DC,
∵BD是⊙O的直径,
∴∠BCD=90°,
∴∠D=180-∠BCD-∠DBC=180°-90°-33°=57°,
又∵∠A=∠D,
∴∠A=57°.
故答案为:B.
4.【答案】 B
解: 切 于点 ,
故答案为:B.
5.【答案】 B
解:如图所示,连接BC、OD、OB,
∵∠A=40°,AB=AC,
∴∠ACB=70°,
∵BD∥AC,
∴∠ABD=∠A=40°,
∴∠ACD=∠ABD=40°,
∴∠BCD=30°,
则∠BOD=2∠BCD=60°,
又OD=OB,
∴△BOD是等边三角形,
则图中阴影部分的面积是S扇形BOD﹣S△BOD
= ﹣ ×22
= π﹣ ,
故答案为:B.
6.【答案】 A
解:连接OA、OB
∵O1A和O1B与⊙O2相切
∴∠O1AO2=∠O1BO2=90°
∴∠AO1B+∠AO2B=360°-(∠O1AO2+∠O1BO2)=180°
∴ 与 的弧长之和为
=
=
=
故答案为:A.
7.【答案】 C
解:整理变形的中心角为 =60°,
设正六边形的半径为r,
则其边长为r,
边长所对的弧长为: ,
∴正六边形的边长和边长所对的弧长的比为:r: =3: .
故答案为:C.
二、填空题
8.【答案】 2
解:因为直角三角形两条直角边长分别为6cm,8cm,所以该直角三角形的斜边长为10cm,
则这个三角形的内切圆的半径= =2(cm).
故答案为:2.
9.【答案】 2π
解:∵圆的半径为6,
∴面积为36π,
∵大量重复投掷后发现,小球落在阴影部分的概率稳定在 ,
∴扇形的面积为 =6π,
设扇形的弧长为l,则 l×3=6π,
解得:l=2π,
∴ 的长约为2π,
故答案为:2π.
10.【答案】 18°
解:连接OD,
∵CD=OA=OD,
∴∠C=∠DOC,
∴∠ODE=∠C+∠DOC=2∠C,
∵OD=OE,
∴∠E=∠EDO=2∠C,
∴∠EOB=∠C+∠E=3∠C=54°,
∴∠C=18°,
故答案为:18°.
11.【答案】
解:延长AO交圆于E点,
∵△ADB为等腰直角三角形,
∴AB:AD=,
∵OA=2,∴AE=4,
∵AE为直径,
∴∠ABE=90°,
∴∠ABE=∠ADC,
∵∠E和∠C所对的弧都为AB弧,
∴∠E=∠C,
∴AE:AC=AB:AD,
∴4:AC=,
∴AC=2.
故答案为: .
12.【答案】 54
解:连接AD,
∵AF是⊙O的直径,
∴∠ADF=90°,
∵五边形ABCDE是⊙O的内接正五边形,
∴∠ABC=∠C=108°,
∴∠ABD=72°,
∴∠F=∠ABD=72°,
∴∠FAD=18°,
∴∠CDF=∠DAF=18°,
∴∠BDF=36°+18°=54°,
故答案为:54.
三、解答题
13.【答案】 解:如图:过点O作OE⊥AB于E,交CD于F,
∵AB∥CD,
∴OF⊥CD,
∵OE过圆心,OE⊥AB,
∴EB= AB=3cm,
∵OB=5cm,
∴EO=4cm,
同理,OF=3cm,
∴EF=4-3=1cm,
当AB、CD位于圆心两旁时EF=4+3=7cm,
∴EF=1cm或EF=7cm.
14.【答案】 解:连接OD,
∵CD=OB=OD,∠C=19°,∴∠ODE=2∠C=38°,∵OD=OE,
∴∠E=∠EDO=38°,∴∠EOB=∠C+∠E=19°+38°=57°
15.【答案】 解:∵OC⊥AB,∠AOC=60°,
∴∠AOB=120°.
∵OA=2,
∴ 的长为:=.
四、综合题
16.【答案】 (1)解:①如图,连接PD,
∵PB为直径,
∴∠PDB=90°,
∠BPD=65°,
∴∠PBD=90°-∠BPD=25°,
∵ ,
∴ ,
∴,
∴∠C=∠BPE-∠PBD=65°-25°=40°;
②?证明:∵,
∴∠CBP=∠EBP,
∵∠ABE+∠A=∠C+∠A=90°,
∴∠C=∠ABE,
∴∠ABP=∠ABE+∠EBP,∠APB=∠C+∠CBP,
∴∠ABP=∠APB,
∴AP=AB;
(2)解:存在,
如图,连接PD,
由AB=15,BC= 20,
由勾股定理得: AC===25,
∵AB.BC=AC.BE ,
即×15×20=×25×BE,
∴ BE=12,
∵BP是直径,
∴∠PDB =90° ,
∵∠ABC =90° ,
∴PD∥AB ,
∴△DCP∽△BCA ,
∴,
∴,
△BDE是等腰角形,分三种情况:
当BD= BE时,BD=BE=12,
∴CD=BC-BD=20-12=8,
∴ CP=CD=x8=10,
当BD= ED时,可知点D是Rt△CBE斜边的中线,
∴CD=BC=10,
∴CP=CD=×10=,
当DE=BE时,作EH⊥BC, 则H是BD中点,EH//AB, 如图,
AE===9,
:.CE=AC-AE=25-9=16, CH=BC-BH=20-BH ,
∵EH∥AB,
∴,
即,
解得: BH=,
∴BD=2BH=,
∴CD= BC-BD=20-=,
∴CP=CD=,
综上所述,△BDE 是等腰三角形,符合条件的CP的长为10或或7.
17.【答案】 (1)证明:连接OC,
∵CD切??于点C,
∴∠OCD=90°,
∴∠ACD+∠ACO=90°.
∵CF⊥AB,
∴∠AEC=90°,
∴∠ACF+∠CAE=90°.
∵OA=OC,
∴∠ACO=∠CAE,
∴∠ACD=∠ACF.
(2)解:由(1)可知,∠ACD=∠ACF.
∵CF⊥AB,CF=12,
∴CE=CF=6.
设?的半径为r,则OE=r-3.
在Rt△OEC中,OC2=OE2+CE2 , 即r2=(r-3)2+62 ,
解得r=,
∴AE=AB-BE=15-3=12.
∵∠ACD=∠ACF,AD⊥CD,CF⊥AB,
∴AD=AE=12(cm).
18.【答案】 (1)解:如图①,联结OQ.
∵正六边形ABCDEF,∴BC=DE,∠ABC=120°.
∴ ,∠EBC= ∠ABC=60°.
∵点Q是 的中点, ∴ ∴ , 即 . ∴∠BOQ=∠EOQ, 又∵∠BOQ+∠EOQ=180°,
∴∠BOQ=∠EOQ=90°.
又∵BO=OQ,∴∠OBQ=∠BQO=45°, ∴∠CBG=60° 45°=15°.
(2)解:如图②,在BE上截取EM=HE,联结HM.
∵正六边形ABCDEF,直径BE=8, ∴BO=OE=BC=4,∠C=∠FED=120°,
∴∠FEB= ∠FED=60°.
∵EM=HE,EH=y,
∴EM=HE=HM=y,∠HME=60°,
∴∠C=∠HMB=120°.
∵∠EBC=∠GBH=60°, ∴∠EBC ∠GBE=∠EBC ∠GBE, 即∠HBE=∠GBC. ∴△BCG∽△BMH,∴ .
又∵CG= x,BE=8,BC=4,∴ ,
∴y与x的函数关系式为 ( )
(3)解:如图③,当点G在边CD上时.
由于△AFH∽△EDG,且∠CDE=∠AFE=120°, ① 当 .∵AF=ED,∴FH=DG, 即: ,解分式方程得 . 经检验 是原方程的解,但不符合题意舍去. ② 当 .即: ,解分式方程得 . 经检验 是原方程的解,但不符合题意舍去. 2-1-c-n-j-y
如图④,当点G在CD的延长线上时.
由于△AFH∽△EDG,且∠EDG=∠AFH=60°,
① 当 .∵AF=ED,∴FH=DG, 即: ,解分式方程得 . 经检验 是原方程的解,但不符合题意舍去. ② 当 .即: ,解分式方程得 . 经检验 是原方程的解,且符合题意. 21cnjy.com
∴综上所述,如果△AFH与△DEG相似,那么CG的长为12.
_21?????????è?????(www.21cnjy.com)_
