粤教版(2019)物理必修第二册 第一章 抛体运动 本章小结课件(38张ppt)
文档属性
| 名称 | 粤教版(2019)物理必修第二册 第一章 抛体运动 本章小结课件(38张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-12 00:00:00 | ||
图片预览











文档简介
第一章 抛体运动
本章小结
构建知识网络
归纳专题小结
1.确定方向:确定两个分运动方向上的初速度大小和方向,以及在这两个方向上的物体所受力的大小和方向(即分运动方向上的加速度大小和方向).
2.应用平行四边形法则:将两个分运动的速度和分运动方向的力进行矢量合成,求出合速度和合力(或合加速度)的大小和方向.
专题
互成角度的两个直线运动的合运动的性质和轨迹的判断
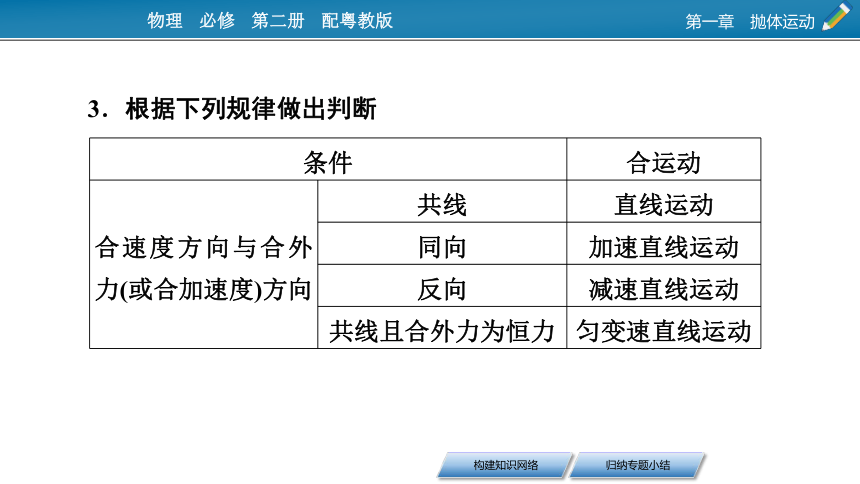
3.根据下列规律做出判断
条件
合运动
合速度方向与合外力(或合加速度)方向
共线
直线运动
同向
加速直线运动
反向
减速直线运动
共线且合外力为恒力
匀变速直线运动
条件
合运动
合速度方向与合外力(或合加速度)方向
不共线
曲线运动
成锐角
加速曲线运动
成钝角
减速曲线运动
成直角
匀速率曲线运动
不共线且合外力为恒力
匀变速曲线运动
例1 海浪中行驶的摩托艇在某段时间内沿水平方向和竖直方向的位移分别为x=-2t2-6t,y=0.05t2+4t(t的单位是s,x、y的单位是m),则关于摩托艇在该段时间内的运动,下列说法正确的是 ( )
A.摩托艇在水平方向的分运动是匀减速直线运动
B.t=0时摩托艇的速度为零
C.摩托艇的运动是匀变速曲线运动
D.摩托艇运动的加速度大小为4 m/s2
专题
运动的合成与分解的两种典型模型
2.绳(或杆)端的速度分解模型
当绳连接的两个物体的运动方向与绳不共线时,如图所示,绳末端的运动可以看成两个分运动的合成,一是沿绳方向被带动,绳长缩短,使绳缩短的速度为v0;二是垂直于绳、以定滑轮为圆心的转动,它不改变绳长,即合速度vA分解为沿绳的速度v0与垂直绳的速度v1.
不可伸长的绳或杆,沿绳或杆上的速度大小是相同的,这是解决问题的关键.
例3 如图所示,一根长直轻杆AB在墙角沿竖直墙和水平地面滑动,当AB杆和墙的夹角为θ时,杆的A端沿墙下滑的速度大小为v1,B端沿地面滑动的速度大小为v2,则v1、v2的关系是 ( )
A.v1=v2
B.v1=v2cos θ
C.v1=v2tan θ
D.v1=v2sin θ
解析:A、B两点速度分解如图所示,由沿杆方向的速度相等,得v1cos θ=v2sin θ,所以v1=v2tan θ,故C正确.
答案:C
平抛运动是典型的匀变速曲线运动,它的动力学特征是水平方向有初速度而不受外力,竖直方向只受重力而无初速度,抓住了平抛运动这个初始条件,也就抓住了解题关键.现将常见的几种解题方法介绍如下:
1.利用平抛运动的时间特点解题
平抛运动可分解成水平方向的匀速直线运动和竖直方向的自由落体运动,只要抛出的时间相同,下落的高度和竖直分速度就相同.
专题
利用平抛运动的特征来解题的方法
2.利用平抛运动的偏转角解题
设平抛运动的物体,下落高度为h,水平位移为x,速度vA与初速度v0的夹角为θ.如图所示.
3.利用平抛运动的轨迹解题
平抛运动的轨迹是一条抛物线,已知抛物线上的任一段,就可以求出水平初速度和抛出点,其他物理量也就迎刃而解了.如图所示为小球做平抛运动的某段轨迹,在轨迹上任取两点A和B,
例4 如图所示,滑雪运动员经过一段加速滑行后从A点以水平速度v0飞出,落到斜坡上的B点,已知AB两点距离s=75 m,斜坡与水平面的夹角α=37°,不计空气阻力(sin 37°=0.6,cos 37°=0.8,g取10 m/s2).求:
(1)运动员在空中飞行的时间.
(2)运动员在A点水平速度v0的大小.
例5 在离地某一高度的同一位置,有A、B两个小球,A球以vA=3 m/s的速度水平向左抛出,同时B球以vB=4 m/s的速度水平向右抛出,试求出两个小球的速度方向垂直时,它们之间的距离为多大?
解析:如图所示,由于两个小球是以
同一高度、同一时刻抛出,它们始终在
同一水平位置上,且有v′Ay=v′By=gt.
典练素养提升
1.一质点受两个互成锐角的恒力F1和F2作用,由静止开始做匀加速直线运动,若运动过程中保持二力方向不变,但F1突然增大到F1+ΔF,则质点以后 ( )
A.继续做匀变速直线运动
B.在相等时间内速度的变化量一定相等
C.可能做匀速直线运动
D.可能做变加速曲线运动
【答案】B
2.跳伞表演是人们普遍喜欢的观赏性体育项目.如图所示,当运动员从直升机由静止跳下后,在下落过程中会受到水平风力的影响,下列说法正确的是 ( )
A.风力越大,运动员下落时间越长,运动员可完成更多的动作
B.风力越大,运动员着地速度越大,有可能对运动员造成伤害
C.运动员下落时间与风力有关
D.运动员着地速度与风力无关
【答案】B
【解析】运动员同时参与了两个分运动:竖直方向下落运动和水平方向随风飘动,两个分运动同时发生,相互独立.因此,水平风速越大,落地的合速度越大,但落地时间不变.
3. (多选)如图所示,在河水速度恒定的小河中,一小船保持船头始终垂直河岸,从一侧岸边向对岸行驶,小船的轨迹是一个弯曲的“S”形,则 ( )
A.小船垂直河岸的速度大小恒定不变
B.小船垂直河岸的速度大小先增大后减小
C.与小船以出发时的速度匀速渡河相比,渡河时间变长了
D.与小船以出发时的速度匀速渡河相比,渡河时间变短了
【答案】BD
【解析】小船在沿河岸的方向上随河水做匀速直线运动,即在相同的时间间隔内,沿河岸方向上的位移是相同的;在垂直河岸的方向上,在相等的时间间隔内(参照小船沿河岸方向上的位移),位移的变化量先逐渐增大再逐渐减小,所以速度先增大后减小;因中间那段时间垂直河岸方向的速度较大,所以与小船以出发时的速度匀速渡河相比,渡河时间变短了,B、D正确.
5.(多选)如图所示,从倾角为θ的足够长的斜面顶端,先后将同一小球以不同的初速度水平向右抛出.第一次初速度为v1,球落到斜面上前一瞬间的速度方向与斜面夹角为α1,落点与抛出点间的距离为s1.第二次初速度为v2,且v2=3v1,球落到斜面上前一瞬间的速度方向与斜面夹角为α2,落点与抛出点间的距离为s2,则是 ( )
A.α1=α2
B.α2≠α1
C.s2=3s1
D.s2=9s1
【答案】AD
6.跳台滑雪是勇敢者的运动,运动员在专用滑雪板上,不带雪杖在助滑路上获得高速后水平飞出,在空中飞行一段距离后着陆,这项运动极为壮观.设一位运动员由a点沿水平方向跃起,到山坡b点着陆,如图所示.测得a、b间距离L=40 m,山坡倾角θ=30°,山坡可以看成一个斜面.不计空气阻力,g取10 m/s2,试计算:
(1)运动员起跳后在空中从a到b飞行的时间.
(2)运动员在a点的水平速度大小.
本章小结
构建知识网络
归纳专题小结
1.确定方向:确定两个分运动方向上的初速度大小和方向,以及在这两个方向上的物体所受力的大小和方向(即分运动方向上的加速度大小和方向).
2.应用平行四边形法则:将两个分运动的速度和分运动方向的力进行矢量合成,求出合速度和合力(或合加速度)的大小和方向.
专题
互成角度的两个直线运动的合运动的性质和轨迹的判断
3.根据下列规律做出判断
条件
合运动
合速度方向与合外力(或合加速度)方向
共线
直线运动
同向
加速直线运动
反向
减速直线运动
共线且合外力为恒力
匀变速直线运动
条件
合运动
合速度方向与合外力(或合加速度)方向
不共线
曲线运动
成锐角
加速曲线运动
成钝角
减速曲线运动
成直角
匀速率曲线运动
不共线且合外力为恒力
匀变速曲线运动
例1 海浪中行驶的摩托艇在某段时间内沿水平方向和竖直方向的位移分别为x=-2t2-6t,y=0.05t2+4t(t的单位是s,x、y的单位是m),则关于摩托艇在该段时间内的运动,下列说法正确的是 ( )
A.摩托艇在水平方向的分运动是匀减速直线运动
B.t=0时摩托艇的速度为零
C.摩托艇的运动是匀变速曲线运动
D.摩托艇运动的加速度大小为4 m/s2
专题
运动的合成与分解的两种典型模型
2.绳(或杆)端的速度分解模型
当绳连接的两个物体的运动方向与绳不共线时,如图所示,绳末端的运动可以看成两个分运动的合成,一是沿绳方向被带动,绳长缩短,使绳缩短的速度为v0;二是垂直于绳、以定滑轮为圆心的转动,它不改变绳长,即合速度vA分解为沿绳的速度v0与垂直绳的速度v1.
不可伸长的绳或杆,沿绳或杆上的速度大小是相同的,这是解决问题的关键.
例3 如图所示,一根长直轻杆AB在墙角沿竖直墙和水平地面滑动,当AB杆和墙的夹角为θ时,杆的A端沿墙下滑的速度大小为v1,B端沿地面滑动的速度大小为v2,则v1、v2的关系是 ( )
A.v1=v2
B.v1=v2cos θ
C.v1=v2tan θ
D.v1=v2sin θ
解析:A、B两点速度分解如图所示,由沿杆方向的速度相等,得v1cos θ=v2sin θ,所以v1=v2tan θ,故C正确.
答案:C
平抛运动是典型的匀变速曲线运动,它的动力学特征是水平方向有初速度而不受外力,竖直方向只受重力而无初速度,抓住了平抛运动这个初始条件,也就抓住了解题关键.现将常见的几种解题方法介绍如下:
1.利用平抛运动的时间特点解题
平抛运动可分解成水平方向的匀速直线运动和竖直方向的自由落体运动,只要抛出的时间相同,下落的高度和竖直分速度就相同.
专题
利用平抛运动的特征来解题的方法
2.利用平抛运动的偏转角解题
设平抛运动的物体,下落高度为h,水平位移为x,速度vA与初速度v0的夹角为θ.如图所示.
3.利用平抛运动的轨迹解题
平抛运动的轨迹是一条抛物线,已知抛物线上的任一段,就可以求出水平初速度和抛出点,其他物理量也就迎刃而解了.如图所示为小球做平抛运动的某段轨迹,在轨迹上任取两点A和B,
例4 如图所示,滑雪运动员经过一段加速滑行后从A点以水平速度v0飞出,落到斜坡上的B点,已知AB两点距离s=75 m,斜坡与水平面的夹角α=37°,不计空气阻力(sin 37°=0.6,cos 37°=0.8,g取10 m/s2).求:
(1)运动员在空中飞行的时间.
(2)运动员在A点水平速度v0的大小.
例5 在离地某一高度的同一位置,有A、B两个小球,A球以vA=3 m/s的速度水平向左抛出,同时B球以vB=4 m/s的速度水平向右抛出,试求出两个小球的速度方向垂直时,它们之间的距离为多大?
解析:如图所示,由于两个小球是以
同一高度、同一时刻抛出,它们始终在
同一水平位置上,且有v′Ay=v′By=gt.
典练素养提升
1.一质点受两个互成锐角的恒力F1和F2作用,由静止开始做匀加速直线运动,若运动过程中保持二力方向不变,但F1突然增大到F1+ΔF,则质点以后 ( )
A.继续做匀变速直线运动
B.在相等时间内速度的变化量一定相等
C.可能做匀速直线运动
D.可能做变加速曲线运动
【答案】B
2.跳伞表演是人们普遍喜欢的观赏性体育项目.如图所示,当运动员从直升机由静止跳下后,在下落过程中会受到水平风力的影响,下列说法正确的是 ( )
A.风力越大,运动员下落时间越长,运动员可完成更多的动作
B.风力越大,运动员着地速度越大,有可能对运动员造成伤害
C.运动员下落时间与风力有关
D.运动员着地速度与风力无关
【答案】B
【解析】运动员同时参与了两个分运动:竖直方向下落运动和水平方向随风飘动,两个分运动同时发生,相互独立.因此,水平风速越大,落地的合速度越大,但落地时间不变.
3. (多选)如图所示,在河水速度恒定的小河中,一小船保持船头始终垂直河岸,从一侧岸边向对岸行驶,小船的轨迹是一个弯曲的“S”形,则 ( )
A.小船垂直河岸的速度大小恒定不变
B.小船垂直河岸的速度大小先增大后减小
C.与小船以出发时的速度匀速渡河相比,渡河时间变长了
D.与小船以出发时的速度匀速渡河相比,渡河时间变短了
【答案】BD
【解析】小船在沿河岸的方向上随河水做匀速直线运动,即在相同的时间间隔内,沿河岸方向上的位移是相同的;在垂直河岸的方向上,在相等的时间间隔内(参照小船沿河岸方向上的位移),位移的变化量先逐渐增大再逐渐减小,所以速度先增大后减小;因中间那段时间垂直河岸方向的速度较大,所以与小船以出发时的速度匀速渡河相比,渡河时间变短了,B、D正确.
5.(多选)如图所示,从倾角为θ的足够长的斜面顶端,先后将同一小球以不同的初速度水平向右抛出.第一次初速度为v1,球落到斜面上前一瞬间的速度方向与斜面夹角为α1,落点与抛出点间的距离为s1.第二次初速度为v2,且v2=3v1,球落到斜面上前一瞬间的速度方向与斜面夹角为α2,落点与抛出点间的距离为s2,则是 ( )
A.α1=α2
B.α2≠α1
C.s2=3s1
D.s2=9s1
【答案】AD
6.跳台滑雪是勇敢者的运动,运动员在专用滑雪板上,不带雪杖在助滑路上获得高速后水平飞出,在空中飞行一段距离后着陆,这项运动极为壮观.设一位运动员由a点沿水平方向跃起,到山坡b点着陆,如图所示.测得a、b间距离L=40 m,山坡倾角θ=30°,山坡可以看成一个斜面.不计空气阻力,g取10 m/s2,试计算:
(1)运动员起跳后在空中从a到b飞行的时间.
(2)运动员在a点的水平速度大小.
同课章节目录
- 第一章 抛体运动
- 第一节 曲线运动
- 第二节 运动的合成与分解
- 第三节 平抛运动
- 第四节 生活和生产中的抛体运动
- 第二章 圆周运动
- 第一节 匀速圆周运动
- 第二节 向心力与向心加速度
- 第三节 生活中的圆周运动
- 第四节 离心现象及其应用
- 第三章 万有引力定律
- 第一节 认识天体运动
- 第二节 认识万有引力定律
- 第三节 万有引力定律的应用
- 第四节 宇宙速度与航天
- 第四章 机械能及其守恒定律
- 第一节 功
- 第二节 功率
- 第三节 动能 动能定理
- 第四节 势能
- 第五节 机械能守恒定律
- 第六节 验证机械能守恒定律
- 第七节 生产和生活中的机械能守恒
- 第五章 牛顿力学的局限性与相对论初步
- 第一节 牛顿力学的成就与局限性
- 第二节 相对论时空观
- 第三节 宇宙起源和演化
