2.4三角形的中位线 同步练习(含解析)
图片预览



文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学湘教版八年级下册2.4三角形的中位线
同步练习
一、单选题
1.如图,D、E分别是△ABC的边AB、AC的中点,若BC=6,则DE=(?
)
A.?2???????????????????????????????????????????B.?3???????????????????????????????????????????C.?4???????????????????????????????????????????D.?5
2.如图,在
中,点
,
,
分别是边
,
,
的中点,若
,则四边形
的周长为(??
)
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?4???????????????????????????????????????????D.?8
3.如图,要测量池塘两侧的两点A、B之间的距离,可以取一个能直接到达A、B的点C,连结CA、CB,分别在线段CA、CB上取中点D、E,连结DE,测得DE=35m,则可得A、B之间的距离为(??
)
A.?30m???????????????????????????????????B.?70m???????????????????????????????????C.?105m???????????????????????????????????D.?140m
4.如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20,那么△DEF的周长是(
??)
A.?20?????????????????????????????????????????B.?15?????????????????????????????????????????C.?10?????????????????????????????????????????D.?5
5.如图所示,?ABCD的对角线AC,BD相交于点O,点E是CD的中点,若BC=6,则OE的长为(?
)
A.?2??????????????????????????????????????????B.?2.5??????????????????????????????????????????C.?3??????????????????????????????????????????D.?4
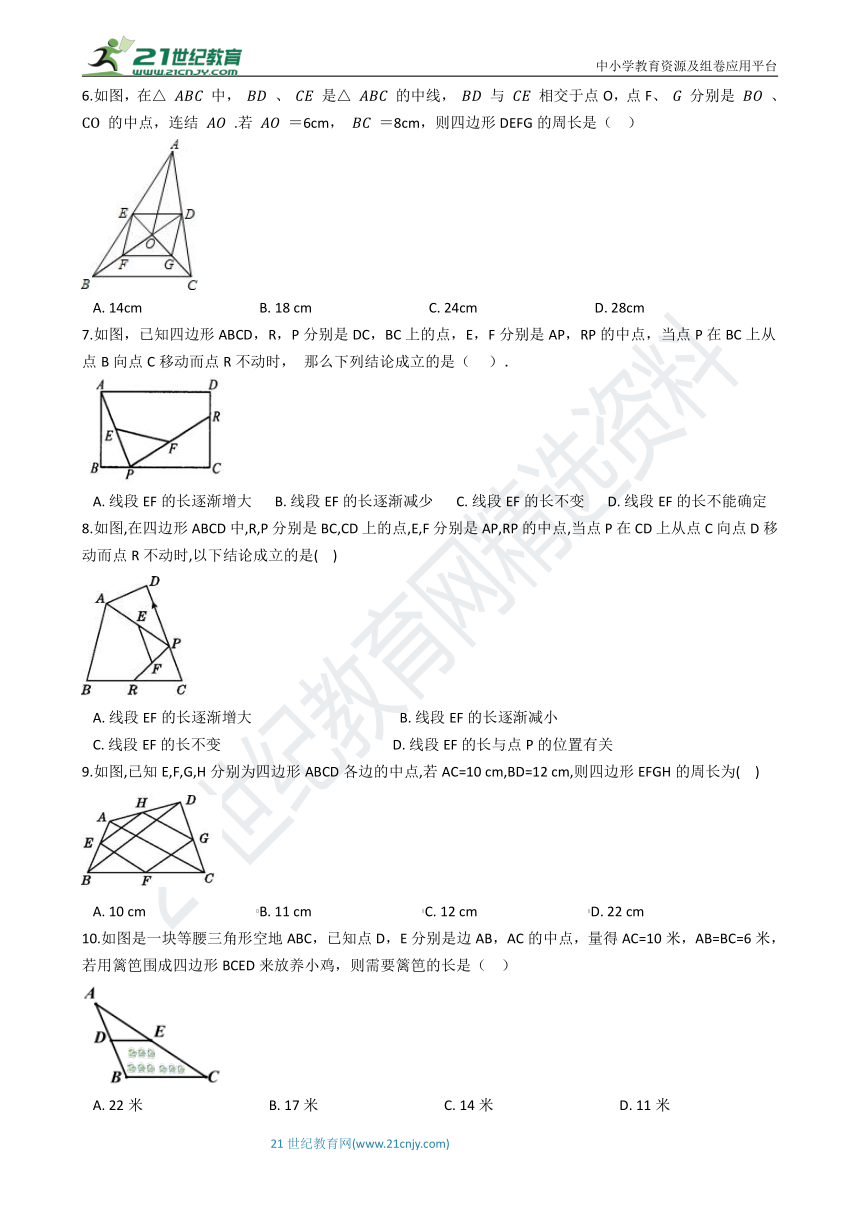
6.如图,在△
中,
、
是△
的中线,
与
相交于点O,点F、
分别是
、
的中点,连结
.若
=6cm,
=8cm,则四边形DEFG的周长是(??
)
A.?14cm??????????????????????????????????B.?18
cm??????????????????????????????????C.?24cm??????????????????????????????????D.?28cm
7.如图,已知四边形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动而点R不动时,
那么下列结论成立的是(???
).
A.?线段EF的长逐渐增大??????B.?线段EF的长逐渐减少??????C.?线段EF的长不变??????D.?线段EF的长不能确定
8.如图,在四边形ABCD中,R,P分别是BC,CD上的点,E,F分别是AP,RP的中点,当点P在CD上从点C向点D移动而点R不动时,以下结论成立的是(??
)
A.?线段EF的长逐渐增大???????????????????????????????????????????B.?线段EF的长逐渐减小
C.?线段EF的长不变??????????????????????????????????????????????????D.?线段EF的长与点P的位置有关
9.如图,已知E,F,G,H分别为四边形ABCD各边的中点,若AC=10
cm,BD=12
cm,则四边形EFGH的周长为(??
)
A.?10
cm????????????????????????????????B.?11
cm????????????????????????????????C.?12
cm????????????????????????????????D.?22
cm
10.如图是一块等腰三角形空地ABC,已知点D,E分别是边AB,AC的中点,量得AC=10米,AB=BC=6米,若用篱笆围成四边形BCED来放养小鸡,则需要篱笆的长是(
??)
A.?22米????????????????????????????????????B.?17米????????????????????????????????????C.?14米????????????????????????????????????D.?11米
二、填空题
11.如图,在
中,
分别是
的中点,连接
,若
,则四边形
的周长是________.
12.已知三角形的周长为20cm,连接各边中点所得的三角形的周长为________cm.
13.如图,已知△ABC的周长为a,A1B1
,
B1C1
,
A1C1是△ABC的三条中位线,它们构成了△A1B1C1
,
△A2B2C2是由△A1B1C1的三条中位线A2B2
,
B2C2
,
A2C2构成的……如此进行下去,得到△AnBnCn
,
则△A1B1C1的周长为________,△A2B2C2的周长为________,△A3B3C3的周长为________,△AnBnCn的周长为________.
14.如图所示,在四边形ABCD中,AB=CD=4,M、N、P分别是AD、BC、BD的中点,∠ABD=20°,∠BDC=80°,则MN的长是________.
三、解答题
15.请叙述三角形中位线定理并证明.
16.如图,在△ABC中,已知AB=6,AC=10,AD平分∠BAC,BD⊥AD于点D,E为BC中点.求DE的长.
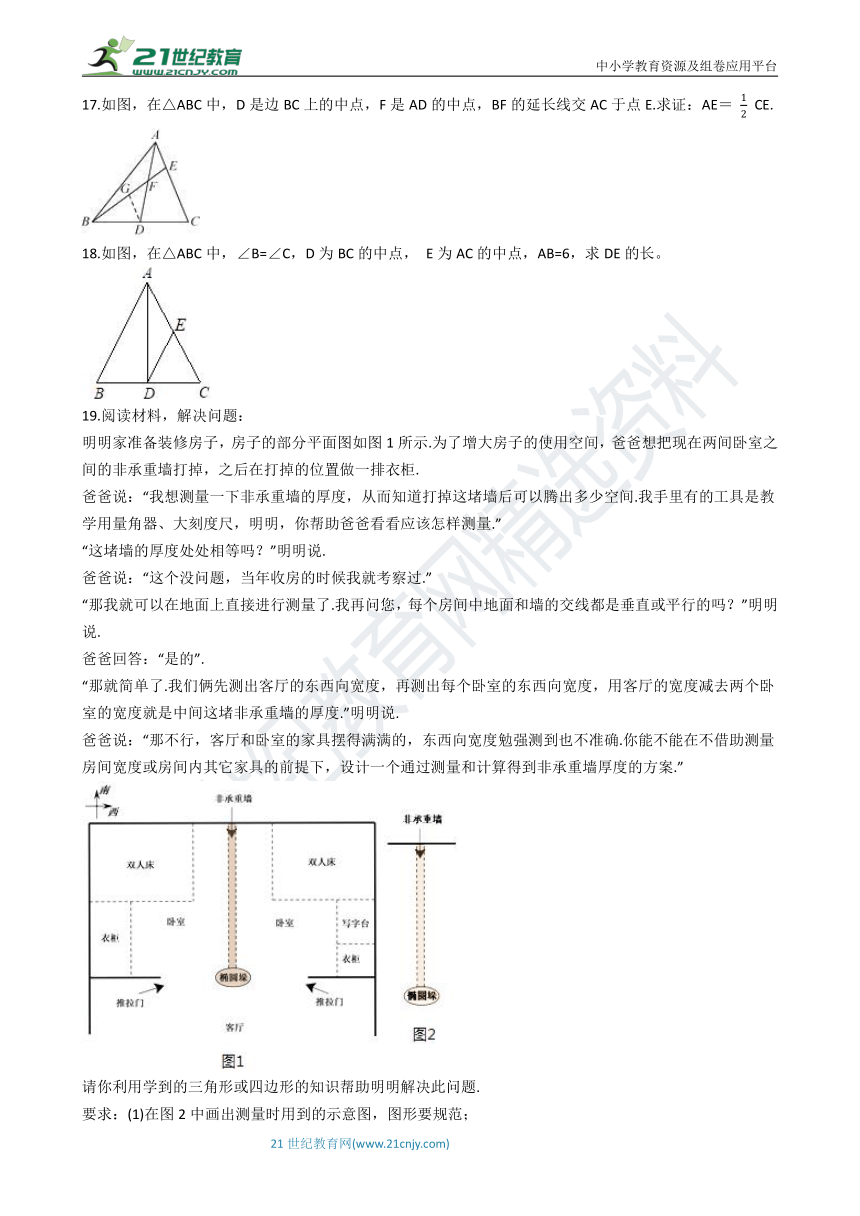
17.如图,在△ABC中,D是边BC上的中点,F是AD的中点,BF的延长线交AC于点E.求证:AE=
CE.
18.如图,在△ABC中,∠B=∠C,D为BC的中点,
E为AC的中点,AB=6,求DE的长。
19.阅读材料,解决问题:
明明家准备装修房子,房子的部分平面图如图1所示.为了增大房子的使用空间,爸爸想把现在两间卧室之间的非承重墙打掉,之后在打掉的位置做一排衣柜.
爸爸说:“我想测量一下非承重墙的厚度,从而知道打掉这堵墙后可以腾出多少空间.我手里有的工具是教学用量角器、大刻度尺,明明,你帮助爸爸看看应该怎样测量.”
“这堵墙的厚度处处相等吗?”明明说.
爸爸说:“这个没问题,当年收房的时候我就考察过.”
“那我就可以在地面上直接进行测量了.我再问您,每个房间中地面和墙的交线都是垂直或平行的吗?”明明说.
爸爸回答:“是的”.
“那就简单了.我们俩先测出客厅的东西向宽度,再测出每个卧室的东西向宽度,用客厅的宽度减去两个卧室的宽度就是中间这堵非承重墙的厚度.”明明说.
爸爸说:“那不行,客厅和卧室的家具摆得满满的,东西向宽度勉强测到也不准确.你能不能在不借助测量房间宽度或房间内其它家具的前提下,设计一个通过测量和计算得到非承重墙厚度的方案.”
请你利用学到的三角形或四边形的知识帮助明明解决此问题.
要求:(1)在图2中画出测量时用到的示意图,图形要规范;
(2)简要叙述测量过程;
(3)写出测量的依据.
答案解析部分
一、单选题
1.【答案】
B
【解析】【解答】解:∵D、E分别是△ABC的边AB、AC的中点,
∴DE是△ABC的中位线,
∴DE=
BC=3,
故答案为:B.
【分析】由已知可得DE是△ABC的中位线,再根据三角形的中位线等于第三边的一半,可求出DE的长。
2.【答案】
C
【解析】【解答】解:∵点D,E,F分别是边AB,BC,AC的中点,
∴AD=
AB=1,AF=
AC=1,DE、FE是△ABC的中位线,
∴DE=
AC=1,EF=
AB=1,
∴四边形ADEF的周长=AD+DE+EF+AF=4,
故答案为:C.
【分析】根据三角形中位线定理、线段中点的概念计算,得到答案.
3.【答案】
B
【解析】【解答】解:∵D、E分别是AC、BC的中点,
∴DE是△ABC的中位线,
根据三角形的中位线定理,得:AB=2DE=70m.
故答案为:B.
【分析】由D,E分别是边AC,AB的中点,首先判定DE是三角形的中位线,然后根据三角形的中位线定理求得AB的长即可.
4.【答案】
C
【解析】【解答】∵D、E分别是△ABC的边BC、AB的中点,
∴DE=
AC,同理
EF=
BC,DF=
AB,∴C△DEF=DE+EF+DF=
(AC+BC+AB)=
×20=10.
故答案为:C.
【分析】利用三角形的中位线定理得到线段的等量关系,再求出三角形的周长即可.
5.【答案】
C
【解析】【解答】解:∵?ABCD的对角线AC、BD相交于点O,
∴OB=OD,
∵点E是CD的中点,
∴CE=DE,
∴OE是△BCD的中位线,
∵BC=6,
∴OE=
BC=3.
故答案为:C.
【分析】先说明OE是△BCD的中位线,再根据三角形的中位线平行于第三边并且等于第三边的一半求解.
6.【答案】
A
【解析】【解答】解:∵点F、G分别是BO、CO的中点,BC
=
8cm
∴FG=
BC=4
cm
∵BD、CE是△ABC的中线
∴DE=
BC=4
cm
∵点F、G、E、D分别是BO、CO、AB、AC的中点,AO
=
6cm
∴EF=
AO=3
cm,DG=
AO=3
cm
∴四边形DEFG的周长=EF+FG+DG+DE=14?cm
故答案为:A
【分析】根据三角形的中位线定理得出FG=
BC=4
cm,DE=
BC=4
cm,点F、G、E、D分别是BO、CO、AB、AC的中点,AO
=
6cm,得出EF=
AO=3
cm,DG=
AO=3
cm,进而求出
四边形DEFG的周长
。
7.【答案】
C
【解析】【解答】解:如图,连接AR,
∵E、F分别是AP、RP的中点,
∴EF为△APR的中位线,
∴EF=
AR,为定值.
∴线段EF的长不改变.
故答案为:C.
【分析】因为R不动,所以AR不变.根据三角形中位线定理可得EF=
AR,因此线段EF的长不变.
8.【答案】
C
【解析】【解答】解:如图,连接AR,
∵E,F分别是AP,RP的中点
∴EF是△PAR的中位线,
∴EF=AR
∵当点P在CD上从点C向点D移动而点R不动,
∴线段EF的长不变,
故答案为:C
【分析】根据已知条件E,F分别是AP,RP的中点,因此连接AR,构造三角形的中位线,得出EF=AR,由于点R不动,因此AR是一个定值,即可得出答案。
9.【答案】
D
【解析】【解答】解:∵E、F分别是AB、BC的中点,
∴EF=AC=×10=5
同理可得:HG=AC=×10=5
EH=BD=×12=6
FG=BD=×12=6
∴四边形EFGH的周长=EF+HG+EH+FG=5+5+6+6=22
故答案为:D
【分析】根据三角形的中位线定理及已知条件分别求出EF、HG、EH、FG的长,再求出四边形EFGH的周长即可。
10.【答案】
B
【解析】【解答】由题意可知,点D,E分别是边AB,AC的中点,
?
?
?
,即
四边形BCED的周长
故答案为:B
【分析】利用三角形中位线定理求出DE的长,再利用线段中点的定义求出BD、CE的长,然后求出四边形BCDE的周长。
二、填空题
11.【答案】
22cm
【解析】【解答】解:∵
分别是
的中点,
,
∴
,
,
,
,
∴四边形
的周长为
,
故答案为:
.
【分析】通过线段中点和三角形的中位线可求出各边的长,然后即可求出四边形
的周长.
12.【答案】
10
【解析】【解答】解:如图,
∵
分别为
的中点,
∴
,
∵
,
∴
,
故答案为:10.
【分析】根据中位线定理分别求出DE、EF和DF各边的长,则△DEF的周长可求.
13.【答案】
;;;a2n
【解析】【解答】解:∵A1B1
,
B1C1
,
A1C1是△ABC的三条中位线,
∴A1B1=AB,A1C1=AC,C1B1=CB,
∴△A1B1C1的周长=(AB+AC+CB)=a.
同理:A2B2C2的周长为a,△A3B3C3的周长为a,△AnBnCn的周长为.
【分析】根据中位线定理可知,△A1B1C1的周长为
,△A2B2C2的周长为
·
=
……△AnBnCn的周长为
.
14.【答案】
2
【解析】【解答】解:作PH⊥MN于H,
∵M、N、P分别是AD、BC、BD的中点,
∴PM=
AB=2,PN=
CD=2,PM∥AB,PN∥CD,
∴∠MPD=∠ABD=20°,∠BPN=∠BDC=80°,PM=PN,
∴∠MPN=120°,
∵PM=PN,
∴∠PMN=30°,MH=HN,
∴PH=
PM=1,
由勾股定理得,MH=
=
,
∴MN=2MH=2
,
故答案为:2
.
【分析】作PH⊥MN于H,根据三角形中位线定理求出PM、PN、∠MPN,根据等腰三角形的性质、勾股定理计算即可.
三、解答题
15.【答案】
解:已知:△ABC中,点E、F分别是AB、AC的中点,
求证:三角形的中位线平行于第三边并且等于第三边的一半,
证明:如图,延长EF到D,使FD=EF,
∵点F是AC的中点,
∴AF=CF,
在△AEF和△CDF中,
,
∴△AEF≌△CDF(SAS),
∴AE=CD,∠D=∠AEF,
∴AB∥CD,
∵点E是AB的中点,
∴AE=BE,
∴BE=CD,
∴BE∥CD,BE=CD
∴四边形BCDE是平行四边形,
∴DE∥BC,DE=BC,
∴DE∥BC且DE=
BC.
【解析】【分析】作出图形,然后写出已知、求证,延长EF到D,使FD=EF,利用“边角边”证明△AEF和△CDF全等,根据全等三角形对应边相等可得AE=CD,全等三角形对应角相等可得∠D=∠AEF,再求出CE=CD,根据内错角相等,两直线平行判断出AB∥CD,然后判断出四边形BCDE是平行四边形,根据平行四边形的性质可得DE∥BC,DE=BC.
16.【答案】
解:延长BD交AC于点F.∵∠BAD=∠FAD,AD=AD,∠ADB=∠ADF=90°.∴△ABD≌△AFD,∴AB=AF=6,BD=DF.又∵E为BC中点,∴DE=
FC=
(AC-AF)=
(10-6)=2
【解析】【分析】延长BD交AC于点F.由已知条件可用角边角证得△ABD≌△AFD,所以AB=AF=6,BD=DF.而E为BC中点,所以DE是三角形BCF的中位线,根据三角形的中位线定理可得DE=?FC=?(AC-AF)=?(10-6)=2。
17.【答案】
解:取BE的中点G,连结DG.∵D,G分别是BC,BE的中点,∴DG是△BCE的中位线,∴DG∥AC,DG=
CE.∴∠FAE=∠FDG,∠AEF=∠DGF.∵F是AD的中点,∴AF=DF.∴△AEF≌△DGF(AAS).∴AE=DG.∴AE=
CE
【解析】【分析】取BE的中点G,连结DG.因为D是边BC上的中点,所以根据三角形的中位线定理可得DG∥AC,DG=?
CE,由平行线的性质可得∠FAE=∠FDG,∠AEF=∠DGF,因为F是AD的中点,所以AF=DF.用角角边可证△AEF≌△DGF,所以AE=DG.即AE=?CE。
18.【答案】
解:∵D为BC的中点,E为AC的中点,
∴DE为△ABC的中位线,
∴DE=
AB=12×6=3.
【解析】【分析】根据三角形的中位线定理直接求出得到DE=AB.
19.【答案】
如图,在椭圆垛的两边测出AC=BD,过点C、D作出CE⊥AC、DF⊥BD,可知E、C、D、F在一条直线上,同时测出EC、DF的长,在客厅内找一点P,连接PE、PF,通过测量找得PE、PF的中点M、N,测出MN的长,根据三角形的中位线定理即可得EF的长,用EF的长减去EC、DF的长即可得CD的长.
【解析】【分析】根据非承重墙的一端存在椭圆垛,需要三角形或四边形,测出AC=BD,再得出EC、DF的长,根据中位线定理得出EF的长度,最后得出CD的长.
(
第
一
页
共
1
页
)
21世纪教育网(www.21cnjy.com)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学湘教版八年级下册2.4三角形的中位线
同步练习
一、单选题
1.如图,D、E分别是△ABC的边AB、AC的中点,若BC=6,则DE=(?
)
A.?2???????????????????????????????????????????B.?3???????????????????????????????????????????C.?4???????????????????????????????????????????D.?5
2.如图,在
中,点
,
,
分别是边
,
,
的中点,若
,则四边形
的周长为(??
)
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?4???????????????????????????????????????????D.?8
3.如图,要测量池塘两侧的两点A、B之间的距离,可以取一个能直接到达A、B的点C,连结CA、CB,分别在线段CA、CB上取中点D、E,连结DE,测得DE=35m,则可得A、B之间的距离为(??
)
A.?30m???????????????????????????????????B.?70m???????????????????????????????????C.?105m???????????????????????????????????D.?140m
4.如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20,那么△DEF的周长是(
??)
A.?20?????????????????????????????????????????B.?15?????????????????????????????????????????C.?10?????????????????????????????????????????D.?5
5.如图所示,?ABCD的对角线AC,BD相交于点O,点E是CD的中点,若BC=6,则OE的长为(?
)
A.?2??????????????????????????????????????????B.?2.5??????????????????????????????????????????C.?3??????????????????????????????????????????D.?4
6.如图,在△
中,
、
是△
的中线,
与
相交于点O,点F、
分别是
、
的中点,连结
.若
=6cm,
=8cm,则四边形DEFG的周长是(??
)
A.?14cm??????????????????????????????????B.?18
cm??????????????????????????????????C.?24cm??????????????????????????????????D.?28cm
7.如图,已知四边形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动而点R不动时,
那么下列结论成立的是(???
).
A.?线段EF的长逐渐增大??????B.?线段EF的长逐渐减少??????C.?线段EF的长不变??????D.?线段EF的长不能确定
8.如图,在四边形ABCD中,R,P分别是BC,CD上的点,E,F分别是AP,RP的中点,当点P在CD上从点C向点D移动而点R不动时,以下结论成立的是(??
)
A.?线段EF的长逐渐增大???????????????????????????????????????????B.?线段EF的长逐渐减小
C.?线段EF的长不变??????????????????????????????????????????????????D.?线段EF的长与点P的位置有关
9.如图,已知E,F,G,H分别为四边形ABCD各边的中点,若AC=10
cm,BD=12
cm,则四边形EFGH的周长为(??
)
A.?10
cm????????????????????????????????B.?11
cm????????????????????????????????C.?12
cm????????????????????????????????D.?22
cm
10.如图是一块等腰三角形空地ABC,已知点D,E分别是边AB,AC的中点,量得AC=10米,AB=BC=6米,若用篱笆围成四边形BCED来放养小鸡,则需要篱笆的长是(
??)
A.?22米????????????????????????????????????B.?17米????????????????????????????????????C.?14米????????????????????????????????????D.?11米
二、填空题
11.如图,在
中,
分别是
的中点,连接
,若
,则四边形
的周长是________.
12.已知三角形的周长为20cm,连接各边中点所得的三角形的周长为________cm.
13.如图,已知△ABC的周长为a,A1B1
,
B1C1
,
A1C1是△ABC的三条中位线,它们构成了△A1B1C1
,
△A2B2C2是由△A1B1C1的三条中位线A2B2
,
B2C2
,
A2C2构成的……如此进行下去,得到△AnBnCn
,
则△A1B1C1的周长为________,△A2B2C2的周长为________,△A3B3C3的周长为________,△AnBnCn的周长为________.
14.如图所示,在四边形ABCD中,AB=CD=4,M、N、P分别是AD、BC、BD的中点,∠ABD=20°,∠BDC=80°,则MN的长是________.
三、解答题
15.请叙述三角形中位线定理并证明.
16.如图,在△ABC中,已知AB=6,AC=10,AD平分∠BAC,BD⊥AD于点D,E为BC中点.求DE的长.
17.如图,在△ABC中,D是边BC上的中点,F是AD的中点,BF的延长线交AC于点E.求证:AE=
CE.
18.如图,在△ABC中,∠B=∠C,D为BC的中点,
E为AC的中点,AB=6,求DE的长。
19.阅读材料,解决问题:
明明家准备装修房子,房子的部分平面图如图1所示.为了增大房子的使用空间,爸爸想把现在两间卧室之间的非承重墙打掉,之后在打掉的位置做一排衣柜.
爸爸说:“我想测量一下非承重墙的厚度,从而知道打掉这堵墙后可以腾出多少空间.我手里有的工具是教学用量角器、大刻度尺,明明,你帮助爸爸看看应该怎样测量.”
“这堵墙的厚度处处相等吗?”明明说.
爸爸说:“这个没问题,当年收房的时候我就考察过.”
“那我就可以在地面上直接进行测量了.我再问您,每个房间中地面和墙的交线都是垂直或平行的吗?”明明说.
爸爸回答:“是的”.
“那就简单了.我们俩先测出客厅的东西向宽度,再测出每个卧室的东西向宽度,用客厅的宽度减去两个卧室的宽度就是中间这堵非承重墙的厚度.”明明说.
爸爸说:“那不行,客厅和卧室的家具摆得满满的,东西向宽度勉强测到也不准确.你能不能在不借助测量房间宽度或房间内其它家具的前提下,设计一个通过测量和计算得到非承重墙厚度的方案.”
请你利用学到的三角形或四边形的知识帮助明明解决此问题.
要求:(1)在图2中画出测量时用到的示意图,图形要规范;
(2)简要叙述测量过程;
(3)写出测量的依据.
答案解析部分
一、单选题
1.【答案】
B
【解析】【解答】解:∵D、E分别是△ABC的边AB、AC的中点,
∴DE是△ABC的中位线,
∴DE=
BC=3,
故答案为:B.
【分析】由已知可得DE是△ABC的中位线,再根据三角形的中位线等于第三边的一半,可求出DE的长。
2.【答案】
C
【解析】【解答】解:∵点D,E,F分别是边AB,BC,AC的中点,
∴AD=
AB=1,AF=
AC=1,DE、FE是△ABC的中位线,
∴DE=
AC=1,EF=
AB=1,
∴四边形ADEF的周长=AD+DE+EF+AF=4,
故答案为:C.
【分析】根据三角形中位线定理、线段中点的概念计算,得到答案.
3.【答案】
B
【解析】【解答】解:∵D、E分别是AC、BC的中点,
∴DE是△ABC的中位线,
根据三角形的中位线定理,得:AB=2DE=70m.
故答案为:B.
【分析】由D,E分别是边AC,AB的中点,首先判定DE是三角形的中位线,然后根据三角形的中位线定理求得AB的长即可.
4.【答案】
C
【解析】【解答】∵D、E分别是△ABC的边BC、AB的中点,
∴DE=
AC,同理
EF=
BC,DF=
AB,∴C△DEF=DE+EF+DF=
(AC+BC+AB)=
×20=10.
故答案为:C.
【分析】利用三角形的中位线定理得到线段的等量关系,再求出三角形的周长即可.
5.【答案】
C
【解析】【解答】解:∵?ABCD的对角线AC、BD相交于点O,
∴OB=OD,
∵点E是CD的中点,
∴CE=DE,
∴OE是△BCD的中位线,
∵BC=6,
∴OE=
BC=3.
故答案为:C.
【分析】先说明OE是△BCD的中位线,再根据三角形的中位线平行于第三边并且等于第三边的一半求解.
6.【答案】
A
【解析】【解答】解:∵点F、G分别是BO、CO的中点,BC
=
8cm
∴FG=
BC=4
cm
∵BD、CE是△ABC的中线
∴DE=
BC=4
cm
∵点F、G、E、D分别是BO、CO、AB、AC的中点,AO
=
6cm
∴EF=
AO=3
cm,DG=
AO=3
cm
∴四边形DEFG的周长=EF+FG+DG+DE=14?cm
故答案为:A
【分析】根据三角形的中位线定理得出FG=
BC=4
cm,DE=
BC=4
cm,点F、G、E、D分别是BO、CO、AB、AC的中点,AO
=
6cm,得出EF=
AO=3
cm,DG=
AO=3
cm,进而求出
四边形DEFG的周长
。
7.【答案】
C
【解析】【解答】解:如图,连接AR,
∵E、F分别是AP、RP的中点,
∴EF为△APR的中位线,
∴EF=
AR,为定值.
∴线段EF的长不改变.
故答案为:C.
【分析】因为R不动,所以AR不变.根据三角形中位线定理可得EF=
AR,因此线段EF的长不变.
8.【答案】
C
【解析】【解答】解:如图,连接AR,
∵E,F分别是AP,RP的中点
∴EF是△PAR的中位线,
∴EF=AR
∵当点P在CD上从点C向点D移动而点R不动,
∴线段EF的长不变,
故答案为:C
【分析】根据已知条件E,F分别是AP,RP的中点,因此连接AR,构造三角形的中位线,得出EF=AR,由于点R不动,因此AR是一个定值,即可得出答案。
9.【答案】
D
【解析】【解答】解:∵E、F分别是AB、BC的中点,
∴EF=AC=×10=5
同理可得:HG=AC=×10=5
EH=BD=×12=6
FG=BD=×12=6
∴四边形EFGH的周长=EF+HG+EH+FG=5+5+6+6=22
故答案为:D
【分析】根据三角形的中位线定理及已知条件分别求出EF、HG、EH、FG的长,再求出四边形EFGH的周长即可。
10.【答案】
B
【解析】【解答】由题意可知,点D,E分别是边AB,AC的中点,
?
?
?
,即
四边形BCED的周长
故答案为:B
【分析】利用三角形中位线定理求出DE的长,再利用线段中点的定义求出BD、CE的长,然后求出四边形BCDE的周长。
二、填空题
11.【答案】
22cm
【解析】【解答】解:∵
分别是
的中点,
,
∴
,
,
,
,
∴四边形
的周长为
,
故答案为:
.
【分析】通过线段中点和三角形的中位线可求出各边的长,然后即可求出四边形
的周长.
12.【答案】
10
【解析】【解答】解:如图,
∵
分别为
的中点,
∴
,
∵
,
∴
,
故答案为:10.
【分析】根据中位线定理分别求出DE、EF和DF各边的长,则△DEF的周长可求.
13.【答案】
;;;a2n
【解析】【解答】解:∵A1B1
,
B1C1
,
A1C1是△ABC的三条中位线,
∴A1B1=AB,A1C1=AC,C1B1=CB,
∴△A1B1C1的周长=(AB+AC+CB)=a.
同理:A2B2C2的周长为a,△A3B3C3的周长为a,△AnBnCn的周长为.
【分析】根据中位线定理可知,△A1B1C1的周长为
,△A2B2C2的周长为
·
=
……△AnBnCn的周长为
.
14.【答案】
2
【解析】【解答】解:作PH⊥MN于H,
∵M、N、P分别是AD、BC、BD的中点,
∴PM=
AB=2,PN=
CD=2,PM∥AB,PN∥CD,
∴∠MPD=∠ABD=20°,∠BPN=∠BDC=80°,PM=PN,
∴∠MPN=120°,
∵PM=PN,
∴∠PMN=30°,MH=HN,
∴PH=
PM=1,
由勾股定理得,MH=
=
,
∴MN=2MH=2
,
故答案为:2
.
【分析】作PH⊥MN于H,根据三角形中位线定理求出PM、PN、∠MPN,根据等腰三角形的性质、勾股定理计算即可.
三、解答题
15.【答案】
解:已知:△ABC中,点E、F分别是AB、AC的中点,
求证:三角形的中位线平行于第三边并且等于第三边的一半,
证明:如图,延长EF到D,使FD=EF,
∵点F是AC的中点,
∴AF=CF,
在△AEF和△CDF中,
,
∴△AEF≌△CDF(SAS),
∴AE=CD,∠D=∠AEF,
∴AB∥CD,
∵点E是AB的中点,
∴AE=BE,
∴BE=CD,
∴BE∥CD,BE=CD
∴四边形BCDE是平行四边形,
∴DE∥BC,DE=BC,
∴DE∥BC且DE=
BC.
【解析】【分析】作出图形,然后写出已知、求证,延长EF到D,使FD=EF,利用“边角边”证明△AEF和△CDF全等,根据全等三角形对应边相等可得AE=CD,全等三角形对应角相等可得∠D=∠AEF,再求出CE=CD,根据内错角相等,两直线平行判断出AB∥CD,然后判断出四边形BCDE是平行四边形,根据平行四边形的性质可得DE∥BC,DE=BC.
16.【答案】
解:延长BD交AC于点F.∵∠BAD=∠FAD,AD=AD,∠ADB=∠ADF=90°.∴△ABD≌△AFD,∴AB=AF=6,BD=DF.又∵E为BC中点,∴DE=
FC=
(AC-AF)=
(10-6)=2
【解析】【分析】延长BD交AC于点F.由已知条件可用角边角证得△ABD≌△AFD,所以AB=AF=6,BD=DF.而E为BC中点,所以DE是三角形BCF的中位线,根据三角形的中位线定理可得DE=?FC=?(AC-AF)=?(10-6)=2。
17.【答案】
解:取BE的中点G,连结DG.∵D,G分别是BC,BE的中点,∴DG是△BCE的中位线,∴DG∥AC,DG=
CE.∴∠FAE=∠FDG,∠AEF=∠DGF.∵F是AD的中点,∴AF=DF.∴△AEF≌△DGF(AAS).∴AE=DG.∴AE=
CE
【解析】【分析】取BE的中点G,连结DG.因为D是边BC上的中点,所以根据三角形的中位线定理可得DG∥AC,DG=?
CE,由平行线的性质可得∠FAE=∠FDG,∠AEF=∠DGF,因为F是AD的中点,所以AF=DF.用角角边可证△AEF≌△DGF,所以AE=DG.即AE=?CE。
18.【答案】
解:∵D为BC的中点,E为AC的中点,
∴DE为△ABC的中位线,
∴DE=
AB=12×6=3.
【解析】【分析】根据三角形的中位线定理直接求出得到DE=AB.
19.【答案】
如图,在椭圆垛的两边测出AC=BD,过点C、D作出CE⊥AC、DF⊥BD,可知E、C、D、F在一条直线上,同时测出EC、DF的长,在客厅内找一点P,连接PE、PF,通过测量找得PE、PF的中点M、N,测出MN的长,根据三角形的中位线定理即可得EF的长,用EF的长减去EC、DF的长即可得CD的长.
【解析】【分析】根据非承重墙的一端存在椭圆垛,需要三角形或四边形,测出AC=BD,再得出EC、DF的长,根据中位线定理得出EF的长度,最后得出CD的长.
(
第
一
页
共
1
页
)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
