第五章 5.3.1 函数的单调性学案2020-2021学年高二下学期数学人教A版(2019)选择性必修第二册 Word含解析
文档属性
| 名称 | 第五章 5.3.1 函数的单调性学案2020-2021学年高二下学期数学人教A版(2019)选择性必修第二册 Word含解析 |  | |
| 格式 | docx | ||
| 文件大小 | 390.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-13 23:36:41 | ||
图片预览




文档简介
§5.3 导数在研究函数中的应用
5.3.1 函数的单调性
学习目标 1.了解导数与函数的单调性的关系.2.掌握利用导数判断函数单调性的方法.3.能利用导数求不超过三次多项式函数的单调区间.
知识点一 函数的单调性与其导数的正负之间的关系
定义在区间(a,b)内的函数y=f(x):
f′(x)的正负
f(x)的单调性
f′(x)>0
单调递增
f′(x)<0
单调递减
思考 如果在某个区间内恒有f′(x)=0,那么函数f(x)有什么特性?
答案 f(x)是常数函数.
知识点二 利用导数判断函数的单调性的一般步骤
(1)确定函数y=f(x)的定义域;
(2)求出导数f′(x)的零点;
(3)用f′(x)的零点将f(x)的定义域划分为若干个区间,列表给出f′(x)在各区间上的正负,由此得出函数y=f(x)在定义域内的单调性.
知识点三 函数图象的变化趋势与导数的绝对值的大小的关系
一般地,设函数y=f(x),在区间(a,b)上:
导数的绝对值
函数值变化
函数的图象
越大
快
比较“陡峭”(向上或向下)
越小
慢
比较“平缓”(向上或向下)
1.函数f(x)在定义域上都有f′(x)<0,则函数f(x)在定义域上单调递减.( )
2.函数f(x)在某区间内单调递增,则一定有f′(x)>0.( )
3.函数在某个区间上变化越快,函数在这个区间上的导数的绝对值越大.( )
4.函数y=x3+x的单调递增区间为(-∞,+∞).( )
一、函数图象与导函数图象的关系
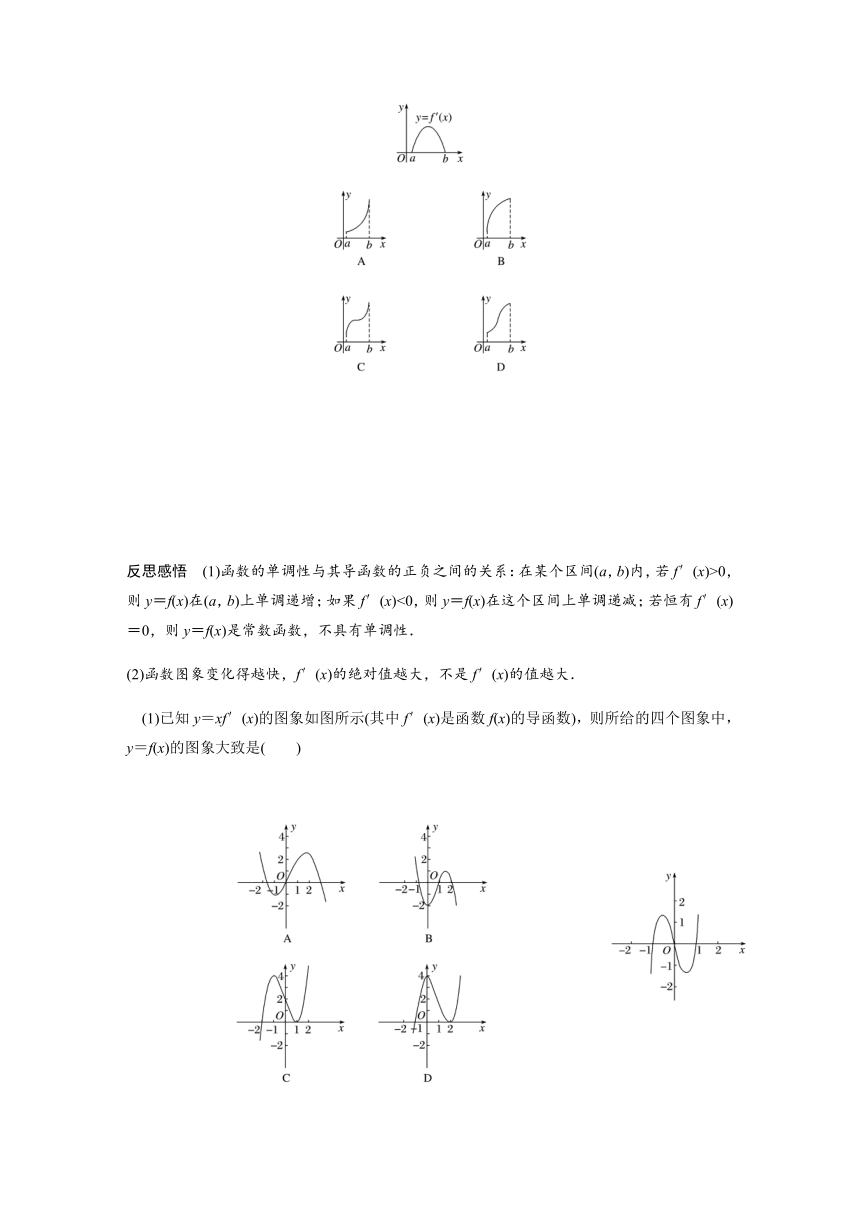
例1 (1)设函数f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能为( )
(2)已知f′(x)是f(x)的导函数,f′(x)的图象如图所示,则f(x)的图象只可能是( )
反思感悟 (1)函数的单调性与其导函数的正负之间的关系:在某个区间(a,b)内,若f′(x)>0,则y=f(x)在(a,b)上单调递增;如果f′(x)<0,则y=f(x)在这个区间上单调递减;若恒有f′(x)=0,则y=f(x)是常数函数,不具有单调性.
(2)函数图象变化得越快,f′(x)的绝对值越大,不是f′(x)的值越大.
(1)已知y=xf′(x)的图象如图所示(其中f′(x)是函数f(x)的导函数),则所给的四个图象中,y=f(x)的图象大致是( )
(2)函数y=f(x)在定义域内可导,其图象如图,记y=f(x)的导函数为y=f′(x),则不等式f′(x)<0的解集为__________________.
二、利用导数求函数的单调区间
例2 求下列函数的单调区间:
(1)f(x)=x2-ln
x;(2)f(x)=x+(b>0).
反思感悟 求函数y=f(x)的单调区间常用解不等式f′(x)<0,函数在解集与定义域的交集上单调递减.解不等式f′(x)>0,函数在解集与定义域的交集上为单调递增.
跟踪训练2 (1)函数f(x)=(x2+2x)ex(x∈R)的单调递减区间为__________________.
(2)设函数f(x)=ex-ax-2,求f(x)的单调区间.
利用导数求参数的取值范围
典例 已知函数f(x)=x3-ax-1为增函数,求实数a的取值范围.
[素养提升] (1)利用导数法解决取值范围问题的两个基本思路
①将问题转化为不等式在某区间上的恒成立问题,即f′(x)≥0(或f′(x)≤0)恒成立,利用分离参数或函数性质求解参数范围,然后检验参数取“=”时是否满足题意.
②先令f′(x)>0(或f′(x)<0),求出参数的取值范围后,再验证参数取“=”时f(x)是否满足题意.
(2)理清运算对象,选择运算方法,求得运算结果,充分体现数学运算的数学核心素养.
1.设函数f(x)的图象如图所示,则导函数f′(x)的图象可能为( )
2.(多选)函数f(x)=(x-3)ex在下列区间上单调递增的是( )
A.(-∞,2)
B.(0,3)
C.(3,4)
D.(2,+∞)
3.函数f(x)=ax3-x在R上为减函数,则( )
A.a≤0
B.a<1
C.a<2
D.a≤
4.若函数f(x)=x3-2ax2-(a-2)x+5恰好有三个单调区间,则实数a的取值范围为( )
A.-1≤a≤2
B.-2≤a≤1
C.a>2或a<-1
D.a>1或a<-2
5.若f(x)=-x2+bln(x+2)在(-1,+∞)上单调递减,则b的取值范围是________.
1.知识清单:
(1)函数的单调性与其导数的关系.
(2)利用导数判断函数的单调性.
(3)利用导数求函数的单调区间.
2.方法归纳:方程思想、分类讨论.
3.常见误区:利用导数法解决取值范围问题时忽略等号是否满足;忽略定义域的限制.
1.(多选)如图是函数y=f(x)的导函数f′(x)的图象,则下列判断正确的是( )
A.在区间(-2,1)上,f(x)单调递增
B.在(1,2)上,f(x)单调递增
C.在(4,5)上,f(x)单调递增
D.在(-3,-2)上,f(x)单调递增
2.函数f(x)=x3-3x2+1的单调递减区间为( )
A.(2,+∞)
B.(-∞,2)
C.(-∞,0)
D.(0,2)
3.函数f(x)=ln
x-4x+1的单调递增区间为( )
A.
B.(0,4)
C.
D.
4.(多选)函数f(x)=xe-x的单调递增区间可以是( )
A.[-1,0]
B.[2,8]
C.[1,2]
D.[0,1]
5.函数f(x)=xcos
x的导函数f′(x)在区间[-π,π]上的图象大致是( )
6.函数f(x)=(x2+x+1)ex的单调递减区间为________________.
7.函数f(x)的图象如图所示,f′(x)为函数f(x)的导函数,则不等式<0的解集为______________.
8.若函数f(x)=(x2+mx)ex的单调递减区间是,则实数m的值为______________,函数f(x)的单调递增区间是________________.
9.试求函数f(x)=kx-ln
x的单调区间.
10.已知函数f(x)=x3+ax2-a2x+2.
(1)若a=1,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若a>0,求函数f(x)的单调区间.
11.已知函数f(x)=x2-ax+3在(0,1)上为单调递减,函数g(x)=x2-aln
x在(1,2)上为单调递增,则a等于( )
A.1
B.2
C.0
D.
12.设f(x),g(x)是定义在R上的恒大于0的可导函数,且f′(x)g(x)-f(x)g′(x)<0,则当aA.f(x)g(x)>f(b)g(b)
B.f(x)g(a)>f(a)g(x)
C.f(x)g(b)>f(b)g(x)
D.f(x)g(x)>f(a)g(a)
13.已知函数f(x)=x3-12x,若f(x)在区间(2m,m+1)上单调递减,则实数m的取值范围是________.
14.已知函数f(x)是R上的偶函数,且在(0,+∞)上有f′(x)>0,若f(-1)=0,则关于x的不等式xf(x)<0的解集是________________.
15.(多选)已知f(x)为(0,+∞)上的可导函数,且(x+1)·f′(x)>f(x),则下列不等式一定成立的是( )
A.3f(4)<4f(3)
B.4f(4)>5f(3)
C.3f(3)<4f(2)
D.3f(3)>4f(2)
16.已知函数f(x)=ax2+ln(x+1).
(1)当a=-时,求函数f(x)的单调区间;
(2)若函数f(x)在区间[1,+∞)上为单调递减,求实数a的取值范围.
参考答案
×
×
√
√
例1(1)答案 D
解析 由函数的图象可知:当x<0时,函数单调递增,导数始终为正;当x>0时,函数先增后减再增,即导数先正后负再正,对照选项,应选D.
(2)答案 D
解析 从f′(x)的图象可以看出,在区间内,导数单调递增;在区间内,导数单调递减.
即函数f(x)的图象在内越来越陡,
在内越来越平缓,由此可知,只有选项D符合.
跟踪训练1(1)答案 C
解析 当0∴f′(x)<0,故y=f(x)在(0,1)上单调递减;
当x>1时,xf′(x)>0,∴f′(x)>0,
故y=f(x)在(1,+∞)上单调递增.
故选C.
(2)答案 ∪(2,3)
解析 因为y=f(x)在区间和区间(2,3)上单调递减,所以在区间和区间(2,3)上f′(x)<0.
跟踪训练2 (1)答案 (-2-,-2+)
解析 由f′(x)=(x2+4x+2)ex<0,
即x2+4x+2<0,
解得-2-所以f(x)=(x2+2x)ex的单调递减区间为
(-2-,-2+).
(2)解 f(x)的定义域为(-∞,+∞),f′(x)=ex-a.
若a≤0,则f′(x)>0,
所以f(x)在(-∞,+∞)上单调递增.
若a>0,则当x∈(-∞,ln
a)时,f′(x)<0;
当x∈(ln
a,+∞)时,f′(x)>0.
所以f(x)在(-∞,ln
a)上单调递减,在(ln
a,+∞)上单调递增.
综上所述,当a≤0时,函数f(x)的单调递增区间为(-∞,+∞),无单调递减区间;
当a>0时,f(x)的单调递减区间为(-∞,ln
a),单调递增区间为(ln
a,+∞).
解 由已知得f′(x)=3x2-a,
因为f(x)在(-∞,+∞)上是增函数,
所以f′(x)=3x2-a≥0在(-∞,+∞)上恒成立,
即a≤3x2对x∈R恒成立,
因为3x2≥0,所以只需a≤0.
又因为a=0时,f′(x)=3x2≥0,
即f(x)=x3-1在R上是增函数,所以a≤0.
1.答案 C
解析 ∵f(x)在(-∞,1),(4,+∞)上单调递减,在(1,4)上是单调递增,∴当x<1或x>4时,f′(x)<0;
当1<x<4时,f′(x)>0.
2.答案 CD
解析 ∵f′(x)=ex+(x-3)ex=(x-2)ex,
由f′(x)>0得(x-2)ex>0,∴x>2.
∴f(x)的单调递增区间为(2,+∞),CD符合.
3.答案 A
解析 f′(x)=3ax2-1≤0恒成立,
∴a≤0.
4.答案 D
解析 若函数f(x)有3个单调区间,
则f
′(x)=4x2-4ax-(a-2)有2个零点,
故Δ=16a2+16(a-2)>0,
解得a>1或a<-2.
5.答案 (-∞,-1]
解析 ∵f(x)在(-1,+∞)上单调递减,
∴f′(x)≤0在(-1,+∞)上恒成立.
∵f′(x)=-x+,
∴-x+≤0在(-1,+∞)上恒成立,
即b≤x(x+2)在(-1,+∞)上恒成立.
设g(x)=x(x+2)=(x+1)2-1,
则当x>-1时,g(x)>-1,∴b≤-1.
1.答案 BC
解析 由题图知当x∈(1,2),x∈(4,5)时,f′(x)>0,所以在(1,2),(4,5)上,f(x)是单调递增,当x∈(-3,-2)时,f′(x)<0,所以在(-3,-2)上,f(x)是单调递减.
2.答案 D
解析 f′(x)=3x2-6x=3x(x-2),令f′(x)<0,得03.答案 A
解析 f(x)=ln
x-4x+1的定义域是{x|x>0},f′(x)=-4=,当f′(x)>0时,解得04.答案 AD
解析 由f′(x)=e-x-x·e-x=(1-x)·e-x>0,
e-x>0,得x<1.
5.答案 A
解析 因为f(x)=xcos
x,所以f′(x)=cos
x-xsin
x.
因为f′(-x)=f′(x),
所以f′(x)为偶函数,
所以函数图象关于y轴对称.
由f′(0)=1可排除C,D.
而f′(1)=cos
1-sin
1<0,排除B.
6.答案 (-2,-1)
解析 f′(x)=(2x+1)ex+(x2+x+1)ex=ex(x2+3x+2)=ex(x+1)(x+2),
令f′(x)<0,解得-2所以函数f(x)的单调递减区间为(-2,-1).
7.答案 (-3,-1)∪(0,1)
解析 由题图知,当x∈(-∞,-3)∪(-1,1)时,
f′(x)<0;
当x∈(-3,-1)∪(1,+∞)时,f′(x)>0,
故不等式<0的解集为(-3,-1)∪(0,1).
8.答案 - ,(1,+∞)
解析 f′(x)=[x2+(m+2)x+m]ex,
因为f(x)的单调递减区间是,
所以f′(x)=0的两个根分别为x1=-,x2=1,
即解得m=-.
由f′(x)=ex
=(x-1)(2x+3)ex,
得f′(x)>0时,x<-或x>1.
9.解 函数f(x)=kx-ln
x的定义域为(0,+∞),
f′(x)=k-=.
当k≤0时,kx-1<0,∴f′(x)<0,则f(x)在(0,+∞)上单调递减.
当k>0时,由f′(x)<0,即<0,解得0由f′(x)>0,即>0,解得x>.
∴当k>0时,f(x)的单调递减区间为,
单调递增区间为.
综上所述,当k≤0时,f(x)的单调递减区间为(0,+∞),无单调递增区间;
当k>0时,f(x)的单调递减区间为,单调递增区间为.
10.解 (1)∵a=1,∴f(x)=x3+x2-x+2,
∴f′(x)=3x2+2x-1,∴f′(1)=4.又f(1)=3,
∴切点坐标为(1,3),∴所求切线方程为y-3=4(x-1),
即4x-y-1=0.
(2)f′(x)=3x2+2ax-a2=(x+a)(3x-a),
由f′(x)=0得x=-a或x=.
又a>0,由f′(x)<0,得-a由f′(x)>0,得x<-a或x>,
故f(x)的单调递减区间为,单调递增区间为(-∞,-a)和.
11.答案 B
解析 因为函数f(x)=x2-ax+3在(0,1)上单调递减,
所以≥1,解得a≥2.g′(x)=2x-,
依题意得,g′(x)≥0在(1,2)上恒成立,
即2x2≥a在(1,2)上恒成立,故a≤2.所以a=2.
12.答案 C
解析 因为′=.
又因为f′(x)g(x)-f(x)g′(x)<0,所以在R上为减函数.
又因为a>,
又因为f(x)>0,g(x)>0,所以f(x)g(b)>f(b)g(x).
13.答案 [-1,1)
解析 令f′(x)≤0,即3x2-12≤0,解得-2≤x≤2.∴f(x)的单调递减区间为[-2,2],
由题意得(2m,m+1)?[-2,2],
∴解得-1≤m<1.
14.答案 (-∞,-1)∪(0,1)
解析 因为在(0,+∞)上f′(x)>0,
所以f(x)在(0,+∞)上单调递增,
又f(x)为偶函数,
所以f(-1)=f(1)=0,
且f(x)在(-∞,0)上单调递减,
f(x)的草图如图所示,
所以xf(x)<0的解集为(-∞,-1)∪(0,1).
15.答案 BD
解析 由(x+1)f′(x)>f(x),
得(x+1)f′(x)-f(x)>0,
令g(x)=,则g′(x)=>0,
∴g(x)在(0,+∞)上单调递增,∴g(2)则<<,
即4f(2)<3f(3),5f(3)<4f(4),故选BD.
16.解 (1)当a=-时,
f(x)=-x2+ln(x+1)(x>-1),
f′(x)=-x+=-(x>-1).
当f′(x)>0时,解得-1当f′(x)<0时,解得x>1.
故函数f(x)的单调递增区间是(-1,1),单调递减区间是(1,+∞).
(2)因为函数f(x)在区间[1,+∞)上单调递减,
所以f′(x)=2ax+≤0对任意x∈[1,+∞)恒成立,
即a≤-对任意x∈[1,+∞)恒成立.
令g(x)=-,x∈[1,+∞),
易求得在区间[1,+∞)上g′(x)>0,
故g(x)在区间[1,+∞)上单调递增,
故g(x)min=g(1)=-,故a≤-.
即实数a的取值范围为.
5.3.1 函数的单调性
学习目标 1.了解导数与函数的单调性的关系.2.掌握利用导数判断函数单调性的方法.3.能利用导数求不超过三次多项式函数的单调区间.
知识点一 函数的单调性与其导数的正负之间的关系
定义在区间(a,b)内的函数y=f(x):
f′(x)的正负
f(x)的单调性
f′(x)>0
单调递增
f′(x)<0
单调递减
思考 如果在某个区间内恒有f′(x)=0,那么函数f(x)有什么特性?
答案 f(x)是常数函数.
知识点二 利用导数判断函数的单调性的一般步骤
(1)确定函数y=f(x)的定义域;
(2)求出导数f′(x)的零点;
(3)用f′(x)的零点将f(x)的定义域划分为若干个区间,列表给出f′(x)在各区间上的正负,由此得出函数y=f(x)在定义域内的单调性.
知识点三 函数图象的变化趋势与导数的绝对值的大小的关系
一般地,设函数y=f(x),在区间(a,b)上:
导数的绝对值
函数值变化
函数的图象
越大
快
比较“陡峭”(向上或向下)
越小
慢
比较“平缓”(向上或向下)
1.函数f(x)在定义域上都有f′(x)<0,则函数f(x)在定义域上单调递减.( )
2.函数f(x)在某区间内单调递增,则一定有f′(x)>0.( )
3.函数在某个区间上变化越快,函数在这个区间上的导数的绝对值越大.( )
4.函数y=x3+x的单调递增区间为(-∞,+∞).( )
一、函数图象与导函数图象的关系
例1 (1)设函数f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能为( )
(2)已知f′(x)是f(x)的导函数,f′(x)的图象如图所示,则f(x)的图象只可能是( )
反思感悟 (1)函数的单调性与其导函数的正负之间的关系:在某个区间(a,b)内,若f′(x)>0,则y=f(x)在(a,b)上单调递增;如果f′(x)<0,则y=f(x)在这个区间上单调递减;若恒有f′(x)=0,则y=f(x)是常数函数,不具有单调性.
(2)函数图象变化得越快,f′(x)的绝对值越大,不是f′(x)的值越大.
(1)已知y=xf′(x)的图象如图所示(其中f′(x)是函数f(x)的导函数),则所给的四个图象中,y=f(x)的图象大致是( )
(2)函数y=f(x)在定义域内可导,其图象如图,记y=f(x)的导函数为y=f′(x),则不等式f′(x)<0的解集为__________________.
二、利用导数求函数的单调区间
例2 求下列函数的单调区间:
(1)f(x)=x2-ln
x;(2)f(x)=x+(b>0).
反思感悟 求函数y=f(x)的单调区间常用解不等式f′(x)<0,函数在解集与定义域的交集上单调递减.解不等式f′(x)>0,函数在解集与定义域的交集上为单调递增.
跟踪训练2 (1)函数f(x)=(x2+2x)ex(x∈R)的单调递减区间为__________________.
(2)设函数f(x)=ex-ax-2,求f(x)的单调区间.
利用导数求参数的取值范围
典例 已知函数f(x)=x3-ax-1为增函数,求实数a的取值范围.
[素养提升] (1)利用导数法解决取值范围问题的两个基本思路
①将问题转化为不等式在某区间上的恒成立问题,即f′(x)≥0(或f′(x)≤0)恒成立,利用分离参数或函数性质求解参数范围,然后检验参数取“=”时是否满足题意.
②先令f′(x)>0(或f′(x)<0),求出参数的取值范围后,再验证参数取“=”时f(x)是否满足题意.
(2)理清运算对象,选择运算方法,求得运算结果,充分体现数学运算的数学核心素养.
1.设函数f(x)的图象如图所示,则导函数f′(x)的图象可能为( )
2.(多选)函数f(x)=(x-3)ex在下列区间上单调递增的是( )
A.(-∞,2)
B.(0,3)
C.(3,4)
D.(2,+∞)
3.函数f(x)=ax3-x在R上为减函数,则( )
A.a≤0
B.a<1
C.a<2
D.a≤
4.若函数f(x)=x3-2ax2-(a-2)x+5恰好有三个单调区间,则实数a的取值范围为( )
A.-1≤a≤2
B.-2≤a≤1
C.a>2或a<-1
D.a>1或a<-2
5.若f(x)=-x2+bln(x+2)在(-1,+∞)上单调递减,则b的取值范围是________.
1.知识清单:
(1)函数的单调性与其导数的关系.
(2)利用导数判断函数的单调性.
(3)利用导数求函数的单调区间.
2.方法归纳:方程思想、分类讨论.
3.常见误区:利用导数法解决取值范围问题时忽略等号是否满足;忽略定义域的限制.
1.(多选)如图是函数y=f(x)的导函数f′(x)的图象,则下列判断正确的是( )
A.在区间(-2,1)上,f(x)单调递增
B.在(1,2)上,f(x)单调递增
C.在(4,5)上,f(x)单调递增
D.在(-3,-2)上,f(x)单调递增
2.函数f(x)=x3-3x2+1的单调递减区间为( )
A.(2,+∞)
B.(-∞,2)
C.(-∞,0)
D.(0,2)
3.函数f(x)=ln
x-4x+1的单调递增区间为( )
A.
B.(0,4)
C.
D.
4.(多选)函数f(x)=xe-x的单调递增区间可以是( )
A.[-1,0]
B.[2,8]
C.[1,2]
D.[0,1]
5.函数f(x)=xcos
x的导函数f′(x)在区间[-π,π]上的图象大致是( )
6.函数f(x)=(x2+x+1)ex的单调递减区间为________________.
7.函数f(x)的图象如图所示,f′(x)为函数f(x)的导函数,则不等式<0的解集为______________.
8.若函数f(x)=(x2+mx)ex的单调递减区间是,则实数m的值为______________,函数f(x)的单调递增区间是________________.
9.试求函数f(x)=kx-ln
x的单调区间.
10.已知函数f(x)=x3+ax2-a2x+2.
(1)若a=1,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若a>0,求函数f(x)的单调区间.
11.已知函数f(x)=x2-ax+3在(0,1)上为单调递减,函数g(x)=x2-aln
x在(1,2)上为单调递增,则a等于( )
A.1
B.2
C.0
D.
12.设f(x),g(x)是定义在R上的恒大于0的可导函数,且f′(x)g(x)-f(x)g′(x)<0,则当a
B.f(x)g(a)>f(a)g(x)
C.f(x)g(b)>f(b)g(x)
D.f(x)g(x)>f(a)g(a)
13.已知函数f(x)=x3-12x,若f(x)在区间(2m,m+1)上单调递减,则实数m的取值范围是________.
14.已知函数f(x)是R上的偶函数,且在(0,+∞)上有f′(x)>0,若f(-1)=0,则关于x的不等式xf(x)<0的解集是________________.
15.(多选)已知f(x)为(0,+∞)上的可导函数,且(x+1)·f′(x)>f(x),则下列不等式一定成立的是( )
A.3f(4)<4f(3)
B.4f(4)>5f(3)
C.3f(3)<4f(2)
D.3f(3)>4f(2)
16.已知函数f(x)=ax2+ln(x+1).
(1)当a=-时,求函数f(x)的单调区间;
(2)若函数f(x)在区间[1,+∞)上为单调递减,求实数a的取值范围.
参考答案
×
×
√
√
例1(1)答案 D
解析 由函数的图象可知:当x<0时,函数单调递增,导数始终为正;当x>0时,函数先增后减再增,即导数先正后负再正,对照选项,应选D.
(2)答案 D
解析 从f′(x)的图象可以看出,在区间内,导数单调递增;在区间内,导数单调递减.
即函数f(x)的图象在内越来越陡,
在内越来越平缓,由此可知,只有选项D符合.
跟踪训练1(1)答案 C
解析 当0
当x>1时,xf′(x)>0,∴f′(x)>0,
故y=f(x)在(1,+∞)上单调递增.
故选C.
(2)答案 ∪(2,3)
解析 因为y=f(x)在区间和区间(2,3)上单调递减,所以在区间和区间(2,3)上f′(x)<0.
跟踪训练2 (1)答案 (-2-,-2+)
解析 由f′(x)=(x2+4x+2)ex<0,
即x2+4x+2<0,
解得-2-
(-2-,-2+).
(2)解 f(x)的定义域为(-∞,+∞),f′(x)=ex-a.
若a≤0,则f′(x)>0,
所以f(x)在(-∞,+∞)上单调递增.
若a>0,则当x∈(-∞,ln
a)时,f′(x)<0;
当x∈(ln
a,+∞)时,f′(x)>0.
所以f(x)在(-∞,ln
a)上单调递减,在(ln
a,+∞)上单调递增.
综上所述,当a≤0时,函数f(x)的单调递增区间为(-∞,+∞),无单调递减区间;
当a>0时,f(x)的单调递减区间为(-∞,ln
a),单调递增区间为(ln
a,+∞).
解 由已知得f′(x)=3x2-a,
因为f(x)在(-∞,+∞)上是增函数,
所以f′(x)=3x2-a≥0在(-∞,+∞)上恒成立,
即a≤3x2对x∈R恒成立,
因为3x2≥0,所以只需a≤0.
又因为a=0时,f′(x)=3x2≥0,
即f(x)=x3-1在R上是增函数,所以a≤0.
1.答案 C
解析 ∵f(x)在(-∞,1),(4,+∞)上单调递减,在(1,4)上是单调递增,∴当x<1或x>4时,f′(x)<0;
当1<x<4时,f′(x)>0.
2.答案 CD
解析 ∵f′(x)=ex+(x-3)ex=(x-2)ex,
由f′(x)>0得(x-2)ex>0,∴x>2.
∴f(x)的单调递增区间为(2,+∞),CD符合.
3.答案 A
解析 f′(x)=3ax2-1≤0恒成立,
∴a≤0.
4.答案 D
解析 若函数f(x)有3个单调区间,
则f
′(x)=4x2-4ax-(a-2)有2个零点,
故Δ=16a2+16(a-2)>0,
解得a>1或a<-2.
5.答案 (-∞,-1]
解析 ∵f(x)在(-1,+∞)上单调递减,
∴f′(x)≤0在(-1,+∞)上恒成立.
∵f′(x)=-x+,
∴-x+≤0在(-1,+∞)上恒成立,
即b≤x(x+2)在(-1,+∞)上恒成立.
设g(x)=x(x+2)=(x+1)2-1,
则当x>-1时,g(x)>-1,∴b≤-1.
1.答案 BC
解析 由题图知当x∈(1,2),x∈(4,5)时,f′(x)>0,所以在(1,2),(4,5)上,f(x)是单调递增,当x∈(-3,-2)时,f′(x)<0,所以在(-3,-2)上,f(x)是单调递减.
2.答案 D
解析 f′(x)=3x2-6x=3x(x-2),令f′(x)<0,得0
解析 f(x)=ln
x-4x+1的定义域是{x|x>0},f′(x)=-4=,当f′(x)>0时,解得0
解析 由f′(x)=e-x-x·e-x=(1-x)·e-x>0,
e-x>0,得x<1.
5.答案 A
解析 因为f(x)=xcos
x,所以f′(x)=cos
x-xsin
x.
因为f′(-x)=f′(x),
所以f′(x)为偶函数,
所以函数图象关于y轴对称.
由f′(0)=1可排除C,D.
而f′(1)=cos
1-sin
1<0,排除B.
6.答案 (-2,-1)
解析 f′(x)=(2x+1)ex+(x2+x+1)ex=ex(x2+3x+2)=ex(x+1)(x+2),
令f′(x)<0,解得-2
7.答案 (-3,-1)∪(0,1)
解析 由题图知,当x∈(-∞,-3)∪(-1,1)时,
f′(x)<0;
当x∈(-3,-1)∪(1,+∞)时,f′(x)>0,
故不等式<0的解集为(-3,-1)∪(0,1).
8.答案 - ,(1,+∞)
解析 f′(x)=[x2+(m+2)x+m]ex,
因为f(x)的单调递减区间是,
所以f′(x)=0的两个根分别为x1=-,x2=1,
即解得m=-.
由f′(x)=ex
=(x-1)(2x+3)ex,
得f′(x)>0时,x<-或x>1.
9.解 函数f(x)=kx-ln
x的定义域为(0,+∞),
f′(x)=k-=.
当k≤0时,kx-1<0,∴f′(x)<0,则f(x)在(0,+∞)上单调递减.
当k>0时,由f′(x)<0,即<0,解得0
∴当k>0时,f(x)的单调递减区间为,
单调递增区间为.
综上所述,当k≤0时,f(x)的单调递减区间为(0,+∞),无单调递增区间;
当k>0时,f(x)的单调递减区间为,单调递增区间为.
10.解 (1)∵a=1,∴f(x)=x3+x2-x+2,
∴f′(x)=3x2+2x-1,∴f′(1)=4.又f(1)=3,
∴切点坐标为(1,3),∴所求切线方程为y-3=4(x-1),
即4x-y-1=0.
(2)f′(x)=3x2+2ax-a2=(x+a)(3x-a),
由f′(x)=0得x=-a或x=.
又a>0,由f′(x)<0,得-a
故f(x)的单调递减区间为,单调递增区间为(-∞,-a)和.
11.答案 B
解析 因为函数f(x)=x2-ax+3在(0,1)上单调递减,
所以≥1,解得a≥2.g′(x)=2x-,
依题意得,g′(x)≥0在(1,2)上恒成立,
即2x2≥a在(1,2)上恒成立,故a≤2.所以a=2.
12.答案 C
解析 因为′=.
又因为f′(x)g(x)-f(x)g′(x)<0,所以在R上为减函数.
又因为a
又因为f(x)>0,g(x)>0,所以f(x)g(b)>f(b)g(x).
13.答案 [-1,1)
解析 令f′(x)≤0,即3x2-12≤0,解得-2≤x≤2.∴f(x)的单调递减区间为[-2,2],
由题意得(2m,m+1)?[-2,2],
∴解得-1≤m<1.
14.答案 (-∞,-1)∪(0,1)
解析 因为在(0,+∞)上f′(x)>0,
所以f(x)在(0,+∞)上单调递增,
又f(x)为偶函数,
所以f(-1)=f(1)=0,
且f(x)在(-∞,0)上单调递减,
f(x)的草图如图所示,
所以xf(x)<0的解集为(-∞,-1)∪(0,1).
15.答案 BD
解析 由(x+1)f′(x)>f(x),
得(x+1)f′(x)-f(x)>0,
令g(x)=,则g′(x)=>0,
∴g(x)在(0,+∞)上单调递增,∴g(2)
即4f(2)<3f(3),5f(3)<4f(4),故选BD.
16.解 (1)当a=-时,
f(x)=-x2+ln(x+1)(x>-1),
f′(x)=-x+=-(x>-1).
当f′(x)>0时,解得-1
故函数f(x)的单调递增区间是(-1,1),单调递减区间是(1,+∞).
(2)因为函数f(x)在区间[1,+∞)上单调递减,
所以f′(x)=2ax+≤0对任意x∈[1,+∞)恒成立,
即a≤-对任意x∈[1,+∞)恒成立.
令g(x)=-,x∈[1,+∞),
易求得在区间[1,+∞)上g′(x)>0,
故g(x)在区间[1,+∞)上单调递增,
故g(x)min=g(1)=-,故a≤-.
即实数a的取值范围为.
