9.2.3 总体集中趋势的估计课件(共37张PPT)2020-2021学年高一数学人教A版(2019)必修第二册第九章统计
文档属性
| 名称 | 9.2.3 总体集中趋势的估计课件(共37张PPT)2020-2021学年高一数学人教A版(2019)必修第二册第九章统计 |  | |
| 格式 | pptx | ||
| 文件大小 | 625.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-14 08:19:17 | ||
图片预览










文档简介
9.2.3 总体集中趋势的估计
课标定位
素养阐释
1.结合实例,能用样本估计总体的集中趋势参数(平均数、中位数、众数).
2.会求样本数据的平均数、中位数、众数并理解它们的意义和作用.
3.理解集中趋势参数的统计含义.
4.培养直观想象、数学建模和数学运算素养.
自主预习·新知导学
合作探究·释疑解惑
随
堂
练
习
自主预习·新知导学
平均数、中位数、众数
【问题思考】
1.在初中我们已经学均数、中位数、众数的知识,利用已有知识,回答下列问题:
(1)如果5个数x1,x2,x3,x4,x5的平均数为7,那么x1+1,x2+1,x3+1,
x4+1,x5+1这5个数的平均数是多少?
(2)一组数据12,15,24,25,31,31,31,36,36,37,39,44,49,50的中位数是多少?众数是多少?
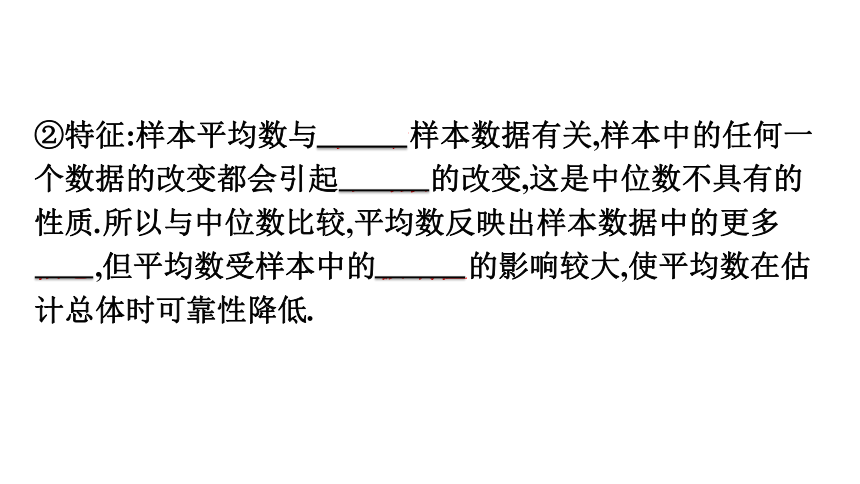
②特征:样本平均数与每一个样本数据有关,样本中的任何一个数据的改变都会引起平均数的改变,这是中位数不具有的性质.所以与中位数比较,平均数反映出样本数据中的更多
信息,但平均数受样本中的极端值的影响较大,使平均数在估计总体时可靠性降低.
(2)中位数
①定义:一组数据按从小到大的顺序排成一列,处于中间位置的数称为这组数据的中位数.在频率分布直方图中,中位数左边和右边的直方图的面积相等.
②特征:一组数据的中位数是唯一的,中位数只利用了样本数据中间位置的一个或两个值,并未利用其他数据,所以不是任何一个样本数据的改变都会引起中位数的改变.
(3)众数
①定义:一组数据中出现次数最多的数称为这组数据的众数.在频率分布直方图中,众数是最高矩形的底边的中点.
②特征:一组数据中的众数可能不止一个.众数只能告诉我们它比其他值出现的次数多,但并未告诉我们它比别的数值多的程度.因此,众数只能传递数据中的信息的很少一部分,对极端值也不敏感.
(4)一般地,对数值型数据(如用水量、身高、收入、产量等)集中趋势的描述,可以用平均数、中位数;而对分类型数据(如校服规格、性别、产品质量等级等)集中趋势的描述,可以用众数.
(5)平均数和中位数都描述了数据的集中趋势,它们的大小关系和数据分布的形态有关.
一般来说,对一个单峰的频率分布直方图来说,如果直方图的形状是对称的,那么平均数和中位数应该大体上差不多;如果直方图在右边“拖尾”,那么平均数大于中位数;如果直方图在左边“拖尾”,那么平均数小于中位数.也就是说,和中位数相比,平均数总是在“长尾巴”那边.
3.做一做:
(1)一个样本数据如下:5.3,5.2,5.1,5,3.3,4,4.5,3.2,4.5,则该样本的众数和中位数分别为( )
A.4.5和5
B.4.5和4
C.4.5和4.5
D.4.5和4.75
(2)已知一组观察值4,3,5,6出现的次数分别为3,2,4,2,则样本平均值为( )
A.4.55
B.4.5
C.12.5
D.1.64
解析:(1)将样本数据按从小到大的顺序排列:
3.2,3.3,4,4.5,4.5,5,5.1,5.2,5.3,
故众数为4.5,中位数为4.5.
答案:(1)C (2)A
【思考辨析】
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)若数据个数为偶数,则中位数是按从小到大顺序排列的最中间的那两个数.(
×
)
(2)在频率分布直方图中,众数是最高矩形的底边的中点.(
√
)
(3)因为样本平均数与每一个样本数据有关,所以用平均数能更好地反映数据的集中趋势.(
×
)
(4)在一组数据中,众数只有一个.(
×
)
合作探究·释疑解惑
探究一
探究二
探究三
探究一
平均数、中位数、众数在具体数据中的应用
【例1】
高一(3)班有男同学27名,女同学21名,在一次语文测验中,男同学的平均分是82分,中位数是75分,女同学的平均分是80分,中位数是80分.
(1)求这次测验全班的平均分(精确到0.01分);
(2)估计全班成绩在80分以下(含80分)的同学至少有多少人;
(3)分析男同学的平均分与中位数相差较大的主要原因.
分析:根据平均数和中位数的定义解决.
(2)因为男同学成绩的中位数是75分,
所以至少有14人得分不超过75分.
又因为女同学成绩的中位数是80分,
所以至少有11人得分不超过80分.
所以估计全班至少有25人得分低于80分(含80分).
(3)男同学的平均分与中位数的差别较大,说明男同学的成绩中两极分化现象严重,分数高的和低的相差较大.
若样本平均数大于样本中位数,则说明数据中存在许多较大的极端值;反之,说明数据中存在许多较小的极端值.中位数、平均数都是描述数值型数据的集中趋势的量,其中样本平均数的大小与每一个样本数据有关,任何一个数据的改变都会引起平均数的改变;但中位数只利用了样本数据中间位置的一个或两个值,并未利用其他数据,所以不是任何一个样本数据的改变都会引起中位数的改变.
【变式训练1】
某工厂人员及周工资构成如下表:
(1)求工厂人员周工资的众数、中位数、平均数;
(2)平均数能客观地反映该工厂的工资水平吗?为什么?
解:(1)由题中表格可知,众数为1
200,中位数为1
220,平均数为(2
200+1
250×6+1
220×5+1
200×10+490)÷23=1
230.
(2)虽然平均数为1
230元/周,但从题干表格中所列出的数据可见,只有经理和6名管理人员的周工资在平均数以上,其余17人的周工资都在平均数以下,故用平均数不能客观真实地反映该厂的工资水平.
探究二
在频率分布直方图中求平均数、中位数、众数
【例2】
某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.
?
(1)求这次测试数学成绩的众数;
(2)求这次测试数学成绩的中位数;
(3)求这次测试数学成绩的平均分.
分析:利用频率分布直方图求众数、中位数、平均数,众数、中位数分别是频率分布直方图中最高的小矩形的中间值、累计频率为0.5时所对应的样本数据的值,平均数可以用每个小矩形底边中点的横坐标与小矩形的面积的乘积之和近似代替.
本例条件不变,试估计80分以上的学生人数.
解:[80,90)分的频率为0.025×10=0.25,
频数为0.25×80=20.
[90,100)分的频率为0.005×10=0.05,
频数为0.05×80=4.
所以估计80分以上的学生人数为20+4=24.
1.众数、中位数、平均数与频率分布表、频率分布直方图的关系
(1)众数:众数一般用频率分布表中频率最高的一小组的组中值来表示,即在样本数据的频率分布直方图中,最高矩形的底边中点的横坐标.
(2)中位数:在频率分布表中,中位数是累计频率(样本数据小于某一数值的频率叫作该数值点的累计频率)为0.5时所对应的样本数据的值,而在样本中有50%的个体小于或等于中位数,也有50%的个体大于或等于中位数.因此,在频率分布直方图中,中位数左边和右边的直方图的面积应该相等.
(3)平均数:平均数在频率分布直方图中可以用每个小矩形底边中点的横坐标与小矩形的面积的乘积之和近似代替.平均数是频率分布直方图的“重心”.
2.利用直方图求众数、中位数、平均数均为近似值,往往与实际数据得出的不一致,但它们能粗略估计其众数、中位数和平均数.
【变式训练2】
某中学举行电脑知识竞赛,现将高一参赛学生的成绩整理后分成五组,绘制成频率分布直方图如图所示.已知图中从左到右的第一、二、三、四、五小组的频率分别是0.30,0.40,0.15,0.10,0.05.
求:(1)高一参赛学生的成绩的众数、中位数;
(2)高一参赛学生的平均成绩.
解:(1)由题图可知众数为65.
因为第一个小矩形的面积为0.3,
第二个小矩形的面积为0.4,0.3+0.4>0.5,因此中位数位于第二个小矩形内.
所以设中位数为60+x,
则0.3+x×0.04=0.5,得x=5,
所以中位数为60+5=65.
(2)依题意,平均成绩为55×0.3+65×0.4+75×0.15+85×0.1+95×0.05=67,
故平均成绩约为67.
随
堂
练
习
1.奥运会体操比赛的计分规则为:当评委亮分后,其成绩先去掉一个最高分,去掉一个最低分,再计算剩下分数的平均值,这是因为( )
A.减少计算量
B.避免故障
C.剔除异常值
D.活跃赛场气氛
解析:因为在体操比赛的评分中使用的是平均分,所以计分过程中采用“去掉一个最高分,去掉一个最低分”的方法,防止个别裁判的人为因素给出过高或过低的分数对选手的得分造成较大的影响,从而降低误差,尽量公平.
答案:C
2.已知一组数据为20,30,40,50,50,60,70,80.其中平均数、中位数和众数的大小关系是( )
A.平均数>中位数>众数
B.平均数<中位数<众数
C.中位数<众数<平均数
D.众数=中位数=平均数
答案:D
3.某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,则由此求出的平均数与实际平均数的差是
( )
A.3.5
B.-3
C.3
D.-0.5
答案:B
4.若已知某组数据的频率分布直方图如图所示,则估计该组数据的众数为 ,中位数为 .?
解析:由于众数是样本中出现次数最多的数,由直方图可估计为15.5.中位数是样本中的中间数据,由于样本数据在区间[13,14)的频率为0.02,在区间[14,15)内的频率为0.18,在区间[15,16)内的频率为0.36,0.02+0.18+0.36>0.5,所以中位数落在区间[15,16)内,设中位数为x,
5.某水厂为了了解某小区居民的用水情况,随机抽查了该小区10户家庭的月用水量,结果如下:
(1)计算这10户家庭该月平均用水量;
(2)如果该小区有500户家庭,根据上面的计算结果,估计该小区居民每月共用水多少立方米?
课标定位
素养阐释
1.结合实例,能用样本估计总体的集中趋势参数(平均数、中位数、众数).
2.会求样本数据的平均数、中位数、众数并理解它们的意义和作用.
3.理解集中趋势参数的统计含义.
4.培养直观想象、数学建模和数学运算素养.
自主预习·新知导学
合作探究·释疑解惑
随
堂
练
习
自主预习·新知导学
平均数、中位数、众数
【问题思考】
1.在初中我们已经学均数、中位数、众数的知识,利用已有知识,回答下列问题:
(1)如果5个数x1,x2,x3,x4,x5的平均数为7,那么x1+1,x2+1,x3+1,
x4+1,x5+1这5个数的平均数是多少?
(2)一组数据12,15,24,25,31,31,31,36,36,37,39,44,49,50的中位数是多少?众数是多少?
②特征:样本平均数与每一个样本数据有关,样本中的任何一个数据的改变都会引起平均数的改变,这是中位数不具有的性质.所以与中位数比较,平均数反映出样本数据中的更多
信息,但平均数受样本中的极端值的影响较大,使平均数在估计总体时可靠性降低.
(2)中位数
①定义:一组数据按从小到大的顺序排成一列,处于中间位置的数称为这组数据的中位数.在频率分布直方图中,中位数左边和右边的直方图的面积相等.
②特征:一组数据的中位数是唯一的,中位数只利用了样本数据中间位置的一个或两个值,并未利用其他数据,所以不是任何一个样本数据的改变都会引起中位数的改变.
(3)众数
①定义:一组数据中出现次数最多的数称为这组数据的众数.在频率分布直方图中,众数是最高矩形的底边的中点.
②特征:一组数据中的众数可能不止一个.众数只能告诉我们它比其他值出现的次数多,但并未告诉我们它比别的数值多的程度.因此,众数只能传递数据中的信息的很少一部分,对极端值也不敏感.
(4)一般地,对数值型数据(如用水量、身高、收入、产量等)集中趋势的描述,可以用平均数、中位数;而对分类型数据(如校服规格、性别、产品质量等级等)集中趋势的描述,可以用众数.
(5)平均数和中位数都描述了数据的集中趋势,它们的大小关系和数据分布的形态有关.
一般来说,对一个单峰的频率分布直方图来说,如果直方图的形状是对称的,那么平均数和中位数应该大体上差不多;如果直方图在右边“拖尾”,那么平均数大于中位数;如果直方图在左边“拖尾”,那么平均数小于中位数.也就是说,和中位数相比,平均数总是在“长尾巴”那边.
3.做一做:
(1)一个样本数据如下:5.3,5.2,5.1,5,3.3,4,4.5,3.2,4.5,则该样本的众数和中位数分别为( )
A.4.5和5
B.4.5和4
C.4.5和4.5
D.4.5和4.75
(2)已知一组观察值4,3,5,6出现的次数分别为3,2,4,2,则样本平均值为( )
A.4.55
B.4.5
C.12.5
D.1.64
解析:(1)将样本数据按从小到大的顺序排列:
3.2,3.3,4,4.5,4.5,5,5.1,5.2,5.3,
故众数为4.5,中位数为4.5.
答案:(1)C (2)A
【思考辨析】
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)若数据个数为偶数,则中位数是按从小到大顺序排列的最中间的那两个数.(
×
)
(2)在频率分布直方图中,众数是最高矩形的底边的中点.(
√
)
(3)因为样本平均数与每一个样本数据有关,所以用平均数能更好地反映数据的集中趋势.(
×
)
(4)在一组数据中,众数只有一个.(
×
)
合作探究·释疑解惑
探究一
探究二
探究三
探究一
平均数、中位数、众数在具体数据中的应用
【例1】
高一(3)班有男同学27名,女同学21名,在一次语文测验中,男同学的平均分是82分,中位数是75分,女同学的平均分是80分,中位数是80分.
(1)求这次测验全班的平均分(精确到0.01分);
(2)估计全班成绩在80分以下(含80分)的同学至少有多少人;
(3)分析男同学的平均分与中位数相差较大的主要原因.
分析:根据平均数和中位数的定义解决.
(2)因为男同学成绩的中位数是75分,
所以至少有14人得分不超过75分.
又因为女同学成绩的中位数是80分,
所以至少有11人得分不超过80分.
所以估计全班至少有25人得分低于80分(含80分).
(3)男同学的平均分与中位数的差别较大,说明男同学的成绩中两极分化现象严重,分数高的和低的相差较大.
若样本平均数大于样本中位数,则说明数据中存在许多较大的极端值;反之,说明数据中存在许多较小的极端值.中位数、平均数都是描述数值型数据的集中趋势的量,其中样本平均数的大小与每一个样本数据有关,任何一个数据的改变都会引起平均数的改变;但中位数只利用了样本数据中间位置的一个或两个值,并未利用其他数据,所以不是任何一个样本数据的改变都会引起中位数的改变.
【变式训练1】
某工厂人员及周工资构成如下表:
(1)求工厂人员周工资的众数、中位数、平均数;
(2)平均数能客观地反映该工厂的工资水平吗?为什么?
解:(1)由题中表格可知,众数为1
200,中位数为1
220,平均数为(2
200+1
250×6+1
220×5+1
200×10+490)÷23=1
230.
(2)虽然平均数为1
230元/周,但从题干表格中所列出的数据可见,只有经理和6名管理人员的周工资在平均数以上,其余17人的周工资都在平均数以下,故用平均数不能客观真实地反映该厂的工资水平.
探究二
在频率分布直方图中求平均数、中位数、众数
【例2】
某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.
?
(1)求这次测试数学成绩的众数;
(2)求这次测试数学成绩的中位数;
(3)求这次测试数学成绩的平均分.
分析:利用频率分布直方图求众数、中位数、平均数,众数、中位数分别是频率分布直方图中最高的小矩形的中间值、累计频率为0.5时所对应的样本数据的值,平均数可以用每个小矩形底边中点的横坐标与小矩形的面积的乘积之和近似代替.
本例条件不变,试估计80分以上的学生人数.
解:[80,90)分的频率为0.025×10=0.25,
频数为0.25×80=20.
[90,100)分的频率为0.005×10=0.05,
频数为0.05×80=4.
所以估计80分以上的学生人数为20+4=24.
1.众数、中位数、平均数与频率分布表、频率分布直方图的关系
(1)众数:众数一般用频率分布表中频率最高的一小组的组中值来表示,即在样本数据的频率分布直方图中,最高矩形的底边中点的横坐标.
(2)中位数:在频率分布表中,中位数是累计频率(样本数据小于某一数值的频率叫作该数值点的累计频率)为0.5时所对应的样本数据的值,而在样本中有50%的个体小于或等于中位数,也有50%的个体大于或等于中位数.因此,在频率分布直方图中,中位数左边和右边的直方图的面积应该相等.
(3)平均数:平均数在频率分布直方图中可以用每个小矩形底边中点的横坐标与小矩形的面积的乘积之和近似代替.平均数是频率分布直方图的“重心”.
2.利用直方图求众数、中位数、平均数均为近似值,往往与实际数据得出的不一致,但它们能粗略估计其众数、中位数和平均数.
【变式训练2】
某中学举行电脑知识竞赛,现将高一参赛学生的成绩整理后分成五组,绘制成频率分布直方图如图所示.已知图中从左到右的第一、二、三、四、五小组的频率分别是0.30,0.40,0.15,0.10,0.05.
求:(1)高一参赛学生的成绩的众数、中位数;
(2)高一参赛学生的平均成绩.
解:(1)由题图可知众数为65.
因为第一个小矩形的面积为0.3,
第二个小矩形的面积为0.4,0.3+0.4>0.5,因此中位数位于第二个小矩形内.
所以设中位数为60+x,
则0.3+x×0.04=0.5,得x=5,
所以中位数为60+5=65.
(2)依题意,平均成绩为55×0.3+65×0.4+75×0.15+85×0.1+95×0.05=67,
故平均成绩约为67.
随
堂
练
习
1.奥运会体操比赛的计分规则为:当评委亮分后,其成绩先去掉一个最高分,去掉一个最低分,再计算剩下分数的平均值,这是因为( )
A.减少计算量
B.避免故障
C.剔除异常值
D.活跃赛场气氛
解析:因为在体操比赛的评分中使用的是平均分,所以计分过程中采用“去掉一个最高分,去掉一个最低分”的方法,防止个别裁判的人为因素给出过高或过低的分数对选手的得分造成较大的影响,从而降低误差,尽量公平.
答案:C
2.已知一组数据为20,30,40,50,50,60,70,80.其中平均数、中位数和众数的大小关系是( )
A.平均数>中位数>众数
B.平均数<中位数<众数
C.中位数<众数<平均数
D.众数=中位数=平均数
答案:D
3.某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,则由此求出的平均数与实际平均数的差是
( )
A.3.5
B.-3
C.3
D.-0.5
答案:B
4.若已知某组数据的频率分布直方图如图所示,则估计该组数据的众数为 ,中位数为 .?
解析:由于众数是样本中出现次数最多的数,由直方图可估计为15.5.中位数是样本中的中间数据,由于样本数据在区间[13,14)的频率为0.02,在区间[14,15)内的频率为0.18,在区间[15,16)内的频率为0.36,0.02+0.18+0.36>0.5,所以中位数落在区间[15,16)内,设中位数为x,
5.某水厂为了了解某小区居民的用水情况,随机抽查了该小区10户家庭的月用水量,结果如下:
(1)计算这10户家庭该月平均用水量;
(2)如果该小区有500户家庭,根据上面的计算结果,估计该小区居民每月共用水多少立方米?
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
