6.1分类加法原理和分步乘法原理 同步训练A-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(含解析)
文档属性
| 名称 | 6.1分类加法原理和分步乘法原理 同步训练A-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-13 21:35:10 | ||
图片预览


文档简介
6.1分类加法原理和分步乘法原理A
一.选择题(共10小题)
1.如图,湖面上有4个相邻的小岛,,,,现要建3座桥梁,将这4个小岛连接起来共有种不同的方案,则的值为
A.4 B.8 C.12 D.16
2.从4种不同的书中买3本送给3名同学,每人各1本,不同的送法共有
A.4种 B.12种 C.24种 D.64种
3.电路如图所示,在,间有四个开关,若发现,之间电路不通,则这四个开关打开或闭合的方式有
A.3种 B.8种 C.13种 D.16种
4.从地到地要经过地,已知从地到地有三条路,从地到地有四条路,则从地到地不同的走法种数是
A.7 B.9 C.12 D.16
5.高二年级要从3名男生,2名女生中选派3人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案有
A.6种 B.7种 C.8种 D.9种
6.某班联欢会原定的3个节目已排成节目单,开演前又增加了2个新节目,如果将这2个新节目插入节目单中,那么不同的插法种数为
A.12 B.20 C.36 D.120
7.中国足球队超级联赛的积分规则是:胜一场得3分,平一场得1分,负一场得0分.某球队打完3场比赛,则该球队积分情况共有几 种.
A.8 B.9 C.10 D.11
8.一只蚂蚁从正四面体的顶点出发,沿着正四面体的棱爬行,每秒爬一条棱,每次爬行的方向是随机的,则蚂蚁第1秒后到点,第4秒后又回到点的不同爬行路线有
A.6条 B.7条 C.8条 D.9条
9.如图,从甲地到乙地有3条路,从乙地到丁地有2条路;从甲地到丙地有3条路,从丙地到丁地有4条路.从甲地到丁地的不同路线共有
A.12条 B.15条 C.18条 D.72条
二.填空题(共4小题)
10.若,2,,则集合,共有 种组合.
11.已知集合,2,3,4,,若,是的两个非空子集,则所有满足中的最大数小于中的最小数的集合对的个数为 .
12.北京大兴国际机场为级国际机场、大型国际枢纽机场、国家发展新动力源,于2019年9月25日正式通航.目前建有“三纵一横”4条跑道,分别叫西一跑道、西二跑道、东一跑道、北一跑道,如图所示;若有2架飞往不同目的地的飞机要从以上不同跑道同时起飞,且西一跑道、西二跑道至少有一道被选取,则共有 种不同的安排方法.(用数字作答).
13.设为一个非空有限集合,记为集合中元素的个数,若集合的两个子集、满足:并且,则称子集,为集合的一个“覆盖”(其中,若,则的“覆盖”个数为 .
三.解答题(共4小题)
14.某校从6名教师中,选派4名同时到3个边远地区支教,每个地区至少选派1名.
(1)共有多少种不同的选派方法?
(2)若6名教师中的甲、乙二位教师不能同时支教,共有多少种不同的选派方法?
15.生产过程有4道工序,每道工序需要安排一人照看,现从甲、乙、丙等6名工人中安排4人分别照看一道工序,第一道工序安排乙做,第四道工序只能从甲、丙两人中安排1人,则不同的安排方案有多少种?
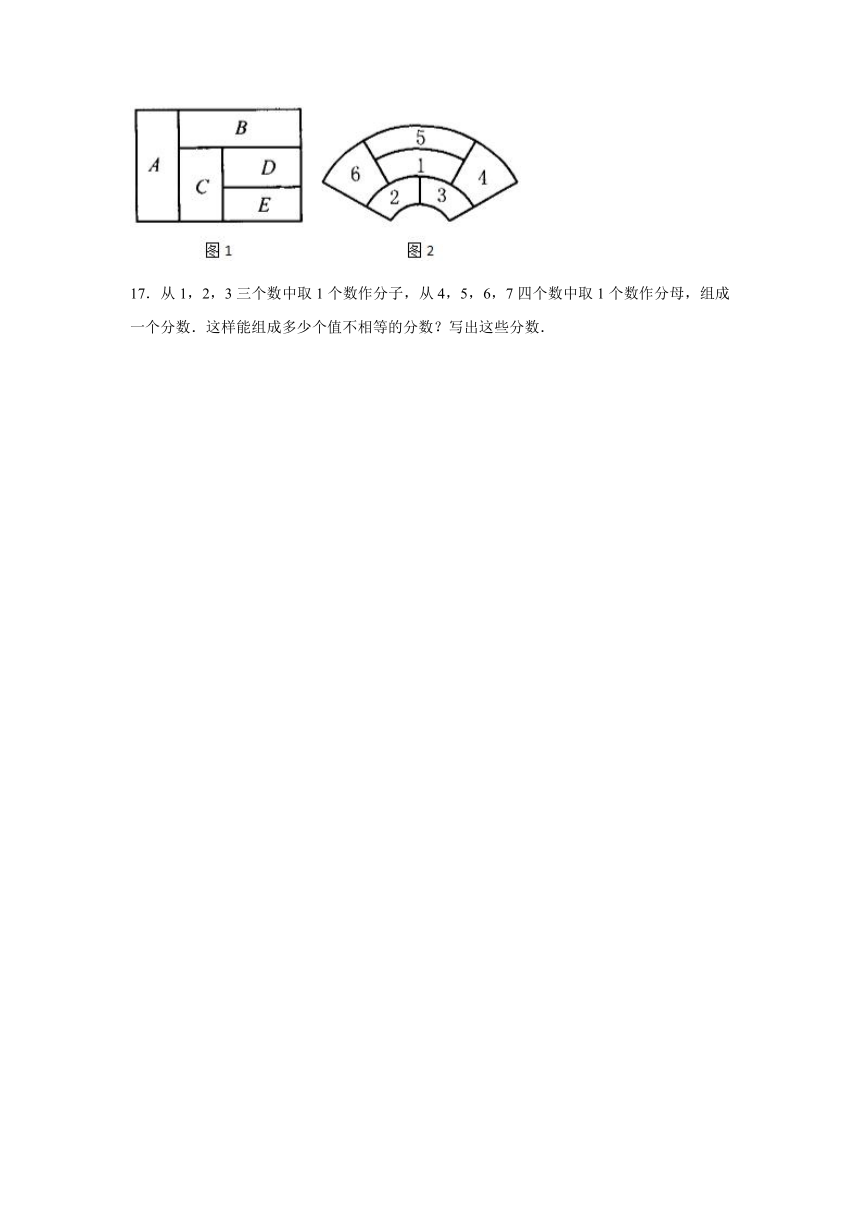
16.用5种不同的颜色分别给图1、图2的各部分着色.相邻部分不能用同一种颜色,但同一种颜色可以反复使用,也可不使用.分别求出各图中符合条件的着色方法的种数.
17.从1,2,3三个数中取1个数作分子,从4,5,6,7四个数中取1个数作分母,组成一个分数.这样能组成多少个值不相等的分数?写出这些分数.
6.1分类加法原理和分步乘法原理A
参考答案与试题解析
一.选择题(共10小题)
1.【解答】解:根据题意,4个小岛之间共有6个位置可以建设桥梁,在其中任选3个建造桥梁,有种结果,
其中有4种不能把4个小岛连接起来,则符合题意的建造方法有种;
故选:.
2.【解答】解:根据题意,从4种不同的书中买3本送给3名同学,每人各1本,不同的送法共有种.
故选:.
3.【解答】解:根据题意,在,间有四个开关,每个开关有2种情况,则四个开关有种情况,
其中电路接通的情况有1、2、4闭合、1、3、4闭合或1、2、3、4闭合,有3种情况,
则电路不通的情况有种;
故选:.
4.【解答】解:根据题意,从地到地要经过地,已知从地到地有三条路,则从到有3种不同的走法,
从地到地有四条路,则从到有4种不同的走法,
则从地到地不同的走法种数有种;
故选:.
5.【解答】解:方法一:可按女生人数分类:
若选派1名女生,有种;
若选派2名女生,则有种.
由分类加法计数原理,共有9种不同的选派方法.
方法二:至少有1名女生的选派方法为.
故选:.
6.【解答】解:利用分步计数原理,第一步先插入第一个节目,有4种方法,第二步插入第二个节目,此时有5个空,故有5种方法.因此不同的插法共有20种.
故选:.
7.【解答】解:打完3场比赛,可能出现的胜负情况为:三胜,二胜一平,二胜一负,一胜二平,一胜二负,一胜一平一负;三平,二平一负,一平二负;三负;
对应的积分依次为:9,7,6,5,3,4,3,2,1,0;共9种积分情况.
故选:.
8.【解答】解:根据已知,可作出右图,
由图知,不同的爬行路线有7条,
故选:.
9.【解答】解:分两类,第一类,从甲到乙再到丁,共有种,
第二类,从甲到丙再到丁,共有种,
根据分类计数原理可得,共有种,
故从甲地到丁地共有18条不同的路线.
故选:.
二.填空题(共4小题)
10.【解答】解:当集合为空集时,集合,2,有1种,
当集合包含1个元素时,例如,则集合可以为,2,或,,故有种,
当集合包含2个元素时,例如,,则可以为,2,,,,,,故有种,
当集合包含3个元素时,例如,2,,则集合可以没有元素,1个元素,2个元素,3个元素,故有种,
根据分类计数原理可得,共有种,
故答案为:27.
11.【解答】解:根据题意,分4种情况讨论:
当中的最大数为1,即时,,,,,,,,,,,,,,,,,,3,,,3,,,4,,,4,,,3,4,,即,3,4,的非空子集的个数为个;
当中的最大数为2,即,,时,,,,,,,,,,,4,,即个;
当中的最大数为3,即,,,,,,2,时,,,,,即个;
当中的最大数为4,即,,,,,,,,2,,,3,,,3,,,2,3,时,,即,2,的子集的个数为个;
所以总共个数为个;
故答案为:49.
12.【解答】解:①西一跑道、西二跑道均被选取,有种起飞方式;
②西一跑道、西二跑道只有一道被选取,有种起飞方式;
由分类计数原理可知,满足条件的安排方法有种.
故答案为:10.
13.【解答】解:根据题意,分2步进行分析:
①若,即集合中有个元素,在其中任选个,有种取法,
②集合中还有个元素,假设这个元素组成集合,集合有个子集,
则的“覆盖”个数为;
故答案为:
三.解答题(共4小题)
14.【解答】解:(1)选派4名同时到3个边远地区支教,每个地区至少选派1名,则有一地区有2人,其余1人,
从6名教师中,选派4名,再从4名中选2人,再分配到三个地区,故有种,
(2)第一类,不选甲乙,故有种,
第二类,选甲乙中的一人,故有种,
根据分类计数原理得,共有种
15.【解答】解:由题意,第一道工序安排乙做,第四道工序只能从甲、丙两人中安排1人,
故完成方案共有种.
16.【解答】解:根据题意,对于图1,先涂,则有5种涂法,再涂,因为与相邻,所以的颜色只要与不同即可,有4种涂法,
同理有3种涂法,有3种涂法,有3种涂法,
由分步乘法计数原理可知,复合这些要求的不同着色的方法共有为种,
对于图2,两两不相邻部分的有2和4、2和5、3和5、3和6、4和6,
分2种情况讨论:
①用5种颜色着色,需要在5个不相邻的区域中,任选1个,涂同一种颜色,此时有种着色方案,
②用4种颜色着色,先在5种颜色中任选4种,有种选法,
再在5个不相邻的区域中选1对,涂同一种颜色,有“2和4、3和5”、“2和4、2和6”、“2和5、3和6”、“2和5、4和6”、“3和5、4和6”,共5种情况,
最后将4种颜色填在4个区域,则有种着色方案,
则共有种着色方案.
17.【解答】解:从1,2,3三个数中取1个数作分子,从4,5,6,7四个数中取1个数作分母,组成的分数个数为,
其中,所以组成值不相等的分数个数为.
它们是,,,,,,,,,,.
一.选择题(共10小题)
1.如图,湖面上有4个相邻的小岛,,,,现要建3座桥梁,将这4个小岛连接起来共有种不同的方案,则的值为
A.4 B.8 C.12 D.16
2.从4种不同的书中买3本送给3名同学,每人各1本,不同的送法共有
A.4种 B.12种 C.24种 D.64种
3.电路如图所示,在,间有四个开关,若发现,之间电路不通,则这四个开关打开或闭合的方式有
A.3种 B.8种 C.13种 D.16种
4.从地到地要经过地,已知从地到地有三条路,从地到地有四条路,则从地到地不同的走法种数是
A.7 B.9 C.12 D.16
5.高二年级要从3名男生,2名女生中选派3人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案有
A.6种 B.7种 C.8种 D.9种
6.某班联欢会原定的3个节目已排成节目单,开演前又增加了2个新节目,如果将这2个新节目插入节目单中,那么不同的插法种数为
A.12 B.20 C.36 D.120
7.中国足球队超级联赛的积分规则是:胜一场得3分,平一场得1分,负一场得0分.某球队打完3场比赛,则该球队积分情况共有几 种.
A.8 B.9 C.10 D.11
8.一只蚂蚁从正四面体的顶点出发,沿着正四面体的棱爬行,每秒爬一条棱,每次爬行的方向是随机的,则蚂蚁第1秒后到点,第4秒后又回到点的不同爬行路线有
A.6条 B.7条 C.8条 D.9条
9.如图,从甲地到乙地有3条路,从乙地到丁地有2条路;从甲地到丙地有3条路,从丙地到丁地有4条路.从甲地到丁地的不同路线共有
A.12条 B.15条 C.18条 D.72条
二.填空题(共4小题)
10.若,2,,则集合,共有 种组合.
11.已知集合,2,3,4,,若,是的两个非空子集,则所有满足中的最大数小于中的最小数的集合对的个数为 .
12.北京大兴国际机场为级国际机场、大型国际枢纽机场、国家发展新动力源,于2019年9月25日正式通航.目前建有“三纵一横”4条跑道,分别叫西一跑道、西二跑道、东一跑道、北一跑道,如图所示;若有2架飞往不同目的地的飞机要从以上不同跑道同时起飞,且西一跑道、西二跑道至少有一道被选取,则共有 种不同的安排方法.(用数字作答).
13.设为一个非空有限集合,记为集合中元素的个数,若集合的两个子集、满足:并且,则称子集,为集合的一个“覆盖”(其中,若,则的“覆盖”个数为 .
三.解答题(共4小题)
14.某校从6名教师中,选派4名同时到3个边远地区支教,每个地区至少选派1名.
(1)共有多少种不同的选派方法?
(2)若6名教师中的甲、乙二位教师不能同时支教,共有多少种不同的选派方法?
15.生产过程有4道工序,每道工序需要安排一人照看,现从甲、乙、丙等6名工人中安排4人分别照看一道工序,第一道工序安排乙做,第四道工序只能从甲、丙两人中安排1人,则不同的安排方案有多少种?
16.用5种不同的颜色分别给图1、图2的各部分着色.相邻部分不能用同一种颜色,但同一种颜色可以反复使用,也可不使用.分别求出各图中符合条件的着色方法的种数.
17.从1,2,3三个数中取1个数作分子,从4,5,6,7四个数中取1个数作分母,组成一个分数.这样能组成多少个值不相等的分数?写出这些分数.
6.1分类加法原理和分步乘法原理A
参考答案与试题解析
一.选择题(共10小题)
1.【解答】解:根据题意,4个小岛之间共有6个位置可以建设桥梁,在其中任选3个建造桥梁,有种结果,
其中有4种不能把4个小岛连接起来,则符合题意的建造方法有种;
故选:.
2.【解答】解:根据题意,从4种不同的书中买3本送给3名同学,每人各1本,不同的送法共有种.
故选:.
3.【解答】解:根据题意,在,间有四个开关,每个开关有2种情况,则四个开关有种情况,
其中电路接通的情况有1、2、4闭合、1、3、4闭合或1、2、3、4闭合,有3种情况,
则电路不通的情况有种;
故选:.
4.【解答】解:根据题意,从地到地要经过地,已知从地到地有三条路,则从到有3种不同的走法,
从地到地有四条路,则从到有4种不同的走法,
则从地到地不同的走法种数有种;
故选:.
5.【解答】解:方法一:可按女生人数分类:
若选派1名女生,有种;
若选派2名女生,则有种.
由分类加法计数原理,共有9种不同的选派方法.
方法二:至少有1名女生的选派方法为.
故选:.
6.【解答】解:利用分步计数原理,第一步先插入第一个节目,有4种方法,第二步插入第二个节目,此时有5个空,故有5种方法.因此不同的插法共有20种.
故选:.
7.【解答】解:打完3场比赛,可能出现的胜负情况为:三胜,二胜一平,二胜一负,一胜二平,一胜二负,一胜一平一负;三平,二平一负,一平二负;三负;
对应的积分依次为:9,7,6,5,3,4,3,2,1,0;共9种积分情况.
故选:.
8.【解答】解:根据已知,可作出右图,
由图知,不同的爬行路线有7条,
故选:.
9.【解答】解:分两类,第一类,从甲到乙再到丁,共有种,
第二类,从甲到丙再到丁,共有种,
根据分类计数原理可得,共有种,
故从甲地到丁地共有18条不同的路线.
故选:.
二.填空题(共4小题)
10.【解答】解:当集合为空集时,集合,2,有1种,
当集合包含1个元素时,例如,则集合可以为,2,或,,故有种,
当集合包含2个元素时,例如,,则可以为,2,,,,,,故有种,
当集合包含3个元素时,例如,2,,则集合可以没有元素,1个元素,2个元素,3个元素,故有种,
根据分类计数原理可得,共有种,
故答案为:27.
11.【解答】解:根据题意,分4种情况讨论:
当中的最大数为1,即时,,,,,,,,,,,,,,,,,,3,,,3,,,4,,,4,,,3,4,,即,3,4,的非空子集的个数为个;
当中的最大数为2,即,,时,,,,,,,,,,,4,,即个;
当中的最大数为3,即,,,,,,2,时,,,,,即个;
当中的最大数为4,即,,,,,,,,2,,,3,,,3,,,2,3,时,,即,2,的子集的个数为个;
所以总共个数为个;
故答案为:49.
12.【解答】解:①西一跑道、西二跑道均被选取,有种起飞方式;
②西一跑道、西二跑道只有一道被选取,有种起飞方式;
由分类计数原理可知,满足条件的安排方法有种.
故答案为:10.
13.【解答】解:根据题意,分2步进行分析:
①若,即集合中有个元素,在其中任选个,有种取法,
②集合中还有个元素,假设这个元素组成集合,集合有个子集,
则的“覆盖”个数为;
故答案为:
三.解答题(共4小题)
14.【解答】解:(1)选派4名同时到3个边远地区支教,每个地区至少选派1名,则有一地区有2人,其余1人,
从6名教师中,选派4名,再从4名中选2人,再分配到三个地区,故有种,
(2)第一类,不选甲乙,故有种,
第二类,选甲乙中的一人,故有种,
根据分类计数原理得,共有种
15.【解答】解:由题意,第一道工序安排乙做,第四道工序只能从甲、丙两人中安排1人,
故完成方案共有种.
16.【解答】解:根据题意,对于图1,先涂,则有5种涂法,再涂,因为与相邻,所以的颜色只要与不同即可,有4种涂法,
同理有3种涂法,有3种涂法,有3种涂法,
由分步乘法计数原理可知,复合这些要求的不同着色的方法共有为种,
对于图2,两两不相邻部分的有2和4、2和5、3和5、3和6、4和6,
分2种情况讨论:
①用5种颜色着色,需要在5个不相邻的区域中,任选1个,涂同一种颜色,此时有种着色方案,
②用4种颜色着色,先在5种颜色中任选4种,有种选法,
再在5个不相邻的区域中选1对,涂同一种颜色,有“2和4、3和5”、“2和4、2和6”、“2和5、3和6”、“2和5、4和6”、“3和5、4和6”,共5种情况,
最后将4种颜色填在4个区域,则有种着色方案,
则共有种着色方案.
17.【解答】解:从1,2,3三个数中取1个数作分子,从4,5,6,7四个数中取1个数作分母,组成的分数个数为,
其中,所以组成值不相等的分数个数为.
它们是,,,,,,,,,,.
