7.4宇宙航行 课件(共93张PPT)
文档属性
| 名称 | 7.4宇宙航行 课件(共93张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-12 00:00:00 | ||
图片预览










文档简介
(共93张PPT)
地面上抛出的物体,由于受到地球引力的作用,最终都要落回到地面。
1.月球也要受到地球引力的作用,为什么月亮不会落到地面上来?
一、牛顿关于卫星的设想
地面上抛出的物体,由于受到地球引力的作用,最终都要落回到地面。
1.月球也要受到地球引力的作用,为什么月亮不会落到地面上来?
由于月球在绕地球沿近似圆周的轨道运转,此时月球受到的地球引力,用来充当绕地球运转的向心力,故月球不会落到地面上来。
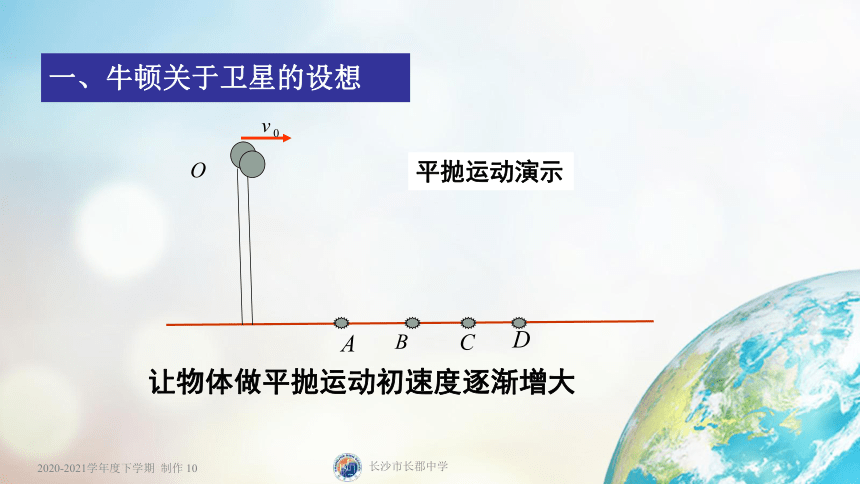
一、牛顿关于卫星的设想
平抛运动演示
让物体做平抛运动初速度逐渐增大
一、牛顿关于卫星的设想
从高山上水平抛出物体,速度越大,落地点离山脚越远。如果没有空气阻力,当速度足够大时,物体就永远不会落到地面上来,它将围绕地球旋转,成为一颗永远绕地球运动的人造卫星。
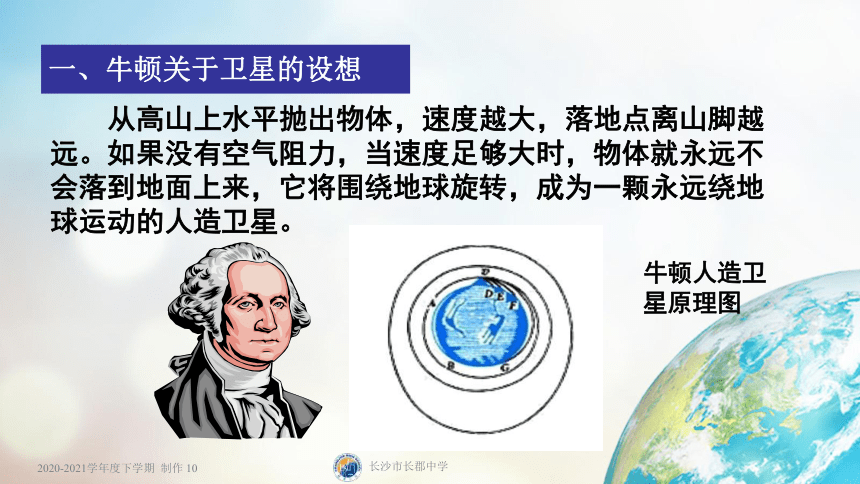
一、牛顿关于卫星的设想
牛顿人造卫星原理图
从高山上水平抛出物体,速度越大,落地点离山脚越远。如果没有空气阻力,当速度足够大时,物体就永远不会落到地面上来,它将围绕地球旋转,成为一颗永远绕地球运动的人造卫星。
一、牛顿关于卫星的设想
思考
以多大的速度将物体抛出,它才会成为绕地球表面运动的卫星?
二、宇宙速度
思考
以多大的速度将物体抛出,它才会成为绕地球表面运动的卫星?
方法一:万有引力提供物体作圆周运动的向心力
二、宇宙速度
思考
以多大的速度将物体抛出,它才会成为绕地球表面运动的卫星?
方法一:万有引力提供物体作圆周运动的向心力
方法二:地表附近,重力近似等于万有引力
二、宇宙速度
g=9.8m/s2,R=6400km,代入数据得:
由此可见:v=7.9km/s,这就是物体在地面附近绕地球做匀速圆周运动所必须具备的最小发射速度,称为:第一宇宙速度
二、宇宙速度
由此可见:v=7.9km/s,这就是物体在地面附近绕地球做匀速圆周运动所必须具备的最小发射速度,称为:第一宇宙速度
说明:
(1)
如果卫星的速度小于第一宇宙速度,卫星将落到地面而不能绕地球运转;
二、宇宙速度
由此可见:v=7.9km/s,这就是物体在地面附近绕地球做匀速圆周运动所必须具备的最小发射速度,称为:第一宇宙速度
说明:
(1)
如果卫星的速度小于第一宇宙速度,卫星将落到地面而不能绕地球运转;
(2)等于这个速度,卫星刚好能在地球表面附近作匀速圆周运动;
二、宇宙速度
P
v=7.9km/s
11.2>v>7.9
v>11.2km/s
探究:若卫星的发射速度大于7.9km/s
,会怎样呢?
1.
第一宇宙速度:
v1=7.9km/s
地球
11.2km/s>v>7.9km/s
2.
第二宇宙速度:
v2=11.2km/s
v3=16.7km/s
3.
第三宇宙速度:
→人造行星
→人造恒星
→人造卫星
例1.
某人在一星球上以速率
v
竖直上抛一物体,经时间
t
后,物体以速率
v
落回手中。已知该星球的半径为
R
,求该星球上的第一宇宙速度。
例1.
某人在一星球上以速率
v
竖直上抛一物体,经时间
t
后,物体以速率
v
落回手中。已知该星球的半径为
R
,求该星球上的第一宇宙速度。
解析:星球表面的重力加速度:
该星球表面的第一宇宙速度为
第一宇宙速度为卫星在其表面附近做匀速圆周运动的线速度卫星的重力提供向心力,则:
思考:将各种卫星绕地球运动都近似看成匀速圆周运动,你能推出卫星环绕速度、角速度、周期、向心加速度与轨道半径的关系吗?
1
2
4
3
人造卫星运行的动力学方程
三、人造地球卫星运行的规律
地球
思考:对于绕地球运动的人造卫星:
(1)离地面越高,向心力越_____.
(2)离地面越高,线速度越_____.
(3)离地面越高,周期越_____.
(4)离地面越高,角速度越____.
三、人造地球卫星运行的规律
地球
思考:对于绕地球运动的人造卫星:
(1)离地面越高,向心力越_____.
(2)离地面越高,线速度越_____.
(3)离地面越高,周期越_____.
(4)离地面越高,角速度越____.
小
三、人造地球卫星运行的规律
地球
思考:对于绕地球运动的人造卫星:
(1)离地面越高,向心力越_____.
(2)离地面越高,线速度越_____.
(3)离地面越高,周期越_____.
(4)离地面越高,角速度越____.
小
小
三、人造地球卫星运行的规律
地球
思考:对于绕地球运动的人造卫星:
(1)离地面越高,向心力越_____.
(2)离地面越高,线速度越_____.
(3)离地面越高,周期越_____.
(4)离地面越高,角速度越____.
小
大
小
三、人造地球卫星运行的规律
地球
思考:对于绕地球运动的人造卫星:
(1)离地面越高,向心力越_____.
(2)离地面越高,线速度越_____.
(3)离地面越高,周期越_____.
(4)离地面越高,角速度越____.
小
大
小
小
三、人造地球卫星运行的规律
地球
思考:对于绕地球运动的人造卫星:
(1)离地面越高,向心力越_____.
(2)离地面越高,线速度越_____.
(3)离地面越高,周期越_____.
(4)离地面越高,角速度越____.
小
大
小
小
第一宇宙速度是发射卫星的最小发射速度,也是卫星绕地球做圆周运动的最大运行速度.
三、人造地球卫星运行的规律
例2.
探测器绕月球做匀速圆周运动,变轨后在周期较小的轨道上仍做匀速圆周运动,则变轨后与变轨前相比(
)
A.
轨道半径变小
B.
向心加速度变小
C.
线速度变小
D.
角速度变小
例2.
探测器绕月球做匀速圆周运动,变轨后在周期较小的轨道上仍做匀速圆周运动,则变轨后与变轨前相比(
)
A.
轨道半径变小
B.
向心加速度变小
C.
线速度变小
D.
角速度变小
A
例3.
如图所示,a、b、c是地球大气层外圆形轨道上运行的三颗人造地球卫星,a、b质量相同,且小于c的质量,则(
)
A.
b所需向心力最大
B.
b、c周期相等,且大于a周期
C.
b、c向心加速度相等,且大于a的向心加速度
D.
b、c的线速度大小相等,且小于a的线速度
a
c
b
地球
例3.
如图所示,a、b、c是地球大气层外圆形轨道上运行的三颗人造地球卫星,a、b质量相同,且小于c的质量,则(
)
A.
b所需向心力最大
B.
b、c周期相等,且大于a周期
C.
b、c向心加速度相等,且大于a的向心加速度
D.
b、c的线速度大小相等,且小于a的线速度
BD
a
c
b
地球
各种各样的卫星……
四、人造地球卫星
赤道轨道
四、人造地球卫星
赤道轨道
极地轨道
四、人造地球卫星
赤道轨道
其它轨道
极地轨道
四、人造地球卫星
所有卫星都在以地心为圆心的圆或椭圆轨道上
三类人造地球卫星轨道:
①赤道轨道,卫星轨道在赤道平面,卫星始终处于赤道上方
②极地轨道,卫星轨道平面与赤道平面垂直,卫星通过两极上空
③一般轨道,卫星轨道和赤道成一定角度。
人造地球卫星的运行轨道
地球同步卫星
相对于地面静止的,和地球具有相同周期的卫星,T=24h,因为地球同步卫星主要用于通信等方面,故地球同步卫星又叫通信卫星
F1
F2
F3
h
若同步卫星离地面高度h
特点:
特点:
⑴定周期:T=24h=86400s
特点:
⑴定周期:T=24h=86400s
⑵定点:相对于地面静止。
特点:
⑴定周期:T=24h=86400s
⑵定点:相对于地面静止。
⑶定轨道:同步卫星轨道必须在赤道上空
特点:
⑴定周期:T=24h=86400s
⑵定点:相对于地面静止。
⑶定轨道:同步卫星轨道必须在赤道上空
⑷定高度:h=36000km
特点:
⑴定周期:T=24h=86400s
⑵定点:相对于地面静止。
⑶定轨道:同步卫星轨道必须在赤道上空
⑷定高度:h=36000km
⑸定速度:由于同步卫星高度确定,其轨道半径即确定,因此线速度、角速度大小均不变
特点:
⑴定周期:T=24h=86400s
⑵定点:相对于地面静止。
⑶定轨道:同步卫星轨道必须在赤道上空
⑷定高度:h=36000km
⑸定速度:由于同步卫星高度确定,其轨道半径即确定,因此线速度、角速度大小均不变
⑹定加速度:由于同步卫星高度确定,其轨道半径即确定,因此向心加速度大小也不变
四、人造地球卫星
同步卫星
近地卫星
月球
近地卫星、同步卫星、月球三者比较
h=3.8×108m
r≈3.8×108m
v=1km/s
T=27天
同步卫星
近地卫星
月球
近地卫星、同步卫星、月球三者比较
h=3.6×107m
r=4.2×107m
v=3km/s
T=24h
h=3.8×108m
r≈3.8×108m
v=1km/s
T=27天
同步卫星
近地卫星
月球
近地卫星、同步卫星、月球三者比较
h=3.6×107m
r=4.2×107m
v=3km/s
T=24h
h=3.8×108m
r≈3.8×108m
v=1km/s
T=27天
h≈0
r=6.4×106m
v=7.9km/s
T=84分钟
同步卫星
近地卫星
月球
近地卫星、同步卫星、月球三者比较
变轨
思考:人造卫星在低轨道上运行,要想让其在高轨道上运行,应采取什么措施?
v
F引
F引<F向
F引>F向
卫星变轨原理
M
m
A点速度—内小外大(在A点看轨迹)
在A点万有引力相同
A
v
F引
1
2
R
卫星在圆轨道运行速度V1
v2
θ>900
减小
卫星变轨原理
v3
F引
L
卫星变轨原理
使卫星进入更高轨道做圆周运动
v3
v4
·
1.
卫星在二轨道相切点
万有引力相同
速度—内小外大(切点看轨迹)
2.
卫星在椭圆轨道运行
近地点---速度大,动能大
远地点---速度小,动能小
1.
如图所示,发射同步卫星时,先将卫星发射至近地圆轨道1,然后经点火使其沿椭圆轨道2运行;最后再次点火将其送入同步圆轨道3。轨道1、2相切于P点,2、3相切于Q点。当卫星分别在1、2、3上正常运行时,以下说法正确的是(
)
A.
在轨道3上的速率大于1上的速率
B.
在轨道3上的角速度小于1上的角速度
C.
在轨道2上经过Q点时的速率等于
在轨道3上经过Q点时的速率
D.
在轨道1上经过P点时的加速度等于
在轨道2上经过P点时的加速度
Q
P
2
·
3
1
1.
如图所示,发射同步卫星时,先将卫星发射至近地圆轨道1,然后经点火使其沿椭圆轨道2运行;最后再次点火将其送入同步圆轨道3。轨道1、2相切于P点,2、3相切于Q点。当卫星分别在1、2、3上正常运行时,以下说法正确的是(
)
A.
在轨道3上的速率大于1上的速率
B.
在轨道3上的角速度小于1上的角速度
C.
在轨道2上经过Q点时的速率等于
在轨道3上经过Q点时的速率
D.
在轨道1上经过P点时的加速度等于
在轨道2上经过P点时的加速度
Q
P
2
·
3
1
BD
空间站实际上就是一个载有人的人造卫星,那么,地球上的人如何登到空间站,空间站上的人又如何返回地面?这些活动都需要通过宇宙飞船来完成,这就存在一个宇宙飞船与空间站对接的问题。
思考:能否把宇宙飞船先发射到空间站的同一轨道上,再通过加速去追上空间站实现对接呢?
宇宙飞船与空间站对接问题
空间站
飞船
对接方法:
飞船首先在比空间站低的轨道运行,当运行到适当位置时,再加速运行到一个椭圆轨道。
空间站
飞船
对接方法:
飞船首先在比空间站低的轨道运行,当运行到适当位置时,再加速运行到一个椭圆轨道。
通过控制轨道使飞船跟空间站恰好同时运行到两轨道的相切点,此时飞船适当减速,便可实现对接,如图示。
空间站
飞船
对接方法:
2.
宇宙飞船和轨道空间站在同一轨道上运动,若飞船想与前面的空间站对接,飞船为了追上轨道空间站,可采取的方法是:
(
)
A.
飞船加速直到追上
B.
飞船从原轨道减速至一个较低轨道,再加速追上空间站,完成对接
C.
飞船加速至一个较高轨道再减速追上空间站,完成对接
D.
无论飞船采取何种措施,均不能与空间站对接
2.
宇宙飞船和轨道空间站在同一轨道上运动,若飞船想与前面的空间站对接,飞船为了追上轨道空间站,可采取的方法是:
(
)
A.
飞船加速直到追上
B.
飞船从原轨道减速至一个较低轨道,再加速追上空间站,完成对接
C.
飞船加速至一个较高轨道再减速追上空间站,完成对接
D.
无论飞船采取何种措施,均不能与空间站对接
B
二、人造卫星的超重和失重
二、人造卫星的超重和失重
1.
发射和回收阶段
二、人造卫星的超重和失重
1.
发射和回收阶段
发射
加速上升
超重
二、人造卫星的超重和失重
1.
发射和回收阶段
发射
加速上升
超重
回收
减速下降
超重
二、人造卫星的超重和失重
1.
发射和回收阶段
发射
加速上升
超重
回收
减速下降
超重
2.
沿圆轨道正常运行
二、人造卫星的超重和失重
1.
发射和回收阶段
发射
加速上升
超重
回收
减速下降
超重
2.
沿圆轨道正常运行
只受重力
a
=
g
完全失重
二、人造卫星的超重和失重
1.
发射和回收阶段
发射
加速上升
超重
回收
减速下降
超重
2.
沿圆轨道正常运行
只受重力
a
=
g
完全失重
与重力有关的现象全部消失
二、人造卫星的超重和失重
1.
发射和回收阶段
发射
加速上升
超重
回收
减速下降
超重
2.
沿圆轨道正常运行
只受重力
a
=
g
完全失重
与重力有关的现象全部消失
天平
弹簧秤测重力
液体压强计
三、多星系统
1.
双星问题
(1)定义:绕公共圆心转动的两个星体组成的系统,我们称之为双星系统,如图所示.
(2)特点:
①各自所需的向心力由彼此间的万有引力相互提供,即
(2)特点:
①各自所需的向心力由彼此间的万有引力相互提供,即
②两颗星的周期及角速度都相同,即
T1=T2,ω1=ω2
(2)特点:
①各自所需的向心力由彼此间的万有引力相互提供,即
②两颗星的周期及角速度都相同,即
T1=T2,ω1=ω2
③两颗星的半径与它们之间的距离关系为:
r1+r2=L
1.
若在双星模型中,图中L、m1、m2、G为已知量,双星运动的周期如何表示?
2.
若双星运动的周期为T,双星之间的距离为L,G已知,双星的总质量如何表示?
[思维深化]
1.
若在双星模型中,图中L、m1、m2、G为已知量,双星运动的周期如何表示?
2.
若双星运动的周期为T,双星之间的距离为L,G已知,双星的总质量如何表示?
[思维深化]
1.
若在双星模型中,图中L、m1、m2、G为已知量,双星运动的周期如何表示?
2.
若双星运动的周期为T,双星之间的距离为L,G已知,双星的总质量如何表示?
[思维深化]
2.
三星模型
①三颗星位于同一直线上,两颗环绕星围绕中央星在同一半径为R的圆形轨道上运行(如图甲所示).
②三颗质量均为m的星体位于等边三角形的三个顶点上(如图乙所示)
.
m
m
m
r
2.
三星模型
①三颗星位于同一直线上,两颗环绕星围绕中央星在同一半径为R的圆形轨道上运行(如图甲所示).
②三颗质量均为m的星体位于等边三角形的三个顶点上(如图乙所示)
.
m
m
m
r
2.
三星模型
①三颗星位于同一直线上,两颗环绕星围绕中央星在同一半径为R的圆形轨道上运行(如图甲所示).
②三颗质量均为m的星体位于等边三角形的三个顶点上(如图乙所示)
.
m
m
m
r
2.
三星模型
①三颗星位于同一直线上,两颗环绕星围绕中央星在同一半径为R的圆形轨道上运行(如图甲所示).
②三颗质量均为m的星体位于等边三角形的三个顶点上(如图乙所示)
.
m
m
m
r
3.
四星模型
(1)如图所示,四颗质量相等的行星位于正方形的四个顶点上,沿外接于正方形的圆轨道做匀速圆周运动,
3.
四星模型
(1)如图所示,四颗质量相等的行星位于正方形的四个顶点上,沿外接于正方形的圆轨道做匀速圆周运动,
四颗行星转动的方向相同,周期、角速度、线速度的大小相等。
3.
四星模型
(1)如图所示,四颗质量相等的行星位于正方形的四个顶点上,沿外接于正方形的圆轨道做匀速圆周运动,
四颗行星转动的方向相同,周期、角速度、线速度的大小相等。
(2)如图所示:三颗质量相等的行星位于正三角形的三个顶点,另一颗恒星位于正三角形的中心O点,三颗行星以O点为圆心。绕正三角形的外接圆做匀速圆周运动。
(2)如图所示:三颗质量相等的行星位于正三角形的三个顶点,另一颗恒星位于正三角形的中心O点,三颗行星以O点为圆心。绕正三角形的外接圆做匀速圆周运动。
外围三颗行星转动的方向相同,周期、角速度、线速度的大小均相等。
(2)如图所示:三颗质量相等的行星位于正三角形的三个顶点,另一颗恒星位于正三角形的中心O点,三颗行星以O点为圆心。绕正三角形的外接圆做匀速圆周运动。
外围三颗行星转动的方向相同,周期、角速度、线速度的大小均相等。
【例题】(多选)如图所示,甲、乙、丙是位于同一直线上的离其他恒星较远的三颗恒星,甲、丙围绕乙在半径为R的圆轨道上运行。若三颗星质量均为M,万有引力常量为G,则(
)
B.
乙星所受合外力为
D.
甲星和丙星的角速度相同
A.
甲星所受合外力为
C.
甲星和丙星的线速度相同
【例题】(多选)如图所示,甲、乙、丙是位于同一直线上的离其他恒星较远的三颗恒星,甲、丙围绕乙在半径为R的圆轨道上运行。若三颗星质量均为M,万有引力常量为G,则(
)
B.
乙星所受合外力为
D.
甲星和丙星的角速度相同
A.
甲星所受合外力为
C.
甲星和丙星的线速度相同
ACD
题4.
我们的银河系的恒星中大约四分之一是双星.某双星由质量不等的星体S1和S2构成,两星在相互之间的万有引力作用下绕两者连线上某一定点C做匀速圆周运动.由天文观察测得其运动周期为T,S1到C点的距离为r1,S1和S2的距离为r,已知引力常量为G.由此可求出S2的质量为(
)
B.
A.
C.
D.
题4.
我们的银河系的恒星中大约四分之一是双星.某双星由质量不等的星体S1和S2构成,两星在相互之间的万有引力作用下绕两者连线上某一定点C做匀速圆周运动.由天文观察测得其运动周期为T,S1到C点的距离为r1,S1和S2的距离为r,已知引力常量为G.由此可求出S2的质量为(
)
B.
A.
C.
D.
D
地面上抛出的物体,由于受到地球引力的作用,最终都要落回到地面。
1.月球也要受到地球引力的作用,为什么月亮不会落到地面上来?
一、牛顿关于卫星的设想
地面上抛出的物体,由于受到地球引力的作用,最终都要落回到地面。
1.月球也要受到地球引力的作用,为什么月亮不会落到地面上来?
由于月球在绕地球沿近似圆周的轨道运转,此时月球受到的地球引力,用来充当绕地球运转的向心力,故月球不会落到地面上来。
一、牛顿关于卫星的设想
平抛运动演示
让物体做平抛运动初速度逐渐增大
一、牛顿关于卫星的设想
从高山上水平抛出物体,速度越大,落地点离山脚越远。如果没有空气阻力,当速度足够大时,物体就永远不会落到地面上来,它将围绕地球旋转,成为一颗永远绕地球运动的人造卫星。
一、牛顿关于卫星的设想
牛顿人造卫星原理图
从高山上水平抛出物体,速度越大,落地点离山脚越远。如果没有空气阻力,当速度足够大时,物体就永远不会落到地面上来,它将围绕地球旋转,成为一颗永远绕地球运动的人造卫星。
一、牛顿关于卫星的设想
思考
以多大的速度将物体抛出,它才会成为绕地球表面运动的卫星?
二、宇宙速度
思考
以多大的速度将物体抛出,它才会成为绕地球表面运动的卫星?
方法一:万有引力提供物体作圆周运动的向心力
二、宇宙速度
思考
以多大的速度将物体抛出,它才会成为绕地球表面运动的卫星?
方法一:万有引力提供物体作圆周运动的向心力
方法二:地表附近,重力近似等于万有引力
二、宇宙速度
g=9.8m/s2,R=6400km,代入数据得:
由此可见:v=7.9km/s,这就是物体在地面附近绕地球做匀速圆周运动所必须具备的最小发射速度,称为:第一宇宙速度
二、宇宙速度
由此可见:v=7.9km/s,这就是物体在地面附近绕地球做匀速圆周运动所必须具备的最小发射速度,称为:第一宇宙速度
说明:
(1)
如果卫星的速度小于第一宇宙速度,卫星将落到地面而不能绕地球运转;
二、宇宙速度
由此可见:v=7.9km/s,这就是物体在地面附近绕地球做匀速圆周运动所必须具备的最小发射速度,称为:第一宇宙速度
说明:
(1)
如果卫星的速度小于第一宇宙速度,卫星将落到地面而不能绕地球运转;
(2)等于这个速度,卫星刚好能在地球表面附近作匀速圆周运动;
二、宇宙速度
P
v=7.9km/s
11.2>v>7.9
v>11.2km/s
探究:若卫星的发射速度大于7.9km/s
,会怎样呢?
1.
第一宇宙速度:
v1=7.9km/s
地球
11.2km/s>v>7.9km/s
2.
第二宇宙速度:
v2=11.2km/s
v3=16.7km/s
3.
第三宇宙速度:
→人造行星
→人造恒星
→人造卫星
例1.
某人在一星球上以速率
v
竖直上抛一物体,经时间
t
后,物体以速率
v
落回手中。已知该星球的半径为
R
,求该星球上的第一宇宙速度。
例1.
某人在一星球上以速率
v
竖直上抛一物体,经时间
t
后,物体以速率
v
落回手中。已知该星球的半径为
R
,求该星球上的第一宇宙速度。
解析:星球表面的重力加速度:
该星球表面的第一宇宙速度为
第一宇宙速度为卫星在其表面附近做匀速圆周运动的线速度卫星的重力提供向心力,则:
思考:将各种卫星绕地球运动都近似看成匀速圆周运动,你能推出卫星环绕速度、角速度、周期、向心加速度与轨道半径的关系吗?
1
2
4
3
人造卫星运行的动力学方程
三、人造地球卫星运行的规律
地球
思考:对于绕地球运动的人造卫星:
(1)离地面越高,向心力越_____.
(2)离地面越高,线速度越_____.
(3)离地面越高,周期越_____.
(4)离地面越高,角速度越____.
三、人造地球卫星运行的规律
地球
思考:对于绕地球运动的人造卫星:
(1)离地面越高,向心力越_____.
(2)离地面越高,线速度越_____.
(3)离地面越高,周期越_____.
(4)离地面越高,角速度越____.
小
三、人造地球卫星运行的规律
地球
思考:对于绕地球运动的人造卫星:
(1)离地面越高,向心力越_____.
(2)离地面越高,线速度越_____.
(3)离地面越高,周期越_____.
(4)离地面越高,角速度越____.
小
小
三、人造地球卫星运行的规律
地球
思考:对于绕地球运动的人造卫星:
(1)离地面越高,向心力越_____.
(2)离地面越高,线速度越_____.
(3)离地面越高,周期越_____.
(4)离地面越高,角速度越____.
小
大
小
三、人造地球卫星运行的规律
地球
思考:对于绕地球运动的人造卫星:
(1)离地面越高,向心力越_____.
(2)离地面越高,线速度越_____.
(3)离地面越高,周期越_____.
(4)离地面越高,角速度越____.
小
大
小
小
三、人造地球卫星运行的规律
地球
思考:对于绕地球运动的人造卫星:
(1)离地面越高,向心力越_____.
(2)离地面越高,线速度越_____.
(3)离地面越高,周期越_____.
(4)离地面越高,角速度越____.
小
大
小
小
第一宇宙速度是发射卫星的最小发射速度,也是卫星绕地球做圆周运动的最大运行速度.
三、人造地球卫星运行的规律
例2.
探测器绕月球做匀速圆周运动,变轨后在周期较小的轨道上仍做匀速圆周运动,则变轨后与变轨前相比(
)
A.
轨道半径变小
B.
向心加速度变小
C.
线速度变小
D.
角速度变小
例2.
探测器绕月球做匀速圆周运动,变轨后在周期较小的轨道上仍做匀速圆周运动,则变轨后与变轨前相比(
)
A.
轨道半径变小
B.
向心加速度变小
C.
线速度变小
D.
角速度变小
A
例3.
如图所示,a、b、c是地球大气层外圆形轨道上运行的三颗人造地球卫星,a、b质量相同,且小于c的质量,则(
)
A.
b所需向心力最大
B.
b、c周期相等,且大于a周期
C.
b、c向心加速度相等,且大于a的向心加速度
D.
b、c的线速度大小相等,且小于a的线速度
a
c
b
地球
例3.
如图所示,a、b、c是地球大气层外圆形轨道上运行的三颗人造地球卫星,a、b质量相同,且小于c的质量,则(
)
A.
b所需向心力最大
B.
b、c周期相等,且大于a周期
C.
b、c向心加速度相等,且大于a的向心加速度
D.
b、c的线速度大小相等,且小于a的线速度
BD
a
c
b
地球
各种各样的卫星……
四、人造地球卫星
赤道轨道
四、人造地球卫星
赤道轨道
极地轨道
四、人造地球卫星
赤道轨道
其它轨道
极地轨道
四、人造地球卫星
所有卫星都在以地心为圆心的圆或椭圆轨道上
三类人造地球卫星轨道:
①赤道轨道,卫星轨道在赤道平面,卫星始终处于赤道上方
②极地轨道,卫星轨道平面与赤道平面垂直,卫星通过两极上空
③一般轨道,卫星轨道和赤道成一定角度。
人造地球卫星的运行轨道
地球同步卫星
相对于地面静止的,和地球具有相同周期的卫星,T=24h,因为地球同步卫星主要用于通信等方面,故地球同步卫星又叫通信卫星
F1
F2
F3
h
若同步卫星离地面高度h
特点:
特点:
⑴定周期:T=24h=86400s
特点:
⑴定周期:T=24h=86400s
⑵定点:相对于地面静止。
特点:
⑴定周期:T=24h=86400s
⑵定点:相对于地面静止。
⑶定轨道:同步卫星轨道必须在赤道上空
特点:
⑴定周期:T=24h=86400s
⑵定点:相对于地面静止。
⑶定轨道:同步卫星轨道必须在赤道上空
⑷定高度:h=36000km
特点:
⑴定周期:T=24h=86400s
⑵定点:相对于地面静止。
⑶定轨道:同步卫星轨道必须在赤道上空
⑷定高度:h=36000km
⑸定速度:由于同步卫星高度确定,其轨道半径即确定,因此线速度、角速度大小均不变
特点:
⑴定周期:T=24h=86400s
⑵定点:相对于地面静止。
⑶定轨道:同步卫星轨道必须在赤道上空
⑷定高度:h=36000km
⑸定速度:由于同步卫星高度确定,其轨道半径即确定,因此线速度、角速度大小均不变
⑹定加速度:由于同步卫星高度确定,其轨道半径即确定,因此向心加速度大小也不变
四、人造地球卫星
同步卫星
近地卫星
月球
近地卫星、同步卫星、月球三者比较
h=3.8×108m
r≈3.8×108m
v=1km/s
T=27天
同步卫星
近地卫星
月球
近地卫星、同步卫星、月球三者比较
h=3.6×107m
r=4.2×107m
v=3km/s
T=24h
h=3.8×108m
r≈3.8×108m
v=1km/s
T=27天
同步卫星
近地卫星
月球
近地卫星、同步卫星、月球三者比较
h=3.6×107m
r=4.2×107m
v=3km/s
T=24h
h=3.8×108m
r≈3.8×108m
v=1km/s
T=27天
h≈0
r=6.4×106m
v=7.9km/s
T=84分钟
同步卫星
近地卫星
月球
近地卫星、同步卫星、月球三者比较
变轨
思考:人造卫星在低轨道上运行,要想让其在高轨道上运行,应采取什么措施?
v
F引
F引<F向
F引>F向
卫星变轨原理
M
m
A点速度—内小外大(在A点看轨迹)
在A点万有引力相同
A
v
F引
1
2
R
卫星在圆轨道运行速度V1
v2
θ>900
减小
卫星变轨原理
v3
F引
L
卫星变轨原理
使卫星进入更高轨道做圆周运动
v3
v4
·
1.
卫星在二轨道相切点
万有引力相同
速度—内小外大(切点看轨迹)
2.
卫星在椭圆轨道运行
近地点---速度大,动能大
远地点---速度小,动能小
1.
如图所示,发射同步卫星时,先将卫星发射至近地圆轨道1,然后经点火使其沿椭圆轨道2运行;最后再次点火将其送入同步圆轨道3。轨道1、2相切于P点,2、3相切于Q点。当卫星分别在1、2、3上正常运行时,以下说法正确的是(
)
A.
在轨道3上的速率大于1上的速率
B.
在轨道3上的角速度小于1上的角速度
C.
在轨道2上经过Q点时的速率等于
在轨道3上经过Q点时的速率
D.
在轨道1上经过P点时的加速度等于
在轨道2上经过P点时的加速度
Q
P
2
·
3
1
1.
如图所示,发射同步卫星时,先将卫星发射至近地圆轨道1,然后经点火使其沿椭圆轨道2运行;最后再次点火将其送入同步圆轨道3。轨道1、2相切于P点,2、3相切于Q点。当卫星分别在1、2、3上正常运行时,以下说法正确的是(
)
A.
在轨道3上的速率大于1上的速率
B.
在轨道3上的角速度小于1上的角速度
C.
在轨道2上经过Q点时的速率等于
在轨道3上经过Q点时的速率
D.
在轨道1上经过P点时的加速度等于
在轨道2上经过P点时的加速度
Q
P
2
·
3
1
BD
空间站实际上就是一个载有人的人造卫星,那么,地球上的人如何登到空间站,空间站上的人又如何返回地面?这些活动都需要通过宇宙飞船来完成,这就存在一个宇宙飞船与空间站对接的问题。
思考:能否把宇宙飞船先发射到空间站的同一轨道上,再通过加速去追上空间站实现对接呢?
宇宙飞船与空间站对接问题
空间站
飞船
对接方法:
飞船首先在比空间站低的轨道运行,当运行到适当位置时,再加速运行到一个椭圆轨道。
空间站
飞船
对接方法:
飞船首先在比空间站低的轨道运行,当运行到适当位置时,再加速运行到一个椭圆轨道。
通过控制轨道使飞船跟空间站恰好同时运行到两轨道的相切点,此时飞船适当减速,便可实现对接,如图示。
空间站
飞船
对接方法:
2.
宇宙飞船和轨道空间站在同一轨道上运动,若飞船想与前面的空间站对接,飞船为了追上轨道空间站,可采取的方法是:
(
)
A.
飞船加速直到追上
B.
飞船从原轨道减速至一个较低轨道,再加速追上空间站,完成对接
C.
飞船加速至一个较高轨道再减速追上空间站,完成对接
D.
无论飞船采取何种措施,均不能与空间站对接
2.
宇宙飞船和轨道空间站在同一轨道上运动,若飞船想与前面的空间站对接,飞船为了追上轨道空间站,可采取的方法是:
(
)
A.
飞船加速直到追上
B.
飞船从原轨道减速至一个较低轨道,再加速追上空间站,完成对接
C.
飞船加速至一个较高轨道再减速追上空间站,完成对接
D.
无论飞船采取何种措施,均不能与空间站对接
B
二、人造卫星的超重和失重
二、人造卫星的超重和失重
1.
发射和回收阶段
二、人造卫星的超重和失重
1.
发射和回收阶段
发射
加速上升
超重
二、人造卫星的超重和失重
1.
发射和回收阶段
发射
加速上升
超重
回收
减速下降
超重
二、人造卫星的超重和失重
1.
发射和回收阶段
发射
加速上升
超重
回收
减速下降
超重
2.
沿圆轨道正常运行
二、人造卫星的超重和失重
1.
发射和回收阶段
发射
加速上升
超重
回收
减速下降
超重
2.
沿圆轨道正常运行
只受重力
a
=
g
完全失重
二、人造卫星的超重和失重
1.
发射和回收阶段
发射
加速上升
超重
回收
减速下降
超重
2.
沿圆轨道正常运行
只受重力
a
=
g
完全失重
与重力有关的现象全部消失
二、人造卫星的超重和失重
1.
发射和回收阶段
发射
加速上升
超重
回收
减速下降
超重
2.
沿圆轨道正常运行
只受重力
a
=
g
完全失重
与重力有关的现象全部消失
天平
弹簧秤测重力
液体压强计
三、多星系统
1.
双星问题
(1)定义:绕公共圆心转动的两个星体组成的系统,我们称之为双星系统,如图所示.
(2)特点:
①各自所需的向心力由彼此间的万有引力相互提供,即
(2)特点:
①各自所需的向心力由彼此间的万有引力相互提供,即
②两颗星的周期及角速度都相同,即
T1=T2,ω1=ω2
(2)特点:
①各自所需的向心力由彼此间的万有引力相互提供,即
②两颗星的周期及角速度都相同,即
T1=T2,ω1=ω2
③两颗星的半径与它们之间的距离关系为:
r1+r2=L
1.
若在双星模型中,图中L、m1、m2、G为已知量,双星运动的周期如何表示?
2.
若双星运动的周期为T,双星之间的距离为L,G已知,双星的总质量如何表示?
[思维深化]
1.
若在双星模型中,图中L、m1、m2、G为已知量,双星运动的周期如何表示?
2.
若双星运动的周期为T,双星之间的距离为L,G已知,双星的总质量如何表示?
[思维深化]
1.
若在双星模型中,图中L、m1、m2、G为已知量,双星运动的周期如何表示?
2.
若双星运动的周期为T,双星之间的距离为L,G已知,双星的总质量如何表示?
[思维深化]
2.
三星模型
①三颗星位于同一直线上,两颗环绕星围绕中央星在同一半径为R的圆形轨道上运行(如图甲所示).
②三颗质量均为m的星体位于等边三角形的三个顶点上(如图乙所示)
.
m
m
m
r
2.
三星模型
①三颗星位于同一直线上,两颗环绕星围绕中央星在同一半径为R的圆形轨道上运行(如图甲所示).
②三颗质量均为m的星体位于等边三角形的三个顶点上(如图乙所示)
.
m
m
m
r
2.
三星模型
①三颗星位于同一直线上,两颗环绕星围绕中央星在同一半径为R的圆形轨道上运行(如图甲所示).
②三颗质量均为m的星体位于等边三角形的三个顶点上(如图乙所示)
.
m
m
m
r
2.
三星模型
①三颗星位于同一直线上,两颗环绕星围绕中央星在同一半径为R的圆形轨道上运行(如图甲所示).
②三颗质量均为m的星体位于等边三角形的三个顶点上(如图乙所示)
.
m
m
m
r
3.
四星模型
(1)如图所示,四颗质量相等的行星位于正方形的四个顶点上,沿外接于正方形的圆轨道做匀速圆周运动,
3.
四星模型
(1)如图所示,四颗质量相等的行星位于正方形的四个顶点上,沿外接于正方形的圆轨道做匀速圆周运动,
四颗行星转动的方向相同,周期、角速度、线速度的大小相等。
3.
四星模型
(1)如图所示,四颗质量相等的行星位于正方形的四个顶点上,沿外接于正方形的圆轨道做匀速圆周运动,
四颗行星转动的方向相同,周期、角速度、线速度的大小相等。
(2)如图所示:三颗质量相等的行星位于正三角形的三个顶点,另一颗恒星位于正三角形的中心O点,三颗行星以O点为圆心。绕正三角形的外接圆做匀速圆周运动。
(2)如图所示:三颗质量相等的行星位于正三角形的三个顶点,另一颗恒星位于正三角形的中心O点,三颗行星以O点为圆心。绕正三角形的外接圆做匀速圆周运动。
外围三颗行星转动的方向相同,周期、角速度、线速度的大小均相等。
(2)如图所示:三颗质量相等的行星位于正三角形的三个顶点,另一颗恒星位于正三角形的中心O点,三颗行星以O点为圆心。绕正三角形的外接圆做匀速圆周运动。
外围三颗行星转动的方向相同,周期、角速度、线速度的大小均相等。
【例题】(多选)如图所示,甲、乙、丙是位于同一直线上的离其他恒星较远的三颗恒星,甲、丙围绕乙在半径为R的圆轨道上运行。若三颗星质量均为M,万有引力常量为G,则(
)
B.
乙星所受合外力为
D.
甲星和丙星的角速度相同
A.
甲星所受合外力为
C.
甲星和丙星的线速度相同
【例题】(多选)如图所示,甲、乙、丙是位于同一直线上的离其他恒星较远的三颗恒星,甲、丙围绕乙在半径为R的圆轨道上运行。若三颗星质量均为M,万有引力常量为G,则(
)
B.
乙星所受合外力为
D.
甲星和丙星的角速度相同
A.
甲星所受合外力为
C.
甲星和丙星的线速度相同
ACD
题4.
我们的银河系的恒星中大约四分之一是双星.某双星由质量不等的星体S1和S2构成,两星在相互之间的万有引力作用下绕两者连线上某一定点C做匀速圆周运动.由天文观察测得其运动周期为T,S1到C点的距离为r1,S1和S2的距离为r,已知引力常量为G.由此可求出S2的质量为(
)
B.
A.
C.
D.
题4.
我们的银河系的恒星中大约四分之一是双星.某双星由质量不等的星体S1和S2构成,两星在相互之间的万有引力作用下绕两者连线上某一定点C做匀速圆周运动.由天文观察测得其运动周期为T,S1到C点的距离为r1,S1和S2的距离为r,已知引力常量为G.由此可求出S2的质量为(
)
B.
A.
C.
D.
D
