多边形的内角和
图片预览



文档简介
(共39张PPT)
人教版数学教材七年级下
7.3多边形及其内角和
(1)节日彩旗
(4)景点掠影
(3)墙砖
(2)地砖
(5)蜜蜂窝表面
欣赏图片:
(6)钟面边缘
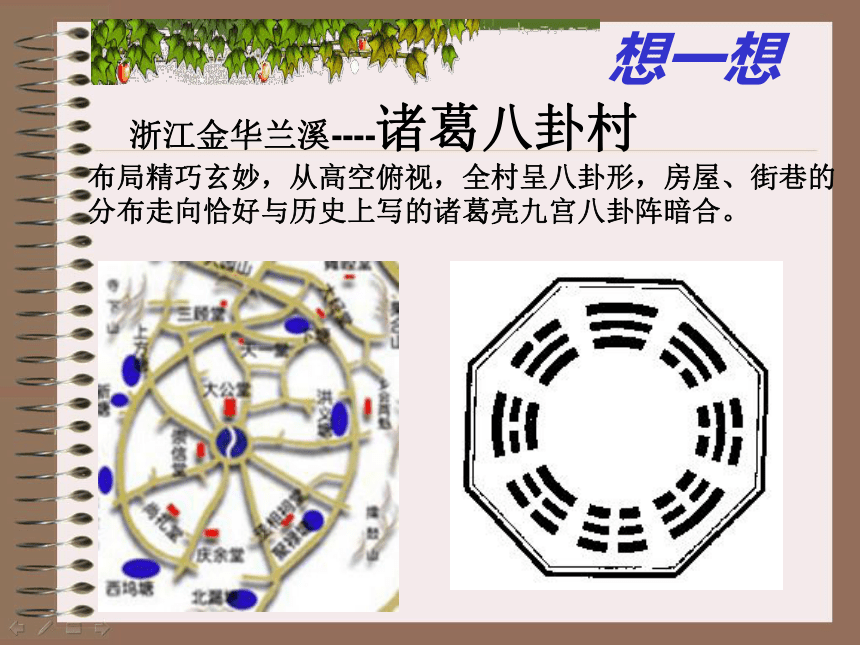
浙江金华兰溪----诸葛八卦村
布局精巧玄妙,从高空俯视,全村呈八卦形,房屋、街巷的
分布走向恰好与历史上写的诸葛亮九宫八卦阵暗合。
想一想
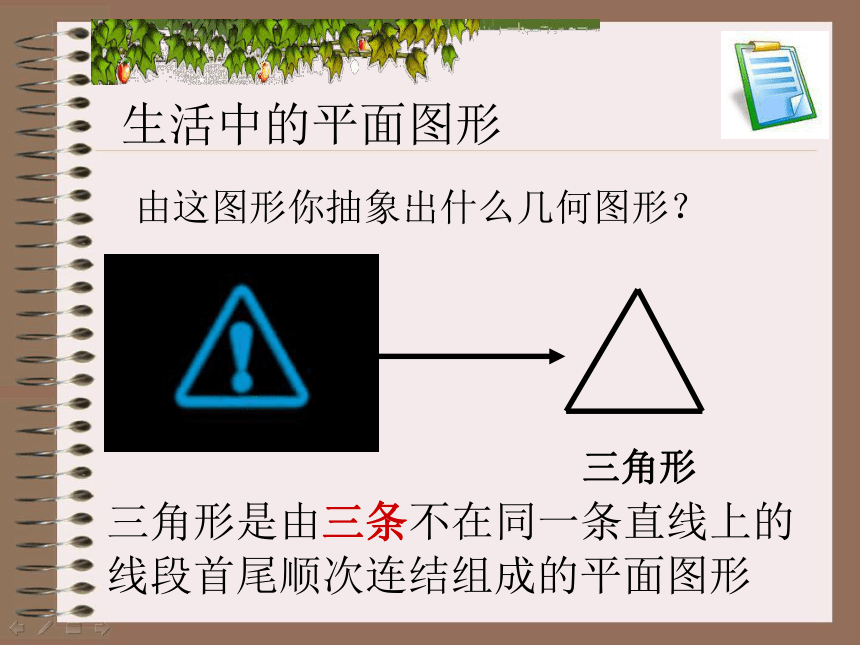
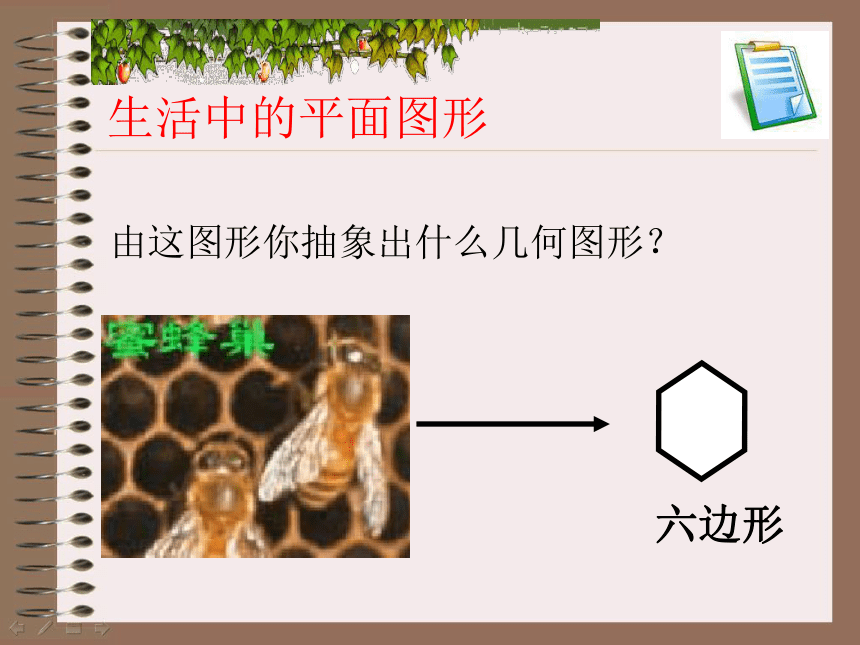
生活中的平面图形
由这图形你抽象出什么几何图形?
三角形
三角形是由三条不在同一条直线上的线段首尾顺次连结组成的平面图形
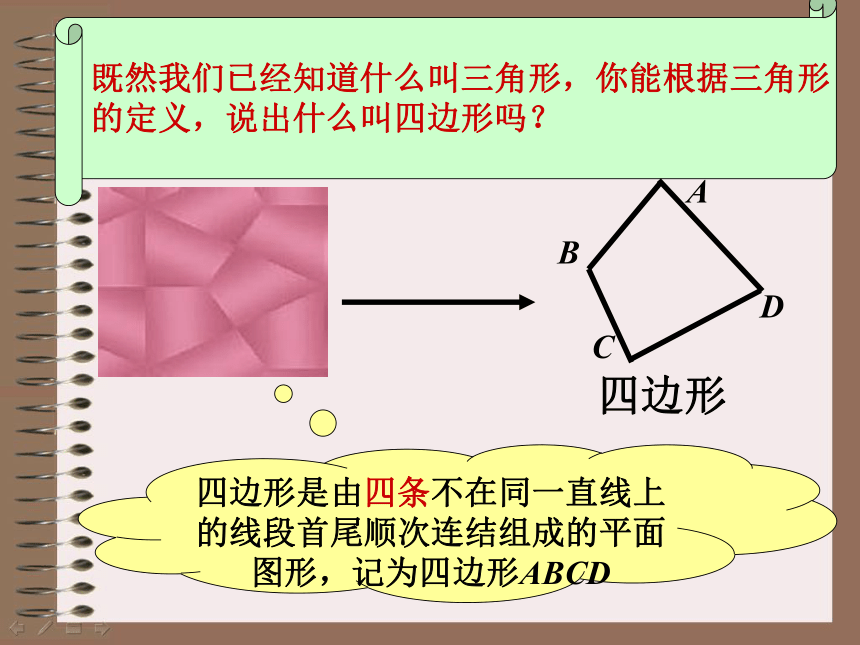
既然我们已经知道什么叫三角形,你能根据三角形
的定义,说出什么叫四边形吗?
四边形是由四条不在同一直线上的线段首尾顺次连结组成的平面图形,记为四边形ABCD
四边形
A
D
B
C
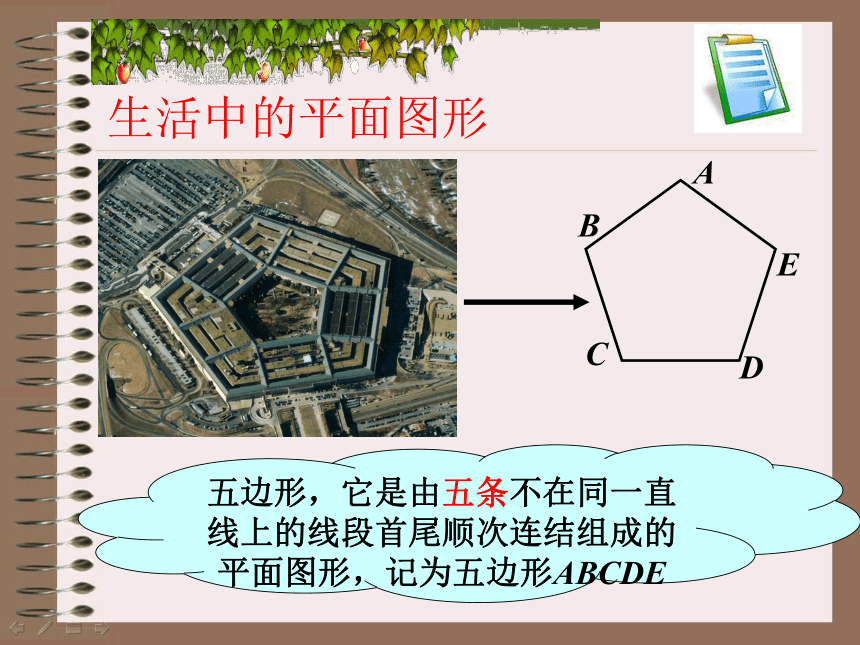
五边形,它是由五条不在同一直线上的线段首尾顺次连结组成的平面图形,记为五边形ABCDE
A
E
D
C
B
生活中的平面图形
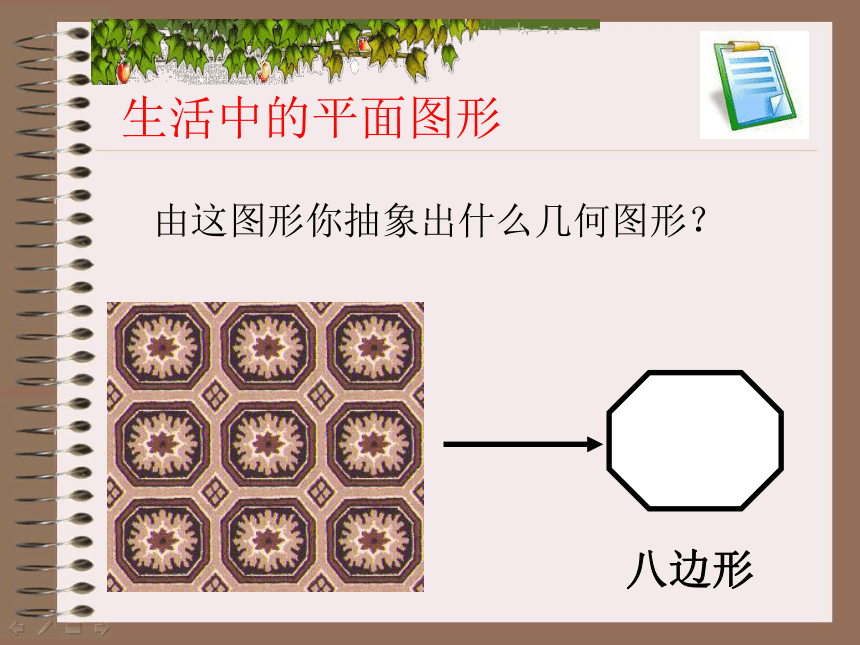
生活中的平面图形
由这图形你抽象出什么几何图形?
六边形
生活中的平面图形
由这图形你抽象出什么几何图形?
八边形
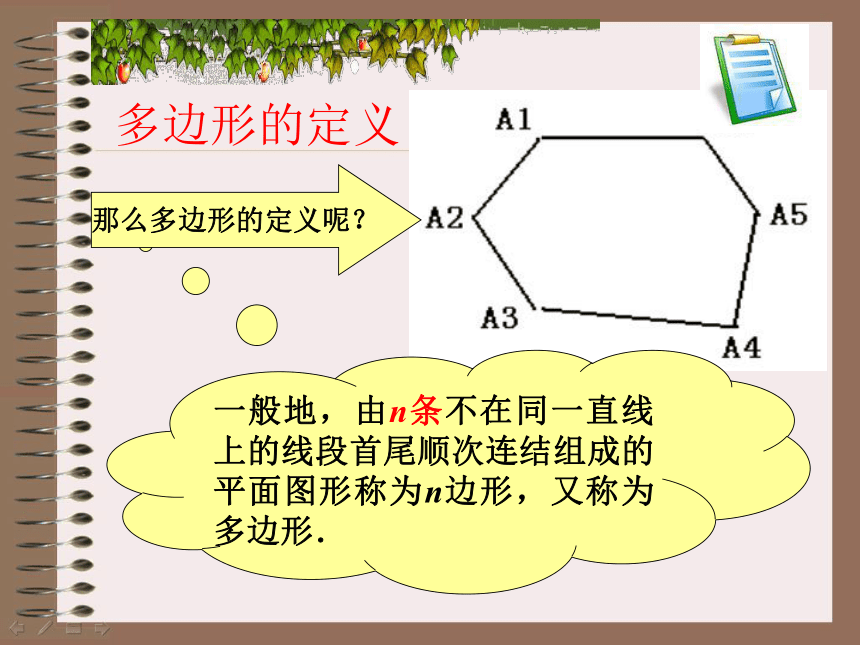
一般地,由n条不在同一直线上的线段首尾顺次连结组成的平面图形称为n边形,又称为多边形.
那么多边形的定义呢?
多边形的定义
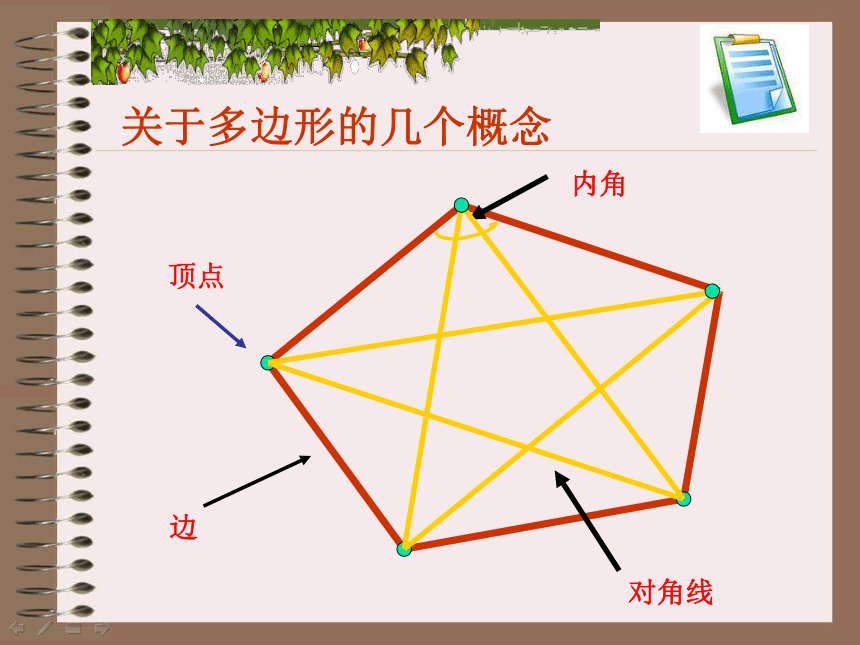
关于多边形的几个概念
顶点
内角
边
对角线
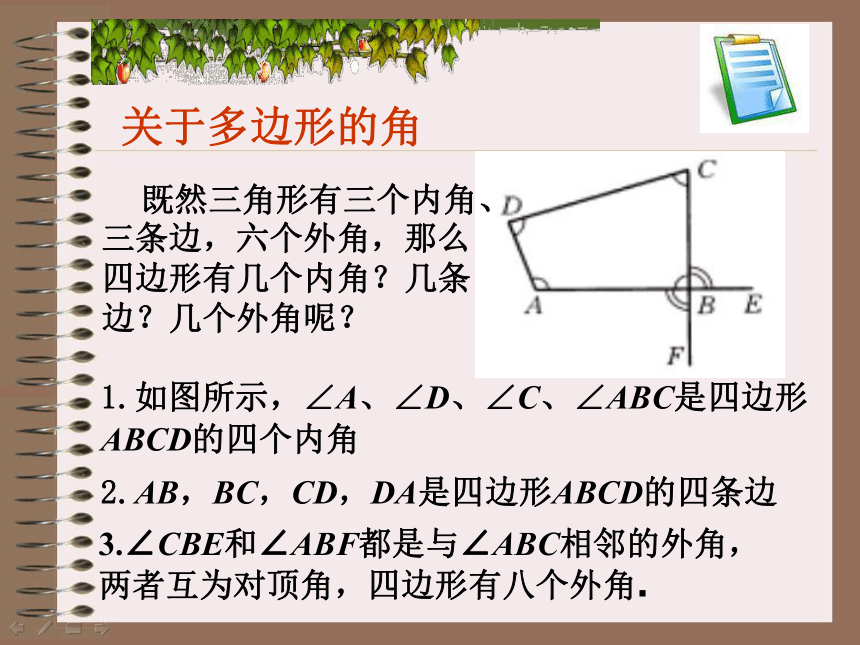
1.如图所示,∠A、∠D、∠C、∠ABC是四边形ABCD的四个内角
3.∠CBE和∠ABF都是与∠ABC相邻的外角,
两者互为对顶角,四边形有八个外角.
既然三角形有三个内角、三条边,六个外角,那么四边形有几个内角?几条边?几个外角呢?
2.AB,BC,CD,DA是四边形ABCD的四条边
关于多边形的角
那么五边形有几个内角?几条边?几个外角呢?
那么六边形有几个内角?几条边?几个外角呢?
那么n边形有几个内角?几条边?几个外角呢?
n边形有n个内角,n条边,2n个外角
六边形有6个内角,6条边,12个外角
五边形有5个内角,5条边,10个外角
关于多边形的角
请大家细心地填一填,多边形的内角,边,外角三者的关系表,你能发现什么规律?
3
3
4
4
5
5
6
6
7
7
n
n
6
8
10
12
14
2n
下面所示的图形也是多边形,但不在我们现在研究的范围内
注 意
我们现在研究的是如右图所示的多边形,也就是所谓的凸多边形
有什么不同?
凹多边形
凸多边形
三角形如果三条边都相等,三个角也都相等,那么这样的三角形就叫做正三角形。
如果多边形各边都相等,各个角也都相等,那么这样的多边形就叫做正多边形.如正三角形、正四边形(正方形)、正五边形等等 .
正三角形
正四边形
正五边形
正六边形
正八边形
(或正三边形)
(或正四边形)
关于特殊的多边形
连结多边形不相邻的两个顶点的线段叫做多边形的对角线.
线段AC是四边形ABCD的一条对角线;
多边形的对角线常用虚线表示。
关于多边形的对角线
四边形ABCD共有2条对角线。
请大家思考:五边形ABCDE共有几条对角线呢?
共有5条对角线
关于多边形的对角线
六边形ABCDEF共有几条对角线呢?
共有9条对角线
有没有什么
规律呢?
四边形从一个顶点出发,能引出__条对角线
五边形从一个顶点出发,能引出__条对角线
六边形从一个顶点出发,能引出__条对角线
n边形从一个顶点出发,能引出____条对角线
……
1
2
3
n-3
四边形从一个顶点出发,能引出1条对角线
它把四边形分成了几个三角形?
五边形从一个顶点出发,能引出2条对角线?
它把五边形分成了几个三角形?
关于多边形的对角线
n边形从一个顶点出发,能引出(n-3)条对角线?
它把n边形分成了几个三角形?
A
C
B
如图,三角形ABC的内角和是多少度?
探索多边形的内角和
探索多边形的内角和
A
B
C
D
四边形的内角和是多少度?
图中有几个三角形?
探索多边形的内角和
A
B
D
C
E
五边形的内角和是多少度?
图中有几个三角形?
探索多边形的内角和
A
B
D
C
F
E
六边形的内角和是多少度?
图中有几个三角形?
2、我们也可以利用下列不同的方法分割多边形,得到n边形的内角和公式
p
p
p
试一试
图 形 边数 过一顶点的
三角形个数 内角和的度数
4
5
6
7
n
2 个
3 个
4 个
5 个
n-2 个
3 ╳ 180°= 540°
2 ╳ 180°= 360°
4 ╳ 180°= 720°
5 ╳ 180°= 900°
(n-2 )╳ 180°
n边形内角和等于
议一议
(n-2)× 180°
1、(抢答) 8边形的内角和等于多少度? 十边形呢?
(8-2) ×
180°= 1080°
(10-2) ×
180°=
1440°
随堂练习
一 问题的指出
大家清晨跑步吗?小明就有每天坚持跑步的好习惯,他怎样跑步呢?右图就是小明清晨沿一个五边形广场周围的小跑,按逆时针方向跑步的效果图. 请你观察并思考如下几个问题:
. (3)在上图中,你能求出1+∠2+∠3+∠4+∠5的大小吗?你是怎样得到的?
(3)由上述知道:∠1,∠2,∠3,∠4,∠5分别是小明从一条街道转到下一条街道时,身体转过的角,通过实验可知:如果他跑一圈,身体转过的角度是360°,因此得
∠1+∠2+∠3+∠4+∠5=360°
想一想:
还有什么方法可以求出1+∠2+∠3+∠4+∠5的大小吗?
1 演示实验的方法
法(1):让五个人做为五边形的顶点,围成
一个五边形,由另一位表演小明跑步,跑
完一圈后,他的身体转过的角度之和是 .因此得
360°
法(2):在一张纸上画一个类似的五边形广场,将∠1、∠2、∠3、∠4、∠5剪来,顶点拼在一起恰好组成一个周角,因此
∠1+∠2+∠3+∠4+∠5=
360°
∠1+∠2+∠3+∠4+∠5=360°
解:∵∠1+∠6=180°,∠2+∠7=180°,
∠3+∠8=180°,∠4+∠9=180°,
∠5+∠10=180°
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8+∠9+∠10
=180*5=900°
而∠6+∠7+∠8+∠9+∠10 =540°
∴ ∠1+∠2+∠3+∠4+∠5 =360°
3 推理证明法:
多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角(exterior angle)
在每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和.
一般地,在多边形的任一顶点处按顺(逆)时针方向可作外角,n边形有n个外角.
新课:
分别求出下列多边形的外角和的度数.
360°
360°
360°
360°
360°
探索:
如果广场的形状是六边形、八边形,那么还有类似的结论吗?
推论:任意多边形的外 角和等于360 。
类比前边的做法,你能归纳出n 边形的外角和是多少吗?
∵ n边形的每一个外角与它相邻的内角的和是_____
∴ n边形的内角和加外角和等于 ________
∵ n 边形的内角和等于 ___________
A1
A2
A3
An
A4
证明:
180 ,
(n-2) 180 ,
∴ n 边形的外角和等于n 180 – (n-2) 180 =360 。
n 180 ,
[例1]一个多边形的内角和等于它的外角和的3倍,它是几边形?
解:设这个多边形是n边形,则它的内角和是(n-2)·180°,外角和等于360°,
所以:(n-2)·180=3×360
解得:n=8
答:这个多边形是八边形.
例题赏析
例2. 一个多边形当边数增加1时,它的内角和增加
多少度?
当边数增加1时,
解: 设多边形的边数为n,
因为它的内角和等于 (n-2) 180°,
(n+1-2) 180°- (n-2) 180°
=n 180°-180°-n 180°+360°
= 180°
内角和增加180°
内角和为(n+1-2) 180°,
天空的幸福是穿一身蓝
森林的幸福是披一身绿
阳光的幸福是如钻石般耀眼
致我亲爱的同学们
老师的幸福是因为认识了你们
愿你们努力进取,永不言败
人教版数学教材七年级下
7.3多边形及其内角和
(1)节日彩旗
(4)景点掠影
(3)墙砖
(2)地砖
(5)蜜蜂窝表面
欣赏图片:
(6)钟面边缘
浙江金华兰溪----诸葛八卦村
布局精巧玄妙,从高空俯视,全村呈八卦形,房屋、街巷的
分布走向恰好与历史上写的诸葛亮九宫八卦阵暗合。
想一想
生活中的平面图形
由这图形你抽象出什么几何图形?
三角形
三角形是由三条不在同一条直线上的线段首尾顺次连结组成的平面图形
既然我们已经知道什么叫三角形,你能根据三角形
的定义,说出什么叫四边形吗?
四边形是由四条不在同一直线上的线段首尾顺次连结组成的平面图形,记为四边形ABCD
四边形
A
D
B
C
五边形,它是由五条不在同一直线上的线段首尾顺次连结组成的平面图形,记为五边形ABCDE
A
E
D
C
B
生活中的平面图形
生活中的平面图形
由这图形你抽象出什么几何图形?
六边形
生活中的平面图形
由这图形你抽象出什么几何图形?
八边形
一般地,由n条不在同一直线上的线段首尾顺次连结组成的平面图形称为n边形,又称为多边形.
那么多边形的定义呢?
多边形的定义
关于多边形的几个概念
顶点
内角
边
对角线
1.如图所示,∠A、∠D、∠C、∠ABC是四边形ABCD的四个内角
3.∠CBE和∠ABF都是与∠ABC相邻的外角,
两者互为对顶角,四边形有八个外角.
既然三角形有三个内角、三条边,六个外角,那么四边形有几个内角?几条边?几个外角呢?
2.AB,BC,CD,DA是四边形ABCD的四条边
关于多边形的角
那么五边形有几个内角?几条边?几个外角呢?
那么六边形有几个内角?几条边?几个外角呢?
那么n边形有几个内角?几条边?几个外角呢?
n边形有n个内角,n条边,2n个外角
六边形有6个内角,6条边,12个外角
五边形有5个内角,5条边,10个外角
关于多边形的角
请大家细心地填一填,多边形的内角,边,外角三者的关系表,你能发现什么规律?
3
3
4
4
5
5
6
6
7
7
n
n
6
8
10
12
14
2n
下面所示的图形也是多边形,但不在我们现在研究的范围内
注 意
我们现在研究的是如右图所示的多边形,也就是所谓的凸多边形
有什么不同?
凹多边形
凸多边形
三角形如果三条边都相等,三个角也都相等,那么这样的三角形就叫做正三角形。
如果多边形各边都相等,各个角也都相等,那么这样的多边形就叫做正多边形.如正三角形、正四边形(正方形)、正五边形等等 .
正三角形
正四边形
正五边形
正六边形
正八边形
(或正三边形)
(或正四边形)
关于特殊的多边形
连结多边形不相邻的两个顶点的线段叫做多边形的对角线.
线段AC是四边形ABCD的一条对角线;
多边形的对角线常用虚线表示。
关于多边形的对角线
四边形ABCD共有2条对角线。
请大家思考:五边形ABCDE共有几条对角线呢?
共有5条对角线
关于多边形的对角线
六边形ABCDEF共有几条对角线呢?
共有9条对角线
有没有什么
规律呢?
四边形从一个顶点出发,能引出__条对角线
五边形从一个顶点出发,能引出__条对角线
六边形从一个顶点出发,能引出__条对角线
n边形从一个顶点出发,能引出____条对角线
……
1
2
3
n-3
四边形从一个顶点出发,能引出1条对角线
它把四边形分成了几个三角形?
五边形从一个顶点出发,能引出2条对角线?
它把五边形分成了几个三角形?
关于多边形的对角线
n边形从一个顶点出发,能引出(n-3)条对角线?
它把n边形分成了几个三角形?
A
C
B
如图,三角形ABC的内角和是多少度?
探索多边形的内角和
探索多边形的内角和
A
B
C
D
四边形的内角和是多少度?
图中有几个三角形?
探索多边形的内角和
A
B
D
C
E
五边形的内角和是多少度?
图中有几个三角形?
探索多边形的内角和
A
B
D
C
F
E
六边形的内角和是多少度?
图中有几个三角形?
2、我们也可以利用下列不同的方法分割多边形,得到n边形的内角和公式
p
p
p
试一试
图 形 边数 过一顶点的
三角形个数 内角和的度数
4
5
6
7
n
2 个
3 个
4 个
5 个
n-2 个
3 ╳ 180°= 540°
2 ╳ 180°= 360°
4 ╳ 180°= 720°
5 ╳ 180°= 900°
(n-2 )╳ 180°
n边形内角和等于
议一议
(n-2)× 180°
1、(抢答) 8边形的内角和等于多少度? 十边形呢?
(8-2) ×
180°= 1080°
(10-2) ×
180°=
1440°
随堂练习
一 问题的指出
大家清晨跑步吗?小明就有每天坚持跑步的好习惯,他怎样跑步呢?右图就是小明清晨沿一个五边形广场周围的小跑,按逆时针方向跑步的效果图. 请你观察并思考如下几个问题:
. (3)在上图中,你能求出1+∠2+∠3+∠4+∠5的大小吗?你是怎样得到的?
(3)由上述知道:∠1,∠2,∠3,∠4,∠5分别是小明从一条街道转到下一条街道时,身体转过的角,通过实验可知:如果他跑一圈,身体转过的角度是360°,因此得
∠1+∠2+∠3+∠4+∠5=360°
想一想:
还有什么方法可以求出1+∠2+∠3+∠4+∠5的大小吗?
1 演示实验的方法
法(1):让五个人做为五边形的顶点,围成
一个五边形,由另一位表演小明跑步,跑
完一圈后,他的身体转过的角度之和是 .因此得
360°
法(2):在一张纸上画一个类似的五边形广场,将∠1、∠2、∠3、∠4、∠5剪来,顶点拼在一起恰好组成一个周角,因此
∠1+∠2+∠3+∠4+∠5=
360°
∠1+∠2+∠3+∠4+∠5=360°
解:∵∠1+∠6=180°,∠2+∠7=180°,
∠3+∠8=180°,∠4+∠9=180°,
∠5+∠10=180°
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8+∠9+∠10
=180*5=900°
而∠6+∠7+∠8+∠9+∠10 =540°
∴ ∠1+∠2+∠3+∠4+∠5 =360°
3 推理证明法:
多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角(exterior angle)
在每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和.
一般地,在多边形的任一顶点处按顺(逆)时针方向可作外角,n边形有n个外角.
新课:
分别求出下列多边形的外角和的度数.
360°
360°
360°
360°
360°
探索:
如果广场的形状是六边形、八边形,那么还有类似的结论吗?
推论:任意多边形的外 角和等于360 。
类比前边的做法,你能归纳出n 边形的外角和是多少吗?
∵ n边形的每一个外角与它相邻的内角的和是_____
∴ n边形的内角和加外角和等于 ________
∵ n 边形的内角和等于 ___________
A1
A2
A3
An
A4
证明:
180 ,
(n-2) 180 ,
∴ n 边形的外角和等于n 180 – (n-2) 180 =360 。
n 180 ,
[例1]一个多边形的内角和等于它的外角和的3倍,它是几边形?
解:设这个多边形是n边形,则它的内角和是(n-2)·180°,外角和等于360°,
所以:(n-2)·180=3×360
解得:n=8
答:这个多边形是八边形.
例题赏析
例2. 一个多边形当边数增加1时,它的内角和增加
多少度?
当边数增加1时,
解: 设多边形的边数为n,
因为它的内角和等于 (n-2) 180°,
(n+1-2) 180°- (n-2) 180°
=n 180°-180°-n 180°+360°
= 180°
内角和增加180°
内角和为(n+1-2) 180°,
天空的幸福是穿一身蓝
森林的幸福是披一身绿
阳光的幸福是如钻石般耀眼
致我亲爱的同学们
老师的幸福是因为认识了你们
愿你们努力进取,永不言败
