三角形的内角和讲课用
图片预览






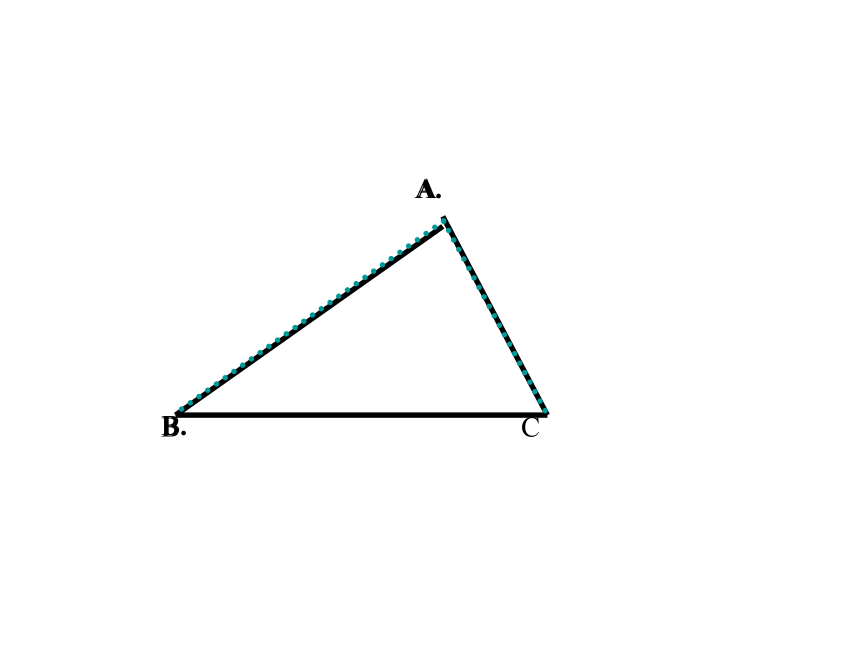
文档简介
(共35张PPT)
[1]有木条4根,长度分别为12㎝,10㎝,8㎝,4㎝,选其中三根组成三角形则选择的种数有( )
A.1 B.2 C.3 D.4
[2]三角形的两边长分别为2㎝和9㎝,第三边长为偶数。求第三边长。
三角形的内角和
新课
在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结。可是有一天,老二突然不高兴,发起脾气来,它指着老大说:“你凭什么度数最大,我也要和你一样大!”“不行啊!”老大说:“这是不可能的,否则,我们这个家就再也围不起来了……”“为什么?” 老二很纳闷。
同学们,你们知道其中的道理吗?
内角三兄弟之争
想一想
三角形的三个内角和是多少
有什么办法
可以验证呢
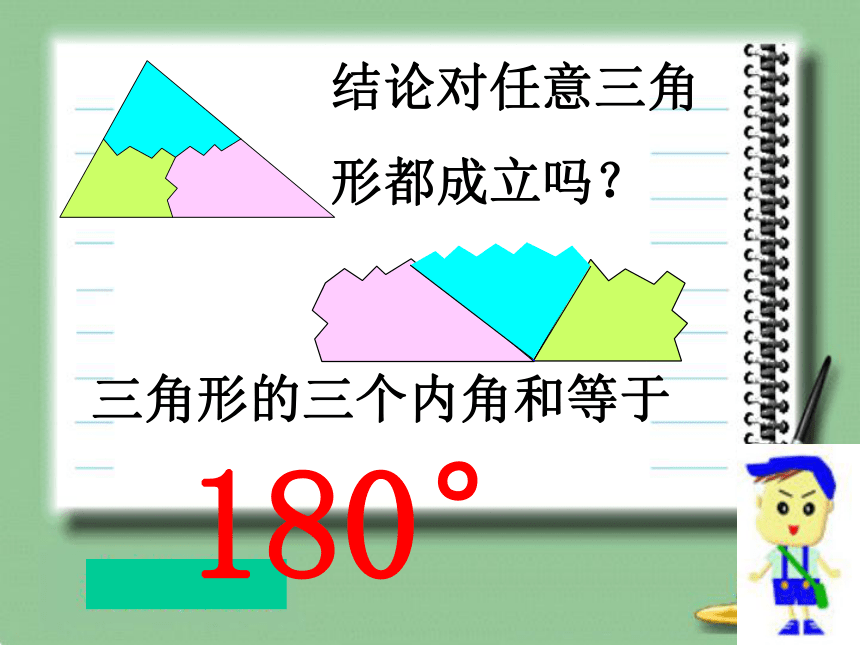
三角形的三个内角和等于 180°
结论对任意三角
形都成立吗?
想一想
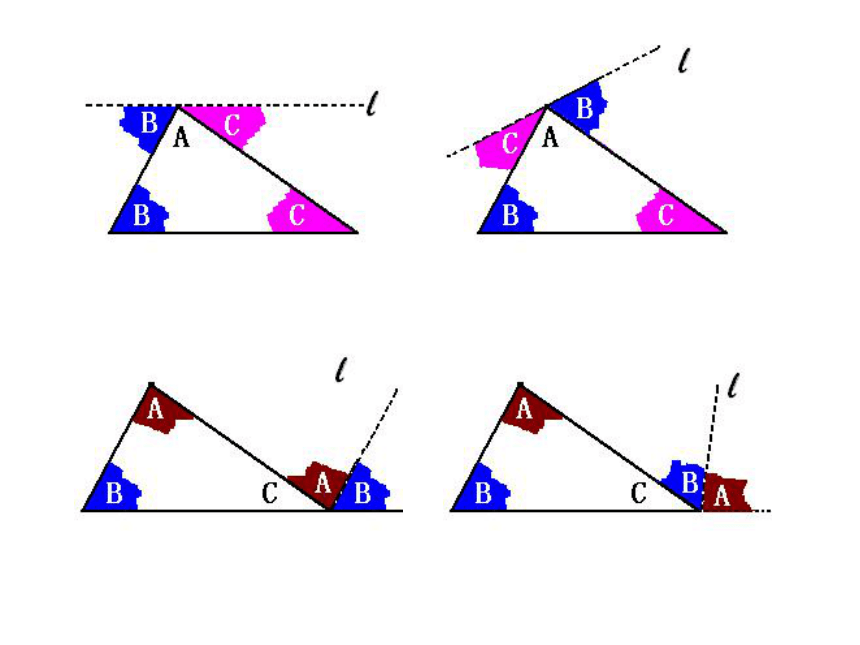
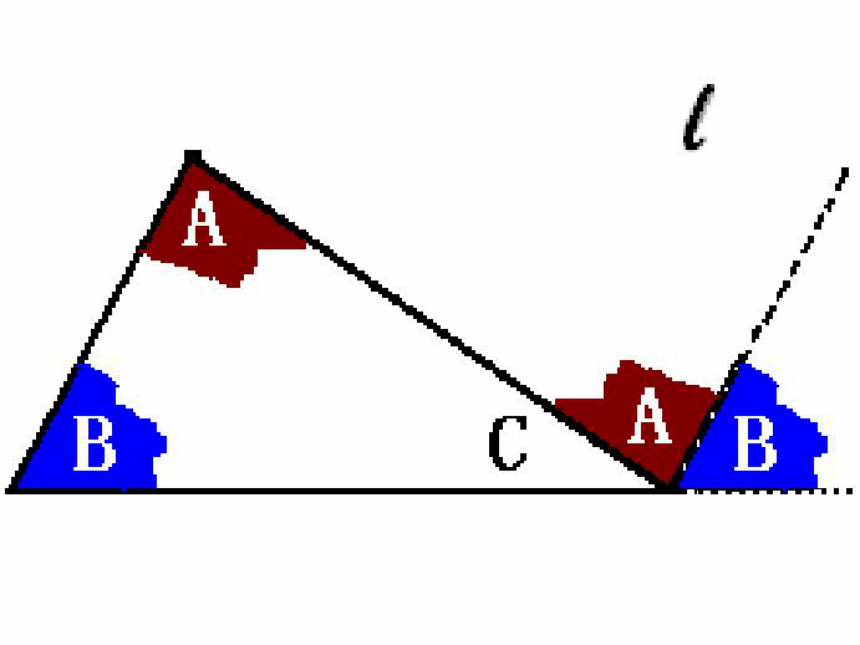
问题:有什么方法可以得到180°
1.平角的度数是180°
2.两直线平行,同旁内角的和是180°
从刚才拼角的过程你能想出证明的办法吗
A
B
C
A.
B.
A
B
C
A.
B.
A
B
C
A.
B.
A
B
C
A.
B.
E.
D.
A
B
C
A.
B.
A
证法1:
在△ABC的外部,以CA为一边,
CE为另一边作∠1=∠A,
E
延长BC到D,
于是CE∥BA
(内错角相等,两直线平行).
?
∴∠B=∠2
?
(两直线平行,同位角相等).
)
1
)
。
。
2
×
×
又∵∠1+∠2+∠ACB=180°
(平角的定义)
∴∠A+∠B+∠ACB=180°
?
?
(等量代换)
E
)
。
。
B
C
D
A
B
C
D
过C,作CE∥BA,
)
E
1
)
。
。
于是∠A=∠1
(两直线平行,内错角相等)
∠B=∠2
又∵∠1+∠2+∠ACB=180°
(平角的定义)
∴∠A+∠B+∠ACB=180°
2
×
×
?
?
(两直线平行,同位角相等)
?
?
(等量代换)
证法2:
作BC的延长线CD,
图形相同,
画法不同,
证明也不同.
想一想:利用此图该如何说明“三角形的内角和等于180°”?
证法3:
A
B
C
过A作EF∥BC,
E
F
∴∠B=∠BAE
(两直线平行,内错角相等)
∠C=∠CAF
(两直线平行,内错角相等)
又∵∠BAE+∠CAF+∠BAC=180°
∴∠B+∠C+∠BAC=180°
(平角的定义)
(等量代换)
证法4:
A
B
C
过A作AE∥BC,
E
∴∠B=∠BAE
(两直线平行,内错角相等)
∠EAB+∠BAC+∠C=180°
(两直线平行,同旁内角互补)
∴∠B+∠C+∠BAC=180°
(等量代换)
三角形的内角和等于180°
∠EAC+∠C=180°
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。
思路总结
为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.
三角形内角和定理:
三角形的内角和等于1800.
在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结。可是有一天,老二突然不高兴,发起脾气来,它指着老大说:“你凭什么度数最大,我也要和你一样大!”“不行啊!”老大说:“这是不可能的,否则,我们这个家就再也围不起来了……”“为什么?” 老二很纳闷。
同学们,你们知道其中的道理吗?
内角三兄弟之争
一个三角形中最多有几个直角?
一个三角形中最多有几个钝角?
一个三角形中最少有几个锐角?
检验一下自己吧!
(口答)下列各组角是同一个
三角形的内角吗?为什么?
(1)3°, 150°, 27°
(2)60°, 40°, 90°
(3)30°, 60°, 50°
(是 )
( 不是)
( 不是)
80°
X°
X°
你能求出图中X的值吗
1、 在△ABC中,∠A=80°,∠B=∠C , 求∠C的度数。
解:在△ABC中,
∠A+∠B+∠C=180°,∠A=80°
∴∠B+∠C=100°
∵∠B=∠C
∴∠B=∠C=500
2、已知三角形三个内角的度数之比为1:3:5,求这三个内角的度数。
解:设三个内角度数分别为:x、
3x、5x
列出方程 x+3x+5x=180
x=20
答:三个内角度数分别为
20°,60°,100°。
如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80 °方向,C岛在B岛的北偏西40 °方向。从C岛看A、B两岛的视角∠ACB是多少度?(图中AD∥BE)
拓展运用
北
东
西
南
F
M
N
北
.
A
D
北
.
C
B
.
E
50°
80°
40°
北
A
.
D
北
.
C
B
.
E
50°
80°
40°
解:
∵∠DAB=80°, ∠DAC=50°
∴∠CAB=30°
∵AD∥BE
∴∠DAB+∠EBA=180°
∴∠EBA=100°
∵ ∠ CBE=40°
∴ ∠ CBA=60°
∵ ∠ CBA+∠ACB+∠CBA=180°
∴ ∠ ACB=90°
(两直线平行,
同旁内角互补)
(三角形内角
和等于180)
3. 如图,一种滑翔伞是左右对称的四边形ABCD,其中∠A=150°,∠B=∠D=40°。求∠C的度数。
D
40 °
40 °
150°
A
B
C
1
2
如图,若AB∥CD,
则∠1、∠2与
∠C、∠D之间
有什么数量关
系?为什么?
∠1=∠C,∠2=∠D
∠1+∠2=∠C+∠D
如图,若AB不平行
于CD,则∠1、∠2
与∠C、∠D之间
的这些关系还成
立吗?为什么?
∠1+∠2=∠C+∠D
如图,若A、B分别在
DO、CO的延长线上,
则∠1、∠2与∠C、
∠D之间的关系还
成立吗?为什么?
∠1+∠2=∠C+∠D
1
2
A
B
C
D
O
1
2
A
B
C
D
O
1
2
A
B
C
D
O
如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一样的玻璃,那么最省事的办法是 ( )
(A)带①去 (B)带②去 (C)带③去 (D)带①和②去
C
2如图,求∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F 的度数.
A
B
C
D
M
E
N
F
O
1
3
分析:三个三角形9个
内角之和为5400
所以∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F
=5400-1800=3600
∠1+ ∠2+ ∠3=1800
2
拓展延伸:
5一块大型模板如图,设计要求BA与CD相交成30°角,DA与CB相交成20°角,怎样通过测量∠A、∠B、∠C、∠D的度数,来检验模板是否合格?
A
B
C
D
∠B+∠C=1500
∠D+∠C=1600
拓展延伸:
课堂小结
通过本堂课的学习,你有哪些收获?
[1]有木条4根,长度分别为12㎝,10㎝,8㎝,4㎝,选其中三根组成三角形则选择的种数有( )
A.1 B.2 C.3 D.4
[2]三角形的两边长分别为2㎝和9㎝,第三边长为偶数。求第三边长。
三角形的内角和
新课
在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结。可是有一天,老二突然不高兴,发起脾气来,它指着老大说:“你凭什么度数最大,我也要和你一样大!”“不行啊!”老大说:“这是不可能的,否则,我们这个家就再也围不起来了……”“为什么?” 老二很纳闷。
同学们,你们知道其中的道理吗?
内角三兄弟之争
想一想
三角形的三个内角和是多少
有什么办法
可以验证呢
三角形的三个内角和等于 180°
结论对任意三角
形都成立吗?
想一想
问题:有什么方法可以得到180°
1.平角的度数是180°
2.两直线平行,同旁内角的和是180°
从刚才拼角的过程你能想出证明的办法吗
A
B
C
A.
B.
A
B
C
A.
B.
A
B
C
A.
B.
A
B
C
A.
B.
E.
D.
A
B
C
A.
B.
A
证法1:
在△ABC的外部,以CA为一边,
CE为另一边作∠1=∠A,
E
延长BC到D,
于是CE∥BA
(内错角相等,两直线平行).
?
∴∠B=∠2
?
(两直线平行,同位角相等).
)
1
)
。
。
2
×
×
又∵∠1+∠2+∠ACB=180°
(平角的定义)
∴∠A+∠B+∠ACB=180°
?
?
(等量代换)
E
)
。
。
B
C
D
A
B
C
D
过C,作CE∥BA,
)
E
1
)
。
。
于是∠A=∠1
(两直线平行,内错角相等)
∠B=∠2
又∵∠1+∠2+∠ACB=180°
(平角的定义)
∴∠A+∠B+∠ACB=180°
2
×
×
?
?
(两直线平行,同位角相等)
?
?
(等量代换)
证法2:
作BC的延长线CD,
图形相同,
画法不同,
证明也不同.
想一想:利用此图该如何说明“三角形的内角和等于180°”?
证法3:
A
B
C
过A作EF∥BC,
E
F
∴∠B=∠BAE
(两直线平行,内错角相等)
∠C=∠CAF
(两直线平行,内错角相等)
又∵∠BAE+∠CAF+∠BAC=180°
∴∠B+∠C+∠BAC=180°
(平角的定义)
(等量代换)
证法4:
A
B
C
过A作AE∥BC,
E
∴∠B=∠BAE
(两直线平行,内错角相等)
∠EAB+∠BAC+∠C=180°
(两直线平行,同旁内角互补)
∴∠B+∠C+∠BAC=180°
(等量代换)
三角形的内角和等于180°
∠EAC+∠C=180°
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。
思路总结
为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.
三角形内角和定理:
三角形的内角和等于1800.
在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结。可是有一天,老二突然不高兴,发起脾气来,它指着老大说:“你凭什么度数最大,我也要和你一样大!”“不行啊!”老大说:“这是不可能的,否则,我们这个家就再也围不起来了……”“为什么?” 老二很纳闷。
同学们,你们知道其中的道理吗?
内角三兄弟之争
一个三角形中最多有几个直角?
一个三角形中最多有几个钝角?
一个三角形中最少有几个锐角?
检验一下自己吧!
(口答)下列各组角是同一个
三角形的内角吗?为什么?
(1)3°, 150°, 27°
(2)60°, 40°, 90°
(3)30°, 60°, 50°
(是 )
( 不是)
( 不是)
80°
X°
X°
你能求出图中X的值吗
1、 在△ABC中,∠A=80°,∠B=∠C , 求∠C的度数。
解:在△ABC中,
∠A+∠B+∠C=180°,∠A=80°
∴∠B+∠C=100°
∵∠B=∠C
∴∠B=∠C=500
2、已知三角形三个内角的度数之比为1:3:5,求这三个内角的度数。
解:设三个内角度数分别为:x、
3x、5x
列出方程 x+3x+5x=180
x=20
答:三个内角度数分别为
20°,60°,100°。
如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80 °方向,C岛在B岛的北偏西40 °方向。从C岛看A、B两岛的视角∠ACB是多少度?(图中AD∥BE)
拓展运用
北
东
西
南
F
M
N
北
.
A
D
北
.
C
B
.
E
50°
80°
40°
北
A
.
D
北
.
C
B
.
E
50°
80°
40°
解:
∵∠DAB=80°, ∠DAC=50°
∴∠CAB=30°
∵AD∥BE
∴∠DAB+∠EBA=180°
∴∠EBA=100°
∵ ∠ CBE=40°
∴ ∠ CBA=60°
∵ ∠ CBA+∠ACB+∠CBA=180°
∴ ∠ ACB=90°
(两直线平行,
同旁内角互补)
(三角形内角
和等于180)
3. 如图,一种滑翔伞是左右对称的四边形ABCD,其中∠A=150°,∠B=∠D=40°。求∠C的度数。
D
40 °
40 °
150°
A
B
C
1
2
如图,若AB∥CD,
则∠1、∠2与
∠C、∠D之间
有什么数量关
系?为什么?
∠1=∠C,∠2=∠D
∠1+∠2=∠C+∠D
如图,若AB不平行
于CD,则∠1、∠2
与∠C、∠D之间
的这些关系还成
立吗?为什么?
∠1+∠2=∠C+∠D
如图,若A、B分别在
DO、CO的延长线上,
则∠1、∠2与∠C、
∠D之间的关系还
成立吗?为什么?
∠1+∠2=∠C+∠D
1
2
A
B
C
D
O
1
2
A
B
C
D
O
1
2
A
B
C
D
O
如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一样的玻璃,那么最省事的办法是 ( )
(A)带①去 (B)带②去 (C)带③去 (D)带①和②去
C
2如图,求∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F 的度数.
A
B
C
D
M
E
N
F
O
1
3
分析:三个三角形9个
内角之和为5400
所以∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F
=5400-1800=3600
∠1+ ∠2+ ∠3=1800
2
拓展延伸:
5一块大型模板如图,设计要求BA与CD相交成30°角,DA与CB相交成20°角,怎样通过测量∠A、∠B、∠C、∠D的度数,来检验模板是否合格?
A
B
C
D
∠B+∠C=1500
∠D+∠C=1600
拓展延伸:
课堂小结
通过本堂课的学习,你有哪些收获?
